法拉第电磁感应定律(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。
法拉第电磁感应定律(简称法拉第定律)是电磁学中的一条定律,用于预测磁场如何与电路相互作用以产生电动势(emf)。这种现象被称为电磁感应,是变压器、电感器以及许多类型的电动机、发电机和螺线管的基本工作原理。[2][3]
麦克斯韦-法拉第方程(作为麦克斯韦方程组之一)描述了一个事实,即空间变化的(也可能是时间变化的,具体取决于磁场随时间的变化情况)电场总是伴随着时间变化的磁场,而法拉第定律则表明,当通过由导电回路包围的表面的磁通量随时间变化时,导电回路中会产生电动势(即单位电荷沿回路运动一圈时电磁作用所做的功)。
法拉第定律被发现后,其一个方面(变压器电动势)被表述为麦克斯韦-法拉第方程。法拉第定律的方程可以通过麦克斯韦-法拉第方程(描述变压器电动势)和洛伦兹力(描述运动电动势)推导而来。麦克斯韦-法拉第方程的积分形式仅描述变压器电动势,而法拉第定律的方程同时描述变压器电动势和运动电动势。
1. 历史
电磁感应现象分别由迈克尔·法拉第于 1831 年和约瑟夫·亨利于 1832 年独立发现。[4] 法拉第是第一个发表其实验结果的人。[5][6]
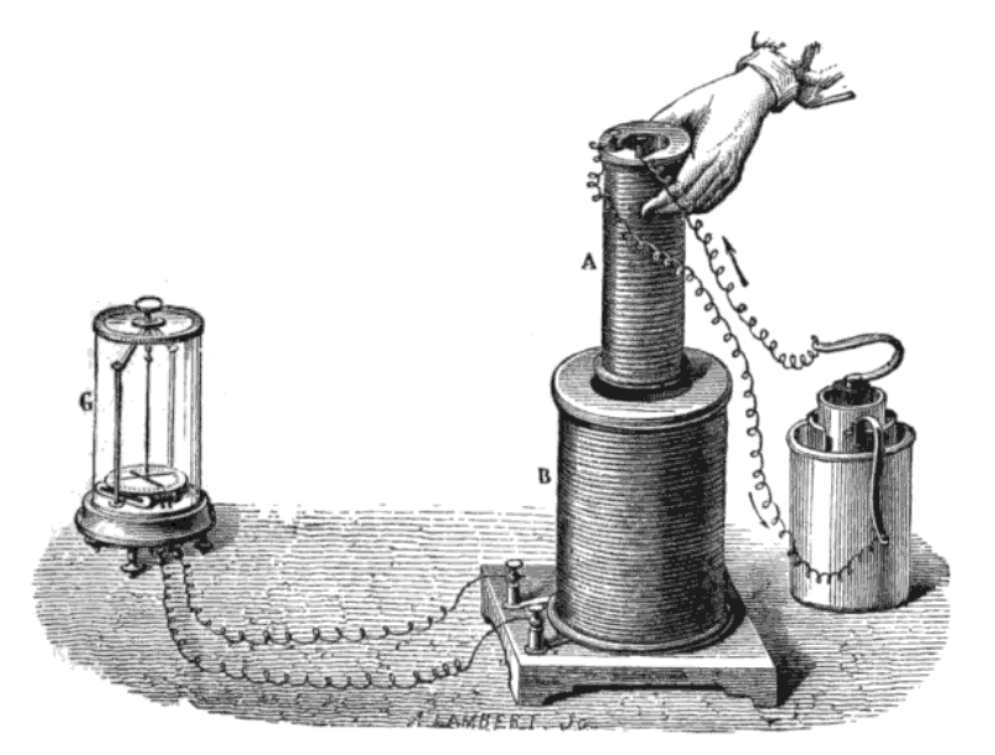
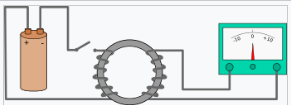
法拉第在 1831 年 8 月 29 日的笔记[8]中描述了一项电磁感应的实验演示(见图)[9],他将两根导线缠绕在铁环的两侧(类似于现代的环形变压器)。他对电磁铁新发现的特性进行了评估,并推测,当一侧的导线开始流过电流时,一种波动会通过铁环传播,并在另一侧引起某种电效应。确实,当他将左侧的导线连接或断开电池时,右侧导线连接的电流计的指针显示了瞬时电流(他称之为 “电波”)[10]: 182–183 。这种感应是由于电池连接或断开时产生的磁通量变化导致的。[7] 他的笔记还记录到,电池侧导线的圈数越少,电流计指针的扰动就越大。[8]
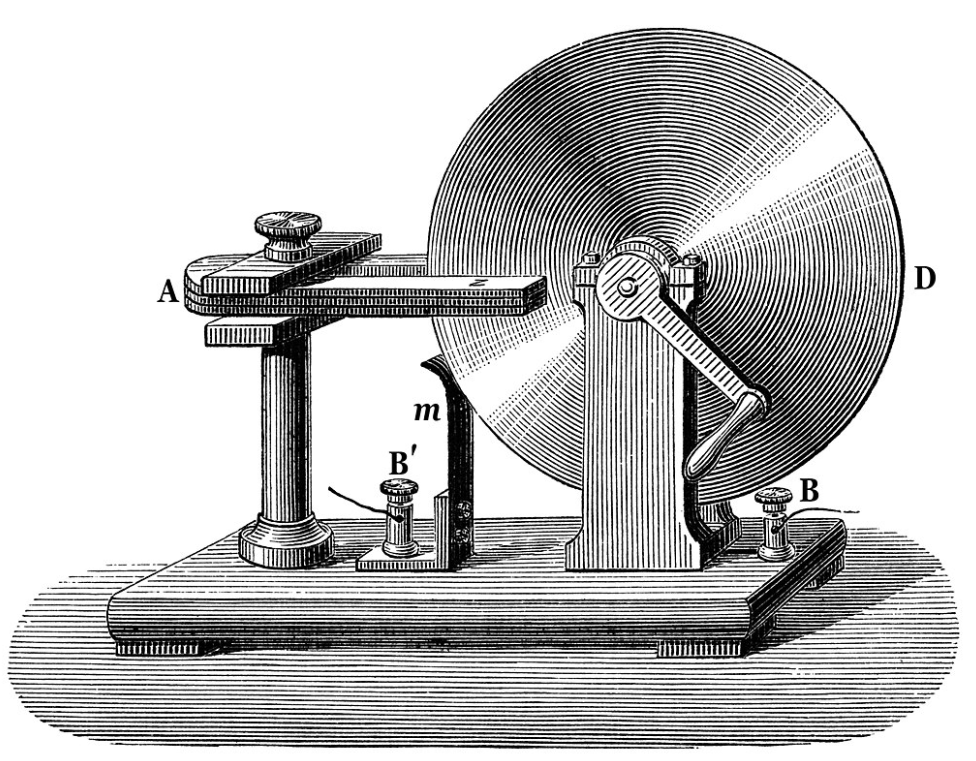
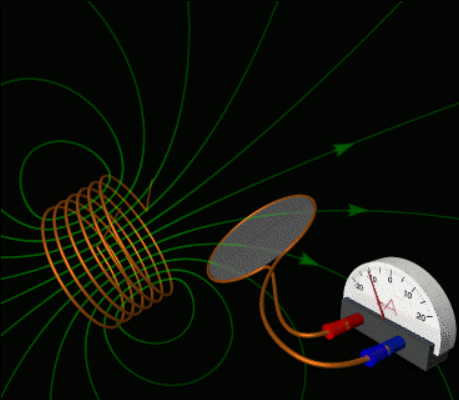
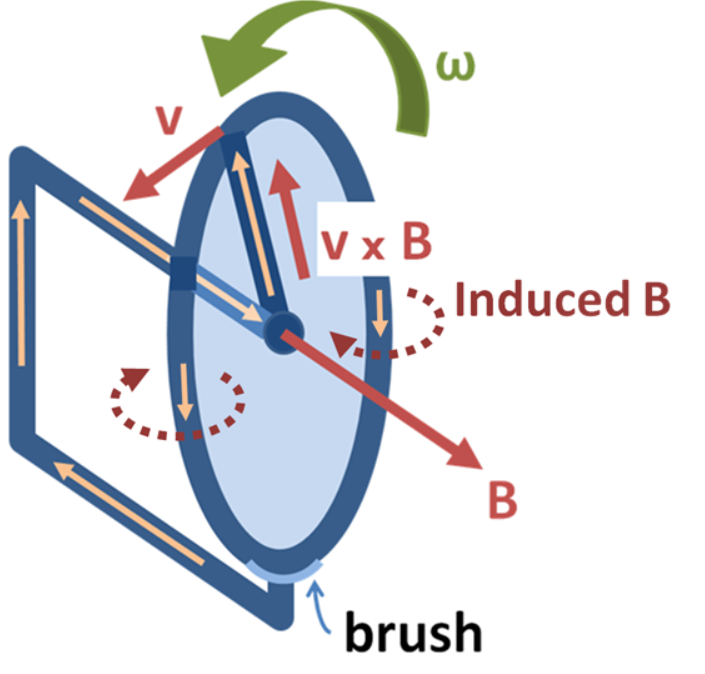
在两个月内,法拉第发现了几种其他形式的电磁感应。例如,他观察到,当他快速将一根条形磁铁插入或拉出线圈时,会产生瞬时电流;同时,他通过在条形磁铁附近旋转一个带有滑动电接触的铜盘(即 “法拉第圆盘”),生成了一个稳定的直流电流(DC)。[10]: 191–195
迈克尔·法拉第用他称为 “力线” 的概念解释了电磁感应。然而,当时的科学家普遍拒绝了他的理论观点,主要是因为这些观点没有用数学形式表述。[10]: 510 唯一的例外是詹姆斯·克拉克·麦克斯韦,他在 1861-1862 年以法拉第的思想为基础,建立了他的定量电磁理论。[10]: 510 [11][12] 在麦克斯韦的论文中,电磁感应的时间变化部分以微分方程的形式表达,奥利弗·亥维赛德将其称为 “法拉第定律”,尽管它与法拉第最初的定律版本不同,并未描述运动电动势(motional emf)。亥维赛德的版本(见下文麦克斯韦-法拉第方程)是如今被称为 “麦克斯韦方程组” 的方程形式之一。
**楞次定律**由埃米尔·楞次(Emil Lenz)于 1834 年提出,[13] 它描述了 “通过回路的磁通量”,并给出了由电磁感应产生的感应电动势和电流的方向(详见下文示例的扩展说明)。
根据阿尔伯特·爱因斯坦的说法,他的狭义相对论理论的大部分基础和发现来源于法拉第 1834 年提出的电磁感应定律。[14][15]
2. 法拉第定律
法拉第定律最广泛接受的版本表述为:
闭合路径上的电动势等于该路径所包围的磁通量随时间变化率的负值。[16][17]
数学表述
对于位于磁场中的一个导线环,磁通量 \( \Phi_B \) 定义为任何边界为给定导线环的表面 \( \Sigma \) 上的值。由于导线环可能在运动,我们用 \( \Sigma(t) \) 表示随时间变化的表面。磁通量通过以下表面积分定义: \[ \Phi_B = \iint_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d}\mathbf{A},~ \] 其中,\( \mathrm{d}\mathbf{A} \) 是运动表面 \( \Sigma(t) \) 上的面积矢量元素,\( \mathbf{B} \) 是磁场,\( \mathbf{B} \cdot \mathrm{d}\mathbf{A} \) 是磁通量通过 \( \mathrm{d}\mathbf{A} \) 的矢量点积。从视觉上来说,导线环中的磁通量与穿过环的磁场线的数量成正比。
当磁通量发生变化时(可能因为磁场 \( \mathbf{B} \) 发生变化,或者因为导线环运动或变形,或两者兼有),根据法拉第电磁感应定律,导线环中会产生电动势(emf)。电动势定义为单位电荷绕导线环一圈所能获得的能量。[18]: ch17 [19][20](尽管某些来源对定义有不同表述,这种定义方式是为与狭义相对论的方程保持一致。)等效地,这也是通过切断导线形成开路并用电压表连接两端测量到的电压。
法拉第定律表明,电动势(emf)也由磁通量的变化率给出: \[ \mathcal{E} = -\frac{\mathrm{d} \Phi_B}{\mathrm{d} t},~ \] 其中 \( \mathcal{E} \) 是电动势(emf),\( \Phi_B \) 是磁通量。
电动势的方向由楞次定律确定。
电流感应定律的数学形式由弗朗茨·恩斯特·诺依曼(Franz Ernst Neumann)于 1845 年确立。[21]
法拉第定律包含了关于变量的大小和方向之间关系的信息。然而,方向之间的关系并未明确表达,而是隐含在数学公式中。
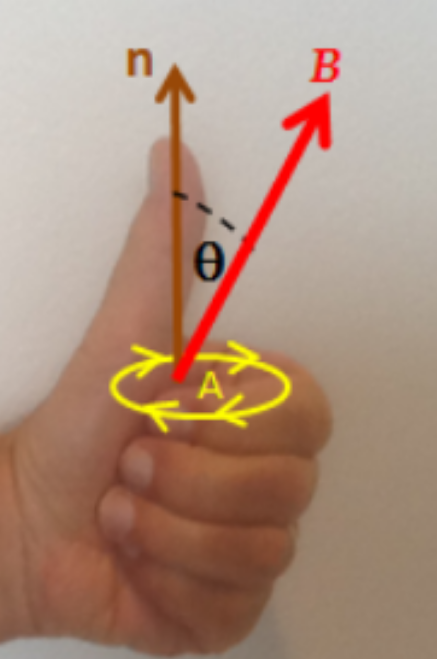
可以直接从法拉第定律确定电动势(emf)的方向,而无需借助楞次定律。以下的**左手法则**可以帮助确定方向:[22][23]
- 将左手的弯曲手指与导线环的方向对齐(黄色线)。
- 伸出大拇指。伸出的拇指表示法向量 \( \mathbf{n} \)(棕色)的方向,即环路所包围区域的法向量。
- 确定磁通量变化 \( \Delta \Phi_B \) 的符号。根据与法向量 \( \mathbf{n} \) 的关系,确定初始磁通量和最终磁通量(它们的差值即为 \( \Delta \Phi_B \))。
- 如果磁通量变化 \( \Delta \Phi_B \) 为正,弯曲手指的方向即为电动势的方向(黄色箭头)。
- 如果磁通量变化 \( \Delta \Phi_B \) 为负,电动势的方向与弯曲手指的方向相反(与黄色箭头相反)。
对于由 \( N \) 个相同线圈紧密绕成的导线圈,每个线圈具有相同的磁通量 \( \Phi_B \),法拉第电磁感应定律表述为:[24][25] \[ \mathcal{E} = -N \frac{\mathrm{d} \Phi_B}{\mathrm{d} t},~ \] 其中,\( N \) 是线圈的匝数,\( \Phi_B \) 是单个线圈的磁通量。
麦克斯韦–法拉第方程
麦克斯韦–法拉第方程表明,时间变化的磁场总是伴随着空间变化的(也可能是时间变化的)非保守电场,反之亦然。麦克斯韦–法拉第方程为: \[ \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}~ \] (以国际单位制表示),其中 \( \nabla \times \) 是旋度算符,\( \mathbf{E}(\mathbf{r}, t) \) 是电场,\( \mathbf{B}(\mathbf{r}, t) \) 是磁场。这些场通常是位置 \( \mathbf{r} \) 和时间 \( t \) 的函数。[26]
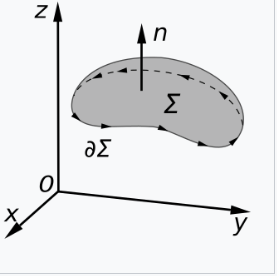
麦克斯韦–法拉第方程是麦克斯韦方程组中的四个方程之一,因此在经典电磁理论中具有基础性作用。通过开尔文–斯托克斯定理,该方程还可以以积分形式表示,[27] 从而重现法拉第定律: \[ \oint_{\partial \Sigma} \mathbf{E} \cdot \mathrm{d} \mathbf{l} = -\int_{\Sigma} \frac{\partial \mathbf{B}}{\partial t} \cdot \mathrm{d} \mathbf{A}~ \] 其中,如图所示,\( \Sigma \) 是由闭合曲线 \( \partial \Sigma \) 包围的一个表面,\( \mathrm{d}\mathbf{l} \) 是曲线 \( \partial \Sigma \) 上的微小矢量元素,\( \mathrm{d}\mathbf{A} \) 是表面 \( \Sigma \) 上的微小矢量元素,其方向垂直于该表面片段,大小为该表面微小片段的面积。
\(\mathrm{d}\mathbf{l}\) 和 \(\mathrm{d}\mathbf{A}\) 都存在符号的歧义。为了确定正确的符号,使用右手法则,如**开尔文–斯托克斯定理**文章中所述。对于平面表面 \(\Sigma\),曲线 \(\partial \Sigma\) 上的正路径元素 \(\mathrm{d}\mathbf{l}\) 根据右手法则定义:当右手拇指指向表面 \(\Sigma\) 的法向量 \(\mathbf{n}\) 时,手指所指的方向即为正路径方向。
围绕 \(\partial \Sigma\) 的线积分称为**环流**。[18]: ch3 环流为非零的电场 \(\mathbf{E}\) 的行为不同于由静电荷产生的电场。由电荷生成的电场 \(\mathbf{E}\) 可以表示为标量场的梯度,该标量场是泊松方程的解,其路径积分为零(详见梯度定理)。
此积分方程对空间中任何路径 \(\partial \Sigma\) 及以该路径为边界的任何表面 \(\Sigma\) 都成立。
如果表面 \(\Sigma\) 随时间不发生变化,该方程可以改写为: \[ \oint_{\partial \Sigma} \mathbf{E} \cdot \mathrm{d}\mathbf{l} = -\frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma} \mathbf{B} \cdot \mathrm{d}\mathbf{A}.~ \] 右侧的表面积分是通过 \(\Sigma\) 的磁通量 \(\Phi_B\) 的显式表达式。
由变化的磁通量感应产生的电矢量场(整体电场的旋量分量)在非相对论极限下可以通过以下体积分方程近似表示:[26]: 321 \[ \mathbf{E}_s(\mathbf{r}, t) \approx -\frac{1}{4\pi} \iiint_V \frac{\left( \frac{\partial \mathbf{B}(\mathbf{r}', t)}{\partial t} \right) \times (\mathbf{r} - \mathbf{r}')}{|\mathbf{r} - \mathbf{r}'|^3} \, d^3\mathbf{r}'.~ \]
3. 证明
麦克斯韦的四个方程(包括麦克斯韦–法拉第方程)以及洛伦兹力定律是推导经典电磁学中所有内容的充分基础。[18][19] 因此,可以以这些方程为起点 “证明” 法拉第定律。[28][29]
起点是空间中任意表面 \( \Sigma \)(可以移动或变形)的磁通量随时间的变化率: \[ \frac{\mathrm{d} \Phi_B}{\mathrm{d} t} = \frac{\mathrm{d}}{\mathrm{d} t} \int_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d} \mathbf{A}~ \] (由定义得出)。利用麦克斯韦–法拉第方程和一些矢量恒等式,可以对该全时间导数进行计算和简化;详细步骤见下方框中:
考虑通过一个可以移动或变形的闭合边界(回路)的磁通量的时间导数。该回路所包围的面积记为 \( \Sigma(t) \),则时间导数可以表示为: \[ \frac{\mathrm{d} \Phi_B}{\mathrm{d} t} = \frac{\mathrm{d}}{\mathrm{d} t} \int_{\Sigma(t)} \mathbf{B}(t) \cdot \mathrm{d} \mathbf{A}~ \] 积分随时间变化有两个原因:积分函数(被积函数)可能变化,或者积分区域可能变化。这两部分的变化是线性叠加的,因此: \[ \left. \frac{\mathrm{d} \Phi_B}{\mathrm{d} t} \right|_{t=t_0} = \left( \int_{\Sigma(t_0)} \left. \frac{\partial \mathbf{B}}{\partial t} \right|_{t=t_0} \cdot \mathrm{d} \mathbf{A} \right) + \left( \frac{\mathrm{d}}{\mathrm{d} t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d} \mathbf{A} \right)~ \] 其中,\( t_0 \) 是任意给定的固定时间。接下来将证明右侧的第一项对应于变压器电动势(transformer emf),第二项对应于运动电动势(motional emf),后者来源于导电回路在磁场中运动或变形时,对电荷载流子产生的洛伦兹力。
右侧的第一项可以通过麦克斯韦–法拉第方程的积分形式重新写为: \[ \int_{\Sigma(t_0)} \left. \frac{\partial \mathbf{B}}{\partial t} \right|_{t=t_0} \cdot \mathrm{d} \mathbf{A} = -\oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot \mathrm{d} \mathbf{l}~ \]
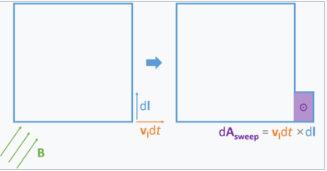
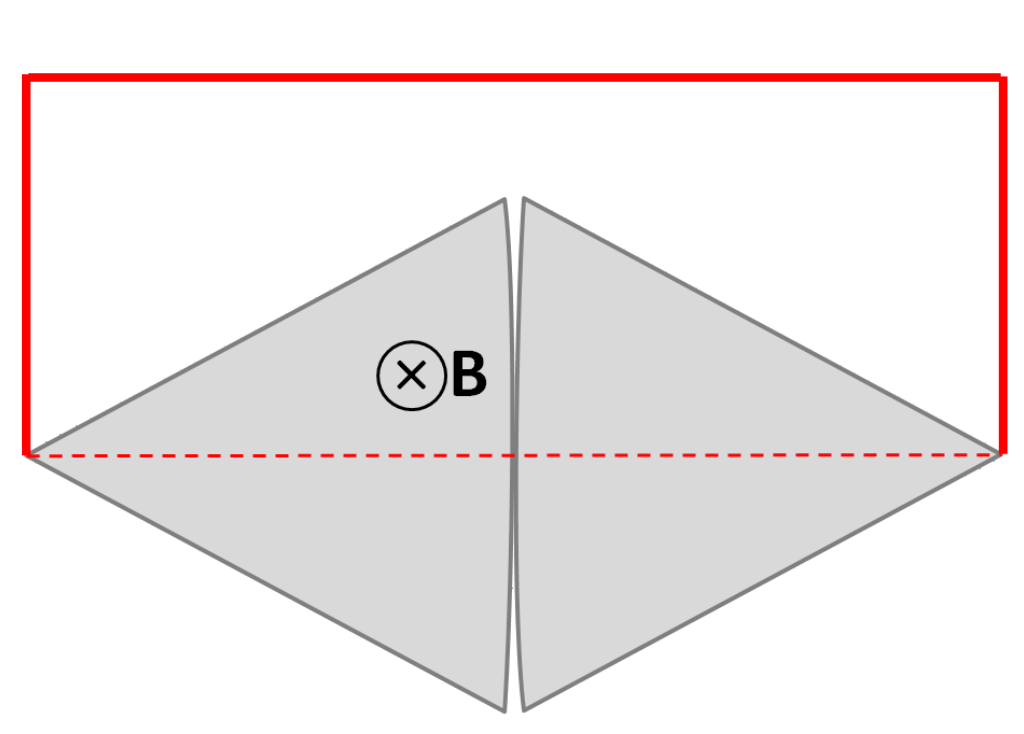
接下来分析上图的第二项: \[ \frac{\mathrm{d}}{\mathrm{d} t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d} \mathbf{A}~ \] 证明这一点比第一项略为复杂,更多细节和替代方法可参阅相关文献。[28][29][30] 当回路移动和/或变形时,它会扫过一个表面(参见右图)。当回路的一小部分 \( \mathrm{d}\mathbf{l} \) 以速度 \( \mathbf{v}_\mathbf{l} \) 在短时间 \( \mathrm{d}t \) 内移动时,它扫过的面积矢量为:\(\mathrm{d}\mathbf{A}_{\text{sweep}} = \mathbf{v}_\mathbf{l} \mathrm{d}t \times \mathrm{d}\mathbf{l}\)(注意,在上图中,该矢量指向屏幕外)。因此,由于回路的变形或移动,在时间 \( \mathrm{d}t \) 内通过回路的磁通量变化为: \[ \mathrm{d}\Phi_B = \int \mathbf{B} \cdot \mathrm{d}\mathbf{A}_{\text{sweep}} = \int \mathbf{B} \cdot (\mathbf{v}_\mathbf{l} \mathrm{d}t \times \mathrm{d}\mathbf{l}) = -\int \mathrm{d}t \, \mathrm{d}\mathbf{l} \cdot (\mathbf{v}_\mathbf{l} \times \mathbf{B})~ \] 这里使用了三重标量积的恒等式。因此: \[ \frac{\mathrm{d}}{\mathrm{d}t} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot \mathrm{d}\mathbf{A} = -\oint_{\partial \Sigma(t_0)} (\mathbf{v}_\mathbf{l}(t_0) \times \mathbf{B}(t_0)) \cdot \mathrm{d}\mathbf{l}~ \] 其中,\( \mathbf{v}_\mathbf{l} \) 是回路 \(\partial \Sigma\) 中某部分的速度。
将以上结果结合起来,可以得到: \[ \left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t} \right|_{t=t_0} = \left( -\oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot \mathrm{d}\mathbf{l} \right) + \left( -\oint_{\partial \Sigma(t_0)} (\mathbf{v}_\mathbf{l}(t_0) \times \mathbf{B}(t_0)) \cdot \mathrm{d}\mathbf{l} \right)~ \] 合并项后: \[ \left. \frac{\mathrm{d}\Phi_B}{\mathrm{d}t} \right|_{t=t_0} = -\oint_{\partial \Sigma(t_0)} \left( \mathbf{E}(t_0) + \mathbf{v}_\mathbf{l}(t_0) \times \mathbf{B}(t_0) \right) \cdot \mathrm{d}\mathbf{l}.~ \] 结果为: \[ \frac{\mathrm{d} \Phi_B}{\mathrm{d} t} = -\oint_{\partial \Sigma} \left( \mathbf{E} + \mathbf{v}_\mathbf{l} \times \mathbf{B} \right) \cdot \mathrm{d} \mathbf{l},~ \] 其中 \( \partial \Sigma \) 是表面 \( \Sigma \) 的边界(回路),\( \mathbf{v}_\mathbf{l} \) 是边界某部分的速度。
对于导电回路,电动势(emf)是单位电荷绕回路行进一圈时电磁力所做的功,这一功由洛伦兹力完成。因此,电动势表达为: \[ \mathcal{E} = \oint \left( \mathbf{E} + \mathbf{v} \times \mathbf{B} \right) \cdot \mathrm{d} \mathbf{l},~ \] 其中 \( \mathcal{E} \) 是电动势,\( \mathbf{v} \) 是单位电荷的速度。
在宏观视角下,对于回路中一段的电荷,速度 \( \mathbf{v} \) 平均由两个分量组成:一个是沿该段的电荷速度 \( \mathbf{v}_t \),另一个是该段的速度 \( \mathbf{v}_l \)(当回路被变形或移动时)。由于 \( \mathbf{v}_t \) 的方向与 \( \mathrm{d}\mathbf{l} \) 的方向相同,因此它不对电荷所做的功产生贡献。数学表达如下: \[ (\mathbf{v} \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l} = ((\mathbf{v}_t + \mathbf{v}_l) \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l} = (\mathbf{v}_t \times \mathbf{B} + \mathbf{v}_l \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l} = (\mathbf{v}_l \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l}~ \] 由于 \( (\mathbf{v}_t \times \mathbf{B}) \) 与 \( \mathrm{d}\mathbf{l} \) 垂直,且 \( \mathbf{v}_t \) 与 \( \mathrm{d}\mathbf{l} \) 方向相同。
因此,对于导电回路,电动势(emf)等于磁通量随时间的变化率,除了符号相反。由此得到法拉第定律的方程(针对导电回路): \[ \frac{\mathrm{d} \Phi_B}{\mathrm{d} t} = -\mathcal{E}~ \] 其中:\(\mathcal{E} = \oint \left( \mathbf{E} + \mathbf{v} \times \mathbf{B} \right) \cdot \mathrm{d}\mathbf{l}.\) 分解该积分:\(\oint \mathbf{E} \cdot \mathrm{d}\mathbf{l}\) 表示变压器电动势(由随时间变化的磁场引起),而 \(\oint (\mathbf{v} \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l} = \oint (\mathbf{v}_l \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l}\) 表示运动电动势(由回路在磁场中运动或变形时,磁洛伦兹力对电荷施加的作用所引起)。
4. 例外情况
很容易尝试将法拉第定律推广为以下陈述:如果 \(\partial\Sigma\) 是空间中任意闭合回路,那么通过 \(\Sigma\) 的磁通量的总时间导数等于沿 \(\partial\Sigma\) 的电动势。然而,这一陈述并非总是正确,其原因不仅仅在于当没有导体存在时,电动势在空旷空间中是未定义的。正如上一节所述,除非抽象曲线 \(\partial\Sigma\) 的速度与传导电流的材料的实际速度一致,否则法拉第定律并不一定适用。[31]
下文的两个示例说明了,当 \(\partial\Sigma\) 的运动与材料的运动分离时,往往会得到错误的结果。[18]
可以通过确保路径 \(\partial \Sigma\) 的运动速度与材料的速度相同来分析这些例子。[31] 或者,也可以通过将洛伦兹力定律与麦克斯韦-法拉第方程结合,总是正确地计算电动势:[18]: 第 17 章 [32] \[ \mathcal{E} = \int_{\partial \Sigma} (\mathbf{E} + \mathbf{v}_m \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l} = -\int_{\Sigma} \frac{\partial \mathbf{B}}{\partial t} \cdot \mathrm{d}\Sigma + \oint_{\partial \Sigma} (\mathbf{v}_m \times \mathbf{B}) \cdot \mathrm{d}\mathbf{l}~ \] 其中 “非常重要的是注意:(1) [\(\mathbf{v}_m\)] 是导体的速度……而不是路径元素 \(\mathrm{d}\mathbf{l}\) 的速度;以及 (2) 通常情况下,不能将对时间的偏导数移到积分号外,因为面积是时间的函数。”[32]
5. 法拉第定律与相对论
详见:运动磁铁与导体问题
两种现象
法拉第定律是一个单一的方程,但它描述了两种不同的现象:运动电动势:由磁力作用在移动导线上的运动电动势(参见洛伦兹力)。变压器电动势:由于变化的磁场引起的电场力产生的变压器电动势(由麦克斯韦-法拉第方程描述)。
詹姆斯·克拉克·麦克斯韦在他 1861 年的论文《物理力线》中首次注意到这一事实。[33] 在论文的第二部分下半部分中,麦克斯韦为这两种现象分别给出了不同的物理解释。
一些现代教科书提及了电磁感应的这两个方面。[34] 正如理查德·费曼所述:
因此,“磁通规则”——即回路中的电动势等于回路中磁通量的变化率——适用于无论磁通变化是因为磁场改变还是因为回路运动(或两者同时发生)......
然而,在对这一规则的解释中,我们分别使用了两种完全不同的规律来描述这两种情况——对于 “回路运动”,使用 \(\mathbf{v} \times \mathbf{B}\);对于 “磁场变化”,使用 \(\nabla \times \mathbf{E} = -\partial_t \mathbf{B}\)。
在物理学的其他地方,我们尚未发现另一个简单而准确的通用原则,其真实理解需要基于两种不同现象的分析。
——理查德·P·费曼,《费曼物理学讲义》[35]
基于四维形式的解释
在一般情况下,仅通过磁力作用于移动导线或改变面积的回路中的电荷来解释运动电动势的出现是不充分的。事实上,导线或回路中可能完全没有电荷,那么在这种情况下,电磁感应效应是否会消失?这类情形在某篇文章中被分析,该文将电磁场的积分方程以四维协变形式书写,并在法拉第定律中引入了回路内磁通量的**全时间导数**,而非偏时间导数。[36] 因此,电磁感应效应可以在磁场随时间变化时出现,也可以在回路面积变化时出现。
从物理的角度来看,与其讨论感应电动势,不如讨论回路中由于磁通量变化而出现的感应电场强度 \(\mathbf{E} = -\nabla \mathcal{E} - \frac{\partial \mathbf{A}}{\partial t}\)。在这种情况下,由磁场变化引起的电场 \(\mathbf{E}\) 的贡献通过项 \(-\frac{\partial \mathbf{A}}{\partial t}\) 实现,其中 \(\mathbf{A}\) 是矢量势。
如果在恒定磁场中,回路面积发生变化,那么回路的某些部分不可避免地会运动。在这种情况下,在与回路共动的参考系 \(K'\) 中,由静止参考系 \(K\) 中通过回路的磁场 \(\mathbf{B}\) 的洛伦兹变换会导致电场 \(\mathbf{E}\) 的出现。在 \(K'\) 中,该电场 \(\mathbf{E}\) 被视为移动回路中感应效应的结果,而无论回路中是否存在电荷。
在导电回路中,电场 \(\mathbf{E}\) 会引起电荷的运动。在参考系 \(K\) 中,这表现为感应电动势 \(\mathcal{E}\) 的出现,其沿回路的梯度形式 \(-\nabla \mathcal{E}\) 似乎生成了电场 \(\mathbf{E}\)。
爱因斯坦的观点
对这种表面上的两分法的反思,是促使阿尔伯特·爱因斯坦发展特殊相对论的主要路径之一:
众所周知,麦克斯韦电动力学——按照当今通常的理解——当应用于运动的物体时,会导致一些不对称性,而这些不对称性似乎并不是现象本身所固有的。以磁铁与导体的相互电动力作用为例。
这里的可观察现象仅取决于导体和磁铁的相对运动,而传统观点却在两种情况之间做了明显区分:一种是磁铁运动而导体静止,另一种是导体运动而磁铁静止。对于第一种情况,当磁铁运动而导体静止时,在磁铁附近会产生具有一定能量的电场,这种电场在导体所在的部分产生电流。
但是,如果磁铁静止而导体运动,磁铁附近不会产生电场。然而,在导体中,我们发现了一种电动势,其本身没有对应的能量来源,但它会引发——假设在上述两种情况下相对运动是相等的——与第一种情况下由电场产生的电流具有相同路径和强度的电流。
这一类现象,加上试图发现地球相对于 “光媒质” 的任何运动的失败尝试,表明电动力学和力学的现象都没有与绝对静止的概念相对应的属性。
——阿尔伯特·爱因斯坦,《论运动物体的电动力学》[37]
6. 参见
- 涡流 (Eddy current)
- 电感 (Inductance)
- 麦克斯韦方程组 (Maxwell's equations)
- 串扰 (Crosstalk)
- 法拉第悖论 (Faraday paradox)
- 菲利奇定律 (Felici's law)
7. 参考文献
1. Poyser, Arthur William (1892).Magnetism and Electricity: A manual for students in advanced classes. 伦敦与纽约: Longmans, Green, & Co. 图 248, 第 245 页. 检索于 2009-08-06.
2. Sadiku, M. N. O. (2007). Elements of Electromagnetics (第 4 版). 纽约 & 牛津: 牛津大学出版社. 第 386 页. ISBN 978-0-19-530048-2.
3. "Applications of electromagnetic induction". 波士顿大学. 检索日期: 1999-07-22.
4. "A Brief History of Electromagnetism"(PDF).
5. Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (第 5 版). Pearson: Prentice Hall. 第 255 页. ISBN 978-0-13-241326-8.
6. "Joseph Henry". 美国国家科学院会员目录. 检索于 2016-12-30.
7. Giancoli, Douglas C. (1998).Physics: Principles with Applications (第 5 版). 第 623–624 页.
8. Faraday, Michael (1831-08-29)."Faraday's notebooks: Electromagnetic Induction" (PDF). 英国皇家学会. 来源于[原始文档](https://royalsociety.org/). 检索于 2021-08-30.
9. Faraday, Michael; Day, P. (1999-02-01).The philosopher's tree: a selection of Michael Faraday's writings. CRC 出版社. 第 71 页. ISBN 978-0-7503-0570-9. 检索于 2011-08-28.
10. Williams, L. Pearce (1965).Michael Faraday. 纽约: Basic Books. [完整引文待补充].
11. Clerk Maxwell, James (1904).A Treatise on Electricity and Magnetism. 第 2 卷 (第三版). 牛津大学出版社. 第 178–179 页, 第 189 页。
12. "Archives Biographies: Michael Faraday". 工程与技术学会 (Institution of Engineering and Technology)。
13. Lenz, Emil (1834)."Ueber die Bestimmung der Richtung der durch elektodynamische Vertheilung erregten galvanischen Ströme".《物理与化学年鉴》(Annalen der Physik und Chemie). 107 (31): 483–494. Bibcode:1834AnP...107..483L. doi:[10.1002/andp.18341073103](https://doi.org/10.1002/andp.18341073103)。
部分论文的英文翻译可参考 Magie, W. M. (1963). A Source Book in Physics.剑桥, 马萨诸塞州: 哈佛大学出版社. 第 511–513 页。
14. Siegel, Ethan (2019 年 3 月 1 日). "Relativity Wasn't Einstein's Miracle; It Was Waiting In Plain Sight For 71 Years".Forbes. 来源于 2023 年 7 月 3 日的[原始档案](https://www.forbes.com)。检索于 2023 年 7 月 3 日。
15. Siegel, Ethan (2023 年 6 月 28 日). "71 years earlier, this scientist beat Einstein to relativity - Michael Faraday's 1834 law of induction was the key experiment behind the eventual discovery of relativity. Einstein admitted it himself". Big Think. 来源于 2023 年 6 月 28 日的[原始档案](https://bigthink.com)。检索于 2023 年 7 月 3 日。
16. Jordan, Edward; Balmain, Keith G. (1968). Electromagnetic Waves and Radiating Systems (第二版). Prentice-Hall. 第 100 页。
"法拉第定律指出,围绕闭合路径的电动势等于该路径所包围的磁通量随时间的负变化率。"
17. Hayt, William (1989).Engineering Electromagnetics (第五版). McGraw-Hill. 第 312 页. ISBN 0-07-027406-1.
"磁通量是指穿过任何封闭路径周边的表面的磁场通量。"
18. Feynman, Richard P."The Feynman Lectures on Physics Vol. II."feynmanlectures.caltech.edu. 检索于 2020 年 11 月 7 日。
19. Griffiths, David J. (1999).Introduction to Electrodynamics (第三版). 上鞍河, 新泽西州: Prentice Hall. 第 301–303 页. ISBN 0-13-805326-X.
20. Tipler, Mosca (2004).Physics for Scientists and Engineers.Macmillan. 第 795 页. ISBN 9780716708100.
21. Neumann, Franz Ernst (1846)."Allgemeine Gesetze der inducirten elektrischen Ströme." Annalen der Physik. 143 (1): 31–44. Bibcode:1846AnP...143...31N. doi:10.1002/andp.18461430103. 原始文件存档于 2020 年 3 月 12 日。
22. Yehuda Salu (2014)."A Left Hand Rule for Faraday's Law."The Physics Teacher. 52 (1): 48. Bibcode:2014PhTea..52...48S. doi:10.1119/1.4849156. [视频解释链接](https://doi.org)。
23. Salu, Yehuda."Bypassing Lenz's Rule - A Left Hand Rule for Faraday's Law." www.PhysicsForArchitects.com. 原始文件存档于 2020 年 5 月 7 日。检索于 2017 年 7 月 30 日。
24. Whelan, P. M.; Hodgson, M. J. (1978).Essential Principles of Physics. 第二版. John Murray. ISBN 0-7195-3382-1.
25. Nave, Carl R."Faraday's Law." HyperPhysics. Georgia State University. 检索于 2011 年 8 月 29 日。
26. Griffiths, David J. (2017).Introduction to Electrodynamics.第四版. Cambridge University Press. ISBN 978-1-108-42041-9. OCLC 965197645.
27. Harrington, Roger F. (2003). ntroduction to Electromagnetic Engineering. Mineola, NY: Dover Publications. 第 56 页. ISBN 0-486-43241-6.
28. Davison, M. E. (1973)."A Simple Proof that the Lorentz Force, Law Implied Faraday's Law of Induction, when B is Time Independent." American Journal of Physics. 41 (5): 713. Bibcode:1973AmJPh..41..713D. doi:10.1119/1.1987339.
29. Krey, Owen (2007 年 8 月 14 日).Basic Theoretical Physics: A Concise Overview.* Springer. 第 155 页. ISBN 9783540368052.
30. Simonyi, K. (1973). Theoretische Elektrotechnik (第五版). 柏林: VEB Deutscher Verlag der Wissenschaften. eq. 20, 第 47 页.
31. Stewart, Joseph V.Intermediate Electromagnetic Theory. 第 396 页. “关于法拉第定律(即同极发电机)的例子,明确表明在扩展体的情况下,必须注意选择边界以确定磁通量,边界不能保持静止,而必须相对于物体运动。”
32. Hughes, W. F.; Young, F. J. (1965).The Electromagnetodynamics of Fluid. John Wiley. Eq. (2.6–13) 第 53 页.
33. Clerk Maxwell, James (1861)."On physical lines of force"Philosophical Magazine. 90. Taylor & Francis: 11–23. doi:10.108014786431003659180. S2CID 135524562.
34. Griffiths, David J. (1999).Introduction to Electrodynamics (第 3 版). Upper Saddle River, NJ: Prentice Hall. 第 301–303 页. ISBN 0-13-805326-X.
请注意,与电磁动势(emf)相关的通量定律,在这篇文章中被称为 “法拉第定律”,在 Griffiths 的术语中被称为 “通用通量定律”(universal flux rule)。Griffiths 使用术语 “法拉第定律” 指代本文所称的 “麦克斯韦-法拉第方程”。因此,在教材中,Griffiths 的陈述实际上是关于 “通用通量定律” 的。
35. 《费曼物理学讲义》第二卷,第 17 章:感应定律 (*The Feynman Lectures on Physics Vol. II Ch. 17: The Laws of Induction*).
36. Fedosin, Sergey G. (2019)."On the Covariant Representation of Integral Equations of the Electromagnetic Field".* Progress in Electromagnetics Research C. 96: 109–122. arXiv:1911.11138. Bibcode:2019arXiv191111138F. doi:10.2528/PIERC19062902. S2CID 208095922.
37. Einstein, Albert."On the Electrodynamics of Moving Bodies". (PDF).
8. 延伸阅读
克拉克·麦克斯韦,詹姆斯 (1881). 《电学与磁学论》,第二卷 (A Treatise on Electricity and Magnetism, Vol. II). 牛津:克拉伦登出版社 (Oxford: Clarendon Press). 第三章,第 530 节,第 178 页. ISBN 0-486-60637-6. 《电学与磁学论》。
9. 外部链接
- 与法拉第感应定律相关的媒体 - Wikimedia Commons
- 一个关于电磁感应的简单交互式教程(点击并拖动磁铁来回移动)- 国家高磁场实验室 (National High Magnetic Field Laboratory)
- Roberto Vega.《感应:法拉第定律和楞次定律》 - 高度动画化的讲座,带有音效,来自《电学与磁学课程页面》
- 物理与天文学笔记 - HyperPhysics,乔治亚州立大学 (Georgia State University)
- Tankersley 和 Mosca:《介绍法拉第定律》(PDF)
- 一个关于运动电动势的免费模拟