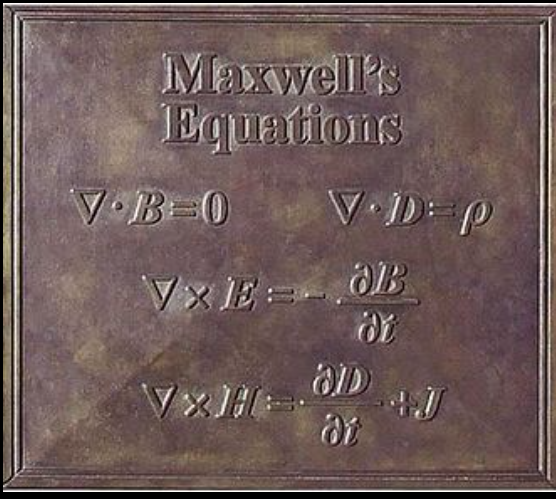麦克斯韦方程组(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。
麦克斯韦方程组,或称麦克斯韦–赫维赛德方程组,是一组耦合偏微分方程,与洛伦兹力定律一起构成了经典电磁学、经典光学、电路和磁路的基础。这些方程为电学、光学和无线电技术(如发电、电动机、无线通信、透镜、雷达等)提供了数学模型。它们描述了电场和磁场如何由电荷、电流及场的变化产生。\(^\text{[注 1]}\) 这些方程以物理学家和数学家詹姆斯·克拉克·麦克斯韦的名字命名,他在 1861 年和 1862 年首次发表了包含洛伦兹力定律的早期方程形式。麦克斯韦最早使用这些方程提出光是一种电磁现象。方程的现代形式及其最常见的表述归功于奥利弗·赫维赛德。\(^\text{[1]}\)
麦克斯韦方程组可以组合起来,展示电磁场的波动(波)如何以恒定速度 \( c \)(真空中为 299792458 m/s[2])传播。这种波动称为电磁辐射,其以不同的波长出现,从而产生从无线电波到伽马射线的辐射谱。
在偏微分方程形式和一致的单位制中,麦克斯韦的微观方程可以写成: \[ \begin{aligned} \nabla \cdot \mathbf{E} &= \frac{\rho}{\varepsilon_0} \\ \nabla \cdot \mathbf{B} &= 0 \\ \nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \times \mathbf{B} &= \mu_0 \left(\mathbf{J} + \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\right) \end{aligned}~ \] 其中,\(\mathbf{E}\) 表示电场,\(\mathbf{B}\) 表示磁场,\(\rho\) 为电荷密度,\(\mathbf{J}\) 为电流密度,\(\varepsilon_0\) 为真空电容率,\(\mu_0\) 为真空磁导率。
这些方程有两个主要变体:
- 微观方程具有普遍适用性,但在常规计算中不便使用。它们将电场和磁场与总电荷和总电流联系起来,包括原子尺度上复杂的材料内部电荷和电流。
- 宏观方程定义了两个新的辅助场,用于描述物质的宏观行为,而不必考虑原子尺度的电荷和量子现象(如自旋)。但其使用需要实验确定的参数,以表征材料对电磁的响应。
“麦克斯韦方程” 一词通常也用于指等效的替代形式。基于电标势和磁标势的麦克斯韦方程版本常用于显式求解边值问题、分析力学或量子力学。协变形式(在时空中,而非分离的空间和时间)使得麦克斯韦方程与狭义相对论的兼容性显而易见。在高能物理和引力物理中常用的曲时空中的麦克斯韦方程与广义相对论相容。\(^\text{[注 2]}\) 实际上,阿尔伯特·爱因斯坦发展了狭义和广义相对论,以容纳麦克斯韦方程中光速不变的结果,遵循只有相对运动才具有物理意义的原则。
这些方程的发表标志着对之前分别描述的现象——磁、静电、光及相关辐射——的理论统一。从 20 世纪中期以来,人们理解到麦克斯韦方程并未精确描述电磁现象,而是更精确的量子电动力学理论的经典极限。
1. 方程的历史
主条目:麦克斯韦方程的历史
2. 概念描述
高斯定律
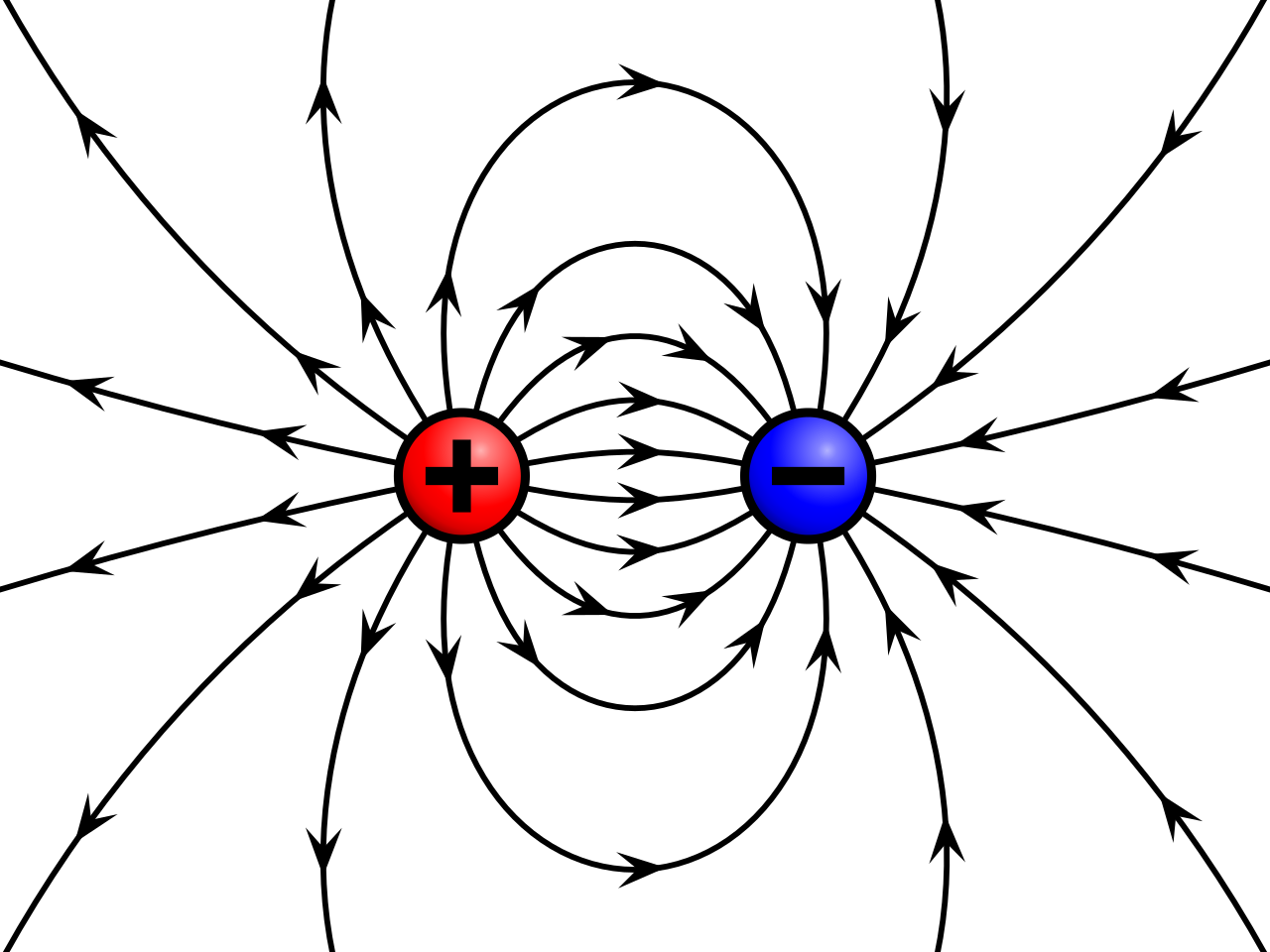
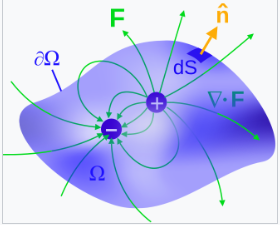
高斯定律描述了电场与电荷之间的关系:电场从正电荷向外指向负电荷,电场通过闭合表面的净流出量与所包围的电荷成正比,包括由于材料极化产生的束缚电荷。该比例系数为真空介电常数。
磁场的高斯定律
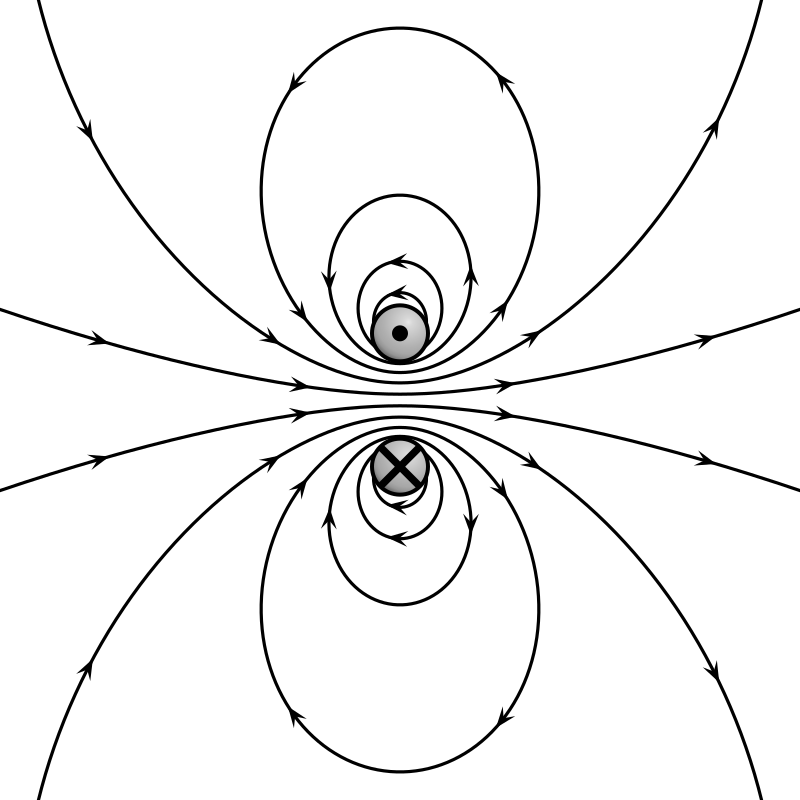
磁场的高斯定律指出,电荷没有磁性对应物,称为磁单极子;不存在孤立的北极或南极。\(^\text{[3]}\) 相反,材料的磁场归因于偶极子,磁场通过闭合表面的净流出量为零。磁偶极子可以表示为电流回路或不可分离的相等且相反的 “磁荷” 对。具体来说,通过高斯面的总磁通量为零,磁场是一个螺线型矢量场。
法拉第定律
法拉第感应定律的麦克斯韦-法拉第形式描述了一个随时间变化的磁场如何与电场的旋度相关联。\(^\text{[3]}\) 其积分形式表明,将电荷绕闭合回路移动所需的单位电荷功等于穿过所围表面的磁通量变化率。
电磁感应是许多电力发电机的工作原理:例如,旋转的条形磁铁会产生变化的磁场,并在附近的导线上生成电场。
安培–麦克斯韦定律
安培定律的原始形式表明磁场与电流有关。麦克斯韦的补充指出,磁场也与变化的电场有关,麦克斯韦称之为位移电流。积分形式表明,电流和位移电流与沿着任意封闭曲线的磁场成正比。
麦克斯韦对安培环路定律的修改很重要,因为否则安培和高斯的定律必须针对静电场进行调整。\(^\text{[4]}\) 这一修改的一个结果是预测出随着电场变化而出现的旋转磁场。\(^\text{[3][5]}\) 进一步的结果是预测出自维持的电磁波在空旷空间中传播。
从电荷和电流实验中预测出的电磁波速度与光速相匹配;事实上,光是一种电磁辐射(如 X 射线、无线电波等)。麦克斯韦在 1861 年认识到电磁波与光的联系,从而统一了电磁学和光学理论。
3. 以电场和磁场(微观或真空版)形式的表述
在电场和磁场的表述中,有四个方程用于确定给定电荷和电流分布的场。另有一条独立的自然法则,即洛伦兹力定律,描述了电场和磁场如何作用于带电粒子和电流。按照惯例,麦克斯韦的原始方程中包含的这一定律版本现已不再包括在内。下列矢量微积分形式是奥利弗·赫维赛德的工作成果,\(^\text{[6][7]}\) 并已成为标准。该形式具有旋转不变性,因此比麦克斯韦最初以 x、y 和 z 分量表达的 20 个方程在数学上更加透明。相对论性表述更加对称且满足洛伦兹不变性。同样的方程也可以用张量微积分或微分形式表达(见 “§ 替代表述” 部分)。
微分和积分表述在数学上是等价的;二者均有其用途。积分形式将空间区域内的场与边界上的场联系起来,通常可以用于简化计算,并直接从对称的电荷和电流分布中计算场。另一方面,微分方程是纯粹的局部方程,是在计算更复杂(非对称)情况中的场时更自然的起点,例如使用有限元分析。\(^\text{[8]}\)
符号说明
除非另有说明,加粗符号代表向量量,斜体符号代表标量量。方程引入了电场 \( E \)(一个向量场)和磁场 \( B \)(一个伪向量场),它们通常都随时间和位置变化。方程中的源项是:
- 总电荷密度(每单位体积的总电荷)\( \rho \),以及
- 总电流密度(每单位面积的总电流)\( J \)。
方程中出现的通用常数(前两个常数仅在国际单位制(SI)表述中明确出现)包括:
- 真空介电常数 \( \varepsilon_0 \),
- 真空磁导率 \( \mu_0 \),以及
- 光速 \( c = (\varepsilon_0 \mu_0)^{-1/2} \)。
微分方程
在微分方程中,
- 纳布拉符号 \( \nabla \) 表示三维梯度算符(即 “del” 算符),
- \( \nabla \cdot \) 符号(读作 “del dot”)表示散度算符,
- \( \nabla \times \) 符号(读作 “del cross”)表示旋度算符。
积分方程
在积分方程中,
- \( \Omega \) 是具有封闭边界表面 \( \partial \Omega \) 的任意体积,
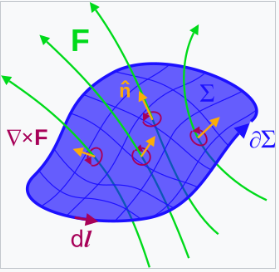
- \( \Sigma \) 是具有封闭边界曲线 \( \partial \Sigma \) 的任意曲面。
这些方程在时间不变的表面和体积下更容易理解。时间不变的表面和体积是‘固定的’,在给定的时间间隔内不会变化。例如,由于表面是时间不变的,我们可以在法拉第定律中将微分符号带到积分符号下: \[ \frac{\mathrm{d}}{\mathrm{d} t} \iint_{\Sigma} \mathbf{B} \cdot \mathrm{d} \mathbf{S} = \iint_{\Sigma} \frac{\partial \mathbf{B}}{\partial t} \cdot \mathrm{d} \mathbf{S} \,,~ \] 麦克斯韦方程组可以通过使用适当的高斯和斯托克斯公式,并使用可能依赖时间的表面和体积,以微分形式来表示。
- \(\iint_{\partial \Omega}\) 表示在边界表面 ∂Ω 上的曲面积分,其中环路表示该表面是闭合的。
- \(\iiint_{\Omega}\) 表示在体积 Ω 上的体积积分。
- \(\oint_{\partial \Sigma}\) 表示在边界曲线 ∂Σ 上的线积分,其中环路表示该曲线是闭合的。
- \(\iint_{\Sigma}\) 表示在表面 Σ 上的曲面积分。
封闭在体积 Ω 内的总电荷 \( Q \) 是在 Ω 上的电荷密度 ρ 的体积积分(参见下面的‘宏观表述’部分): \[ Q = \iiint_{\Omega} \rho \, \mathrm{d} V,~ \] 其中 \( \mathrm{d} V \) 是体积微分元。
总磁通量 \( \Phi_B \) 是通过固定表面 Σ 的磁场 B 的曲面积分: \[ \Phi_B = \iint_{\Sigma} \mathbf{B} \cdot \mathrm{d} \mathbf{S},~ \] 总电通量 \( \Phi_E \) 是通过 Σ 的电场 E 的曲面积分: \[ \Phi_E = \iint_{\Sigma} \mathbf{E} \cdot \mathrm{d} \mathbf{S},~ \] 总电流 \( I \) 是通过 Σ 的电流密度 J 的曲面积分: \[ I = \iint_{\Sigma} \mathbf{J} \cdot \mathrm{d} \mathbf{S},~ \] 其中 \( \mathrm{d} \mathbf{S} \) 表示与表面 Σ 垂直的微分表面积矢量(矢量面积有时用 A 而不是 S 表示,但这与磁矢量势的符号冲突)。
4. 以国际单位制量进行表述
| 名称 | 积分形式 | 微分形式 |
| 高斯定律 | \(\oint_{\partial \Omega} \mathbf{E} \cdot \mathrm{d} \mathbf{S} = \frac{1}{\varepsilon_0} \iiint_{\Omega} \rho \, \mathrm{d}V\) | \(\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}\) |
| 磁场的高斯定律 | \(\oint_{\partial \Omega} \mathbf{B} \cdot \mathrm{d} \mathbf{S} = 0\) | \(\nabla \cdot \mathbf{B} = 0\) |
| 麦克斯韦-法拉第方程(法拉第电磁感应定律) | \(\oint_{\partial \Sigma} \mathbf{E} \cdot \mathrm{d} \ell = - \frac{\mathrm{d}}{\mathrm{d} t} \iint_{\Sigma} \mathbf{B} \cdot \mathrm{d} \mathbf{S}\) | \(\nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t}\) |
| 安培-麦克斯韦方程 | \(\oint_{\partial \Sigma} \mathbf{B} \cdot \mathrm{d} \ell = \mu_0 \left( \iint_{\Sigma} \mathbf{J} \cdot \mathrm{d} \mathbf{S} + \varepsilon_0 \frac{\mathrm{d}}{\mathrm{d} t} \iint_{\Sigma} \mathbf{E} \cdot \mathrm{d} \mathbf{S} \right)\) | \(\nabla \times \mathbf{B} = \mu_0 \left( \mathbf{J} + \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right)\) |
5. 使用高斯单位制的表述
可以通过将带有维度的因子 \( \varepsilon_0 \) 和 \( \mu_0 \) 吸收到单位中(从而重新定义它们),来简化电荷、电场和磁场的定义,以便于理论计算。配合洛伦兹力定律中的量值变化,这将产生相同的物理效果,例如带电粒子的轨迹或电动机所做的功。这些定义在理论物理和高能物理中更为常用,因为此时将电场和磁场设置为相同单位可以简化电磁张量的表示:统一电场和磁场的洛伦兹协变对象将包含具有统一单位和维度的分量。\(^\text{[9]:vii}\) 高斯单位制中”,麦克斯韦方程变为:\(^\text{[11]}\)
| 名称 | 积分方程 | 微分方程 |
| 高斯定律 | \( \iint_{\partial \Omega} \mathbf{E} \cdot d\mathbf{S} = 4\pi \iiint_{\Omega} \rho \, dV \) | \( \nabla \cdot \mathbf{E} = 4\pi \rho \) |
| 磁场的高斯定律 | \( \iint_{\partial \Omega} \mathbf{B} \cdot d\mathbf{S} = 0 \) | \( \nabla \cdot \mathbf{B} = 0 \) |
| 麦克斯韦-法拉第方程(法拉第感应定律) | \( \oint_{\partial \Sigma} \mathbf{E} \cdot d\boldsymbol{\ell} = -\frac{1}{c} \frac{d}{dt} \iint_{\Sigma} \mathbf{B} \cdot d\mathbf{S} \) | \( \nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}}{\partial t} \) |
| 安培-麦克斯韦方程 | \( \oint_{\partial \Sigma} \mathbf{B} \cdot d\boldsymbol{\ell} = \frac{1}{c} \left( 4\pi \iint_{\Sigma} \mathbf{J} \cdot d\mathbf{S} + \frac{d}{dt} \iint_{\Sigma} \mathbf{E} \cdot d\mathbf{S} \right) \) | \( \nabla \times \mathbf{B} = \frac{1}{c} \left( 4\pi \mathbf{J} + \frac{\partial \mathbf{E}}{\partial t} \right) \) |
当选择一个以光速 \( c \) 为单位的量纲系统进行无量纲化时,方程会稍微简化,这样秒和光秒可以互换使用,并且 \( c = 1 \)。
进一步的简化可以通过吸收 \( 4\pi \) 的因子来实现。这个过程称为 “有理化”,会影响库仑定律或高斯定律是否包含此类因子(参见主要用于粒子物理的海维赛德-洛伦兹单位制)。
6. 微分形式和积分形式之间的关系
微分形式和积分形式的等价性是高斯散度定理和开尔文–斯托克斯定理的结果。
通量与散度
根据纯粹的数学高斯散度定理,边界面 ∂Ω 上的电通量可以重写为:
\[\iint_{\scriptstyle \partial \Omega} \mathbf{E} \cdot \mathrm{d} \mathbf{S} = \iiint_{\Omega} \nabla \cdot \mathbf{E} \, \mathrm{d} V~\]
因此,高斯方程的积分形式可以重写为:
\[\iiint_{\Omega} \left(\nabla \cdot \mathbf{E} - \frac{\rho}{\varepsilon_0}\right) \, \mathrm{d} V = 0~\]
由于 Ω 是任意的(例如,任意小的球且中心任意),只有当被积函数在各处为零时,这个方程才成立。这便是高斯方程的微分形式,仅需进行微小的重排。
类似地,将高斯磁定律的积分形式中的磁通量重写为:
\[\iint_{\scriptstyle \partial \Omega} \mathbf{B} \cdot \mathrm{d} \mathbf{S} = \iiint_{\Omega} \nabla \cdot \mathbf{B} \, \mathrm{d} V = 0.~\]
对于所有的 Ω,当且仅当 \(\nabla \cdot \mathbf{B} = 0\) 在各处成立时,这个等式才成立。
环量与旋度
根据开尔文-斯托克斯定理,我们可以将围绕封闭边界曲线 ∂Σ 的场的线积分重写为其环量(即它们的旋度)在该曲线所包围的表面上的积分,即 \[ \oint _{\partial \Sigma }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{\Sigma }(\nabla \times \mathbf {B} )\cdot \mathrm {d} \mathbf {S} ,~ \] 因此,安培-麦克斯韦定律(安培回路定律的修正版本)的积分形式可以重写为 \[ \iint _{\Sigma }\left(\nabla \times \mathbf {B} -\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)\right)\cdot \mathrm {d} \mathbf {S} =0.~ \] 由于可以任意选择 Σ,例如作为任意小、任意取向、任意中心的圆盘,我们得出结论,只有当微分形式的安培-麦克斯韦定律满足时,积分形式才成立。类似地,法拉第定律的微分和积分形式的等价性也是如此。
线积分和旋度与经典流体力学中的量类似:流体的环量是流体流速场沿封闭回路的线积分,而流体的涡度是速度场的旋度。
7. 电荷守恒
电荷不变性可以作为麦克斯韦方程组的推论得出。通过散度-旋度恒等式,安培-麦克斯韦定律的左侧具有零散度。展开右侧的散度,交换导数并应用高斯定律,得到: \[ 0 = \nabla \cdot (\nabla \times \mathbf{B}) = \nabla \cdot \left(\mu_{0} \left(\mathbf{J} + \varepsilon_{0} \frac{\partial \mathbf{E}}{\partial t}\right)\right) = \mu_{0} \left(\nabla \cdot \mathbf{J} + \varepsilon_{0} \frac{\partial}{\partial t} \nabla \cdot \mathbf{E}\right) = \mu_{0} \left(\nabla \cdot \mathbf{J} + \frac{\partial \rho}{\partial t}\right)~\] 即: \[ \frac{\partial \rho}{\partial t} + \nabla \cdot \mathbf{J} = 0.~ \] 根据高斯散度定理,这意味着在固定体积内电荷的变化率等于穿过边界的净电流: \[ \frac{d}{dt} Q_{\Omega} = \frac{d}{dt} \iiint_{\Omega} \rho \, \mathrm{d} V = -\iint_{\partial \Omega} \mathbf{J} \cdot \mathrm{d} \mathbf{S} = -I_{\partial \Omega}.~ \] 特别是在一个孤立系统中,总电荷是守恒的。
8. 真空方程、电磁波与光速
在没有电荷(ρ = 0)和电流(J = 0)的区域(如真空中),麦克斯韦方程简化为: \[ \nabla \cdot \mathbf{E} = 0, \quad \nabla \times \mathbf{E} + \frac{\partial \mathbf{B}}{\partial t} = 0, \quad \nabla \cdot \mathbf{B} = 0, \quad \nabla \times \mathbf{B} - \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} = 0.~ \] 取旋度方程的旋度(∇×),并使用旋度的旋度恒等式,我们得到: \[ \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{E}}{\partial t^2} - \nabla^2 \mathbf{E} = 0,~ \] \[ \mu_0 \varepsilon_0 \frac{\partial^2 \mathbf{B}}{\partial t^2} - \nabla^2 \mathbf{B} = 0.~ \] 这两个方程分别描述了电场 \(\mathbf{E}\) 和磁场 \(\mathbf{B}\) 的波动行为。
该量 \(\mu_0 \varepsilon_0\) 的维度为 (T/L)\(^2\)。定义 \[ c = (\mu_0 \varepsilon_0)^{-1/2}~ \] 后,上述方程具有标准波动方程的形式: \[ \frac{1}{c^2} \frac{\partial^2 \mathbf{E}}{\partial t^2} - \nabla^2 \mathbf{E} = 0,~ \] \[ \frac{1}{c^2} \frac{\partial^2 \mathbf{B}}{\partial t^2} - \nabla^2 \mathbf{B} = 0.~ \] 在麦克斯韦的时代,已知的 \(\varepsilon_0\) 和 \(\mu_0\) 的值给出 \(c \approx 2.998 \times 10^8\) m/s,这是当时已知的真空中光速。由此他提出光和无线电波是传播的电磁波,这一理论已被充分证实。在旧的 SI 单位制中,\(\mu_0 = 4\pi \times 10^{-7}\) 和 \(c = 299,792,458~\text{m/s}\) 是定义常数(这意味着定义了 \(\varepsilon_0 = 8.8541878... \times 10^{-12}~\text{F/m}\),从而定义了安培和米)。在新的 SI 单位制中,只有 \(c\) 保持定义值,并且电子电荷具有定义值。
在具有相对介电常数 \(\varepsilon_r\) 和相对磁导率 \(\mu_r\) 的材料中,光的相速度变为 \[ v_{\text{p}} = \frac{1}{\sqrt{\mu_0 \mu_r \varepsilon_0 \varepsilon_r}},~ \] 通常比 \(c\) 小(见注释 5)。
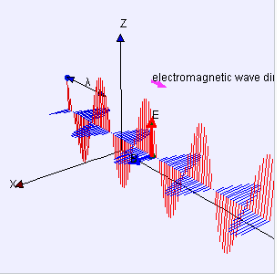
此外,\(\mathbf{E}\) 和 \(\mathbf{B}\) 相互垂直,且与波传播方向也垂直,并且它们是相位一致的。正弦平面波是这些方程的一种特殊解。麦克斯韦方程解释了这些波如何能够物理地在空间中传播。变化的磁场通过法拉第定律产生变化的电场,反过来,这个电场通过麦克斯韦对安培环路定律的修正产生变化的磁场。这种循环使得这些波(现在称为电磁辐射)可以以速度 \(c\) 在空间中传播。
9. 宏观表述
上述方程为麦克斯韦方程的微观版本,以(可能是原子级别的)电荷和电流来表示电场和磁场。这有时被称为 “通用” 形式,但下面的宏观版本同样具有通用性,不同之处在于记账方式。
微观版本有时称为 “真空中的麦克斯韦方程”,因为方程的结构中并未包含物质介质,而是仅在电荷和电流项中出现。微观版本由洛伦兹引入,他试图利用这一版本从微观成分推导出物质的宏观特性。
“麦克斯韦的宏观方程”,也称为 “物质中的麦克斯韦方程”,与麦克斯韦本人引入的方程更加相似。
| 名称 | 积分形式方程 (SI 单位) | 微分形式方程 (SI 单位) | 微分形式方程 (高斯单位) |
| 高斯定律 | $\iint_{\partial \Omega} \mathbf{D} \cdot d\mathbf{S} = \iiint_{\Omega} \rho_f \, dV$ | $\nabla \cdot \mathbf{D} = \rho_f$ | $\nabla \cdot \mathbf{D} = 4\pi \rho_f$ |
| 安培-麦克斯韦定律 | $\int_{\partial \Sigma} \mathbf{H} \cdot d\mathbf{\ell} = \iint_{\Sigma} \mathbf{J_f} \cdot d\mathbf{S} + \frac{d}{dt} \iint_{\Sigma} \mathbf{D} \cdot d\mathbf{S}$ | $\nabla \times \mathbf{H} = \mathbf{J_f} + \frac{\partial \mathbf{D}}{\partial t}$ | $\nabla \times \mathbf{H} = \frac{1}{c} \left( 4\pi \mathbf{J_f} + \frac{\partial \mathbf{D}}{\partial t} \right)$ |
| 磁场的高斯定律 | $\iint_{\partial \Omega} \mathbf{B} \cdot d\mathbf{S} = 0$ | $\nabla \cdot \mathbf{B} = 0$ | $\nabla \cdot \mathbf{B} = 0$ |
| 麦克斯韦-法拉第方程(法拉第感应定律) | $\oint_{\partial \Sigma} \mathbf{E} \cdot d\mathbf{\ell} = - \frac{d}{dt} \iint_{\Sigma} \mathbf{B} \cdot d\mathbf{S}$ | $\nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t}$ | $\nabla \times \mathbf{E} = - \frac{1}{c} \frac{\partial \mathbf{B}}{\partial t}$ |
在宏观方程中,束缚电荷 \( Q_b \) 和束缚电流 \( I_b \) 的影响被包含在位移场 \( D \) 和磁化场 \( H \) 中,而方程仅依赖于自由电荷 \( Q_f \) 和自由电流 \( I_f \)。这反映了将总电荷 \( Q \) 和电流 \( I \)(及其密度 \( \rho \) 和 \( J \))分成自由部分和束缚部分的划分: \[ Q = Q_{\text{f}} + Q_{\text{b}} = \iiint _{\Omega }\left(\rho _{\text{f}}+\rho _{\text{b}}\right)\,\mathrm {d} V=\iiint _{\Omega }\rho \,\mathrm {d} V,~ \] \[ I = I_{\text{f}} + I_{\text{b}} = \iint _{\Sigma }\left(\mathbf {J} _{\text{f}}+\mathbf {J} _{\text{b}}\right)\cdot \mathrm {d} \mathbf {S} =\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} .~ \] 这种划分的代价是需要通过表征方程来确定额外的场 \( D \) 和 \( H \),这些方程将这些场与电场 \( E \) 和磁场 \( B \) 及束缚电荷和电流联系起来。
参见下文,了解微观方程与宏观方程的详细区别。微观方程涉及包括材料贡献的总电荷和总电流,适用于空气/真空环境;而宏观方程处理自由电荷和电流,更适合在材料中使用。
束缚电荷与电流
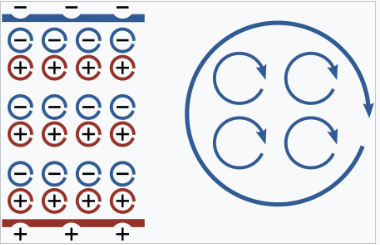
当电场施加到介电材料上时,其分子会通过形成微观电偶极子作出响应——其原子核向电场方向移动一小段距离,而电子则向相反方向移动一小段距离。这在材料中产生了宏观的束缚电荷,尽管所有参与的电荷都束缚在各自的分子中。例如,如果每个分子都以类似图示的方式作出相同的响应,这些微小的电荷移动会合并,在材料的一侧形成一层正束缚电荷,在另一侧形成一层负束缚电荷。束缚电荷最便捷的描述方式是通过材料的极化强度 \( P \),即其每单位体积的偶极矩。如果 \( P \) 是均匀的,则仅在 \( P \) 进入和离开材料的表面处产生宏观的电荷分离。而对于非均匀的 \( P \),材料内部也会产生电荷。[13]
在所有材料中,构成材料的原子会表现出与原子成分的角动量密切相关的磁矩,特别是电子的磁矩。这种与角动量的联系使人联想到一个微观电流环的集合。在材料外部,这样的微观电流环集合与围绕材料表面的宏观电流没有区别,尽管没有任何单个电荷在长距离上移动。这些束缚电流可以用磁化强度 \( M \) 来描述。[14]
因此,非常复杂且细微的束缚电荷和束缚电流可以通过极化强度 \( P \) 和磁化强度 \( M \) 在宏观尺度上表示。\( P \) 和 \( M \) 在足够大的尺度上对这些电荷和电流进行平均,以避免观察到单个原子的细微结构,同时也足够小以在材料中随位置变化。这样,麦克斯韦的宏观方程忽略了许多微观尺度的细节,这些细节在理解宏观尺度的问题时可能并不重要,因为这些方程计算的是在某个适当体积上平均的场。
辅助场、极化与磁化
辅助场的定义为: \[ \mathbf{D}(\mathbf{r}, t) = \varepsilon_0 \mathbf{E}(\mathbf{r}, t) + \mathbf{P}(\mathbf{r}, t),~ \] \[ \mathbf{H}(\mathbf{r}, t) = \frac{1}{\mu_0} \mathbf{B}(\mathbf{r}, t) - \mathbf{M}(\mathbf{r}, t),~ \] 其中 \(\mathbf{P}\) 是极化场,\(\mathbf{M}\) 是磁化场,它们分别通过微观束缚电荷和束缚电流来定义。宏观束缚电荷密度 \(\rho_b\) 和束缚电流密度 \(\mathbf{J}_b\) 关于极化 \(\mathbf{P}\) 和磁化 \(\mathbf{M}\) 定义为: \[ \rho_{\text{b}} = -\nabla \cdot \mathbf{P},~ \] \[ \mathbf{J}_{\text{b}} = \nabla \times \mathbf{M} + \frac{\partial \mathbf{P}}{\partial t}.~ \] 如果我们定义总电荷和电流密度、束缚电荷和电流密度以及自由电荷和电流密度为: \[ \rho = \rho_{\text{b}} + \rho_{\text{f}},~ \] \[ \mathbf{J} = \mathbf{J}_{\text{b}} + \mathbf{J}_{\text{f}},~ \] 并使用上述定义关系来消去 \(\mathbf{D}\) 和 \(\mathbf{H}\),那么 “宏观” 麦克斯韦方程就会再现 “微观” 方程。
本构关系
为了应用 “麦克斯韦的宏观方程”,有必要指定位移场 \(\mathbf{D}\) 与电场 \(\mathbf{E}\) 之间的关系,以及磁化场 \(\mathbf{H}\) 与磁场 \(\mathbf{B}\) 之间的关系。等效地,我们必须指定极化 \(\mathbf{P}\)(因此束缚电荷)和磁化 \(\mathbf{M}\)(因此束缚电流)对施加的电场和磁场的依赖性。指定这种响应的方程称为本构关系。对于实际材料,本构关系很少简单,通常只能近似地描述,并且通常通过实验确定。有关本构关系的更详细描述,请参阅主条目。[15]: 44–45
对于没有极化和磁化的材料,本构关系为(按定义)[9]: 2 \[ \mathbf{D} = \varepsilon_0 \mathbf{E} , \quad \mathbf{H} = \frac{1}{\mu_0} \mathbf{B},~ \] 其中 \(\varepsilon_0\) 是真空介电常数,\(\mu_0\) 是真空磁导率。由于没有束缚电荷,总电荷和自由电荷、电流相等。
对于微观方程的另一种观点是,它们是宏观方程,再加上真空表现为一种没有额外极化和磁化的完美线性 “材料” 的声明。更普遍地,对于线性材料,本构关系为[15]: 44–45 \[ \mathbf{D} = \varepsilon \mathbf{E}, \quad \mathbf{H} = \frac{1}{\mu} \mathbf{B},~ \] 其中 \(\varepsilon\) 是材料的介电常数,\(\mu\) 是材料的磁导率。对于位移场 \(\mathbf{D}\),线性近似通常非常精确,因为除了实验室中能获得的极端电场或温度(如高功率脉冲激光器)之外,材料的原子间电场约为 \(10^{11}\) V/m,远高于外部电场。然而,对于磁化场 \(\mathbf{H}\),线性近似在像铁这样的普通材料中可能失效,导致诸如磁滞现象的发生。不过,即使在线性情况下,也可能存在各种复杂情况。
- 对于均匀材料,\(\varepsilon\) 和 \(\mu\) 在材料中是常量,而对于非均匀材料,它们取决于材料内部的位置(或可能随时间变化)[16]: 463。
- 对于各向同性材料,\(\varepsilon\) 和 \(\mu\) 是标量,而对于各向异性材料(例如由于晶体结构),它们是张量[15]: 421 [16]: 463。
- 材料通常具有色散性,因此 \(\varepsilon\) 和 \(\mu\) 依赖于任何入射电磁波的频率[15]: 625 [16]: 397。
更一般地,对于非线性材料(例如非线性光学),\(\mathbf{D}\) 和 \(\mathbf{P}\) 不一定与 \(\mathbf{E}\) 成正比,类似地,\(\mathbf{H}\) 或 \(\mathbf{M}\) 也不一定与 \(\mathbf{B}\) 成正比。通常,\(\mathbf{D}\) 和 \(\mathbf{H}\) 取决于 \(\mathbf{E}\) 和 \(\mathbf{B}\)、位置、时间以及可能的其他物理量。
在实际应用中,还必须描述自由电流和电荷密度如何与 \(\mathbf{E}\) 和 \(\mathbf{B}\) 相关,可能还与其他物理量(如压力、质量、粒子数密度以及带电粒子的速度)耦合。例如,麦克斯韦给出的原始方程(参见麦克斯韦方程的历史)包括欧姆定律,形式为 \[ \mathbf{J}_{\text{f}} = \sigma \mathbf{E}.~ \]
10. 替代形式
关于特殊相对论中的方程,请参见《经典电磁学和特殊相对论》以及《经典电磁学的协变形式》。
关于广义相对论中的方程,请参见《弯曲时空中的麦克斯韦方程》。
概述请参见《电磁场的数学描述》。
关于量子场论中的方程,请参见《量子电动力学》。
以下列出麦克斯韦方程的几种其他数学形式,列将两组无源麦克斯韦方程与两组有源方程分开。每种形式都有直接基于电场和磁场的版本,以及间接基于电势 \(\varphi\) 和矢势 \(\mathbf{A}\) 的版本。引入势函数是一种便捷的解决无源方程的方法,但一度被认为所有可观察的物理量都包含在电场和磁场中(或相对论地说,是法拉第张量)。然而,在量子力学中,势函数起着关键作用,即使在电场和磁场为零的情况下也能产生可观察的量子力学效应(阿哈罗诺夫-玻姆效应)。
每个表格描述了一种形式。详情请参见主条目。
直接的时空形式展示了麦克斯韦方程在相对论下的不变性,在这种形式中,空间和时间被平等对待。由于这种对称性,电场和磁场被视为法拉第张量的组成部分,从而使得四个麦克斯韦方程减少到两个,简化了方程,尽管不再使用熟悉的矢量形式。麦克斯韦方程中未显式地将空间和时间同等对待的形式中,洛伦兹不变性是一个隐藏的对称性。这也是相对论理论发展中的重要启示来源。实际上,即使是将空间和时间分开处理的形式,也并非非相对论的近似,仅通过重新命名变量来描述相同的物理现象。因此,相对论不变的方程通常仍称为麦克斯韦方程。
下表描述了每种形式。
| 形式 | 齐次方程 | 非齐次方程 |
| 场 闵可夫斯基空间 | \(\partial_{[\alpha} F_{\beta \gamma]} = 0\) | \(\partial_{\alpha} F^{\alpha \beta} = \mu_0 J^{\beta}\) |
| 势(任意规范)闵可夫斯基空间 | \({\displaystyle F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]}}\) | \(2 \partial_{\alpha} \partial^{[\alpha} A^{\beta]} = \mu_{0} J^{\beta}\) |
| 势(洛伦兹规范)闵可夫斯基空间 | \({\displaystyle F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]}}\),\(\partial _{\alpha }A^{\alpha }=0\) | \(\partial _{\alpha }\partial ^{\alpha }A^{\beta }=\mu _{0}J^{\beta }\) |
| 场 任意时空 | \(\partial_{[\alpha} F_{\beta \gamma]} =\qquad \nabla_{[\alpha} F_{\beta \gamma]} = 0\) | \(\frac{1}{\sqrt{-g}} \partial_{\alpha} (\sqrt{-g} F^{\alpha \beta}) = \nabla_{\alpha} F^{\alpha \beta} = \mu_0 J^{\beta}\) |
| 势(任意规范)任意时空(具有§拓扑限制) | \( F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]} \) | \(\frac{2}{\sqrt{-g}} \partial_{\alpha} (\sqrt{-g} \, g^{\alpha \mu} g^{\beta \nu} \partial_{[\mu} A_{\nu]}) = 2 \nabla_{\alpha} ( \nabla^{[\alpha} A^{\beta]}) = \mu_{0} J^{\beta}\) |
| 势(洛伦兹规范)任意时空(具有拓扑限制) | \( F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]} \) \( \nabla _{\alpha }A^{\alpha }=0 \) | \(\nabla _{\alpha } \nabla ^{\alpha } A^{\beta } - R^{\beta }{}_{\alpha } A^{\alpha } = \mu _{0} J^{\beta }\) |
| 形式 | 齐次方程 | 非齐次方程 |
| 字段 任何时空 | \( \mathrm{d} F = 0 \) | \( \mathrm{d} \star F = \mu_0 J \) |
| 势(任意规范)任意时空(具有拓扑限制) | \( F = \mathrm{d} A \) | \( \mathrm{d} \star \mathrm{d} A = \mu_{0} J \) |
| 势(洛伦兹规范)任意时空(具有拓扑限制) | \( F = \mathrm{d} A \)\( \mathrm{d} \star A = 0 \) | \( \star \Box A = \mu_{0} J \) |
- 在张量计算的表述中,电磁张量 \( F_{\alpha \beta} \) 是一个反对称的协变二阶张量;四势 \( A_{\alpha} \) 是一个协变向量;电流 \( J_{\alpha} \) 是一个向量;方括号 [ ] 表示指标的反对称化;\( \partial_{\alpha} \) 是对坐标 \( x^{\alpha} \) 的偏导。在闵可夫斯基空间中,坐标选择与惯性系有关,\( (x^{\alpha}) = (ct, x, y, z) \),因此用于升降指标的度规张量是 \( \eta_{\alpha \beta} = \text{diag}(1, -1, -1, -1) \)。在闵可夫斯基空间上的达朗贝尔算子表示为 \( \Box = \partial_{\alpha} \partial^{\alpha} \),如向量表述中所示。在一般的时空中,坐标系 \( x^{\alpha} \) 是任意的,协变导数 \( \nabla_{\alpha} \)、里奇张量 \( R_{\alpha \beta} \) 以及指标的升降由洛伦兹度规 \( g_{\alpha \beta} \) 定义,达朗贝尔算子定义为 \( \Box = \nabla_{\alpha} \nabla^{\alpha} \)。拓扑限制要求空间的第二实共同调群为零(详细说明参见微分形式表述)。这一条件在去掉一条直线的闵可夫斯基空间中被破坏,此空间可以模拟包含点状磁单极子的(平坦)时空,去掉的直线为其补集。
- 在张量计算的表述中,电磁张量 \( F_{\alpha \beta} \) 是一个反对称的协变二阶张量;四势 \( A_{\alpha} \) 是一个协变向量;电流 \( J_{\alpha} \) 是一个向量;方括号 [ ] 表示指标的反对称化;\( \partial_{\alpha} \) 是对坐标 \( x^{\alpha} \) 的偏导。在闵可夫斯基空间中,坐标选择与惯性系有关,\( (x^{\alpha}) = (ct, x, y, z) \),因此用于升降指标的度规张量是 \( \eta_{\alpha \beta} = \text{diag}(1, -1, -1, -1) \)。在闵可夫斯基空间上的达朗贝尔算子表示为 \( \Box = \partial_{\alpha} \partial^{\alpha} \),如向量表述中所示。在一般的时空中,坐标系 \( x^{\alpha} \) 是任意的,协变导数 \( \nabla_{\alpha} \)、里奇张量 \( R_{\alpha \beta} \) 以及指标的升降由洛伦兹度规 \( g_{\alpha \beta} \) 定义,达朗贝尔算子定义为 \( \Box = \nabla_{\alpha} \nabla^{\alpha} \)。拓扑限制要求空间的第二实共同调群为零(详细说明参见微分形式表述)。这一条件在去掉一条直线的闵可夫斯基空间中被破坏,此空间可以模拟包含点状磁单极子的(平坦)时空,去掉的直线为其补集。
其他表述方法包括几何代数表述和麦克斯韦方程的矩阵表示。在历史上,也曾使用过四元数表述方法。
11. 解法
麦克斯韦方程是一组偏微分方程,用来描述电场与磁场之间的关系以及它们与电荷和电流的关系。通常情况下,电荷和电流本身也依赖于电场和磁场,通过洛伦兹力方程和本构关系来确定。这些方程构成了一组耦合的偏微分方程组,通常非常难以求解:它们的解包括了经典电磁学中的各种复杂现象。以下是一些相关的概述。
和任何偏微分方程一样,要获得唯一解,麦克斯韦方程需要**边界条件**和**初始条件**。例如,即使时空中没有电荷和电流,也有显然的解使得 \( E \) 和 \( B \) 为零或常数,但也存在对应于电磁波的非平凡解。在一些情况下,麦克斯韦方程是在整个空间上求解,边界条件是以无限远处的渐近极限给出的。[23]在其他情况下,麦克斯韦方程是在有限空间区域中求解,并在该区域的边界上给出合适的条件,例如表示外部空间的人工吸收边界、周期性边界条件,[24][25]或将小区域与外界隔离的墙壁(如波导或腔体谐振器)等。[26]
杰菲缅科方程(或密切相关的利纳尔–维希尔势)是麦克斯韦方程的显式解,描述了任何给定电荷和电流分布下所产生的电场和磁场。它假设特定的初始条件以得到所谓的 “延迟解”,即只有电荷产生的场。然而,在电荷和电流本身受到它们所产生的场影响的情况下,杰菲缅科方程并不适用。
在无法获得精确解的情况下,麦克斯韦方程可以通过数值方法来近似求解,例如有限元法和时域有限差分法。[19][21][27][28][29]更多细节可参考计算电磁学。
12. 麦克斯韦方程组的超定性
麦克斯韦方程组似乎是超定的,因为它们涉及六个未知数(电场 \(E\) 和磁场 \(B\) 的三个分量),却有八个方程(两个高斯定律各一个方程,法拉第和安培回路定律各三个向量分量方程)。(电流和电荷不是未知数,因为它们在电荷守恒的条件下是自由指定的。)这与麦克斯韦方程组中某种有限的冗余性有关:可以证明,任何满足法拉第定律和安培回路定律的系统,只要满足系统的初始条件,并假设电荷守恒和不存在磁单极子,该系统就会自动满足两个高斯定律。[30][31] 这一解释最早由朱利叶斯·亚当斯·斯特拉顿于 1941 年提出。[32]
尽管可以在数值算法中简单地忽略两个高斯定律(初始条件除外),但计算精度的不完美可能会导致对这些定律的逐渐违反。通过引入表征这些违反情况的虚拟变量,四个方程就不会再是超定的。得到的这种表达式可以生成更精确的算法,能够同时考虑四条定律。[33]
这两个恒等式 \(\nabla \cdot \nabla \times \mathbf{B} \equiv 0, \quad \nabla \cdot \nabla \times \mathbf{E} \equiv 0\) 将八个方程减少到六个独立方程,是超定性的真正原因。[34][35]
同样,超定性可以视作暗示了电荷和磁荷的守恒,因为在上面描述的推导中需要这些守恒性质,但它们却已由两个高斯定律隐含。
对于线性代数方程,可以制定 “好” 的规则来重写方程和未知数。方程可以是线性相关的。但对于微分方程,特别是偏微分方程 (PDE),需要合适的边界条件,这些条件在方程中的作用并不明显。此外,如果将它们改写为矢量和标量势的形式,由于规范固定,方程会变为欠定。
13. 麦克斯韦方程组作为量子电动力学 (QED) 的经典极限
麦克斯韦方程组和洛伦兹力定律(连同经典电磁学的其余部分)在解释和预测各种现象方面取得了极大的成功。然而,它们未能考虑量子效应,因此其适用范围有限。麦克斯韦方程组通常被认为是量子电动力学的经典极限。
一些观察到的电磁现象无法用麦克斯韦方程组解释。这些现象包括光子-光子散射,以及与光子或虚光子、“非经典光” 和电磁场的量子纠缠相关的许多现象(参见量子光学)。例如,量子密码学无法用麦克斯韦理论描述,甚至无法近似描述。在极强场条件(参见欧拉-海森堡拉格朗日量)或极小尺度下,麦克斯韦方程组的近似性变得愈加明显。
此外,麦克斯韦方程组无法解释涉及单个光子与量子物质相互作用的任何现象,例如光电效应、普朗克定律、杜安-亨特定律和单光子探测器。然而,许多此类现象可以通过量子物质与经典电磁场耦合的半经典理论进行近似描述,经典电磁场可以作为外场或以电荷流和密度的期望值出现在麦克斯韦方程组的右侧。
14. 变体
在作为经典电磁场理论的麦克斯韦方程中,常见的变体相对较少,因为标准方程经受了时间的考验,表现得极为可靠。
磁单极子
麦克斯韦方程假设宇宙中存在电荷,但不存在磁荷(也称为磁单极子)。事实上,尽管经过广泛的搜索,磁荷从未被观察到,[注 7] 并且可能并不存在。如果它们确实存在,那么高斯磁定律和法拉第定律都需要修改,所得的四个方程将会在电场和磁场的互换下完全对称。[9]: 273–275
15. 参见
- 物理空间代数
- 菲涅耳方程
- 引力电磁学
- 电磁场的界面条件
- 运动磁铁与导体问题
- 里曼-西尔伯斯坦矢量
- 时空代数
- 惠勒-费曼吸收理论
16. 说明性注释
- 根据相对论,电场和磁场是单一电磁场的组成部分。
- 然而,在广义相对论中,它们必须通过应力-能量张量进入包含时空曲率的爱因斯坦场方程。
- 场的源/汇的缺失并不意味着场线必须闭合或延伸至无穷远。它们还可以无限绕行而不自相交。此外,在场为零的点(场线无法交叉这些点,因为方向无法定义)周围,可以有一些场线开始,另一些场线结束。例如,在两个相同的圆柱形磁铁之间,中间的磁场为零,而从磁铁发出的轴向场线在此处结束。同时,从该点径向发散出无限多的场线。围绕该点同时存在的结束和开始的场线,保持了场的无散性特征。有关非闭合场线的详细讨论,请参阅 L. Zilberti 的《闭合磁通线的误解》,IEEE Magnetics Letters, vol. 8, art. 1306005, 2017。
- 我们现在称为 \((\varepsilon_0 \mu_0)^{-1/2}\) 的量,具有速度的单位,实际上在麦克斯韦方程出现之前就已经被直接测量了。在 1855 年,威廉·爱德华·韦伯和鲁道夫·科尔劳施进行的一项实验中,他们为一个莱顿瓶(类似电容器)充电,并测量了与电势相关的静电力;然后,他们在放电时测量了放电导线中电流产生的磁力。他们的结果是 \(3.107 \times 10^8 \, \text{m/s}\),与光速非常接近。参见 Joseph F. Keithley, 《电和磁测量的故事:从公元前 500 年到 1940 年代》, p. 115。
- 在某些情况下(异常色散),相速度可以超过 \(c\),但 “信号速度” 仍将小于或等于 \(c\)。
- 在某些书籍中,例如 U. Krey 和 A. Owen 的《基础理论物理》(Springer 2007),“有效电荷” 一词代替了
- “总电荷”,而 “自由电荷” 则被简单称为 “电荷”。 关于磁单极子的搜索,请参阅 “磁单极子”。最近,科学家们发现了一些类型的凝聚态物质,包括自旋冰和拓扑绝缘体,表现出类似于磁单极子的行为(参见 sciencemag.org 和 nature.com)。尽管这些在大众媒体中被描述为期待已久的磁单极子发现,但它们只是表面上相关。真正的磁单极子是指 \(\nabla \cdot B \neq 0\),而在这些凝聚态系统中,\(\nabla \cdot B = 0\),只有 \(\nabla \cdot H \neq 0\)。
17. 参考文献
- Hampshire, Damian P. (2018 年 10 月 29 日). "使用赫维赛德符号推导麦克斯韦方程". 《英国皇家学会哲学会刊 A:数学、物理和工程科学》, 376 (2134). arXiv:1510.04309. Bibcode:2018RSPTA.37670447H. doi:10.1098/rsta.2017.0447. ISSN 1364-503X. PMC 6232579. PMID 30373937.
- "2022 年 CODATA 值:真空中的光速". 常数、单位和不确定性参考. NIST. 2024 年 5 月. 取自 2024-05-18.
- Jackson, John. "麦克斯韦方程". 科学视频词汇. 伯克利实验室. 于 2019-01-29 存档. 取自 2016-06-04.
- J. D. Jackson, 《经典电动力学》, 第 6.3 节
- 《物理学原理:基于微积分的教材》, R. A. Serway, J. W. Jewett 著, 第 809 页。
- Bruce J. Hunt (1991),《麦克斯韦派》,第 5 章和附录,康奈尔大学出版社。
- "麦克斯韦方程",《工程与技术历史百科》,2019 年 10 月 29 日。取自 2021-12-04。
- Šolín, Pavel (2006),《偏微分方程与有限元方法》,约翰·威立公司,第 273 页。ISBN 978-0-471-72070-6。
- J. D. Jackson (1975 年 10 月 17 日),《经典电动力学》(第 3 版),威立出版社。ISBN 978-0-471-43132-9。
- Littlejohn, Robert (2007 年秋季),《电磁理论中的高斯、SI 及其他单位制》(PDF),加州大学伯克利分校物理 221A 课程讲义。取自 2008-05-06。
- David J Griffiths (1999),《电动力学导论》(第三版),普伦蒂斯霍尔出版社,第 559-562 页。ISBN 978-0-13-805326-0。
- Kimball Milton; J. Schwinger (2006 年 6 月 18 日),《电磁辐射:变分方法、波导和加速器》,施普林格科学与商业媒体出版社。ISBN 978-3-540-29306-4。
- 参见 David J. Griffiths (1999). "4.2.2". 《电动力学导论》(第三版),普伦蒂斯霍尔出版社,ISBN 9780138053260,以获取关于极化强度 \(P\) 与束缚电荷关系的良好描述。
- 参见 David J. Griffiths (1999). "6.2.2". 《电动力学导论》(第三版),普伦蒂斯霍尔出版社,ISBN 9780138053260,以获取关于磁化强度 \(M\) 与束缚电流关系的良好描述。
- Andrew Zangwill (2013),《现代电动力学》,剑桥大学出版社,ISBN 978-0-521-89697-9。
- Kittel, Charles (2005),《固体物理学导论》(第 8 版),美国:约翰·威立公司,ISBN 978-0-471-41526-8。
- Jack, P. M. (2003),《作为四元数结构的物理空间 I:麦克斯韦方程。简短笔记》,arXiv:math-ph/0307038。
- A. Waser (2000),《关于麦克斯韦场方程的符号表示》(PDF),AW-Verlag。
- Peter Monk (2003),《麦克斯韦方程的有限元方法》,英国牛津:牛津大学出版社,第 1 页起,ISBN 978-0-19-850888-5。
- Thomas B. A. Senior & John Leonidas Volakis (1995 年 3 月 1 日),《电磁学中的近似边界条件》,英国伦敦:电气工程师学会,第 261 页起,ISBN 978-0-85296-849-9。
- T Hagstrom (Björn Engquist & Gregory A. Kriegsmann 编辑) (1997),《计算波传播》,柏林:施普林格出版社,第 1 页起,ISBN 978-0-387-94874-4。
- Henning F. Harmuth & Malek G. M. Hussain (1994),《电磁信号的传播》,新加坡:世界科学出版社,第 17 页,ISBN 978-981-02-1689-4。
- David M Cook (2002),《电磁场理论》,美国纽约州米尼奥拉:柯瑞尔·多佛出版公司,第 335 页起,ISBN 978-0-486-42567-2。
- Jean-Michel Lourtioz (2005 年 5 月 23 日),《光子晶体:走向纳米级光子器件》,柏林:施普林格出版社,第 84 页,ISBN 978-3-540-24431-8。
- S. G. Johnson,《完美匹配层笔记》,麻省理工学院在线课程笔记(2007 年 8 月)。
- S. F. Mahmoud (1991),《电磁波导:理论与应用》,英国伦敦:电气工程师学会,第 2 章,ISBN 978-0-86341-232-5。
- John Leonidas Volakis, Arindam Chatterjee & Leo C. Kempel (1998),《电磁学的有限元方法:天线、微波电路与散射应用》,纽约:Wiley IEEE,第 79 页起,ISBN 978-0-7803-3425-0。
- Bernard Friedman (1990),《应用数学的原理与技术》,纽约州米尼奥拉:多佛出版公司,ISBN 978-0-486-66444-6。
- Taflove A & Hagness S C (2005),《计算电动力学:有限差分时域法》,波士顿马萨诸塞州:Artech House,第 6 章和第 7 章,ISBN 978-1-58053-832-9。
- H Freistühler & G Warnecke (2001),《双曲问题:理论、数值方法、应用》,施普林格出版社,第 605 页,ISBN 9783764367107。
- J Rosen (1980),“电磁场和势的冗余与多余性”,《美国物理学杂志》,48 (12): 1071。Bibcode:1980AmJPh..48.1071R。doi:10.1119/1.12289。
- J. A. Stratton (1941),《电磁理论》,麦格劳-希尔图书公司,第 1-6 页,ISBN 9780470131534。
- B Jiang, J Wu & L. A. Povinelli (1996),“计算电磁学中伪解的起源”,《计算物理学杂志》,125 (1): 104。Bibcode:1996JCoPh.125..104J。doi:10.1006/jcph.1996.0082。hdl:2060/19950021305。
- Weinberg, Steven (1972),《引力与宇宙学》,约翰·威立公司,第 161-162 页,ISBN 978-0-471-92567-5。
- Courant, R. & Hilbert, D. (1962),《数学物理方法:偏微分方程》,第 II 卷,纽约:Wiley-Interscience,第 15-18 页,ISBN 9783527617241。
18. 进一步阅读
- Imaeda, K. (1995), “麦克斯韦方程的双四元数形式及其解”,收录于 Ablamowicz, Rafał; Lounesto, Pertti(编辑),《克利福德代数与旋量结构》,施普林格出版社,第 265–280 页,doi:10.1007/978-94-015-8422-7_16,ISBN 978-90-481-4525-6。
历史文献
- 《关于法拉第力线》 – 1855/56 年。麦克斯韦的第一篇论文(第 1 和 2 部分)– 由 Blaze Labs Research 整理(PDF)。
- 《关于物理力线》 – 1861 年。麦克斯韦 1861 年关于磁力线的论文 – 1873 年《论文集》的前身。
- 詹姆斯·克拉克·麦克斯韦,“电磁场的动力理论”,《伦敦皇家学会哲学会刊》155, 459–512 (1865)。(此文与 1864 年 12 月 8 日麦克斯韦在皇家学会的演讲一同发表)。
- 《电磁场的动力理论》 – 1865 年。麦克斯韦 1865 年描述其 20 个方程的论文,链接来自 Google Books。
- J. Clerk Maxwell (1873),《电学与磁学论》:
- Maxwell, J. C., 《电学与磁学论》 – 第 1 卷 – 1873 年 – 卡内基梅隆大学 Posner 纪念馆藏。
- Maxwell, J. C., 《电学与磁学论》 – 第 2 卷 – 1873 年 – 卡内基梅隆大学 Posner 纪念馆藏。
相对论理论提出之前的发展
- Larmor, Joseph (1897),“关于电与发光介质的动力学理论. 第 3 部分,与物质介质的关系”,《英国皇家学会哲学会刊》,190: 205–300。
- Lorentz, Hendrik (1899),“在运动系统中电和光现象的简化理论”,《阿姆斯特丹科学院会议录》,I: 427–443。
- Lorentz, Hendrik (1904),“在任何速度低于光速的系统中的电磁现象”,《阿姆斯特丹科学院会议录》,IV: 669–678。
- Henri Poincaré (1900),“洛伦兹理论与反作用原理”(法文),《荷兰档案》,V, 253–278。
- Henri Poincaré (1902),《科学与假设》(法文)。
- Henri Poincaré (1905),“关于电子动力学”(法文),《法兰西科学院报告》,140, 1504–1508。
- Catt, Walton 和 Davidson. “位移电流的历史”,1979 年 3 月《无线电世界》,于 2008 年 5 月 6 日存档于 Wayback Machine。
19. 外部链接
- [“麦克斯韦方程”](https://www.encyclopediaofmath.org),《数学百科全书》,EMS 出版社,2001 [1994]
- [maxwells-equations.com](http://www.maxwells-equations.com) — 麦克斯韦方程的直观教程。
- [费曼物理学讲义 卷 II 第 18 章:麦克斯韦方程](http://www.feynmanlectures.caltech.edu)
- [Wikiversity 上的麦克斯韦方程页面](https://en.wikiversity.org/wiki/Maxwell
现代研究
- 《电磁学》(第 11 章),B. Crowell,全尔顿学院
- 讲座系列:相对论与电磁学,R. Fitzpatrick,德克萨斯大学奥斯汀分校
- Project PHYSNET 上的麦克斯韦方程推导出的电磁波
- 麻省理工学院视频讲座系列(36 个 50 分钟讲座)(.mp4 格式)– 电学与磁学,由沃尔特·莱温教授授课
其他
- Silagadze, Z. K. (2002),“费曼对麦克斯韦方程的推导与额外维度”,《路易斯·德布罗意基金会年刊》,27: 241–256。arXiv:hep-ph/0106235。
- 自然里程碑:光子 – 里程碑 2(1861)麦克斯韦方程