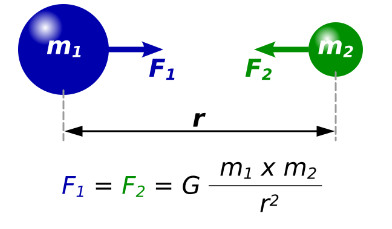牛顿万有引力定律（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 牛顿的万有引力定律指出，宇宙中的每一个粒子都以一种力吸引着其他粒子，这种力与它们质量的乘积成正比，与它们中心之间距离的平方成反比。相隔的物体互相吸引，就好像它们的所有质量都集中在它们的中心一样。该定律的发表被称为 “第一次伟大统一”，因为它标志着地球上重力现象与已知的天文行为的统一。[1][2][3]

　　 这是一个从经验观察中通过艾萨克·牛顿所称的归纳推理得出的普遍物理定律。[4] 它是经典力学的一部分，最早由牛顿在其著作《自然哲学的数学原理》（简称《原理》）中提出，该书首次出版于 1687 年 7 月 5 日。

　　 因此，万有引力的方程形式为： \[ F = G \frac{{m_1 m_2}}{{r^2}}~ \] 其中，\( F \) 是作用在两个物体之间的引力，\( m_1 \) 和 \( m_2 \) 是两个物体的质量，\( r \) 是它们质心之间的距离，\( G \) 是引力常数。

　　 对牛顿万有引力定律的首次实验室测试是由英国科学家亨利·卡文迪许在 1798 年进行的卡文迪许实验。[5] 这次实验发生在牛顿的《原理》发表 111 年后，大约在他去世 71 年后。

　　 牛顿的引力定律与库仑的电力定律相似，后者用于计算两个带电体之间产生的电力的大小。它们都是平方反比定律，即力与两个物体之间距离的平方成反比。库仑定律中用电荷代替质量，并使用不同的常数。

　　 牛顿的引力定律后来被阿尔伯特·爱因斯坦的广义相对论所取代，但引力常数的普适性依然存在，而且该定律在大多数应用中仍被用作计算引力效应的极好近似。只有在需要极高精度时，或在处理非常强的引力场（如在极其巨大和密集的物体附近）或小距离（例如水星绕太阳的轨道）时，才需要使用相对论。

1. 历史

　　 大约在 1600 年，科学方法开始扎根。勒内·笛卡尔从一个更基础的视角重新出发，发展了独立于神学的物质和作用的观念。伽利略·伽利莱写下了关于自由落体和滚动物体的实验测量的著作。约翰内斯·开普勒的行星运动定律总结了第谷·布拉赫的天文观测。[6]: 132

　　 大约在 1666 年，艾萨克·牛顿提出了开普勒定律也必须适用于月亮围绕地球的轨道，进而适用于地球上的所有物体的想法。该分析需要假设引力作用如同地球的所有质量集中在其中心一样，这是当时未经证实的猜想。他对月球轨道周期的计算值与已知值相差 16%。到 1680 年，地球直径的新测量值使他的轨道周期计算值与已知值相差缩小至 1.6%，更重要的是，牛顿找到了对他之前猜想的证明。[7]: 201

　　 1687 年，牛顿发表了他的《自然哲学的数学原理》（Principia），将他的运动定律与新的数学分析相结合，解释了开普勒的经验结果。[6]: 134 他的解释形式是一条万有引力定律：任何两个物体之间的吸引力与它们的质量成正比，与它们的距离平方成反比。[8]: 28 牛顿的原始公式为： \[ \text{重力} \propto \frac{\text{物体 1 的质量} \times \text{物体 2 的质量}}{\text{中心间距离}^2}~ \] 其中符号 ∝ 表示 “成比例”。要将其转化为一个等式，需要一个乘数或常数，以在任何质量值或距离下给出正确的引力大小（即引力常数）。牛顿需要准确测量这个常数以证明他的平方反比定律。当牛顿在 1686 年 4 月向皇家学会提交尚未出版的《自然哲学的数学原理》第一卷时，罗伯特·胡克声称牛顿是从他那里获得了平方反比定律，最终被认为是无稽之谈。[7]: 204

牛顿 “至今未知的原因”

　　 虽然牛顿在他的巨著中成功地阐述了引力定律，但他对方程式暗示的 “超距作用” 概念深感不安。1692 年，在写给本特利的第三封信中，他写道：“一个物体可以通过真空对另一个物体施加作用，而无需任何其他物质来传递它们之间的作用力，这对我来说是极其荒谬的。我相信，没有哪个在哲学问题上有合格思维能力的人会落入这种荒谬中。”

　　 他从未 “指明这种力量的原因”。在所有其他情况下，他利用运动现象来解释作用于物体的各种力的起源，但在引力的情况下，他无法通过实验识别产生引力的运动（尽管他在 1675 年和 1717 年提出了两种机械假说）。此外，他甚至拒绝就这种力的原因提出假设，因为他认为这违背了严谨的科学。他感叹道，“哲学家们迄今为止徒劳地尝试在自然中寻找” 引力的源头，因为他 “通过许多理由” 确信存在 “至今未知的原因”，这些原因是所有 “自然现象” 的基础。这些基本现象至今仍在研究之中，尽管假说层出不穷，但尚未找到最终的答案。而在牛顿 1713 年《自然哲学的数学原理》第二版的总注中，他写道：“我至今未能从现象中发现这些引力性质的原因，我不编造假说……重力确实存在并按照我所解释的定律作用，这已足以解释所有天体的运动。”[9]

2. 现代形式

　　 用现代语言表述，这一定律如下： 每个点质量通过沿两点连线的作用力吸引每一个其他点质量。该力与两个质量的乘积成正比，与它们之间距离的平方成反比：[10]

图
图 1

　　 \[ F = G \frac{m_1 m_2}{r^2}~ \] 其中：

　　 假设使用国际单位制，\( F \) 的单位为牛顿（N），\( m_1 \) 和 \( m_2 \) 的单位为千克（kg），\( r \) 的单位为米（m），引力常数 \( G \) 的值为 \( 6.67430(15) \times 10^{-11} \, \text{m}^3 \cdot \text{kg}^{-1} \cdot \text{s}^{-2} \)。[11] 该常数 \( G \) 的数值首次由英国科学家亨利·卡文迪什在 1798 年通过卡文迪什实验精确测定，尽管卡文迪什本人并未计算出 \( G \) 的数值。[5] 该实验也是首次在实验室中测试牛顿万有引力理论的实验。它发生在牛顿《自然哲学的数学原理》发表后 111 年以及牛顿去世 71 年之后，因此牛顿的计算中并未使用 \( G \) 的数值；相反，他只能计算相对于另一种力的力。

图
图 2：误差图显示了引力常数 \( G \) 的实验值。

3. 具有空间范围的物体

图
图 3：地球内部的引力场强

　　 如果所讨论的物体具有空间范围（而非点质量），那么它们之间的引力是通过对构成这些物体的假想点质量的贡献进行求和来计算的。在极限情况下，当组成的点质量变得‘无限小’时，这就需要在两个物体的范围内对力（以矢量形式，见下文）进行积分。

　　 通过这种方式，可以证明具有球对称质量分布的物体对外部物体施加的引力与其所有质量集中在中心点时的引力相同。[10]（这一结论对于非球对称的物体通常并不成立。）

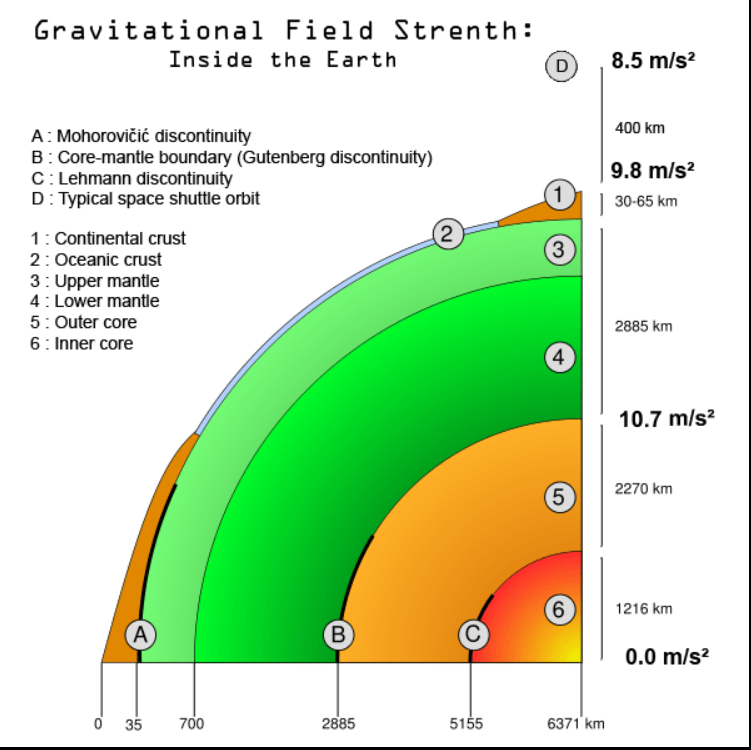
　　 对于位于球对称质量分布内部的点，可以使用牛顿的壳层定理来找到引力。该定理告诉我们，质量分布的不同部分如何影响位于距质量分布中心距离为 \( r_0 \) 的点上测量的引力：[12]

　　 因此，例如，在一个均匀厚度和密度的球壳内部，空心球体内的任何位置都不会有净引力加速度。

图
图 4：地球表面附近的重力场——物体朝地表加速运动

4. 矢量形式

图
图 5：从宏观角度看环绕地球的引力场。

　　 牛顿的万有引力定律可以写成一个矢量方程，以同时考虑引力的方向和大小。在这个公式中，加粗的量表示矢量。 \[ \mathbf{F}_{21} = -G \frac{m_1 m_2}{|\mathbf{r}_{21}|^2} \hat{\mathbf{r}}_{21} = -G \frac{m_1 m_2}{|\mathbf{r}_{21}|^3} \mathbf{r}_{21}~ \] 其中：

　　 可以看出，该方程的矢量形式与之前给出的标量形式相同，只是现在力 \(\mathbf{F}\) 是一个矢量量，并且右侧乘上了相应的单位矢量。此外，也可以看到 \(\mathbf{F}_{12} = -\mathbf{F}_{21}\)。

5. 重力场

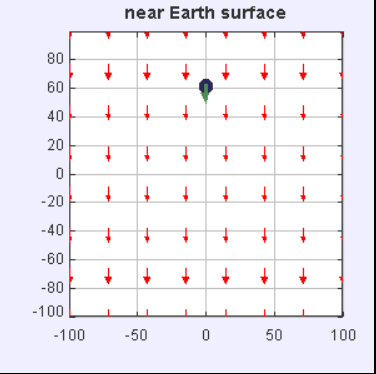
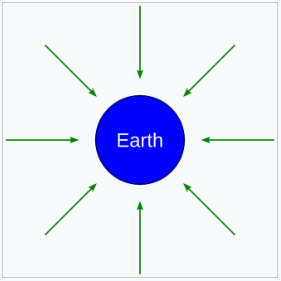
　　 重力场是一个矢量场，用于描述在空间任意给定点上施加在物体上的单位质量重力。实际上，它等于该点的重力加速度。

　　 这是矢量形式的推广，在涉及两个以上的物体时尤其有用（例如在地球和月球之间的火箭）。对于两个物体（例如物体 2 是火箭，物体 1 是地球），我们可以用 \( r \) 代替 \( r_{12} \)，用 \( m \) 代替 \( m_2 \)，并定义重力场 \( g(r) \) 为： \[ \mathbf {g} (\mathbf {r} )=-G{m_{1} \over {{\vert \mathbf {r} \vert }^{2}}}\,\mathbf {\hat {r}}~ \] 因此我们可以写成： \[ \mathbf {F} (\mathbf {r} )=m\mathbf {g} (\mathbf {r} ).~ \] 这个公式依赖于产生该场的物体。该场的单位是加速度；在国际单位制（SI）中，这是 \( \text{m/s}^2 \)。

　　 重力场也是保守的；即从一个位置到另一个位置所做的重力功与路径无关。这导致存在一个重力势场 \( V(r) \) 使得 \[ \mathbf {g} (\mathbf {r} )=-\nabla V(\mathbf {r} ).~ \] 如果 \( m_1 \) 是一个点质量或具有均匀质量分布的球体的质量，则球体外的力场 \( g(r) \) 是各向同性的，即仅依赖于距球体中心的距离 \( r \)。在这种情况下： \[ V(r) = -G \frac{m_1}{r}.~ \] 根据高斯定律，对称体内的场可以通过以下数学公式找到： \[ \iint_{\partial V} \mathbf{g(r)} \cdot d\mathbf{A} = -4 \pi G M_{\text{enc}},~ \] 其中 \( \partial V \) 是一个封闭曲面，\( M_{\text{enc}} \) 是该曲面内封闭的质量。

　　 因此，对于半径为 \( R \) 且总质量为 \( M \) 的空心球体， \[ |\mathbf{g(r)}| = \begin{cases} 0, & \text{if } r < R \\ \frac{GM}{r^2}, & \text{if } r \geq R \end{cases}~ \] 对于半径为 \( R \) 且总质量为 \( M \) 的均匀实心球体， \[ |\mathbf{g(r)}| = \begin{cases} \frac{GMr}{R^3}, & \text{if } r < R \\ \frac{GM}{r^2}, & \text{if } r \geq R \end{cases}~ \]

6. 局限性

　　 牛顿的重力描述在许多实际应用中足够准确，因此被广泛使用。当无量纲量 \(\frac{\phi}{c^2}\) 和 \(\left(\frac{v}{c}\right)^2\) 都远小于 1 时，与其偏差很小。其中，\(\phi\) 是引力势，\(v\) 是研究对象的速度，\(c\) 是真空中的光速。例如，牛顿重力对地球/太阳系统的描述非常准确，因为 \[ \frac{\phi}{c^2} = \frac{GM_{\text{sun}}}{r_{\text{orbit}} c^2} \sim 10^{-8}, \quad \left(\frac{v_{\text{Earth}}}{c}\right)^2 = \left(\frac{2 \pi r_{\text{orbit}}}{(1\ \text{yr}) c}\right)^2 \sim 10^{-8},~ \] 其中 \(r_{\text{orbit}}\) 是地球绕太阳的轨道半径。

　　 在无量纲参数较大的情况下，必须使用广义相对论来描述系统。当引力势较小且速度较低时，广义相对论会简化为牛顿重力。因此，牛顿引力定律通常被认为是广义相对论的低引力极限。

与牛顿公式冲突的观测结果

爱因斯坦的解答

　　 上述与观测不符的前两点被爱因斯坦的广义相对论所解释。在广义相对论中，引力是曲率时空的表现，而非由物体之间传播的力所致。在爱因斯坦的理论中，能量和动量会使其周围的时空发生扭曲，其他粒子沿由时空几何决定的轨迹运动。这种描述使得光和物质的运动可以与所有现有的观测结果相一致。在广义相对论中，引力被视为一种虚拟力，它源于时空的曲率，因为自由落体物体的引力加速度是由于其世界线是时空中的测地线。

7. 扩展

　　 近年来，通过中子干涉实验，人们开始探寻引力定律中非平方反比项的可能性。

8. 牛顿万有引力定律的解法

　　 n 体问题是一个古老的经典问题，涉及预测一组相互之间通过引力作用的天体的个体运动。自古希腊时期起，解决这一问题的动机便是为了理解太阳、行星和可见恒星的运动。在 20 世纪，理解球状星团系统的动力学也成为了一个重要的 n 体问题。n 体问题在广义相对论中则更为难以求解。

　　 这个经典物理问题可以非正式地描述为：给定一组天体的准稳定轨道属性（瞬时位置、速度和时间），预测它们之间的相互作用力；进而，预测它们在未来任意时刻的真实轨道运动。

　　 二体问题已经被完全解决，而限制性三体问题也已得到解决。

9. 另见

10. 参考文献

  1. Fritz Rohrlich (1989 年 8 月 25 日). 《从悖论到现实：我们对物理世界的基本概念》。剑桥大学出版社。第 28 页起。ISBN 978-0-521-37605-1。
  2. Klaus Mainzer (2013 年 12 月 2 日). 《自然对称性：自然哲学和科学手册》。Walter de Gruyter。第 8 页起。ISBN 978-3-11-088693-1。
  3. "物理学：基本力和理论的综合"。《Encyclopedia.com》。
  4. 艾萨克·牛顿："在[实验]哲学中，特殊命题是从现象中推导出来的，然后通过归纳被推广为一般性命题"：《自然哲学的数学原理》，卷 3，通论，第 392 页，安德鲁·莫特的 1729 年英文翻译第二卷。
  5. Laurent Hodges. "米歇尔–卡文迪许实验"。印第安纳州立大学。
  6. Mary B. Hesse (2005). 《力与场：物理学历史中的距离作用概念》。纽约州米尼奥拉：Dover 出版社。ISBN 978-0-486-44240-2。
  7. Feather, Norman (1959). 《质量、长度和时间物理学导论》。爱丁堡大学出版社。
  8. Whittaker, Edmund T. (1989). 《以太和电理论的历史》。卷 1：经典理论（重印版）。纽约：Dover 出版社。ISBN 978-0-486-26126-3。
  9. Westfall, Richard S. (1978). 《现代科学的建构：机制与力学》。剑桥大学出版社。
  10. 命题 75，定理 35：第 956 页 – I.Bernard Cohen 和 Anne Whitman 译：《艾萨克·牛顿，原理：自然哲学的数学原理》。由 I.Bernard Cohen 撰写的《牛顿原理指南》为序。加利福尼亚大学出版社，1999 年。ISBN 0-520-08816-6，ISBN 0-520-08817-4。
  11. "2022 CODATA 值：牛顿引力常数"。美国国家标准与技术研究院（NIST）参考常数、单位和不确定性页面。NIST。2024 年 5 月。访问于 2024 年 5 月 18 日。
  12. "旋转扁率"。farside.ph.utexas.edu。
  13. 矢量差 r2 − r1 指向物体 1 到物体 2。参见《费曼物理学讲义》第一卷，图 11–6，方程(9.19)，以及欧几里得矢量#加减法。
  14. Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). 《引力》。纽约：W. H. Freeman and Company。第 1049 页。ISBN 978-0-7167-0344-0。
  15. Born, Max (1924). 《爱因斯坦的相对论理论》（1962 年 Dover 版，第 348 页列出一张表格，记录了水星、金星和地球近日点进动的观测值和计算值）。
  16. Greene, Geoffrey L.; Gudkov, Vladimir (2007). “通过中子干涉法对纳米尺度非牛顿引力的改进约束”。《物理评论 C》，第 75 卷第 1 期：015501。arXiv:hep-ph/0608346。Bibcode:2007PhRvC..75a5501G。doi:10.1103/PhysRevC.75.015501。S2CID 39665455。
  17. Leimanis 和 Minorsky：我们关注的是 Leimanis，他首先讨论了 n 体问题的一些历史，特别是 Kovalevskaya 女士在 1868-1888 年间花费二十年进行的复变量方法尝试以及其失败；第 1 部分：刚体动力学与数学外弹道学（第 1 章，关于固定点的刚体运动（欧拉和泊松方程）；第 2 章，数学外弹道学），是 n 体问题的良好前奏背景；第 2 部分：天体力学（第 1 章，三体问题的统一化（受限三体问题）；第 2 章，三体问题中的捕获；第 3 章，广义 n 体问题）。
  18. 准稳态载荷是指由瞬时角速度和加速度以及平动加速度产生的瞬时惯性载荷（9 个变量）。这类似于拍摄了一张记录瞬时位置和运动属性的照片。相比之下，稳态条件是指系统状态对时间不变；否则，所有的导数包括一阶和更高阶导数都为零。
  19. R. M. Rosenberg 对 n 体问题的描述相似（参见参考文献）：“一个有限数量的粒子系统中的每个粒子都受到其他所有粒子的牛顿引力吸引，而不受其他力的作用。如果给定系统的初始状态，粒子将如何运动？” Rosenberg 和其他人一样未能意识到在确定运动之前必须首先确定力。
  20. 已知在第一积分的经典通解中，求解 n 体问题是不可能的。对于任意 n 的精确理论解可以通过泰勒级数近似，但实际上这种无穷级数必须被截断，最多只能得到一个近似解；而且这种方法现已过时。此外，n 体问题可以通过数值积分来解决，但这些也是近似解；同样也已过时。详见 Sverre J. Aarseth 的《引力 n 体模拟》一书（列在参考文献中）。

                     

© 小时科技 保留一切权利