傅里叶变换的数值计算、快速傅里叶变换(Matlab)
贡献者: addis
1. 直接数值积分
作为下文 FFT 方法的参照,我们先实现直接用数值积分计算傅里叶变换(式 1 )。调用时需要提供一元函数(句柄)f,而不是一系列离散函数值。xspan 是对 f 积分的区间,而 kspan 是输出中 k 的区间,Nk 是 k 的长度。这么做虽然直观且精确,但计算量较大,所以一般还是用下一节中的 FFT 方法。
尤其是如果 f 并不是通过函数给出,而只是一系列等间距的散点,那么与其先插值再做数值积分,FFT 方法是最适合的,因为 FFT 已经相当于对散点进行了 sinc 插值(子节 4 )。
代码 1:CFT.m
% Continuous Fourier Transform by Integration
% f must be a function handle
% gh is function handle, g = gh(linspace(kmin,kmax,Nk))
% input the 7th argument to plot spectrum
function [k,g,gh] = CFT(f,xspan,kspan,Nk,~)
k = linspace(kspan(1),kspan(2),Nk);
g = zeros(1,Nk);
for ii = 1:Nk
integrand = @(x) f(x).*exp(-1i*k(ii)*x);
g(ii) = integral(integrand,xspan(1),xspan(2), 'AbsTol',1e-8);
end
g = g/sqrt(2*pi);
if nargin == 5
figure; plot(k,g);
end
if nargout == 3
gh = @(kq) interp1(k,g,kq,'spline');
end
end
代码 2:iCFT.m
% Continuous Fourier Transform by Integration
% g must be a function handle
% fh is function handle, f = fh(linspace(xmin,xmax,Nx))
% input the 7th argument to plot spectrum
function [x,f,fh] = iCFT(g,kspan,xspan,Nx,~)
x = linspace(xspan(1),xspan(2),Nx);
f = zeros(1,Nx);
for ii = 1:Nx
integrand = @(k) g(k).*exp(1i*k*x(ii));
f(ii) = integral(integrand,kspan(1),kspan(2), 'AbsTol',1e-8);
end
f = f/sqrt(2*pi);
if nargin == 5
figure; plot(x,f);
end
if nargout == 3
fh = @(xq) interp1(x,f,xq,'spline');
end
end
2. 用 FFT 近似傅里叶变换
这里使用的算法见子节 7 。给出任意等间距的 $x$ 坐标格点 [x0, x0+dx, x0+2*dx, ...],以及对应的函数值 f = [f(1), f(2), ...],那么该代码可以通过 Matlab 提供的快速傅里叶变换(FFT)计算傅里叶变换(式 1 )。输入中 Nk 是可选的,默认等于 x 的个数。若 Nk 大于 f 的个数,输出中 k 的步长将会相应变小使 k 的长度为 Nk,但区间不会变。k 的区间是由 dx 决定的。在实现上,当 Nk > numel(f) 时会预先在 f 两边添加 0 使其先具有 Nk 个元。
代码 3:FFT.m
% fft approximation of the analytical fourier transform from f(x) to g(k)
% x and k are both equally spaced, x starts from x0 equally spaced by dx
% norm(g) = norm(f)
% numel(g) = Nk
function [g, k] = FFT(f, x0, dx, Nk, k_mid)
N = numel(f);
if ~isvector(f)
error('f must be a vector!');
end
if ~exist('k_mid', 'var')
k_mid = 0;
end
if ~exist('Nk', 'var')
Nk = N;
end
f = reshape(f, 1, N);
x_mid = x0 + ceil((N-1)/2)*dx;
if k_mid ~= 0
x = linspace(x0, x0+dx*(N-1), N);
f = f .* exp(-1i*k_mid*(x-x_mid));
end
if Nk > N
N = Nk;
f = fftresize(f, N);
end
g = sffts(f)*(dx/sqrt(2*pi));
k = fftlinspace(2*pi/dx, N) + k_mid;
if (abs(x_mid/x0) > 2*eps)
g = g .* exp(-1i*k*x_mid);
end
end
代码 4:iFFT.m
% ifft approximation of the analytical inverse Fourier transform
% from g(k) to f(x)
% x and k are both equally spaced, k starts from k0 equally spaced by dk
% norm(g) = norm(f)
% numel(f) = Nx
function [f, x] = iFFT(g, k0, dk, Nx, x_mid)
N = numel(g);
if ~isvector(g)
error('g must be a vector!');
end
if ~exist('x_mid', 'var')
x_mid = 0;
end
if ~exist('Nx', 'var')
Nx = N;
end
g = reshape(g, 1, N);
k_mid = k0 + ceil((N-1)/2)*dk;
if x_mid ~= 0
k = linspace(k0, k0+dk*(N-1), N);
g = g .* exp(1i*x_mid*k);
end
if Nx > N
N = Nx;
g = fftresize(g, N);
end
f = siffts(g)*(N*dk/sqrt(2*pi));
x = fftlinspace(2*pi/dk, N) + x_mid;
if (abs(k_mid/k0) > 2*eps)
f = f .* exp(1i*k_mid*(x-x_mid));
end
end
下面是一些依赖程序
代码 5:fftresize.m
% resize vector/matrix length for ftt by zero padding on both ends
function y = fftresize(x, newN)
% === x is row vector ===
if size(x, 1) == 1
N = numel(x);
Ndiff = abs(newN - N);
if newN > N % 0-padding
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = [zeros(1, Ndiff), x, zeros(1, Ndiff)];
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = [zeros(1, Ndiff), x, zeros(1, Ndiff+1)];
else
y = [zeros(1, Ndiff+1), x, zeros(1, Ndiff)];
end
end
elseif newN < N % shrink
y = shrink(x, N, Ndiff);
else
y = x;
end
% === x is column vector ===
elseif size(x, 2) == 1
N = numel(x);
Ndiff = abs(newN - N);
if newN > N % 0-padding
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = [zeros(Ndiff, 1); x; zeros(Ndiff, 1)];
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = [zeros(Ndiff, 1); x; zeros(Ndiff+1, 1)];
else
y = [zeros(Ndiff+1, 1); x; zeros(Ndiff, 1)];
end
end
elseif newN < N % shrink
y = shrink(x, N, Ndiff);
else
y = x;
end
% === x is matrix ===
else
[N, Ncol] = size(x);
Ndiff = abs(newN - N);
if newN > N % 0-padding
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = [zeros(Ndiff, Ncol); x; zeros(Ndiff, Ncol)];
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = [zeros(Ndiff, Ncol); x; zeros(Ndiff+1, Ncol)];
else
y = [zeros(Ndiff+1, Ncol); x; zeros(Ndiff, Ncol)];
end
end
elseif newN < N % shrink
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = x(Ndiff+1:end-Ndiff, :);
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = x(Ndiff+2:end-Ndiff, :);
else
y = x(Ndiff+1:end-Ndiff-1, :);
end
end
else
y = x;
end
end
end
function y = shrink(x, N, Ndiff)
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = x(Ndiff+1:end-Ndiff);
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = x(Ndiff+2:end-Ndiff);
else
y = x(Ndiff+1:end-Ndiff-1);
end
end
end
代码 6:sffts.m
% shifted fft
function y = sffts(x, dim)
if nargin < 2
y = fftshift(fft(ifftshift(x)));
else
y = fftshift(fft(ifftshift(x, dim),[], dim), dim);
end
end
代码 7:fftlinspace.m
% generate N grid points from bandwidth
% input 2 or 3 arguments
function x = fftlinspace(L, N, x0)
if mod(N, 2) == 0
Lh = 0.5*L; dx = L/N;
if nargin == 3
x = linspace(-Lh+x0, Lh-dx+x0, N);
else
x = linspace(-Lh, Lh-dx, N);
end
else
a = (N-1)*L/(2*N);
if nargin == 3
x = linspace(-a+x0, a+x0, N);
else
x = linspace(-a, a, N);
end
end
end
示例
% === params ===
x0 = -6; dx = 0.05; N = 300;
Nk = 4*N; k_mid = 0.25;
a = 2; x_shift = 0.8; k_shift = 2;
f_anal = @(x) exp(-a*(x-x_shift).^2) .* exp(1i*k_shift*(x-x_shift));
g_anal = @(k) exp(-(k-k_shift).^2/(4*a))/sqrt(2*a) .* exp(-1i*x_shift*k);
% =============
close all;
x = linspace(x0, x0+dx*(N-1), N).';
x_mid = x0 + ceil((N-1)/2)*dx;
[g, k] = FFT(f_anal(x), x0, dx, Nk, k_mid);
k = k(:); g = g(:);
k0 = k(1); dk = k(2)-k(1);
[f_, x_] = iFFT(g, k0, dk, N, x_mid);
f_ = f_(:); x_ = x_(:);
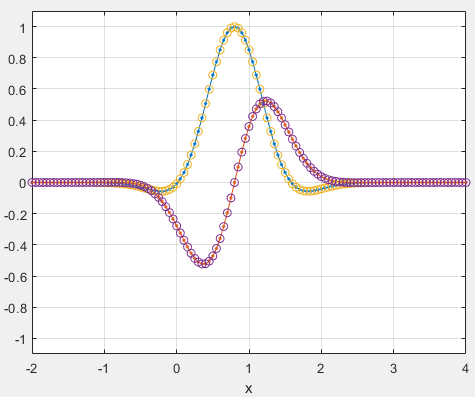
figure; plot(x, [real(f_anal(x)), imag(f_anal(x))], '.-');
hold on; plot(x_, [real(f_) imag(f_)], 'o');
grid on; axis([-2, 4, -1.1, 1.1]);
xlabel x;
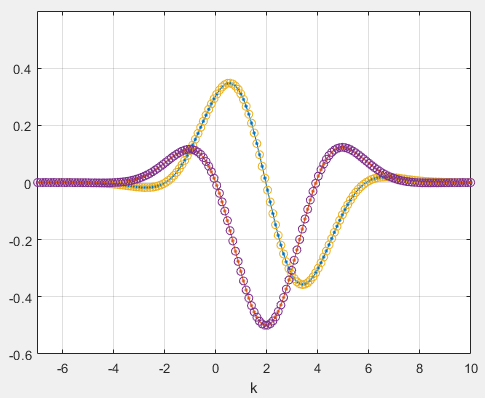
figure; plot(k, [real(g_anal(k)), imag(g_anal(k))], '.-');
hold on; plot(k, [real(g), imag(g)], 'o');
grid on; axis([-7, 10, -0.6, 0.6]);
xlabel k;
图 1:输出 $f(x)$
图 2:输出 $g(k)$
傅里叶级数
根据式 12 ,傅里叶级数与傅里叶变换值相差一个常数:
代码 8:FS.m
% Fourier series by FFT
function [C, k] = FS(f, x0, dx)
[g, k] = FFT(f, x0, dx, Nk, dim);
C = sqrt(2*pi)/(N*dx) * g;
end
3. sinc 插值
根据采样定理,可以使用 FFT 对函数的离散值进行 sinc 插值,dx 是可选的。
代码 9:fftinterp.m
% approximate sinc interpolation by fft
% N is optional, used to zero-pad f
function [f1, x1] = fftinterp(f, N1, dx, N)
if ~exist('N','var') || isempty(N)
N = numel(f);
else
f = fftresize(f, N);
end
f1 = siffts(fftresize(sffts(f), N1))*N1/N;
if nargout == 2
x1 = fftlinspace(dx*N, N1);
end
end
为了对比验证,我们也可以直接实现 sinc 插值,但该代码的效率较低
代码 10:sinc_interp.m
% sinc_interp
function y = sinc_interp(x, x0, y0)
N0 = numel(x0);
y = zeros(size(x));
dx0 = (max(x0)-min(x0))/(numel(x0)-1);
a = pi/dx0;
for ii = 1:N0
y = y + y0(ii).*sinc(a*(x-x0(ii)));
end
end
function y = sinc(x)
mask = (x~=0);
y(mask) = sin(x(mask))./x(mask);
y(~mask) = 1;
end