电偶极子辐射
贡献者: ACertainUser; addis
- 本文处于草稿阶段。
1令原点处的电偶极子为
\begin{equation}
\boldsymbol{\mathbf{p}} (t) = p_0 \cos\left(\omega t\right) \hat{\boldsymbol{\mathbf{z}}} ~.
\end{equation}
使用洛伦兹规范,在 $d \ll \lambda \ll r$ 的远场近似下($d$ 是偶极子的长度,$\lambda = \frac{2\pi}{k}$)
\begin{equation}
\varphi(r, \theta, t) = -\frac{p_0\omega}{4\pi\epsilon_0 c} \left(\frac{\cos\theta}{r} \right) \sin[\omega(t - r/c)]~,
\end{equation}
\begin{equation}
\boldsymbol{\mathbf{A}} (r, \theta, t) = -\frac{\mu_0 p_0 \omega}{4\pi r} \sin[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{z}}} ~.
\end{equation}
\begin{equation}
\boldsymbol{\mathbf{E}} = -\frac{\mu_0 p_0\omega^2}{4\pi} \left(\frac{\sin\theta}{r} \right) \cos[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{\theta}}} ~~,
\end{equation}
\begin{equation}
\boldsymbol{\mathbf{B}} = -\frac{\mu_0 p_0\omega^2}{4\pi c} \left(\frac{\sin\theta}{r} \right) \cos[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{\phi}}} ~.
\end{equation}
图 1:$Z=0$ 平面上的电场矢量场.原点附近由于远场近似不再有效而发散。笔者制作的一个可动的立体模型(站外链接)
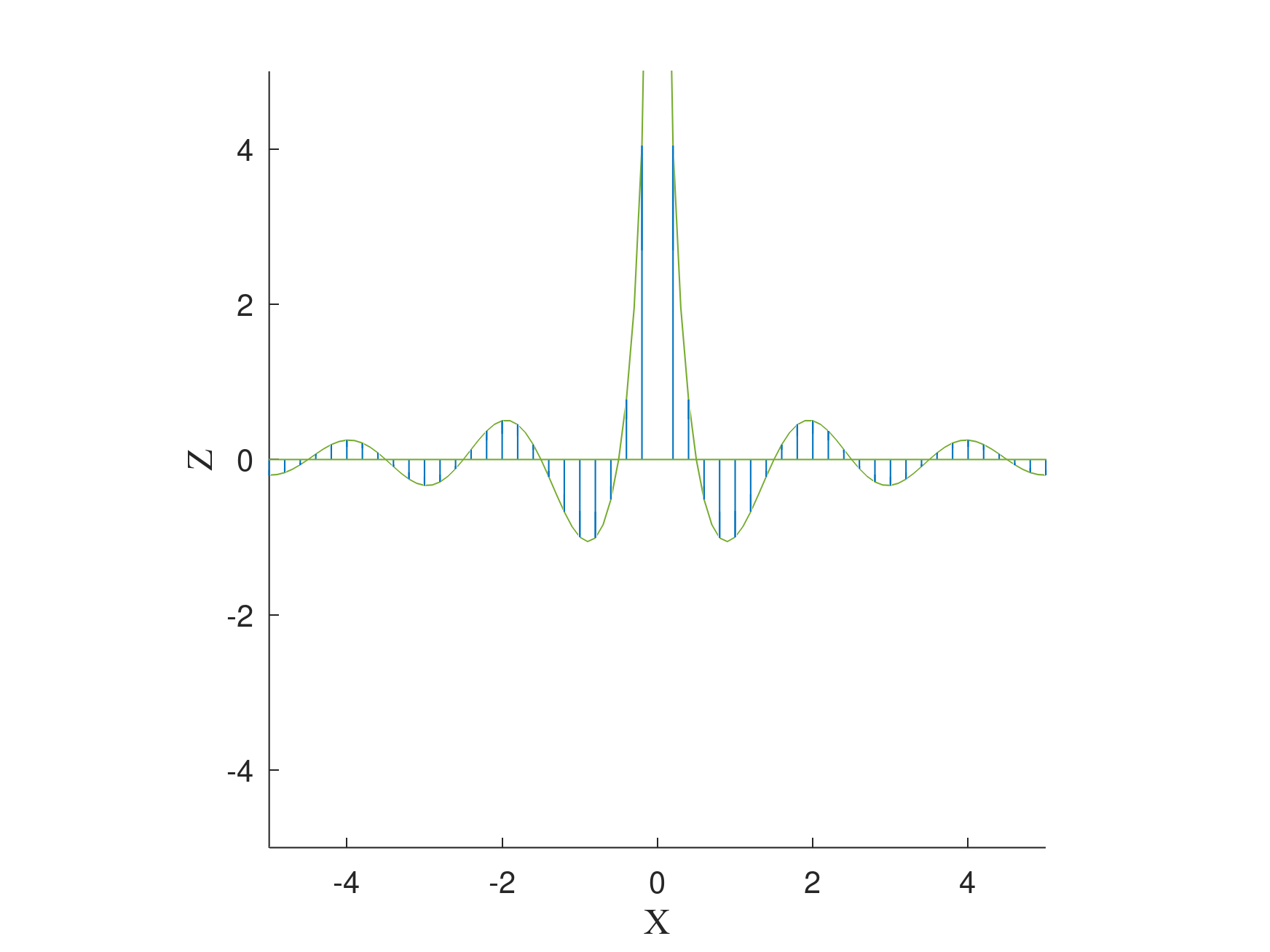
图 2:$X$ 轴上的电场矢量场。在远处辐射场行为类似平面电磁波
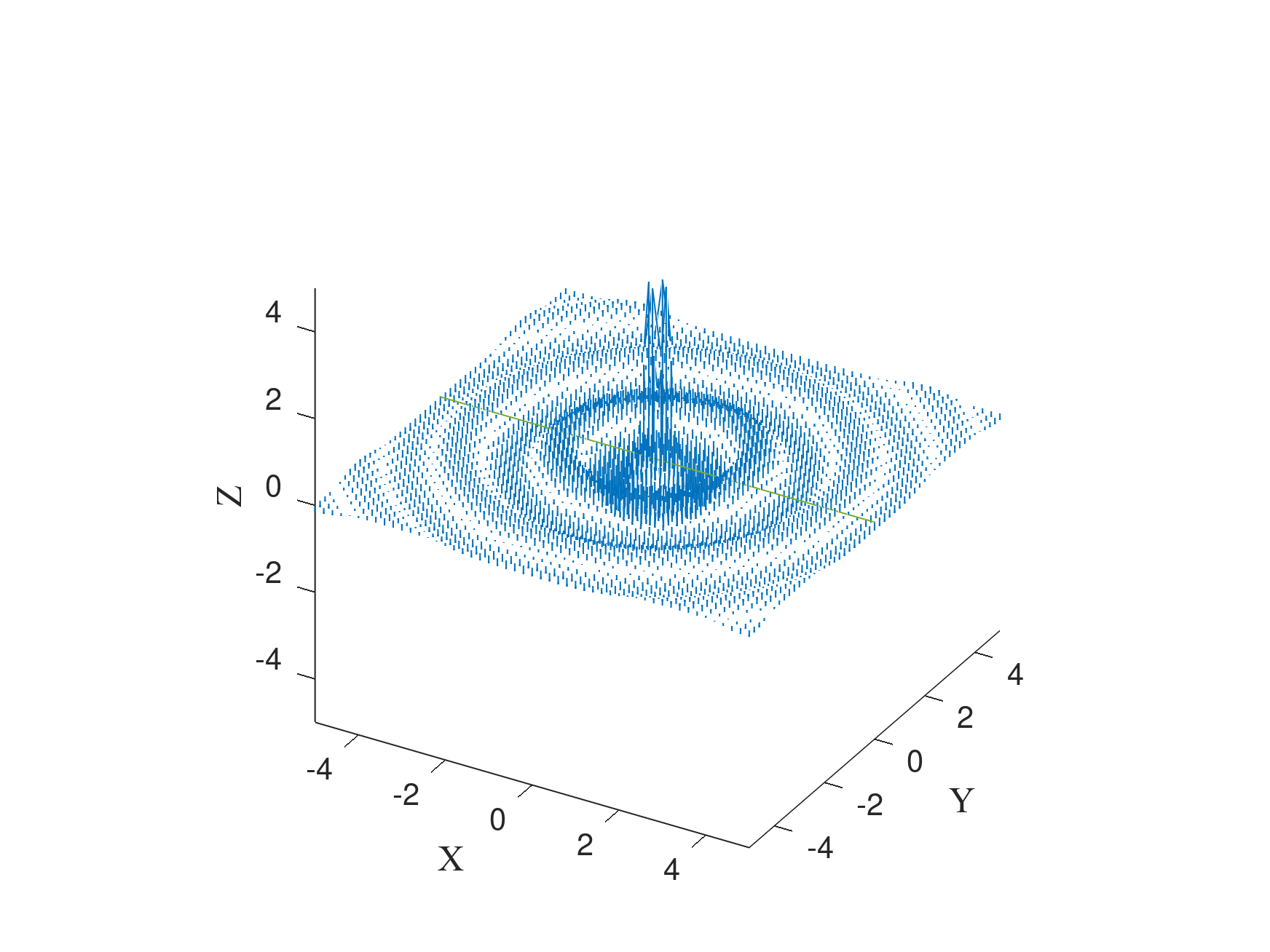
图 3:$Y=0$ 上的电场矢量场。
绘制矢量场的.m 代码
clc
clear
T=2;%周期
w=2*pi/T;
v=1;%波速
k=w/v;
t=0;%时刻
[x y z] = meshgrid(-5:0.2:5,-5:0.2:5,-5:0.2:5);
%将轴的范围设成0,可得到截面上的矢量场.完整的矢量场太复杂了
[phi theta r]=cart2sph(x,y,z);
theta = pi/2-theta;
E = -(sin(theta)./r).*cos(w*t-k*r);%电场强度数值
a = E.*cos(theta).*cos(phi);
b = E.*cos(theta).*sin(phi);
c = E.*-sin(theta);
hold on
axis equal;
axis([-5 5 -5 5 -5 5]);
xlabel('X','fontsize',12,'fontname','Times New Roman');
ylabel('Y','fontsize',12,'fontname','Times New Roman');
zlabel('Z','fontsize',12,'fontname','Times New Roman');
quiver3(x,y,z,a,b,c,0);
line([-10 10], [0 0],[0 0]);
hold off
辐射功率
可用能流密度(坡印廷矢量)描述辐射功率。
\begin{equation}
\boldsymbol{\mathbf{s}} ( \boldsymbol{\mathbf{r}} , t) = \frac{1}{\mu_0} \boldsymbol{\mathbf{E}} \boldsymbol\times \boldsymbol{\mathbf{B}} = \frac{\mu_0p_0^2\omega^4}{16\pi^2c} \frac{\sin^2\theta}{r^2} \cos^2[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{r}}} ~.
\end{equation}
\begin{equation}
\left\langle \boldsymbol{\mathbf{s}} \right\rangle = \frac{1}{\mu_0} \boldsymbol{\mathbf{E}} \boldsymbol\times \boldsymbol{\mathbf{B}}
= \frac{\mu_0p_0^2\omega^4}{32\pi^2c} \frac{\sin^2\theta}{r^2} \hat{\boldsymbol{\mathbf{r}}} ~.
\end{equation}
图 4:$ \left\langle \boldsymbol{\mathbf{s}} \right\rangle $ 的“等强度面”,内圈的 $ \left\langle \boldsymbol{\mathbf{s}} \right\rangle $ 强度更高.注意平行于偶极子的方向上没有能流.一个立体模型(站外链接)
总辐射功率(时间平均)为
\begin{equation}
\left\langle P \right\rangle = \oint \left\langle \boldsymbol{\mathbf{s}} \right\rangle \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{a}} } = \frac{\mu_0 p_0^2 \omega^4}{12\pi c}~.
\end{equation}
[1] ^ David Griffiths, Introduction to Electrodynamics, 4ed