最小二乘法拟合函数(Matlab)
贡献者: addis
我们在 “最小二乘法” 见到的三个例子中,方差函数都是待定系数的线性组合,这种情况下我们令偏导为零后得到的是线性方程组,便于求解。然而当方差不是待定系数的线性组合时,得到的方程组往往非常复杂,这时就需要借助数值计算。相比用数值计算解 $N$ 元的非线性方程组,更简单的方法是直接用数值方法寻找方差函数的极小值(如 Nelder-Mead 算法)。实践证明,大多数情况下极小值点仅有一个,那就是最小值点。
为了验证结果的正确性,我们先来用数值方法拟合 $A \cos\left(x + \varphi_0\right) + C$,并与 “最小二乘法” 中的方法比较结果。
图 1:运行结果
Matlab 代码如下,需要 NelderMead.m 函数:
代码 1:curveFit_test.m
function curveFit_test
close all;
% 随机生成简谐曲线
N = 20;
x0 = linspace(0, 2*pi, N);
y0 = 5*rand * sin(x0 + 2*pi * rand) + 10 * rand;
y0 = y0 + 2*rand(1,20); % 产生随机误差
scatter(x0, y0, '+'); % 画出散点
hold on;
% Nelder-Mead 求方差最小值点
f = @(x) norm( x(1)*sin(x0 + x(2)) + x(3) - y0 )^2;
c = NelderMead(f, [5, 1, 5], 1e-7);
% 画拟合结果
x = linspace(0, 2*pi, 50);
y1 = c(1) * sin(x + c(2)) + c(3);
plot(x, y1);
% 解线性方程组求方差最小值点
c = sinfit(x0, y0);
% 画拟合结果
y2 = c(1)*cos(x) + c(2)*sin(x) + c(3);
plot(x, y2, '.');
end
% 拟合简谐曲线
% y = C(1)*cos(x) + C(2)*sin(x) + C(3)
function C = sinfit(x, y)
N = numel(x);
cosx = cos(x); sinx = sin(x);
sc = sum(sinx.*cosx);
s = sum(sinx); c = sum(cosx);
% 系数矩阵
M = [sum(cosx.^2), sc , c;
sc, sum(sinx.^2), s;
c, s, N];
b = [sum(y.*cosx); sum(y.*sinx); sum(y)];
C = M\b; % 解线性方程组
end
运行结果如图 1 所示,可见两种方法拟合出的曲线一致(红色的曲线和黄色的点线)。注意第 13 行使用了 “Nelder-Mead 算法” 中的函数 NelderMead 求函数句柄 f 的最小值。
一般参数函数的最小二乘法拟合代码为
代码 2:curveFit.m
% 最小二乘法拟合一元实函数,(x0,y0) 是数据点
% fun 是函数句柄, 格式 y = fun(x, p), 需要支持矢量 x 输入
% p0 是函数初始参数, double 矢量
% 输出最优的 p 以及(局部)最小方差 s
% 使方差 sum(abs(fun(x0, p) - y0).^2) 最小
% p_err 是 NelderMead 算法中 p 的绝对误差
% 返回方均差 err2
function [p, err2] = curveFit(x0, y0, fun, p0, p_err)
% Nelder-Mead 求方差最小值点
f = @(p) sum((fun(x0, p) - y0).^2);
[p, sum_s2] = NelderMead(f, p0, p_err);
err2 = sum_s2 / numel(x0);
end
1. 例子:拟合高斯函数
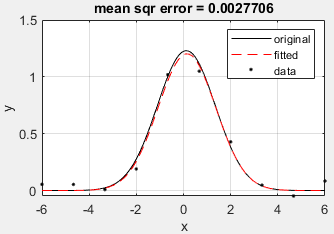
图 2:高斯函数 $A \exp\left[-(x-x_m)^2/(2\sigma^2)\right] $ 的拟合(
fit_gaussian_test.m)
代码 3:fit_gaussian.m
% fit a gaussian distribution
% return mean square error
function [A, xmid, sigma, s2] = fit_gaussian(x0, y0, p_err)
fun = @(x, p) p(1) * exp(-(x-p(2)).^2 / (2*p(3)^2));
[A, ind] = max(y0);
xmid = x0(ind);
sigma = abs(x0(end)-x0(1));
p0 = [A, xmid, sigma];
[p, s2] = curveFit(x0, y0, fun, p0, p_err);
A = p(1); xmid = p(2); sigma = p(3);
end
代码 4:fit_gaussian_test.m
% === params ===
N = 10;
A = 1.23; xmid = 0.12; sigma = 1.23;
% ==============
x = linspace(x0(1), x0(end), 500);
x0 = linspace(-6, 6, N);
y0 = A*exp(-(x0-xmid).^2/(2*sigma^2));
y0_with_err = y0 + 0.2*(rand(1, N)-0.5);
[A_fit, xmid_fit, sigma_fit, s2] = fit_gaussian(x0, y0_with_err, 1e-10);
figure;
plot(x, A*exp(-(x-xmid).^2/(2*sigma^2)), 'k');
hold on;
plot(x, A_fit*exp(-(x-xmid_fit).^2/(2*sigma_fit^2)), 'r--');
plot(x0, y0_with_err, 'k.');
grid on;
xlabel x; ylabel y;
title("mean sqr error = " + mean(s2));
legend({'original', 'fitted', 'data'});