混淆矩阵
贡献者: xzllxls
在机器学习中,混淆矩阵(Confusion Matrix)是一种通过表格可视化的方式呈现分类模型性能的常用工具,能够显示出模型预测值与实际标签之间的对应关系。顾名思义,混淆矩阵能够方便地看出模型是否将两个不同的类混淆了(比如把一个类错误地判定为另一类)以及混淆的数量有多少。
要弄清楚混淆矩阵,首先必须了解以下基本概念。
- True Positive(TP):真正类。样本的真实类别是正类,并且模型也将其判定为正类。
- False Negative(FN):假负类。样本的真实类别是正类,但模型将其判定为负类。
- False Positive(FP):假正类。样本的真实类别是负类,但模型将其判定为正类。
- True Negative(TN):真负类。样本的真实类别是负类,并且模型将其判定为负类。
对于二分类问题而言,混淆矩阵包含两行、两列,一共四个单元格。列(行)分别表示分类器预测的值,行(列)分别表示实际的值。如表 1 所示。
| 预测为正类 (Positive) | 预测为负类 (Negative) | |
| 实际为正类(Positive) | 真正类 (TP) | 假负类 (FN) |
| 实际为负类(Negative) | 假正类 (FP) | 真负类 (TN) |
举个例子,现在有一个训练好的二元分类器,用于判断给定图片上的动物是马还是羊。假设,有一个图片数据集,一共 14 张图片,其中 9 只为羊,5 只为马。假设用 0 表示羊,1 表示马。样本情况可以表示为表 2 。
| 样本编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 实际类别 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
现在用训练好的分类器来做判断,有可能产生下面的结果。
| 样本编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 实际类别 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 预测类别 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
从表 3 中可以看出,实际有 9 只羊,模型预测正确了 6 只(预测为羊),预测错了 3 只(预测为马)。马实际上有 5 匹,模型预测正确了 4 只(预测为马),预测错了 1 匹(预测为羊)。把结论写下来,就形成了如表 4 所示的混淆矩阵。
| 预测为马 | 预测为羊 | |
| 实际为马 | 4 | 1 |
| 实际为羊 | 3 | 6 |
设样本总数用 N 表示,本例中 N=14。显然,当只给定混淆矩阵时,也可以从中算出样本总数:N=TP+FN+FP+TN=14。由混淆矩阵,我们可以得出对于模型的多个常规的评价指标。
精确率(Accuracy),或者称精度:最常用的分类性能指标。可以用来表示模型的分类精度,即模型识别正确的个数/样本的总个数。
本例模型精度 = (TP+TN)/N=(4+6)/14=10/14
准确率(Precision),又称查准率:表示在模型判定为正类的样本中,真正为正类的样本所占的比例。
本例准确率 = TP/(TP+FP)=4/(4+3)=4/7
召回率(Recall),又称查全率:在实际正样本中,模型判定正确的数量。
本例召回率=TP/(TP+FN)=4/(4+1)=4/5
特异度(Specificity):实际为负类的样本中被模型正确判定为负类的比例。
本例特异度=TN/(TN+FP)=6/(6+3)=2/3
F1 分数(F1 score):准确率和召回率的调和平均数。
本例 F1 分数 = $ 2 \times \frac{Precision \times Recall}{Precision + Recall} = 2 \times \frac{(4/7) \times (4/5)}{4/7+4/5}$
1. 程序实战
给出一段求混淆矩阵和各个量化评价指标的示例程序。该程序基于 scikit-learn 机器学习库,数据表示基于 numpy 库。
代码示例
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix,
accuracy_score, precision_score, recall_score, f1_score
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
# 加载数据集
data = load_iris()
X = data.data
y = data.target
# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split
(X, y, test_size=0.2, random_state=42)
# 定义和训练模型
model = LogisticRegression(max_iter=200)
model.fit(X_train, y_train)
# 在测试集上预测
y_pred = model.predict(X_test)
# 计算混淆矩阵
cm = confusion_matrix(y_test, y_pred)
# 打印混淆矩阵
print("混淆矩阵:")
print(cm)
# 可视化混淆矩阵
plt.figure(figsize=(10,7))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
xticklabels=data.target_names, yticklabels=data.target_names)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()
# 计算其他评价指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
f1 = f1_score(y_test, y_pred, average='weighted')
# 打印评价指标
print(f"准确率:{accuracy}")
print(f"精确率:{precision}")
print(f"召回率:{recall}")
print(f"F1得分:{f1}")
结果与说明
程序首先下载读取公开的 iris 数据集,然后训练一个逻辑回归模型来做分类。训练方法采用留出法。模型训练完成之后,计算混淆矩阵,并计算几个常用的评价指标。
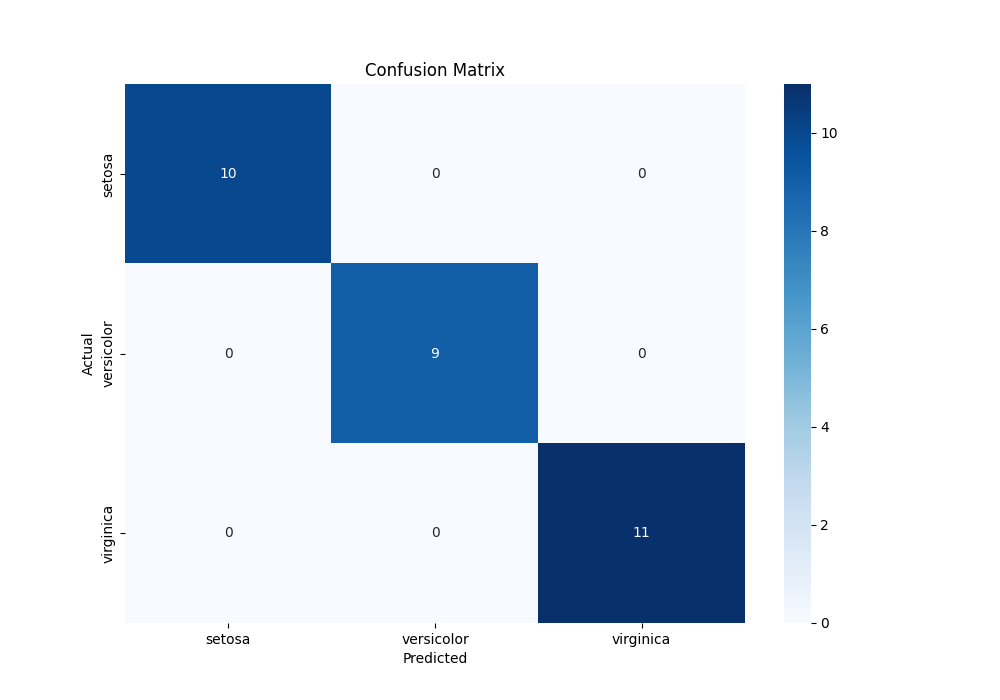
由于数据集有三个类别标签,因此本例是一个三分类问题。混淆矩阵是一个 $3 \times 3$ 方阵,如图 1 所示:
量化评价指标结果如下:
准确率:1.0
精确率:1.0
召回率:1.0
F1得分:1.0