贡献者: addis; FFjet; _Eden_; int256
1. 卡诺热机的工作过程
卡诺循环(Carnot cycle)是一个特别的热力学循环,使用在一个假想的卡诺热机上,由法国人尼古拉·卡诺于 1824 年提出,埃米尔·克拉佩龙于 1830 年代至 1840 年代扩充,是为了找出热机的最大的工作效率而分析热机的工作过程。
图 1:热机示意图(来自维基百科)
卡诺循环由两个等温过程,两个绝热过程,下面先通过两个图来直观感受一下卡诺热机的工作过程。
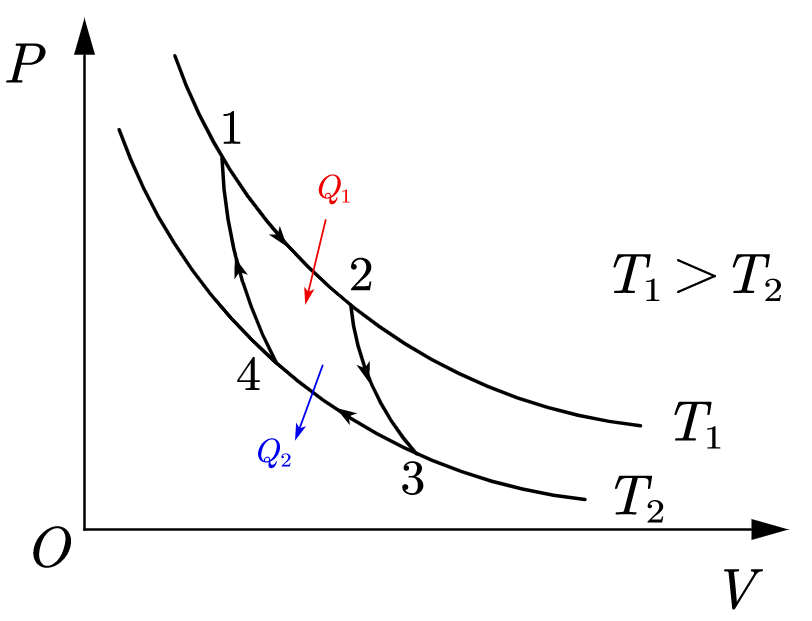
压强-体积图,即 $P$-$V$ 图,是大家十分熟悉的:
图 2:卡诺循环的压强-体积图
温度-熵图(见熵的宏观定义),即 $T$-$S$ 图,则如下所示:
图 3:卡诺循环的温度-熵图
图 2 $1\to 2$、图 3 $A\to B$,可逆等温膨胀:此等温的过程中系统从高温热库吸收了热量且全部拿去做功。
图 2 $2\to 3$、图 3 $B\to C$,等熵(可逆绝热)膨胀:移开热库,系统对环境做功,其能量来自于本身的内能。
图 2 $3\to 4$、图 3 $C\to D$,可逆等温压缩:此等温的过程中系统向低温热库放出了热量。同时环境对系统做正功。
图 2 $4\to 1$、图 3 $D\to A$,等熵(可逆绝热)压缩:移开低温热库,此绝热的过程系统对环境作负功,系统在此过程后回到原来的状态。
2. 卡诺循环的效率(理想气体)
下面我们来分析一下理想气体卡诺循环的效率。气体在等温膨胀过程中,从高温热源吸取热量,根据等温过程吸热公式(式 3 ),我们有
\begin{equation}
Q_{1}=\frac{m}{M} R T_{1} \ln \frac{V_{2}}{V_{1}}~,
\end{equation}
气休在等温压缩过程中向低温热源放出热量 $Q_2$,为便于研究,取绝对值,有
\begin{equation}
Q_{2}=\frac{m}{M} R T_{2} \ln \frac{V_{3}}{V_{4}}~.
\end{equation}
应用绝热过程方程(
式 3 )$T_{1} V_{2}^{\gamma-1}=T_{2} V_{3}^{\gamma-1}$ 和 $T_{1} V_{1}^{\gamma-1}=T_{2} V_{4}^{\gamma-1}$ 可得
\begin{equation}
\left(\frac{V_{2}}{V_{1}}\right)^{\gamma-1}=\left(\frac{V_{3}}{V_{4}}\right)^{\gamma-1}~.
\end{equation}
也就是说
\begin{equation}
\frac{V_{2}}{V_{1}}=\frac{V_{3}}{V_{4}}~,
\end{equation}
所以有
\begin{equation}
Q_{2}=\frac{m}{M} R T_{2} \ln \frac{V_{3}}{V_{4}}=\frac{m}{M} R T_{2} \ln \frac{V_{2}}{V_{1}}~.
\end{equation}
取 $Q_1$ 与 $Q_2$ 的比值,可得
\begin{equation}
\frac{Q_{1}}{T_{1}}=\frac{Q_{2}}{T_{2}}~,
\end{equation}
因此卡诺热机的效率为
\begin{equation}
\eta_{\mathrm{c}}=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{2}}{T_{1}}~.
\end{equation}
卡诺热机有几条重要性质,我们做个总结:
- 要完成一次卡诺循环必须有高温和低温两个热源;
- 卡诺循环的效率只与两个热源的温度有关,高温热源的温度越高,低温热源的温度越低,卡诺循环的效率越大,也就是说节两热源的温度差越大,从高温热源所吸取的热量 $Q_1$ 的 “利用价值” 越大;
- 卡诺循环的效率总足小于 $1 $ 的。
实际上,卡诺循环还有个逆循环过程,功能应该都可以猜到,也就是制冷机。通过类似对卡诺循环的分析,可以得到制冷系数
\begin{equation}
w_{\mathrm{C}}=\frac{Q_{2}}{A}=\frac{Q_{2}}{Q_{1}-Q_{2}}=\frac{T_{2}}{T_{1}-T_{2}}~.
\end{equation}
例 1 卡诺制冷机
有一卡诺制冷机,从温度为 $-10^{\circ} \mathrm{C}$ 的冷藏室吸取热量,而向温度为 $20^{\circ} \mathrm{C}$ 的物体放出热量。设该制冷机所耗功率为 $15\rm kW$, 问每分钟从冷藏室吸取的热量为多少?
令 $T_1 = 293 \mathrm K , T_2 = 263 \mathrm K $,则
\begin{equation}
w=\frac{T_{2}}{T_{1}-T_{2}}=\frac{263}{30}~.
\end{equation}
每分钟做功为
\begin{equation}
A=15 \times 10^{3} \times 60 \mathrm{J}=9 \times 10^{5} \mathrm{J}~,
\end{equation}
所以每分钟从冷藏室中吸取的热量为
\begin{equation}
Q_{2}=w A=7.89 \times 10^{6} \mathrm{J}~.
\end{equation}
此时,每分钟向温度为 $20^{\circ} \mathrm{C}$ 的物体放出的热量为
\begin{equation}
Q_{1}=Q_{2}+A=8.79 \times 10^{6} \mathrm{J}~.
\end{equation}
3. 可逆卡诺循环
对于可逆卡诺循环,可以证明一个循环后熵不改变(克劳修斯不等式取等号)
\begin{equation}
\Delta S = \oint \frac{\delta Q}{T}=0~.
\end{equation}
这不止对于理想气体,对于任意的热力学系统都是成立的。
首先,由卡诺定理(证明见热力学第二定律 子节 2 ),对于工作于温度固定的两热源间的卡诺热机,其效率总为
$$\eta = 1- \frac{Q_2}{Q_1} = 1-\frac{T_2}{T_1}~.$$
于是就有
$$\frac{Q_2}{Q_1} = \frac{T_2}{T_1} ~,$$
从而,
$$\frac{Q_2}{T_2} = \frac{Q_1}{T_1} ~.$$
现约定 $Q$ 代表吸收的热量,则放出的热量为 $-Q$,故上式可写为
\begin{equation}
\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0~.
\end{equation}
推广到 $n$ 个热源的情况即为
\begin{equation}
\sum_{i=1}^{n} \frac{Q_i}{T_i} = 0 ~.
\end{equation}
对于连续情况,求极限即可证明原积分等式 $\oint \frac{\delta Q}{T} = 0$。
由于是可逆循环,$Q_{rev} = Q$,故 $ \,\mathrm{d}{S} = \frac{\delta Q_{rev}}{T} = \frac{\delta Q}{T}$。故
\begin{equation}
\Delta S = \int \,\mathrm{d}{S} = \int {\frac{\delta Q}{T}} = \oint {\frac {\delta Q}{T}} = 0~.
\end{equation}
得证。