相机模型
贡献者: addis
- 本文处于草稿阶段。
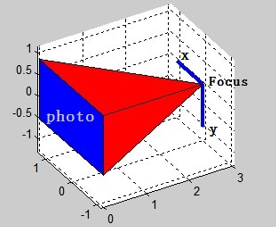
图 1:相机坐标系
从焦点出发,穿过底片并与底片垂直的射线叫做光轴。
以焦点为原点,光轴方向为 $z$ 轴,图片的右方为 $x$ 轴,下方为 $y$ 轴(注意这是常用的右手系)。
真实的相机和这里的相机模型存在误差,通常需要将图片进行纠偏后才能得到符合模型的图像。以后我们讨论的图像一般指纠偏后的图像。
注意图像的中点不一定是光轴和底片的交点。
相机参数:焦距,底片宽度,底片高度,光轴的图像坐标
相机的位置参数:焦点的位置,三个单位矢量在世界坐标系中的坐标(即旋转矩阵,也可以使用四元数表示)
反过来,若已知图片和相机位置和参数,我们可以将图片上的每一点对应到以相机为起点的一条射线。而至于这点具体在射线上的什么位置无从得知。但如果我们从两个不同的位置拍摄同一点,就可以通过两条射线的交点确定该点位置。
若已知相机参数,我们可以通过图片中的任意两点确定它们关于相机的夹角(即两条射线的夹角)。
1. 变换方程
变换有 7 个自由度,相机位置 3 个,相机角度 3 个,相机焦距 1 个。
一般形式为(推导:根据相机模型结合立体几何)
\begin{equation}
\left\{\begin{aligned}
x' &= \frac{c_4 x + c_5 y + c_6 z + c_7}{c_1 x + c_2 y + c_3}\\
y' &= \frac{c_8 x + c_9 y + c_{10} z + c_{11}}{c_1 x + c_2 y + c_3}
\end{aligned}\right. ~
\end{equation}
如果我们不仅需要得到变换公式,还需要从这些系数里面得到相机的位置和朝向,那么我们可以从立体几何的角度出发,例如见长方形相机定位法。但这样我们需要的 4 个点就必须是长方形的四个顶点而不是任意点。
2. 平面到平面的变换
注意式 1 不存在逆变换,因为我们把空间中的点投影到平面上时丢失了景深的信息。但如果我们限制所有空间点 $(x, y, z)$ 都在某个平面上(不失一般性,假设它们在 $x$-$y$ 平面上),那两个平面上的点就有一一对应的关系。
\begin{equation}
\left\{\begin{aligned}
x' &= \frac{c_4 x + c_5 y + c_6}{c_1 x + c_2 y + c_3}\\
y' &= \frac{c_7 x + c_8 y + c_9}{c_1 x + c_2 y + c_3}
\end{aligned}\right. ~
\end{equation}