BCS-BEC Crossover 的平均场描述
贡献者： addis
仍然沿用 BCS 的 Hamiltonian，在动量空间里面，
\begin{equation}
H-\mu N = \sum_{{ \boldsymbol{\mathbf{k}} },\sigma}(\epsilon_{ \boldsymbol{\mathbf{k}} }-\mu)a ^\dagger _{{ \boldsymbol{\mathbf{k}} },\sigma}a_{ \boldsymbol{\mathbf{k}} , \boldsymbol{\mathbf{\sigma}} }+\frac{1}{V}\sum_{ \boldsymbol{\mathbf{k}} , \boldsymbol{\mathbf{k}} '}U_{ \boldsymbol{\mathbf{k}} , \boldsymbol{\mathbf{k}} '}a ^\dagger _{ \boldsymbol{\mathbf{k}} \uparrow}a ^\dagger _{- \boldsymbol{\mathbf{k}} \downarrow}a_{- \boldsymbol{\mathbf{k}} \downarrow}a_{ \boldsymbol{\mathbf{k}} \uparrow}~.
\end{equation}
假设不是一个微扰的情况下，也可以用 $|\Psi\rangle = \prod_{ \boldsymbol{\mathbf{k}} }(u_{ \boldsymbol{\mathbf{k}} }+v_{ \boldsymbol{\mathbf{k}} }a ^\dagger _{ \boldsymbol{\mathbf{k}} \uparrow}a ^\dagger _{- \boldsymbol{\mathbf{k}} \downarrow})|0\rangle$ 来描述基态。仍然定义平均场参数 $\Delta = \langle a_{- \boldsymbol{\mathbf{k}} \downarrow},a_{ \boldsymbol{\mathbf{k}} \uparrow}\rangle$。不同的是，研究冷原子问题的时候，并不是只有在费米面附近才有 $U$，而是一个队任意动量都可以的情况。重复同样的 Bogoliubov 变换，我们能够解出来 $u_{ \boldsymbol{\mathbf{k}} }^2, v_{ \boldsymbol{\mathbf{k}} }^2 = 1/2(1\pm\epsilon_{ \boldsymbol{\mathbf{k}} }/E_{ \boldsymbol{\mathbf{k}} })$，其中元激发的能级关系 $E_{ \boldsymbol{\mathbf{k}} }=\sqrt{(\epsilon_{ \boldsymbol{\mathbf{k}} }-\mu)^2+|\Delta|^2}$。利用自洽方程，我们得到
\begin{equation}
-\frac{1}{U} = \frac{1}{V}\sum_{ \boldsymbol{\mathbf{k}} }\frac{1}{2E_{ \boldsymbol{\mathbf{k}} }}~,
\end{equation}
\begin{equation}
\frac{ma_s}{4\pi\hbar^2} = \frac{1}{g} + \frac{1}{V}\sum_{ \boldsymbol{\mathbf{k}} }\frac{1}{\hbar^2{ \boldsymbol{\mathbf{k}} }^2/m} = \frac{1}{V}\sum_{ \boldsymbol{\mathbf{k}} }\left(\frac{1}{2\epsilon_{ \boldsymbol{\mathbf{k}} }} - \frac{1}{2E_{ \boldsymbol{\mathbf{k}} }}\right)~.
\end{equation}
\begin{equation}
x^2 = \frac{\hbar^2{ \boldsymbol{\mathbf{k}} }^2}{2m}\frac{1}{\Delta},\quad x_0 = \frac{\mu}{\Delta},\quad \epsilon_x = x^2-x_0 = \frac{\epsilon_{ \boldsymbol{\mathbf{k}} }-\mu}{\Delta},\quad E_x = \sqrt{1+\epsilon_x^2} = \frac{E_{ \boldsymbol{\mathbf{k}} }}{\Delta}~
\end{equation}
\begin{equation}
\begin{split}
-\frac{m\Delta}{4\pi\hbar^2 a_s} &=\frac{1}{V}\sum_{ \boldsymbol{\mathbf{k}} }\left(\frac{\Delta}{2E_{ \boldsymbol{\mathbf{k}} }} - \frac{\Delta}{2\epsilon_{ \boldsymbol{\mathbf{k}} }}\right)~,\\
-\frac{m\Delta}{4\pi\hbar^2 a_s} &=\int_0^\infty\frac{\text{d}^3{ \boldsymbol{\mathbf{k}} }}{(2\pi)^3}\left(\frac{1}{2E_x} - \frac{1}{2x^2}\right)~,\\
&=\int_0^\infty\frac{\text{d}k\cdot 4\pi k^2}{(2\pi)^3}\left(\frac{1}{2E_x} - \frac{1}{2x^2}\right)~,\\
-\frac{1}{a_s} &= \frac{2}{\pi\Delta}\frac{\hbar^2}{m}\int_0^\infty\text{d}k\cdot k^2\left(\frac{1}{2E_x} - \frac{1}{2x^2}\right)~,\\
k^2 &= \frac{mx^2}{\hbar^2}~,\\
-\frac{1}{a_s} &= \frac{2}{\pi}\sqrt{\frac{2m\Delta}{\hbar^2}}\int_0^\infty \text{d}x\cdot x^2\left(\frac{1}{E_x}-\frac{1}{x^2}\right)~.
\end{split}
\end{equation}
\begin{equation}
I_1(x_0) = \int_0^\infty \text{d}x\cdot x^2\left(\frac{1}{E_x}-\frac{1}{x^2}\right)~.
\end{equation}
\begin{equation}
N = \sum_{ \boldsymbol{\mathbf{k}} }\left(1-\frac{\epsilon_{ \boldsymbol{\mathbf{k}} }-\mu}{E_{ \boldsymbol{\mathbf{k}} }}\right)~.
\end{equation}
\begin{equation}
\begin{split}
n &= \frac{1}{V}\sum_{ \boldsymbol{\mathbf{k}} }\left(1-\frac{\epsilon_{ \boldsymbol{\mathbf{k}} }-\mu}{E_{ \boldsymbol{\mathbf{k}} }}\right)\\
&=\frac{1}{V}\sum_{ \boldsymbol{\mathbf{k}} }\left(1-\frac{\epsilon_x{\Delta}}{E_x{\Delta}}\right)\\ &=\int_0^\infty\frac{\text{d}k \cdot 4\pi k^2}{(2\pi)^3}\left(1-\frac{\epsilon_x}{E_x}\right)\\
&=\frac{1}{2\pi^2}\frac{2m\Delta}{\hbar^2}\sqrt{\frac{2m\Delta}{\hbar^2}}\int_0^\infty\text{d}x\cdot x^2\left(1-\frac{\epsilon_x}{E_x}\right)\\
&=\frac{1}{2\pi^2}\left(\frac{2m\Delta}{\hbar^2}\right)^{3/2}I_2(x_0)~,
\end{split}
\end{equation}
\begin{equation}
I_2(x_0)=\int_0^\infty \text{d}x\cdot x^2\left(1-\frac{\epsilon_x}{E_x}\right)~.
\end{equation}
\begin{equation}
\begin{cases}
\dfrac{\Delta}{E_F} = \left(\dfrac{2}{3I_2(x_0)}\right)^{2/3}\\
\ \\
\dfrac{1}{k_Fa_s} = -\dfrac{2}{\pi}\left(\dfrac{2}{3I_2(x_0)}\right)^{1/3}I_1(x_0)
\end{cases}
~.
\end{equation}
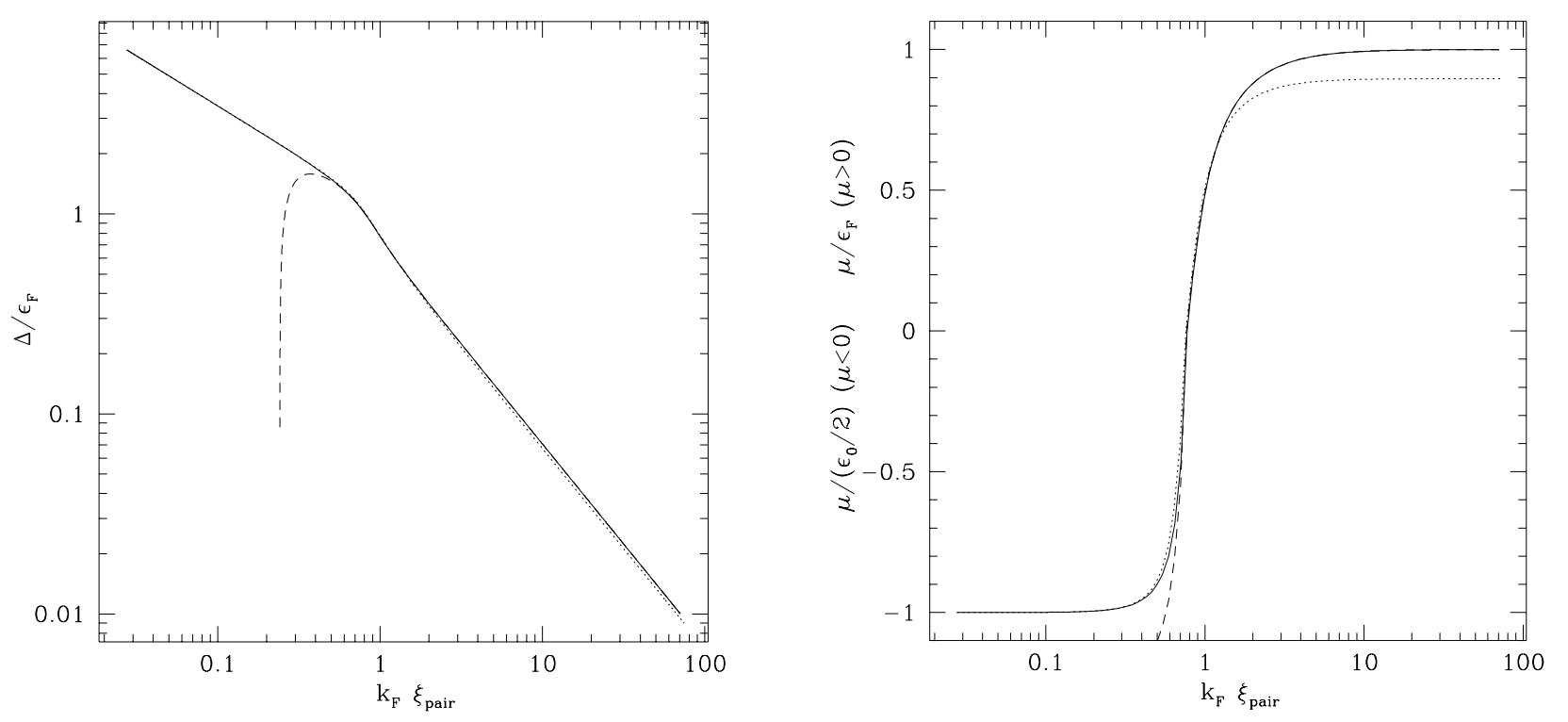
图 1：左：$\Delta/E_F$ vs $k_F\xi_{\text{pair}}$，右：$\mu/E_F(\mu>0), \mu/(\epsilon_0/2)(\mu<0)$，区分两种情况是因为在 Bose 情况下没有费米能的定义，$\epsilon_0\equiv1/(ma_s^2)$
但是，对于 $I_1, I_2$ 的渐进行为并不好分析，我们定义更多的积分
\begin{equation}
\begin{aligned}
I_3(x_0) &=\int_0^\infty\text{d}x\frac{x^4\epsilon_x}{E_x^6}~,\\
I_4(x_0) &=\int_0^\infty\text{d}x\frac{x^2}{E_x^2}~,\\
I_5(x_0) &=\int_0^\infty\text{d}x\frac{x^2}{E_x^3}~,\\
I_6(x_0) &=\int_0^\infty\text{d}x\frac{x^2\epsilon_x}{E_x^3}~.
\end{aligned}
\end{equation}
可以知道，$I_1=(2x_0I_6-I_5),I_2 = \frac{2}{3}(x_0I_5+I_6)$。而 $I_3,I_4$ 是很好计算的。如果定义
\begin{equation}
x_1^2=\frac{x_0+\sqrt{1+x_0^2}}{2}~,
\end{equation}
\begin{equation}
\begin{aligned}
I_3&=\frac{\pi}{16}\frac{x_1(1+x_1^4)}{(1+x_0^2)^{1/2}}~,\\
I_4&=\frac{\pi}{2}x_1~.
\end{aligned}
\end{equation}
平均场下可以计算费米子对的特征距离
\begin{equation}
\xi_{\text{pair}}^2 = \frac{1}{m^2}\frac{\int_0^\infty\text{d}k(k^4(\epsilon_{ \boldsymbol{\mathbf{k}} }-\mu)^2/E_{ \boldsymbol{\mathbf{k}} }^6)}{\int_0^\infty\text{d}k(k^2/E_{ \boldsymbol{\mathbf{k}} }^2)} = \frac{2}{m\Delta}\frac{I_3}{I_4}~,
\end{equation}
\begin{equation}
\begin{aligned}
\frac{\Delta}{E_F} &= \left(\frac{1}{x_0I_5+I_6}\right)^{2/3}~,\\
\frac{\mu}{E_F} &= x_0\frac{\Delta}{E_F}~,\\
\frac{1}{k_Fa_s} &= -\frac{4}{\pi}\frac{x_0I_6-I_5}{(x_0I_5+I_6)^{1/3}}~,\\
k_F\xi_{\text{pair}} &= \sqrt{\frac{1+x_1^4}{2}}\frac{(x_0I_5+I_6)^{1/3}}{(1+x_0^2)^{1/4}}~.
\end{aligned}
\end{equation}
现在仔细分析一下渐进行为：
- $x_0\to\infty$，此时 $\mu\to E_F$，$I_5\sim\sqrt{x_0}$，$I_6\sim\ln x_0/(2\sqrt{x_0})$，我们的 $1/k_Fa_s\to(2/\pi)\ln x_0$，$a_s\to0^+$，表现为微弱的吸引力，就是 BCS 态的情况。此时 $k_F\xi_{\text{pair}}\to x_0/\sqrt2$。
- $x_0\to-\infty$，$I_5\sim\pi/(16|x_0|^{3/2}), I_6\sim\pi/(4|x_0|^{1/2})$。此时 $\Delta\to\infty, \mu\to-\infty, a_s\to0^+,k_F\xi_{\text{pair}}\to0^+$。表现为强吸引力（$\Delta$），就是 BEC 极限。
可以用 $k_f\xi_{\text{pair}}$ 作为参数反解很多信息，如图 1 。