充分必要条件
贡献者: 叶燊Leafshen; addis
未完成:另开文章
1. 韦恩图
韦恩图(Veen diagram),是在所谓的集合论(或者类的理论)数学分支中,在不太严格的意义下用以表示集合(或类)的一种草图。它们用于展示在不同的事物群组(集合)之间的数学或逻辑联系,尤其适合用来表示集合(或)类之间的 “大致关系”。它也常常被用来帮助推导(或理解推导过程)关于集合运算(或类运算)的一些规律。
图 1:Veen 图
条件越多,在韦恩图上范围就越小,这似乎很好理解。
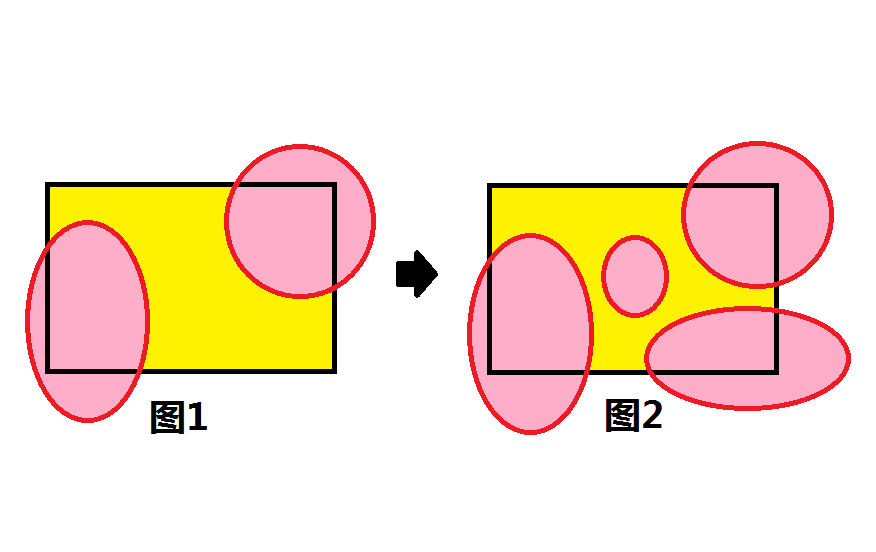
我们将全集用黄色来表示,一个个限制条件瓦解侵蚀,我们用粉色来标记。那么,如图所示:
图 2:条件越多,在韦恩图上范围就越小
2. 学科联系
在语文逻辑中,我们这样解释: “马” 是一类事物的总称。限制条件诸如 “高大的”“白色的”“会飞的” 等等,具体了其内涵,缩小了其外延。
概念的内涵就是指反映在概念中的对象的本质属性或特有属性。
概念的外延是指具有概念所反映的本质属性或特有属性的对象,即概念的适用范围。
两者的区别:
1. 本质不同: 内涵是 “属性”,外延是 “范围”。属性越多,则符合这个属性的范围越小。属性越少,符合这个属性的范围就越大。
2. 侧重不同: 概念的内涵是指概念的质的方面。 概念的外延是指概念的量的方面。
若由命题 $A$ 能推导出命题 $B$,则 $A$ 是 $B$ 的充分条件,$B$ 是 $A$ 的必要条件。如何理解这个定义呢?下面举两个例子。
需要注意的是:
- 充分/必要条件是两个命题之间的关系,若直说一个命题是充分/必要条件没有意义。
- 讨论充分/必要条件需要在一定的前提下进行。以上两个例子中的前提如:我们讨论的是欧几里得几何中的平面四边形和三角形。当然,我们也可以把这个前提直接写在每个命题中。
- 在证明 $A$ 是 $B$ 的充分必要条件时,需要分别证明 $A$(相对于 $B$)的充分性和必要性。充分性需要由 $A$ 证明 $B$,必要性需要由 $B$ 证明 $A$。
- 在证明 $A$ 是 $B$ 的充分非必要条件时,除了需要证明 $A$ 的充分性,还需非必要性,即 $B$ 不能推出 $A$。只要我们可以举出一个 $B$ 成立 $A$ 不成立的反例,就立刻证明了不可能由 $B$ 推出 $A$。
简要说明:
有命题 $A$ 和 $B$
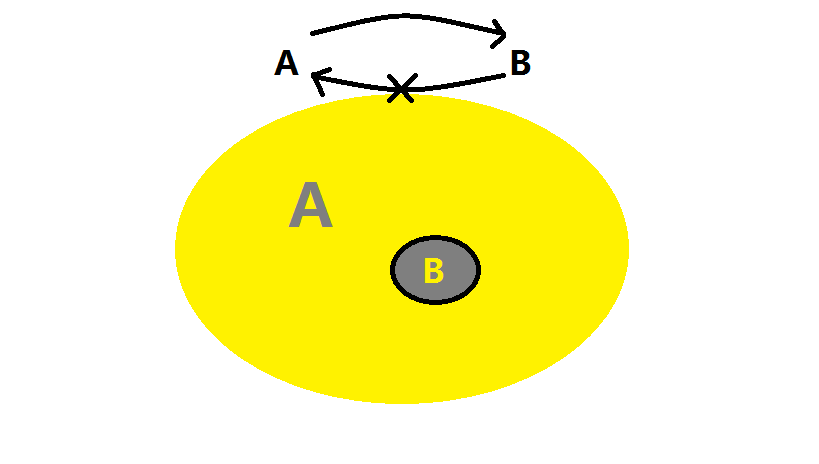
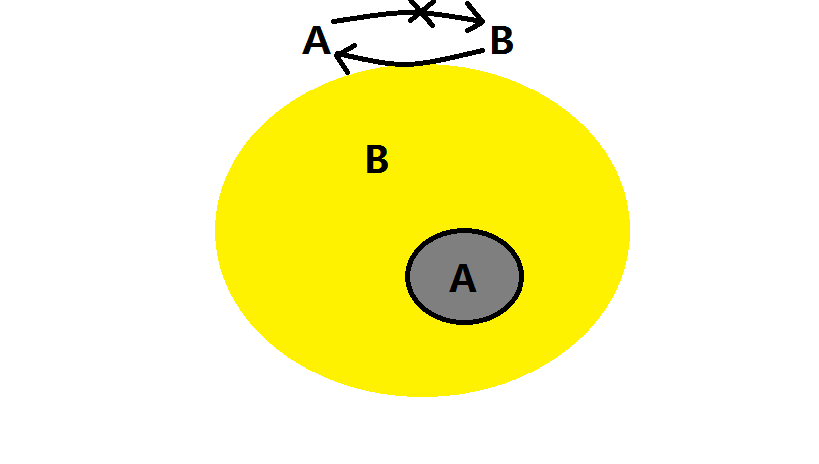
- $A$ 推出 $B$,$B$ 推不出 $A$,则为充分不必要,如图:
图 3:充分不必要口诀:有之必然,无之未必不然
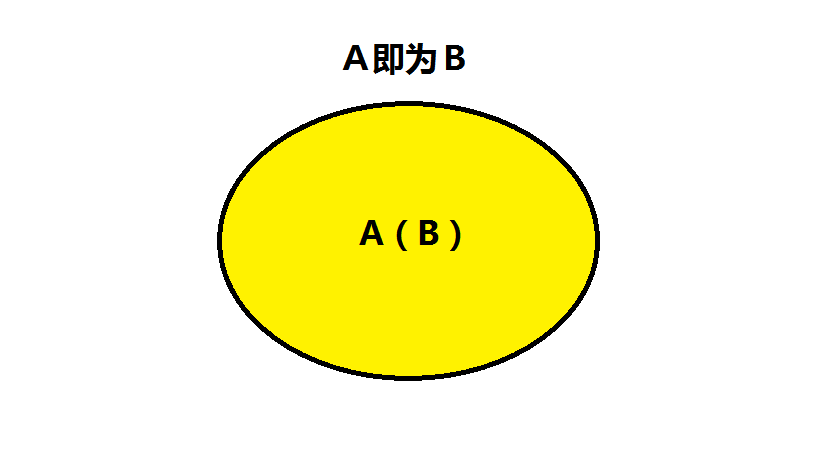
- $A$ 推出 $B$,$B$ 推出 $A$,则为充要,如图:
图 4:充要
- $A$ 推不出 $B$,$B$ 推不出 $A$,则既不充分也不必要,如图:
图 5:既不充分也不必要
- $A$ 推不出 $B$,$B$ 推出 $A$,则必要不充分,如图:
图 6:必要不充分口诀:有之未必然,无之必不然
致读者: 小时百科一直以来坚持所有内容免费,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 10 元,我们一个星期内就能脱离亏损, 并保证在接下来的一整年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。
友情链接: 超理论坛 | ©小时科技 保留一切权利