詹姆斯·格雷果里（James Gregory）（综述）

贡献者：待更新

　　本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

图 1：约翰·斯库加尔绘《格雷戈里》，约 1675 年

　　詹姆斯·格雷戈里（James Gregory FRS，1638 年 11 月－1675 年 10 月）是一位苏格兰数学家和天文学家。他的姓氏有时拼作 Gregorie，这是苏格兰的原始拼法。他提出了反射望远镜的早期实用设计——格里高利望远镜，并在三角学方面取得进展，发现了若干三角函数的无穷级数展开。

　　在他的著作《几何学的普遍部分》（Geometriae Pars Universalis，1668 年）$^\text{[1]}$ 中，格雷戈里首次发表并证明了微积分基本定理（从几何角度陈述，并且仅限于后来版本定理所考虑曲线的一类特殊情况）。艾萨克·巴罗对此予以承认。$^\text{[2][3][4][5][6][7]}$

1. 生平

　　格雷戈里出生于 1638 年。他的母亲珍妮特是琼和大卫·安德森的女儿，父亲约翰·格雷戈里是一位苏格兰圣公会牧师。詹姆斯是他们三个孩子中最小的一个，出生在阿伯丁郡德鲁莫克的牧师住宅中，最初由母亲珍妮特·安德森（约 1600–1668）在家中教育。正是他的母亲激发了他对几何学的兴趣，因为她的叔叔——亚历山大·安德森（Alexander Anderson, 1582–1619）曾是法国数学家维达的学生和著作编辑。在 1651 年父亲去世后，他的哥哥大卫接管了对他的教育。他先后就读于阿伯丁文法学校和马里斯哈尔学院（1653–1657），并于 1657 年获得艺术硕士学位（AM）。

　　 1663 年，他前往伦敦，结识了约翰·柯林斯以及苏格兰同胞罗伯特·穆雷（Robert Moray，皇家学会创始人之一）。1664 年，他前往威尼斯共和国的帕多瓦大学，在途中途经佛兰德、巴黎和罗马。在帕多瓦，他与同乡、哲学教授詹姆斯·卡登黑德同住，并师从斯特凡诺·安杰利。他在帕多瓦发表的几何学论文《真正的圆和双曲线求积》（Vera circuli et hyperbolæ quadratura, 1667）和《几何学的普遍部分》（Geometriæ pars universalis, 1668），见证了安杰利及其他意大利著名数学家（如加布里埃莱·曼弗雷迪）对他的深刻影响 $^\text{[9]}$。

　　 1668 年返回伦敦后，他当选为皇家学会院士。同年晚些时候，他前往圣安德鲁斯大学，担任首任皇家数学教授，该职位由查理二世设立，很可能是应罗伯特·穆雷的请求。在圣安德鲁斯大学，他于 1673 年在实验室地板上铺设了第一条子午线，比格林尼治子午线确立早了 200 年，因此被认为 “可以说圣安德鲁斯是时间的起点”$^\text{[10][11]}$。

　　他先后在圣安德鲁斯大学和爱丁堡大学任教。

　　他与乔治·詹姆森（George Jameson，画家）的女儿、约翰·伯内特（John Burnet，来自阿伯丁埃尔里克）的遗孀玛丽结婚；他们的儿子詹姆斯成为阿伯丁国王学院的物理学教授。他是约翰·格雷戈里（John Gregory，1756 年当选皇家学会院士）的祖父，大卫·格雷戈里（David Gregorie，1692 年当选皇家学会院士）的叔叔，以及医生和发明家大卫·格雷戈里（1627–1720）的弟弟。

　　在担任爱丁堡大学数学讲座教授约一年后，詹姆斯·格雷戈里在与学生观测木星卫星时突发中风，几天后去世，享年 36 岁。

2. 出版著作

《光学的推广》

图 2：《圆与双曲线的求积》，1667 年

　　在 1663 年出版的 Optica Promota（《光学的推广》）中，格雷戈里描述了他设计的一种反射望远镜，即 “格里高利望远镜”。他还提出了一种通过金星凌日测量地球到太阳距离的方法，这一方法后来被埃德蒙·哈雷提倡，并最终被采纳为首次有效测定天文单位的基础。

《圆与双曲线的求积》

　　在离开帕多瓦之前，格雷戈里出版了 Vera Circuli et Hyperbolae Quadratura（1667，《圆与双曲线的求积》），在其中他用收敛级数逼近圆与双曲线的面积：

　　 [詹姆斯·格雷戈里] 无疑是许多关于圆与内接、外切多边形之间关系以及它们相互关系的奇妙定理的作者。借助这些定理，他比通过通常的计算要轻松得多地给出了圆与双曲线（因此也包括对数的构造）的测度，精确到二十多位小数。继惠更斯之后，他还给出了与圆弧相等的直线构造方法，并且误差更小。$^\text{[12]}$

　　 “微积分基本定理的首次证明和泰勒级数的发现都可归功于他。”$^\text{[13][14]}$

　　此书在 1668 年再版，并附有一篇附录 Geometriae Pars（《几何部分》），在其中格雷戈里解释了如何求解旋转体的体积。

3. 格里高利望远镜

图 3：格里高利反射望远镜示意图

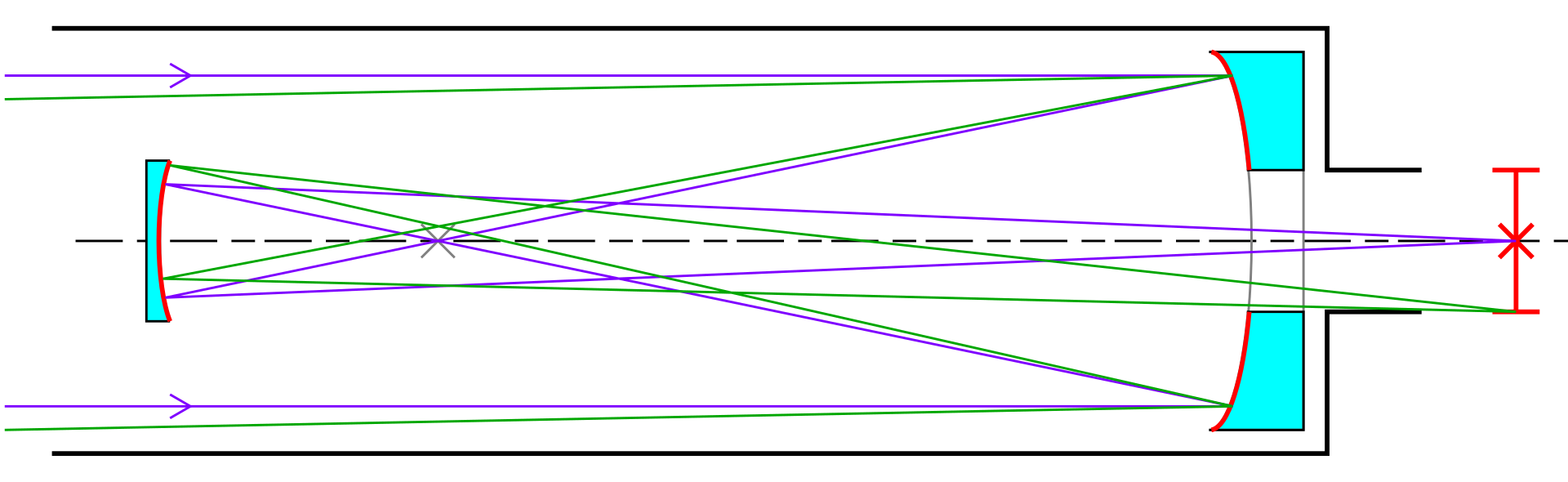
　　在他 1663 年的著作《Optica Promota》中，詹姆斯·格里高利描述了一种反射望远镜，这种设计后来以他的名字命名为 “格里高利望远镜”。格里高利指出，使用抛物面镜的反射望远镜不仅能校正球面像差，还能修正折射望远镜中出现的色差。在他的设计中，他还在抛物面主镜焦点之后安置了一面椭圆曲面的凹面副镜，把成像反射回主镜中央的孔洞，从而使观测者能够方便地观察图像。按照他本人的坦言，他缺乏实际操作技能，而且当时也找不到能够真正制作这种望远镜的光学工匠。$^\text{[15]}$

　　这种望远镜的设计吸引了科学界一些人士的关注，例如牛津物理学家罗伯特·胡克，他最终在十年后建造了这种望远镜；以及博学多才并且是英国皇家学会创始成员的罗伯特·穆雷爵士。

　　如今，格里高利望远镜的设计已很少被采用，因为其他类型的反射望远镜在常规应用中效率更高。不过，格里高利光学仍被用于一些射电望远镜，例如阿雷西博天文台，其设计中就有一个 “格里高利穹顶”。$^\text{[16]}$

4. 数学

　　以下摘自《Pantologia. A new (cabinet) cyclopædia》（1813）：

　　詹姆斯·格里高利先生是一位才智极为敏锐而深刻的人物。……他性格中最为辉煌的部分是作为一位发明型数学天才的表现，其水准属第一流；这一点可从他的诸多发明和发现中看出，其中包括：通过无穷收敛级数对圆与双曲线的求积；他提出了曲线变换的方法；对布朗克勋爵用于平方双曲线的级数给出了几何证明；他证明了子午线与纬度余角一半的对数正切刻度相类比；他还利用双曲线发明并几何证明了一种非常简单的对数无穷收敛级数；他将著名的开普勒问题的解（以无穷级数形式）寄给柯林斯先生；他发现了一种几何作切线的方法，无需事先计算；他给出了一条关于正切的正、逆方法的法则，其基础与 “穷竭法” 上的流数学原理相同，且在应用方式上与之差别不大；他还提出了由切线求圆弧长度的级数，反之亦然；同样适用于正割、对数正切与对数正割的级数，反之亦然。这些成果，加上其他用于测量椭圆曲线与双曲线长度的方法，都被他寄给了柯林斯先生，以作为对柯林斯此前寄来的牛顿成果的回馈；在其中，他效仿牛顿这一优雅典范，将其级数以简单且互相独立的形式表述出来 $^\text{[17]}$。

5. 其他工作

　　在 1671 年写给约翰·柯林斯的信中，格里高利给出了七个函数的幂级数展开（使用现代符号）：$\arctan x $（通常称为格里高利级数），$\tan x$，$\sec x$， $\log \sec x$，反古德曼函数 $\log \tan \tfrac{1}{2}\left(x+\tfrac{1}{2}\pi\right)$，$\operatorname{arcsec}\!\left(\sqrt{2}e^x\right)$，以及古德曼函数 $2\arctan e^x - \tfrac{1}{2}\pi$$^\text{[18]}$

　　有证据表明，他发现了通过取高阶导数来计算幂级数的方法，而这一方法直到 1715 年才由泰勒正式提出。然而，格里高利并未发表相关成果，因为他认为自己不过是重新发现了 “牛顿先生的普遍方法”，尽管牛顿的方法基于的是另一种技术 $^\text{[19]}$。

　　詹姆斯·格里高利通过让阳光穿过鸟羽毛并观察产生的衍射图样，发现了光栅现象 $^\text{[20]}$。特别是他观察到了阳光分裂为各组成色彩——这一发现发生在牛顿用棱镜完成同样实验的一年之后，而当时这种现象仍然极具争议。

　　他认为圆形车轮不适合不规则表面，因此利用格里高利变换设计了一种合适的 “可适应车轮”$^\text{[21]}$。

　　格里高利是牛顿的热情支持者，后来与牛顿保持了许多友好的通信，并将牛顿的思想融入到自己的教学之中，而这些思想在当时被视为极具争议甚至相当革命性的。

　　月球上的 “格里高利陨石坑” 以他的名字命名。他还是数学家大卫·格里高利的叔叔。

6. 著作

1663 年 – Optica promota（《光学的进展》），Google 图书链接。
1667 年 – Vera circuli et hyperbolae quadratura（《圆与双曲线的真确求积》），互联网档案馆。
1668 年 – Exercitationes geometricae（《几何练习》），Google 图书链接。
1668 年 – Geometriae pars universalis（《几何学通论》）。

7. 另见

圣安德鲁斯的詹姆斯·格里高利望远镜
泰德天文台的格里高利望远镜
托马斯·里德
迪恩斯宫

8. 参考文献

Gregory, James (1668). Geometriae Pars Universalis. Museo Galileo: Patavii: typis heredum Pauli Frambotti.
William Johnston（学院副院长、数学教授，Centre College）；Alex McAllister（数学副教授，Centre College）（2009 年 6 月 26 日）。A Transition to Advanced Mathematics: A Survey Course。牛津大学出版社，第 329 页起。ISBN 978-0-19-971866-5。
Michael Nauenberg. Barrow and Leibniz on the fundamental theorem of the calculus.
Andrew Leahy. A Euclidean Approach to the FTC – Gregory's Proof of the FTC.
Ethan D. Bloch. The Real Numbers and Real Analysis，第 316 页。
Roger L. Cooke（2011 年 2 月 14 日）。The History of Mathematics: A Brief Course。John Wiley & Sons，第 467 页起。ISBN 978-1-118-03024-0。
D. J. Struik. A Source Book in Mathematics, 1200–1800。哈佛大学出版社，第 262 页起。ISBN 978-0-674-82355-6。
"Guild, Jean (bap. 1573, d. 1667), philanthropist". *Oxford Dictionary of National Biography*（在线版）。牛津大学出版社，2004 年。doi:10.1093/ref\:odnb/66919。2020 年 12 月 9 日检索。（需订阅、Wikipedia Library 访问或英国公共图书馆会员权限。）
Whiteside 2008，第 524 页。
"Scots scientist 'laid first meridian line' in St Andrews". BBC News，2014 年 10 月 3 日。检索于 2014 年 10 月 3 日。
Ceres Amson, John（2008 年 5 月）。"Gregory's meridian line of 1673–74: a St Andrews detective story". BSHM Bulletin: Journal of the British Society for the History of Mathematics。23 (2): 58–72. doi:10.1080/17498430802019804. S2CID 218589286.
Jean Montucla（1873）。History of the Quadrature of the Circle，J. Babin 译，William Alexander Myers 编，第 23 页，HathiTrust 链接。
W. W. Rouse Ball（1908）。A Short History of Mathematics，第四版。
D. R. Wilkins 抄本。
Robert Chambers, Thomas，《A Biographical Dictionary of Eminent Scotsmen》，第 175 页。
"Jim Cordes Big Dish". PBS. 存档于 2007 年 12 月 22 日。检索于 2007 年 11 月 22 日。
John Mason Good, Olinthus Gilbert Gregory, Newton Bosworth. *Pantologia: A new (cabinet) cyclopædia*（1813）。
Turnbull 1939，第 168–174 页。
Dehn, M.; Hellinger, E.（1943）。"Certain Mathematical Achievements of James Gregory". *American Mathematical Monthly*. 50 (3): 149–163. doi:10.2307/2302394. JSTOR 2302394.
Roy, Ranjan. "The Discovery of the Series Formula for (Pi) by Leibniz, Gregory and Nilakantha." Mathematics Magazine*, vol. 63, no. 5, 1990 年 12 月 1 日，第 291 页。
James Gregory 致 John Collins 的信，日期 1673 年 5 月 13 日。重印于：Correspondence of Scientific Men of the Seventeenth Century...，Stephen Jordan Rigaud 编辑（牛津：牛津大学出版社，1841），第 2 卷，第 251–255 页，特别是第 254 页。可在线获取：Books.Google.com。
Masurel, Christophe. "A generalization of the wheel or adaptable wheel " (PDF). 来源：christophe.masurel.free.fr。

9. 延伸阅读

Turnbull, Herbert Westren，编（1939）。James Gregory; Tercentenary Memorial Volume。G. Bell & Sons 出版，代表爱丁堡皇家学会出版。
Turnbull, Herbert Westren（1940–1941）。"Early Scottish Relations with the Royal Society: I. James Gregory, F.R.S. (1638–1675)"。Notes and Records of the Royal Society of London。3: 22–38. doi:10.1098/rsnr.1940.0003. JSTOR 531136. S2CID 145801030。
Malet, Antoni（1989）。Studies on James Gregorie (1638–1675)（博士论文）。普林斯顿大学。
Whiteside, D. T.（2008）。"Gregory (More Correctly Gregorie), James"。收录于 Charles Coulston Gillispie（编）。Dictionary of Scientific Biography。第 5 卷。纽约：Charles Scribner's Sons。第 524–530 页。检索于 2025 年 7 月 2 日。

10. 外部链接

Turnbull, H. W. (1938)。〈詹姆斯·格雷戈里诞辰三百周年纪念〉。检索于 2008 年 10 月 19 日。
O'Connor, John J.; Robertson, Edmund F.，，MacTutor 数学史档案，圣安德鲁斯大学。
詹姆斯·格雷戈里的欧几里得证明：微积分基本定理，载于 Convergence。
詹姆斯·格雷戈里宗教与科学公共讲座，圣安德鲁斯大学。
詹姆斯·格雷戈里《光学的推进》。
詹姆斯·格雷戈里《几何学通论部分》（The Universal Part of Geometry，Andrew Leahy 的英文译本，原著 Geometriae Pars Universalis）。存档于 2016 年 3 月 5 日，Wayback Machine。
詹姆斯·格雷戈里 (1663)《光学的推进》——林达·霍尔图书馆数字影印本。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。