约翰·彼得·古斯塔夫·勒热纳·狄利克雷（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科 相关文章。

　　 约翰·彼得·古斯塔夫·勒让·狄利克雷（Johann Peter Gustav Lejeune Dirichlet，/ˌdɪərɪˈkleɪ/\(^\text{[1]}\)，[德语发音：[ləˈʒœn diʁiˈkleː]\(^\text{[2]}\)；1805 年 2 月 13 日－1859 年 5 月 5 日）是德国数学家。在数论中，他证明了费马大定理的一些特殊情形，并创立了解析数论。在分析学中，他推进了傅里叶级数理论的发展，并且是最早给出函数现代形式定义的数学家之一。在数学物理中，他研究了势理论、边值问题、热扩散和流体力学。

　　 尽管他的姓氏是 “勒让·狄利克雷”，但在引用以他命名的成果时，人们通常只使用 “狄利克雷” 这一名字。

1. 生平

早年生活（1805–1822）

　　 古斯塔夫·勒让·狄利克雷于 1805 年 2 月 13 日出生在迪伦（Düren），这是位于莱茵河左岸的一座小镇，当时属于法兰西第一帝国，1815 年维也纳会议后归属普鲁士。他的父亲约翰·阿诺德·勒让·狄利克雷（Johann Arnold Lejeune Dirichlet）是一名邮政局长、商人及市议会议员。他的祖父则从比利时列日东北约 5 公里处的小村庄里舍莱特（Richelette，或更可能是 Richelle [fr]）迁居至迪伦，因此家族姓氏 “勒让·狄利克雷”（Lejeune Dirichlet，法语意为 “来自里舍莱特的年轻人”）由此而来。\(^\text{[3]}\)

　　 尽管家境并不富裕，而且狄利克雷在七个孩子中排行最小，父母仍然支持他的教育。他们先让他就读于一所小学，之后又转入私立学校，希望他日后能成为一名商人。然而年幼的狄利克雷在 12 岁之前就表现出了对数学的强烈兴趣，最终说服父母让他继续深造。1817 年，他被送往波恩文理中学（Gymnasium Bonn [de]）就读，受到家庭熟识的彼得·约瑟夫·埃尔韦尼希（Peter Joseph Elvenich，一位学生）的照顾。1820 年，狄利克雷转入科隆耶稣会文理中学，在那里他在乔治·欧姆的指导下，进一步拓宽了数学知识。次年他离开了文理中学，仅获得了一张结业证书，因为他无法流利使用拉丁语，未能取得正式的中学毕业文凭。\(^\text{[3]}\)

巴黎求学时期（1822–1826）

　　 狄利克雷再次说服了父母，为他的数学学习提供进一步的经济支持，尽管父母希望他从事法律事业。当时德国几乎没有学习高等数学的机会，唯一的例外是哥廷根大学的高斯，但高斯名义上是天文学教授，而且并不喜欢教学。因此，狄利克雷在 1822 年 5 月前往巴黎求学。在那里，他在法兰西公学院和巴黎大学听课，师从包括阿谢特在内的多位数学家，同时私下学习高斯的《算术研究》——这本书成为他终生随身携带的重要著作。 1823 年，经人推荐，狄利克雷受雇于马克西米连·福伊将军，担任其子女的私人德语教师。借此工作所得的报酬，狄利克雷终于实现了经济独立，不再需要依赖父母的资助。\(^\text{[4]}\)

　　 他的第一项原创研究是对费马大定理在 n= 5 情况下的部分证明，这项成果使他立刻声名鹊起——这是自费马本人完成 n= 4 情况的证明、以及欧拉完成 n= 3 情况的证明之后，该定理上的首次新进展。当时的审稿人之一勒让德很快完成了对 n= 5 情况的完整证明；不久后，狄利克雷也独立完成了自己的证明，并在几年后完成了对 n= 14 情况的完整证明。\(^\text{[5]}\)1825 年 6 月，他获准在法国科学院就 n= 5 情况的部分证明进行讲演——这对于一位年仅 20 岁、尚无学位的学生来说，是极其罕见的成就。\(^\text{[3]}\) 这次在科学院的讲座也使狄利克雷与傅里叶和泊松建立了联系，激发了他对理论物理学的兴趣，尤其是傅里叶的热传导解析理论。

返回普鲁士，布雷斯劳时期（1825–1828）

　　 1825 年 11 月，福伊将军去世，狄利克雷在法国也未能找到有报酬的职位，不得不返回普鲁士。傅里叶和泊松将他推荐给了亚历山大·冯·洪堡。当时洪堡受召加入普鲁士国王腓特烈·威廉三世的宫廷，正计划将柏林打造成科学研究中心。他立即向狄利克雷伸出援手，分别向普鲁士政府和普鲁士科学院写信推荐。同时，洪堡还为他争取到了高斯的推荐信。高斯在阅读了狄利克雷关于费马定理的论文后，给予了极高评价，称 “狄利克雷展现出极其出色的天赋”。\(^\text{[6]}\)

　　 在洪堡和高斯的支持下，狄利克雷获得了布雷斯劳大学的教职。不过，由于他尚未完成博士论文，便将自己关于费马定理的论文提交给波恩大学作为博士论文。然而，他缺乏拉丁语流利表达能力，无法进行论文要求的拉丁语公开答辩。经过多方讨论，波恩大学最终决定破例，于 1827 年 2 月授予他名誉博士学位。同时，教育部长也特批他豁免了进行博士资格答辩时所要求的拉丁语答辩。狄利克雷顺利获得博士资格认证，并于 1827–1828 学年在布雷斯劳以私人讲师身份授课。\(^\text{[3]}\)

　　 在布雷斯劳任教期间，狄利克雷继续从事数论研究，尤其是在双二次互反律方面做出了重要贡献——当时这是高斯研究的核心课题之一。洪堡借助狄利克雷这一系列的新成果（此时他也得到了天文学家贝塞尔的热烈赞誉），成功为他争取到转往柏林任教的机会。由于狄利克雷当时年纪尚轻（仅 23 岁），洪堡只为他在普鲁士军事学院争取到一个试用职位，同时名义上仍挂靠布雷斯劳大学。这一试用期被延长了三年，直到 1831 年该职位最终转为正式编制。

与蕾贝卡·门德尔松的婚姻

　　 狄利克雷搬到柏林后，洪堡将他介绍进了银行家亚伯拉罕·门德尔松·巴托尔迪（Abraham Mendelssohn Bartholdy）及其家族主办的著名沙龙。这座宅邸是柏林艺术家与科学家每周的聚会场所，其中包括亚伯拉罕的子女费利克斯·门德尔松（Felix Mendelssohn）与范妮·门德尔松（Fanny Mendelssohn）——两位杰出的音乐家——以及范妮的丈夫、画家威廉·亨塞尔（Wilhelm Hensel）。狄利克雷对亚伯拉罕的女儿蕾贝卡表现出浓厚兴趣，并于 1832 年与她结婚。

　　 蕾贝卡·亨丽埃特·勒让·狄利克雷（婚前名：蕾贝卡·门德尔松，1811 年 4 月 11 日—1858 年 12 月 1 日）是摩西·门德尔松的孙女，同时是费利克斯·门德尔松与范妮·门德尔松最小的妹妹。\(^\text{[7][8]}\) 蕾贝卡出生于汉堡。\(^\text{[9]}\)1816 年，她的父母为她安排了洗礼，自此起她改名为蕾贝卡·亨丽埃特·门德尔松·巴托尔迪。\(^\text{[10]}\) 她活跃于父母亚伯拉罕与莉娅·门德尔松的著名沙龙中，在德国思想界的高度活跃时期，与众多重要音乐家、艺术家和科学家交往甚密。1829 年，她在门德尔松家举办的费利克斯·门德尔松轻歌剧《异乡归来》首演中饰演了一个小角色。她后来曾写道：

　　 “我的哥哥姐姐们偷走了我作为艺术家的名声。在任何其他家庭，我都会被视为一名出色的音乐家，甚至可能领导一个乐团。而在费利克斯与范妮面前，我无法获得任何认可。”\(^\text{[11]}\)

　　 1832 年，她与狄利克雷结婚，狄利克雷正是通过洪堡介绍认识了门德尔松家族。\(^\text{[12]}\) 次年（1833 年），他们的长子瓦尔特出生。1858 年，她在哥廷根去世。

柏林时期（1826–1855）

　　 狄利克雷一到柏林便申请在柏林大学授课，教育部长批准了他的调动，并于 1831 年将他任命到哲学系任教。根据规定，学院要求他重新完成一次资格认证。虽然狄利克雷按要求撰写了资格论文，但他将必须用拉丁语进行的公开讲座一拖就是 20 年，直到 1851 年才完成。由于这一正式要求长期未完成，他在学院的职位一直不具备完全的职权，薪资也受到限制，被迫继续兼任军事学院的教职。1832 年，年仅 27 岁的狄利克雷成为普鲁士科学院的成员，是当时最年轻的院士。\(^\text{[3]}\)

　　 狄利克雷以讲解清晰而在学生中有很好的声誉，并且热爱教学，尤其是因为他在大学中讲授的往往是与他研究密切相关的高级课程：数论（他是德国第一位开设数论课程的教授）、分析学和数理物理学。他指导了多位重要德国数学家的博士论文，包括戈特霍尔德·艾森斯坦、利奥波德·克罗内克、鲁道夫·利普希茨和卡尔·威廉·博尔哈特，同时在许多其他科学家的数学教育中也发挥了重要影响，如克里斯托费尔、威廉·韦伯、海涅、冯·塞德尔和温加藤等。在军事学院，狄利克雷设法将微积分纳入课程体系，提升了该校的科学教育水平。然而，他也逐渐感到，在军事学院和大学的双重教学负担，正在限制他投入科研的时间。\(^\text{[3]}\)

　　 在柏林期间，狄利克雷与其他数学家保持联系。1829 年，在一次旅行中，他遇到了卡尔·雅可比，当时雅可比是哥尼斯堡大学的数学教授。几年间，他们持续会面并就研究问题进行通信，最终成为了亲密的朋友。1839 年，在一次访问巴黎时，狄利克雷遇到了约瑟夫·刘维尔，两位数学家很快成为朋友，保持联系，并在几年后互访并带着家人一起聚会。1839 年，雅可比将厄恩斯特·库默的论文寄给狄利克雷，库默当时是一位学校教师。狄利克雷意识到库默的潜力，便帮助他成功当选为柏林科学院院士，并在 1842 年为他争取到布雷斯劳大学的全职教授职位。1840 年，库默娶了奥蒂莉·门德尔松，她是狄利克雷妻子瑞贝卡的堂姐。

　　 1843 年，当雅可比生病时，狄利克雷前往哥尼斯堡帮助他，随后还为他争取到了普鲁士国王腓特烈·威廉四世的私人医生的帮助。当医生建议雅可比去意大利休养时，狄利克雷与家人一同陪同雅可比前往。路上，他们由路德维希·施拉夫利陪同，施拉夫利作为翻译同时也对数学产生了浓厚兴趣，狄利克雷和雅可比在旅途中给他讲授数学，施拉夫利后来也成为了重要的数学家。\(^\text{[3]}\) 狄利克雷一家将意大利的逗留延长至 1845 年，他们的女儿弗洛拉就是在意大利出生的。1844 年，雅可比作为皇室退休人员搬到柏林，他们的友谊变得更加亲密。1846 年，当海德堡大学试图招募狄利克雷时，雅可比向洪堡提供了必要的支持，使狄利克雷的薪水翻倍，从而使他留在柏林；然而，即使这样，狄利克雷依然没有拿到全职教授的薪水，且无法离开军事学院。\(^\text{[13]}\)

　　 持有自由主义观点的狄利克雷与家人支持 1848 年的革命；他甚至用步枪守卫普鲁士王子的宫殿。在革命失败后，军事学院暂时关闭，导致他失去了大量收入。学院重开后，环境变得对他更加敌对，因为他所教授的军官被要求忠诚于已成立的政府。一些没有支持革命的媒体把他与雅可比以及其他自由派教授列为 “红色阵营的成员”。\(^\text{[3]}\)

　　 1849 年，狄利克雷与他的朋友雅可比一同参与了高斯博士学位的纪念活动。

哥廷根时期（1855–1859）

　　 尽管狄利克雷在学术上的造诣深厚，也获得了诸多荣誉，而且到了 1851 年，他终于完成了全职教授所需的所有正式要求，但提高他在大学的薪资问题仍然被一拖再拖，他依旧无法脱离军事学院的工作。1855 年，高斯去世后，哥廷根大学决定邀请狄利克雷接任其职位。鉴于他在柏林所面临的诸多困难，狄利克雷决定接受邀请，并立即携家人迁往哥廷根。库默（Kummer）则被任命接替他在柏林的数学教授职位。\(^\text{[4]}\)

　　 狄利克雷非常享受在哥廷根的时光，较轻的教学任务使他有更多时间投入科研工作，并与新一代研究者建立了密切联系，尤其是理查德·戴德金和伯恩哈德·黎曼。他到哥廷根后，还设法为黎曼争取到一份小额年薪，使其能留在教师队伍中。尽管戴德金、黎曼、莫里茨·康托尔（Moritz Cantor）和阿尔弗雷德·恩内珀（Alfred Enneper）都已获得博士学位，但他们仍前来听狄利克雷授课，向他学习。戴德金自认为在数学教育上存在不足，称能跟随狄利克雷学习使他 “仿佛重获新生”。\(^\text{[3]}\) 他后来整理并出版了狄利克雷关于数论的讲义与其他成果，命名为《数论讲义》。

　　 1858 年夏天，在蒙特勒旅行期间，狄利克雷突发心脏病。1859 年 5 月 5 日，他在哥廷根去世，距其妻瑞贝卡去世仅数月之隔。\(^\text{[4]}\) 狄利克雷的大脑如今保存在哥廷根大学生理学系，和高斯的大脑一起存放。。柏林科学院在 1860 年为他举行了正式的追悼会，由库默致悼词，随后委托克罗内克与拉撒路·福克斯编辑并出版了他的全集。

2. 数学研究

数论

　　 数论是狄利克雷的主要研究领域，\(^\text{[14]}\) 在这一领域他取得了多项重要成果，并在证明过程中引入了许多基本工具，其中不少后来以他的名字命名。1837 年，狄利克雷在证明等差数列中的素数定理时，首次运用数学分析中的概念来处理代数问题，从而奠定了解析数论这一分支学科的基础。在该定理的证明中，他引入了狄利克雷特征与狄利克雷 L 函数。\(^\text{[14][15]}\) 在这篇论文中，他还注意到了级数的绝对收敛与条件收敛之区别，以及这一性质对后来的黎曼级数定理所产生的影响。1841 年，他将等差数列定理从整数推广到高斯整数环 $\mathbb{Z}[i]$。\(^\text{[3]}\)

　　 在 1838 年和 1839 年的两篇论文中，他首次证明了二次型的类数公式（后来由他的学生克罗内克作了进一步完善）。雅可比曾称该公式为 “几近人类智慧巅峰的成果”。该公式为更一般的数域上的类似研究开辟了道路。\(^\text{[3]}\) 在研究二次域单位群结构的基础上，他证明了狄利克雷单位定理，这一结果成为代数数论中的基础定理之一。\(^\text{[15]}\)

　　 他在证明丢番图逼近中的一个定理时，首次使用了如今被称为抽屉原理的基本计数方法，该定理后来被称为狄利克雷逼近定理。他还对费马大定理做出了重要贡献，证明了 $n=5$ 和 $n=14$ 的情形，并在双二次互反律方面发表了重要成果。\(^\text{[3]}\) 此外，在研究狄利克雷除数问题时，他引入了著名的狄利克雷双曲法并得出了初步结果。\(^\text{[16]}\) 尽管后续数学家不断推进，这一问题至今仍未被完全解决。

分析学

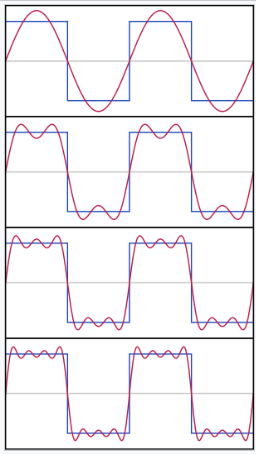
　　 受他在巴黎的导师研究的启发，狄利克雷于 1829 年发表了一篇著名的论文，首次明确给出了傅里叶级数收敛的条件，指出了哪些函数的傅里叶级数是收敛的。\(^\text{[17]}\) 在狄利克雷的成果发表之前，不仅傅里叶本人，连泊松和柯西都未能成功给出严谨的收敛性证明。狄利克雷在论文中指出了柯西证明中的错误，并提出了著名的狄利克雷判别法来检验级数的收敛性。

　　 在这篇论文中，他还引入了狄利克雷函数，这是一个无法积分的函数例子（当时不定积分和定积分理论尚在发展中）。在傅里叶级数的证明过程中，他提出了狄利克雷核和狄利克雷积分等重要概念。\(^\text{[18]}\)

　　 此外，狄利克雷还研究了拉普拉斯方程的一类第一边值问题（即在边界上给定函数值的情形），并证明了其解的唯一性。后来，这类偏微分方程的边值问题被命名为狄利克雷问题以纪念他的贡献。\(^\text{[14]}\) 在证明过程中，他巧妙运用了这样一个变分原理：问题的解是最小化狄利克雷能量的函数。后来，黎曼将这种方法命名为狄利克雷原理，尽管黎曼也知道高斯和开尔文勋爵在此之前也曾用过类似的思路。\(^\text{[3]}\)

引入现代函数概念

　　 在试图确定傅里叶级数可以收敛的函数范围时，狄利克雷将函数定义为 “对于任意的 $x$，都对应着一个有限的 $y$”，但随后又将注意力集中在分段连续函数上。基于此，他被认为首次引入了现代意义上的函数概念，这一区别于早期将函数模糊地理解为某种解析公式的做法。\(^\text{[3]}\) 伊姆雷·拉卡托什引用赫尔曼·汉克尔作为最早持有这一观点的人，但他对该说法持异议，指出 “有大量证据表明狄利克雷本人并没有真正掌握这一概念……例如，当他讨论分段连续函数时，曾表示在不连续点，函数具有两个值”。\(^\text{[19]}\)

其他领域

　　 狄利克雷还在数学物理领域有所建树，曾在势理论（包括上文提到的狄利克雷问题和狄利克雷原理）、热传导理论以及流体力学方面授课和发表研究成果。$14$ 他对拉格朗日关于保守系统的研究做出了改进，指出平衡的条件是势能取得最小值。\(^\text{[20]}\)

　　 狄利克雷还讲授过概率论与最小二乘法，在极限定理及中心极限定理相关的拉普拉斯近似方法方面提出了原创性方法与改进成果。\(^\text{[21]}\) 以他的名字命名的有狄利克雷分布与狄利克雷过程，它们均基于狄利克雷积分而得名。

3. 荣誉

　　 狄利克雷被多所科学院选为院士成员：\(^\text{[22]}\)

• 普鲁士科学院（1832 年）
• 圣彼得堡科学院（1833 年）——通讯院士
• 哥廷根科学院（1846 年）
• 法国科学院（1854 年）——外籍院士
• 瑞典皇家科学院（1854 年）
• 比利时皇家科学院（1855 年）
• 英国皇家学会（1855 年）——外籍院士

　　 1855 年，经亚历山大·冯·洪堡推荐，狄利克雷被授予 “为功勋” 勋章的平民等级勋章。月球上的狄利克雷环形山和小行星 11665 Dirichlet 均以他的名字命名。

4. 主要出版物

• Lejeune Dirichlet, J.P.G. (1889). 由 L. Kronecker 编辑，《著作集》第一卷，柏林：Reimer 出版社。
• Lejeune Dirichlet, J.P.G. (1897). 由 L. Kronecker 和 L. Fuchs 编辑，《著作集》第二卷，柏林：Reimer 出版社。
• Lejeune Dirichlet, J.P.G.; Richard Dedekind (1863). 《数论讲义》，F. Vieweg und Sohn 出版社。

　　 狄利克雷所有已发表作品（包括译本及未收入《著作集》的讲义）可参考下列完整文献目录：

• Merzbach, Uta C. (2018). *Dirichlet: A Mathematical Biography*. Springer. doi:10.1007/978-3-030-01073-7. ISBN 978-3-030-01071-3. MR 3887586. Zbl 1412.01003.

5. 参考文献

1. "Dirichlet". Random House Webster's Unabridged Dictionary*.
2. Dudenredaktion (2015). *Duden – Das Aussprachewörterbuch: Betonung und Aussprache von über 132.000 Wörtern und Namen* [杜登发音词典：132,000 多个词汇和姓名的重音与发音]（德语）. Duden - Deutsche Sprache in 12 Bänden. 第 6 卷，第 312 页. ISBN 978-3-411-91151-6.
3. Elstrodt, Jürgen (2007). "The Life and Work of Gustav Lejeune Dirichlet (1805–1859)" (PDF). *Clay Mathematics Proceedings*. 2007 年 12 月 25 日检索.
4. James, Ioan Mackenzie (2003). *Remarkable Mathematicians: From Euler to von Neumann*. 剑桥大学出版社. 第 103–109 页. ISBN 978-0-521-52094-2.
5. Krantz, Steven (2011). *The Proof is in the Pudding: The Changing Nature of Mathematical Proof*. Springer. 第 55–58 页. ISBN 978-0-387-48908-7.
6. Goldstein, Cathérine; Catherine Goldstein; Norbert Schappacher; Joachim Schwermer (2007). *The shaping of arithmetic: after C.F. Gauss's Disquisitiones Arithmeticae*. Springer. 第 204–208 页. ISBN 978-3-540-20441-1.
7. Mercer-Taylor, Peter. *The Life of Mendelssohn*. 剑桥，2000 年. ISBN 978-0-521-63972-9.
8. Todd, R. Larry. *Mendelssohn: A Life in Music*. 牛津，2003 年. ISBN 978-0-19-511043-2.
9. Todd 2003，第 28 页。
10. Todd 2003，第 33 页。
11. 引自 Mercer-Taylor 2000，第 66 页。
12. Todd 2003，第 192 页。
13. Calinger, Ronald (1996). *Vita mathematica: historical research and integration with teaching*. 剑桥大学出版社. 第 156–159 页. ISBN 978-0-88385-097-8.
14. Gowers, Timothy; June Barrow-Green; Imre Leader (2008). *The Princeton companion to mathematics*. 普林斯顿大学出版社. 第 764–765 页. ISBN 978-0-691-11880-2.
15. Kanemitsu, Shigeru; Chaohua Jia (2002). *Number theoretic methods: future trends*. Springer. 第 271–274 页. ISBN 978-1-4020-1080-4.
16. Dirichlet, Peter Gustav Lejeune (1849). "Über die Bestimmung der mittleren Werthe in der Zahlentheorie". *Abhandlungen der Königlich Preussischen Akademie der Wissenchaften*（德语）: 第 49–66 页 — 通过 Gallica 获取。
17. Lejeune Dirichlet (1829). "Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données" [关于用于表示给定区间内任意函数的三角级数的收敛性]. *Journal für die reine und angewandte Mathematik*. 第 4 卷：157–169 页。
18. Bressoud, David M. (2007). *A radical approach to real analysis*. MAA. 第 218–227 页. ISBN 978-0-88385-747-2.
19. Lakatos, Imre (1976). *Proofs and refutations: the logic of mathematical discovery*. 剑桥大学出版社. 第 151–152 页. ISBN 978-0-521-29038-8.
20. Leine, Remco; Nathan van de Wouw (2008). *Stability and convergence of mechanical systems with unilateral constraints*. Springer. 第 6 页. ISBN 978-3-540-76974-3.
21. Fischer, Hans (1994 年 2 月). "Dirichlet's contributions to mathematical probability theory". *Historia Mathematica*. 21 (1). Elsevier: 39–63 页. doi:10.1006/hmat.1994.1007.
22. "Obituary notices of deceased fellows". *Proceedings of the Royal Society of London*. 第 10 卷. Taylor and Francis: xxxviii–xxxix. 1860 年. doi:10.1098/rspl.1859.0002. S2CID 186209363.

6. 外部链接

• 维基共享资源中与彼得·古斯塔夫·勒让·狄利克雷相关的多媒体资源
• O'Connor, John J.; Robertson, Edmund F., "Peter Gustav Lejeune Dirichlet", MacTutor 数学史档案*，圣安德鲁斯大学
• Elstrodt, Jürgen (2007). "古斯塔夫·勒让·狄利克雷 (1805–1859) 的生平与工作"（PDF 文件），Clay Mathematics Proceedings，2010 年 6 月 13 日访问
• 数学家世系项目中的彼得·古斯塔夫·勒让·狄利克雷资料
• Johann Peter Gustav Lejeune Dirichlet – 全集 – Gallica-Math