魏尔施特拉斯函数（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科 相关文章。

　　 在数学中，魏尔施特拉斯函数以其发现者卡尔·魏尔施特拉斯的名字命名，是一个实值函数的典型例子，它在所有点上都是连续的，但却在任何一点都不可导。它也是分形曲线的一个例子。

　　 魏尔施特拉斯函数在历史上被视为一种 “反常函数”，它是第一个被明确构造出来、用于挑战 “每个连续函数除了在一些孤立点外都可导” 这一观念的例子（发表于 1872 年）\(^\text{[1]}\)。魏尔施特拉斯通过这个函数展示了连续性并不意味着 “几乎处处可导”，这一点颠覆了数学界的传统看法，也推翻了许多依赖几何直觉和模糊 “光滑性” 定义的证明。彼时的数学家普遍不喜欢这类函数：查尔斯·埃尔米特在发现自己研究的一类函数也具备这种性质时，曾称其为 “令人悲哀的灾难”\(^\text{[2]}\)。在计算机出现之前，这类函数难以直观地想象，其结果也未被广泛接受，直到后来出现了实际应用场景，例如对布朗运动的建模，这类 “无限锯齿状” 的函数才变得必要（如今称为分形曲线）\(^\text{[3]}\)。

1. 构造方法

　　 在魏尔斯特拉斯的原始论文中，这个函数被定义为一个傅里叶级数： $$ f(x) = \sum_{n=0}^{\infty} a^n \cos\left(b^n \pi x\right) ~ $$ 其中 $0 < a < 1$、 $b$ 是一个正的奇整数，且满足条件： $$ ab > 1 + \frac{3}{2}\pi~ $$ 对于满足上述条件的 $0 < a < 1$，使得不等式成立的最小整数 $b$ 是 $b = 7$。这一构造方式以及证明该函数在任意点处都不可导的论证，最早由魏尔斯特拉斯于 1872 年 7 月 18 日在普鲁士皇家科学院提交的论文中提出 \(^\text{[4][5][6]}\)。

　　 尽管魏尔斯特拉斯函数在任何点都不可导，但它是连续的：这是因为定义它的无穷级数中的每一项都被 $\pm a^n$ 所有界，而当 $0 < a < 1$ 时，该级数的总和是有限的。根据魏尔斯特拉斯判别法（Weierstrass M-检验），设 $M_n = a^n$，则该级数一致收敛。由于每一部分和都是连续函数，根据一致极限定理，可以推出函数 $f$ 是连续的。此外，由于每一部分和都是一致连续的，所以 $f$ 也是一致连续的。

　　 人们原本可能会认为，连续函数一定可导，或至少其不可导点的集合应该是有限的或可数无穷的。魏尔斯特拉斯在论文中指出，早期的数学家（包括高斯）通常都默认这种观点成立。这可能是因为，人们很难描绘或直观想象出一个在不可数集合上不可导的连续函数。而对于 “行为良好” 的连续函数类别，确实存在类似的结果，例如：Lipschitz 函数的不可导点集必须是勒贝格零测集（这由拉德马赫定理 Rademacher's Theorem 给出）。我们通常画出的函数图像大多是 Lipschitz 的，或其他 “良性” 函数。因此，魏尔斯特拉斯函数中快速震荡的行为，是其处处不可导的重要原因——例如，对于单调函数，其不可导点集是零测集，而魏尔斯特拉斯函数正是通过剧烈震荡避免这一限制。

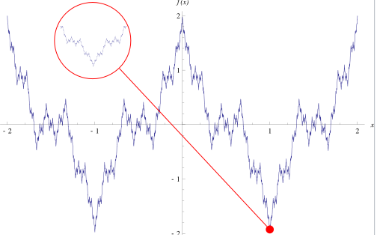
　　 魏尔斯特拉斯函数是最早被研究的分形之一，尽管 “分形” 这一术语要到很久之后才被提出。这个函数在任意尺度下都具有细节特征，所以即使放大它的任意一小段，也不会越来越接近直线。在任意两个非常接近的点之间，它都不是单调的。

　　 该函数图像的 Hausdorff 维数 $D$ 的计算一直是一个未解问题，直到 2018 年才被彻底解决。此前人们普遍认为 $D = 2 + \log_b(a) < 2$。\(^\text{[7][8] }\) 从前文对 $a$ 和 $b$ 的约束条件可以推出 $D < 2$。然而，这个结论在理论上花了超过 30 年的时间才被严格证明。\(^\text{[9]}\)

　　 “魏尔斯特拉斯函数” 这个术语在实分析中常泛指所有具有类似构造和性质的函数。例如，在无穷级数中将余弦函数替换为分段线性的 “锯齿形” 函数，也能得到类似的处处不可导函数。G.H. 哈代（G. H. Hardy）证明：只要满足 $0 < a < 1$，且 $ab \geq 1$，上述构造出的函数就是处处不可导的。\(^\text{[10]}\)

2. 黎曼函数

　　 魏尔斯特拉斯函数是基于更早的**黎曼函数**构造的，黎曼声称该函数在任何一点都不可导。该函数有时也被称为魏尔斯特拉斯函数： $$ f(x) = \sum_{n=1}^{\infty} \frac{ \sin\left(n^2 x\right) }{n^2}~ $$ 尽管伯恩哈德·黎曼（Bernhard Riemann）坚称这个函数在任何点都不可导，但他并没有发表任何相关证明。魏尔斯特拉斯指出，他在黎曼的文稿中或从黎曼学生的口述中都没有找到这种主张的证据。

　　 1916 年，G.H. 哈代（G. H. Hardy）证明该函数在如下类型的点没有有限导数：当 $x$ 是无理数，或是形如 $\frac{2A}{4B+1}$ 或 $\frac{2A+1}{2B}$ 的有理数时（其中 $A, B$ 为整数）\(^\text{[10]}\)。1969 年，约瑟夫·格尔弗发现，当 $x$ 是形如 $\frac{2A+1}{2B+1}\pi$ 的点（即 $\pi$ 的有理倍数，分子分母均为奇数）时，黎曼函数在这些点上是可导的，其导数为：$f'(x) = -\frac{1}{2}$1971 年，格尔弗又证明：当 $x$ 是形如 $\frac{2A}{2B+1}\pi$ 的点时，黎曼函数在这些点上没有有限导数，至此，黎曼函数的可导性问题被完整解决。\(^\text{[13]}\)

　　 由于黎曼函数仅在一个勒贝格零测集上可导，它几乎处处不可导。

3. 赫尔德连续性

　　 魏尔斯特拉斯函数也可以等价地写作： $$ W_\alpha(x) = \sum_{n=0}^{\infty} b^{-n\alpha} \cos\left(b^n \pi x\right) ~ $$ 其中 $\alpha = -\frac{ \ln\left(a\right) }{ \ln\left(b\right) }$ 此时，函数 $W_\alpha(x)$ 是 $\alpha$ 阶赫尔德连续的，也就是说，存在一个常数 $C$，使得对所有的 $x$ 和 $y$ 都有： $$ |W_\alpha(x) - W_\alpha(y)| \leq C |x - y|^\alpha~ $$ 此外，$W_1$ 是对所有 $\alpha < 1$ 都赫尔德连续的，但不满足利普希茨连续性。

4. 无处可导函数的稠密性

　　 事实证明，魏尔斯特拉斯函数远不是一个孤例：虽然它被称为 “反常” 的例子，但从某种意义上说，它也是连续函数中的 “典型” 代表：

• 从拓扑意义上说：在以一致收敛拓扑构成的向量空间 $C([0, 1]; \mathbb{R})$（即定义在 [0, 1] 上的所有实值连续函数的集合）中，无处可导函数的集合是 comeager 的，也就是说，它们在拓扑意义上占据 “多数”。[15][16]
• 从测度论意义上说：当 $C([0, 1]; \mathbb{R})$ 上赋予经典的 维纳测度 $\gamma$ 时，在 [0, 1] 上哪怕仅在一点处可导的函数集合的测度也为零。即使在 $C([0, 1]; \mathbb{R})$ 的有限维 “切片” 中，这种情况依然成立——无处可导函数构成其中的一个广泛存在的子集。

5. 参见

• 布朗芒曲线
• 科赫雪花
• 无处连续函数

6. 注释

1. 早在魏尔斯特拉斯之前，至少有两位研究者构造出了连续但处处不可导的函数，但他们的成果在生前未曾发表：约 1831 年，捷克数学家、哲学家兼天主教神父 伯纳德·博尔查诺（Bernard Bolzano, 1781–1848）构造了这样一个函数。然而，该函数直到 1922 年** 才首次发表。参见：
   • Martin Jašek (1922)《Bolzano 函数》（捷克语与德语），发表于《数学与物理发展杂志》Vol. 51, No. 2, 页 69–76。
   • Vojtěch Jarník (1922)《关于 Bolzano 函数》，同刊 Vol. 51, No. 4, 页 248–264。[捷克语原文在线版本](http://dml.cz/bitstream/handle/10338.dmlcz/109021/CasPestMatFys_051-1922-4_5.pdf)[英文翻译版本](http://dml.cz/bitstream/handle/10338.dmlcz/400073/Bolzano_15-1981-1_6.pdf)
   • Karel Rychlík (1923)《关于 Bolzano 手稿遗稿中的一个函数》（德语），发表于《布拉格皇家波希米亚科学院年报》（1921–1922），第 II 类，第 4 期，页 1–20。大约 1860 年，日内瓦大学教授 夏尔·塞勒里耶（Charles Cellérier, 1818–1889）独立构造出了一个与魏尔斯特拉斯函数非常相似的连续处处不可导函数。该成果于其身后发表：
   • Cellérier, C. (1890)《关于分析基本原理的笔记》，发表于《数学科学通报》（第二系列），Vol. 14, 页 142–160。
2. 相关书信记录也说明了当时的数学家对这种函数的反感： Hermite, Charles; Stieltjes, Thomas (1905). 《第 374 封信，1893 年 5 月 20 日》，见 Benjamin Baillaud 与 Henri Bourget 编，《Hermite 与 Stieltjes 书信集》，Vol. 2，Gauthier-Villars 出版社，页 317–319。
3. 有关这些 “怪物函数” 的现代叙述： Adam Kucharski（2017 年 10 月 26 日）《数学的美丽怪兽：一种颠覆性理念如何铺就现代数学之路》，于 2023 年 10 月 11 日访问。
4. 在《1872 年柏林皇家普鲁士科学院月报》第 560 页中，有一则简短的记录提到，在 7 月 18 日，“Weierstrass 先生朗读了一篇关于**处处连续但无明确导数的函数**的论文”（原文：“Hr. Weierstrass las über stetige Funktionen ohne bestimmte Differentialquotienten”）。然而，魏尔斯特拉斯的这篇论文并未刊载于该期月报中。 相关文献：
5. Karl Weierstrass，《关于某个实变量的连续函数在任何取值处都不具有确定导数的情况》（德文原名："Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzteren einen bestimmten Differentialquotienten besitzen"），载于《柏林皇家普鲁士科学院：Karl Weierstrass 数学论文集》（Mathematische Werke von Karl Weierstrass），第 2 卷，第 71–74 页，出版：德国柏林 Mayer & Müller，1895 年。 另见：
6. Karl Weierstrass，《函数论论文集》（Abhandlungen aus der Functionenlehre），柏林：Julius Springer 出版社，1886 年，第 97 页。
7. Kenneth Falconer，《分形集合的几何学》（The Geometry of Fractal Sets），剑桥大学出版社，1985 年，第 114 页、第 149 页。
8. 另见：Brian R. Hunt (1998)，《魏尔斯特拉斯函数图像的 Hausdorff 维数》（"The Hausdorff dimension of graphs of Weierstrass functions"），载于《美国数学会会刊》（Proceedings of the American Mathematical Society），第 126 卷第 3 期，第 791–800 页。
9. 沈维孝 (2018)，《经典魏尔斯特拉斯函数图像的 Hausdorff 维数》，载于《数学杂志》（Mathematische Zeitschrift），第 289 卷第 1–2 期，第 223–266 页，arXiv:1505.03986，doi:10.1007/s00209-017-1949-1。
10. G.H. Hardy (1916)，《魏尔斯特拉斯的不可导函数》，载于《美国数学会会刊》（Transactions of the American Mathematical Society），第 17 卷，第 301–325 页。
11. Weisstein, Eric W. “魏尔斯特拉斯函数”。MathWorld 网站。
12. Gerver, Joseph（1969 年）。“黎曼函数在某些 π 的有理倍数处的可导性”，载于《美国国家科学院院刊》（Proceedings of the National Academy of Sciences of the United States of America），第 62 卷第 3 期，第 668–670 页。Bibcode:1969PNAS...62..668G，doi:10.1073/pnas.62.3.668，PMC 223649，PMID 16591735。
13. Gerver, Joseph（1971 年）。“关于黎曼函数可导性的进一步探讨”，载于《美国数学杂志》（American Journal of Mathematics），第 93 卷第 1 期，第 33–41 页，doi:10.2307/2373445，JSTOR 2373445，S2CID 124562827。
14. Zygmund, A.（2002 年，初版 1935 年）。《三角级数》（Trigonometric Series），剑桥数学文库（Cambridge Mathematical Library），第 I、II 卷（第 3 版），剑桥大学出版社，第 47 页，ISBN 978-0-521-89053-3，MR 1963498。
15. Mazurkiewicz, S.（1931 年）。“关于不可导函数”（Sur les fonctions non-dérivables），载于《数学研究》（Studia Mathematica），第 3 卷第 3 期，第 92–94 页，doi:10.4064/sm-3-1-92-94。
16. Banach, S.（1931 年）。“关于某些函数集的 Baire 范畴”（Über die Baire'sche Kategorie gewisser Funktionenmengen），载于《数学研究》（Studia Mathematica），第 3 卷第 3 期，第 174–179 页，doi:10.4064/sm-3-1-174-179。

7. 参考文献

• David, Claire（2018 年），“绕过动力系统：一种简单方法获取魏尔斯特拉斯函数图像的盒维数”，载于《国际几何中心会刊》，第 11 卷第 2 期，乌克兰科学院，第 53–68 页，arXiv:1711.10349，doi:10.15673/tmgc.v11i2.1028。
• Falconer, K.（1984 年），《分形集的几何学》，剑桥数学论丛，第 85 卷，剑桥：剑桥大学出版社，ISBN 978-0-521-33705-2。
• Gelbaum, B Bernard R.; Olmstead, John M. H.（2003 年，[初版 1964 年]），《分析中的反例》，多佛数学丛书，多佛出版公司，ISBN 978-0-486-42875-8。
• Hardy, G. H.（1916 年），“魏尔斯特拉斯不可导函数”，载于《美国数学学会汇刊》（Transactions of the American Mathematical Society），第 17 卷第 3 期，美国数学学会，第 301–325 页，doi:10.2307/1989005，JSTOR 1989005（[PDF 格式]）。
• Weierstrass, Karl（1872 年 7 月 18 日），《关于某一实变量的连续函数，其在任意一点都不具有确定的导数》，普鲁士皇家科学院。
• Weierstrass, Karl（1895 年），“关于某一实变量的连续函数，其在任意一点都不具有确定的导数”，收录于《魏尔斯特拉斯数学文集》，第 2 卷，德国柏林：Mayer & Müller 出版社，第 71–74 页。
• 英文译本：Edgar, Gerald A.（1993 年），《关于某一实变量的连续函数，其在任意点都不具有良定义的导数》，收录于《分形经典文献选》，非线性研究丛书，爱迪生-韦斯利出版公司，第 3–9 页，ISBN 978-0-201-58701-2。

8. 外部链接

• Weisstein, Eric W. “魏尔斯特拉斯函数”。MathWorld。（一种不同的魏尔斯特拉斯函数，也具有连续但处处不可导的性质）
• 使用巴拿赫不动点原理证明连续处处不可导函数存在性的论证。
• 使用贝尔范畴定理证明处处不单调连续函数存在性的论证。
• Johan Thim. “连续但处处不可导的函数”（Continuous Nowhere Differentiable Functions）。吕勒奥理工大学硕士论文，2003 年。存档于 2017 年 2 月 22 日[原文]，检索日期：2006 年 7 月 28 日。
• 复平面中的魏尔斯特拉斯函数（Weierstrass function in the complex plane），存档于 2009 年 9 月 24 日，[原文]，展现出精美的分形图案。
• SpringerLink - 《傅里叶分析与应用期刊》第 16 卷第 1 期：魏尔斯特拉斯函数及其缓慢增长情形的处处不可导性简单证明。
• 魏尔斯特拉斯函数：连续但在任意一点都不可导。
• 伯克利大学 Brent Nelson 撰写的《魏尔斯特拉斯函数》一文，展示其不可导性特征。