泰勒斯定理（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

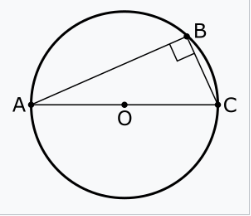
　　 在几何学中，塔勒斯定理指出，如果 \(A\)、\(B\) 和 \(C\) 是圆上的不同点，其中 \(\overline{AC}\) 是直径，则角 \(\angle ABC\) 是直角。塔勒斯定理是内切角定理的一个特例，并作为欧几里得《几何原本》第三卷第 31 命题的一部分被提及和证明。[1] 通常认为该定理归功于米利都的塔勒斯，但有时也归功于毕达哥拉斯。

1. 历史

　　 巴比伦数学家在希腊数学家证明之前，就已经知道这个定理的特殊情况。[2]

　　 米利都的泰勒斯（公元前 6 世纪初）传统上被认为是第一个证明该定理的人；然而，到了公元前 5 世纪，泰勒斯的著作已不复存在，后来的历史学家根据听说和推测，将许多发明和思想归于泰勒斯和毕达哥拉斯等智慧人物。[3][4] 普罗克鲁斯（公元 5 世纪）和狄奥根尼·拉厄尔修（公元 3 世纪）都提到了泰勒斯，并且记录了帕姆菲拉（公元 1 世纪）的话，称泰勒斯 “是第一个在圆内刻画直角三角形的人”。[5]

　　 据说泰勒斯曾前往埃及和巴比伦，在那里他学到了几何学和天文学的知识，并将这些知识带回希腊，途中发明了几何证明的概念，并证明了各种几何定理。然而，没有直接证据支持这些说法，它们很可能是后来的推测性合理化。现代学者认为，希腊的演绎几何学（如欧几里得《几何原本》中的几何学）直到公元前 4 世纪才发展起来，而泰勒斯所掌握的任何几何知识很可能只是观察性的。[3][6]

　　 该定理出现在欧几里得《几何原本》第三卷（公元前 300 年左右）的第 31 命题中：“在圆中，半圆内的角是直角，较大弧段中的角小于直角，较小弧段中的角大于直角；此外，较大弧段的角大于直角，较小弧段的角小于直角。”

　　 但丁·阿利吉耶里的《神曲·天堂篇》（第 13 歌，101-102 行）在一段演讲中提到了泰勒斯定理。

2. 证明

第一次证明

　　 以下事实被使用：三角形内角和等于 180°，等腰三角形的底角相等。

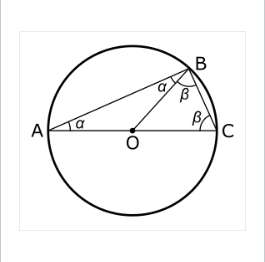
　　 由于 \(\overline{OA} = \overline{OB} = \overline{OC}\)，△OBA 和 △OBC 是等腰三角形，并且根据等腰三角形底角相等的性质，\(\angle OBC= \angle OCB\) 且 \(\angle OBA = \angle OAB\)。

　　 设 \(\alpha = \angle BAO\) 和 \(\beta = \angle OBC\)。\(\triangle ABC\) 三角形的三个内角分别是 \(\alpha\)、\((\alpha + \beta)\) 和 \(\beta\)。由于三角形内角和等于 180°，我们有： \[ \alpha + (\alpha + \beta) + \beta = 180^\circ~ \] \[ 2\alpha + 2\beta = 180^\circ~ \] \[ 2(\alpha + \beta) = 180^\circ~ \] \[ \therefore \alpha + \beta = 90^\circ.~ \] 证毕。

第二次证明

　　 该定理也可以通过三角学来证明：设 \( O = (0, 0) \)，\( A = (-1, 0) \)，\( C = (1, 0) \)。然后 \( B \) 是单位圆上的一点 \((\cos \theta, \sin \theta)\)。我们将通过证明 \(\overline{AB}\) 和 \(\overline{BC}\) 是垂直的来展示 \(\triangle ABC\) 形成直角——即它们的斜率的乘积等于 -1。我们计算 \(\overline{AB}\) 和 \(\overline{BC}\) 的斜率： \[ m_{AB} = \frac{y_B - y_A}{x_B - x_A} = \frac{\sin \theta}{\cos \theta + 1}~ \] \[ m_{BC} = \frac{y_C - y_B}{x_C - x_B} = \frac{-\sin \theta}{-\cos \theta + 1}~ \] 然后我们证明它们的乘积等于 -1： \[ m_{AB} \cdot m_{BC} = \frac{\sin \theta}{\cos \theta + 1} \cdot \frac{-\sin \theta}{-\cos \theta + 1}~ \] \[ = \frac{-\sin^2 \theta}{-\cos^2 \theta + 1}~ \] \[ = \frac{-\sin^2 \theta}{\sin^2 \theta}~ \] \[ = -1~ \] 注意使用了毕达哥拉斯三角恒等式：\(\sin^2 \theta + \cos^2 \theta = 1\).

第三次证明

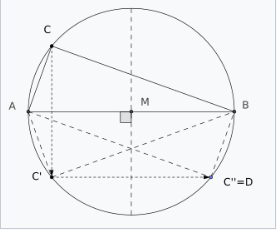
　　 设 \(\triangle ABC\) 为圆中的一个三角形，其中 \(AB\) 是该圆的直径。然后通过先沿直线 AB 反射 \(\triangle ABC\)，再沿通过圆心且垂直于 \(AB\) 的直线进行第二次反射，构造一个新的三角形 \(\triangle ABD\)。由于 \(AC\) 和 \(BD\) 是平行的，同样 \(AD\) 和 \(CB\) 也是平行的，四边形 \(ABCD\) 是平行四边形。由于 \(AB\) 和 \(CD\) 是平行四边形的对角线，且它们都是圆的直径，因此长度相等，所以这个平行四边形必须是矩形。矩形中的所有角都是直角。

3. 逆命题

　　 对于任何三角形，特别是任何直角三角形，存在一个唯一的圆包含三角形的所有三个顶点。这个圆称为三角形的外接圆。

　　 塔勒斯定理的一个表述方式是：如果三角形外接圆的圆心位于三角形内部，则该三角形是直角三角形，并且其外接圆的圆心位于斜边上。

　　 塔勒斯定理的逆命题是：直角三角形的外接圆圆心位于其斜边上。（等价地，直角三角形的斜边是其外接圆的直径。）

使用几何学证明逆命题

　　 这个证明通过 “补全” 直角三角形形成一个矩形，并注意到矩形的中心距离所有顶点的距离相等，因此它是原三角形外接圆的圆心。该证明利用了两个事实：

1. 平行四边形的邻角互为补角（加起来等于 180°）；
2. 矩形的对角线相等并在其中点交汇。

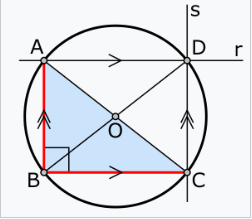
　　 设 \(\angle ABC\) 为直角，\(r\) 为通过 \(A\) 且平行于 \(\overline{BC}\) 的直线，\(s\) 为通过 \(C\) 且平行于 \(\overline{AB}\) 的直线。设 \(D\) 为直线 \(r\) 和直线 \(s\) 的交点。（尚未证明 \(D\) 在圆上。）

　　 由构造得知，四边形 \(ABCD\) 是一个平行四边形（因为对边平行）。由于在平行四边形中，邻角互为补角（加起来等于 180°），而 \(\angle ABC\) 是直角（90°），因此角 \(\angle BAD\)、\(\angle BCD\)、\(\angle ADC\) 也都是直角（90°）；因此，\(ABCD\) 是一个矩形。

　　 设 \(O\) 为对角线 \(\overline{AC}\) 和 \(\overline{BD}\) 的交点。根据上述第二个事实，点 \(O\) 与 \(A\)、\(B\) 和 \(C\) 的距离相等。因此，\(O\) 是外接圆的圆心，且三角形的斜边（\(\overline{AC}\)）是该圆的直径。

使用几何学的逆命题替代证明

　　 给定一个直角三角形 \(ABC\)，其中是斜边，构造一个以 \(AC\) 为直径的圆 \(\Omega\)。设 \(O\) 为Ω的圆心。设 \(D\) 为 \(\Omega\) 与射线 \(OB\) 的交点。根据塔勒斯定理，\(\angle ADC\) 是直角。但此时 \(D\) 必须等于 \(B\)。（如果 \(D\) 位于 \(\triangle ABC\) 内部，\(\angle ADC\) 将是钝角；如果 \(D\) 位于 \(\triangle ABC\) 外部，\(\angle ADC\) 将是锐角。）

使用线性代数证明逆命题

　　 此证明利用了两个事实：

1. 两条直线若形成直角，则它们的方向向量的点积为零；
2. 向量的长度的平方由该向量与自身的点积给出。

　　 设 \(\angle ABC\) 为直角，\(M\) 为以 \(\overline{AC}\) 为直径的圆。为了简化计算，设 \(M\) 的圆心位于原点。那么我们知道：

• \(A = -C\)，因为以原点为圆心的圆的直径是 \(\overline{AC}\)，并且
• \((A - B) \cdot (B - C) = 0\)，因为 \(\angle ABC\) 是直角。

　　 由此得出： \[ 0 = (A - B) \cdot (B - C)~ \] \[ = (A - B) \cdot (B + C)~ \] \[ = |A|^2 - |B|^2.~ \] \[ \therefore |A| = |B|.~ \] 这意味着 \(A\) 和 \(B\) 到原点的距离相等，即它们到 \(M\) 的圆心的距离相等。由于 \(A\) 在 \(M\) 上，\( B\) 也在 \(M\) 上，因此圆 M 是三角形的外接圆。

　　 上述计算实际上证明了塔勒斯定理的两个方向在任何内积空间中都成立。

4. 推广和相关结果

　　 如上所述，塔勒斯定理是内切角定理的一个特例（其证明与上述给出的塔勒斯定理的第一个证明非常相似）：

　　 给定圆心为 \(O\) 的圆上的三点 \(A\)、\(B\) 和 \(C\)，角 \(\angle AOC\) 是角 \(\angle ABC\) 的两倍。

　　 与塔勒斯定理相关的结果如下：

　　 如果 AC 是圆的直径，则：

• 如果 \(B\) 在圆内，则 \(\angle ABC>90^\circ\)；
• 如果 \(B\) 在圆上，则 \(\angle ABC=90^\circ\)；
• 如果 \(B\) 在圆外，则 \(\angle ABC<90^\circ\)。

5. 应用

构造通过一点的圆的切线

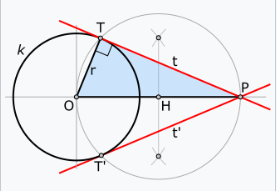
　　 塔勒斯定理可以用来构造通过给定点的圆的切线。在右图中，给定圆 \(K\) 的圆心为 \(O\)，点 \(P\) 在圆外，先在 \(\overline{OP}\) 上找到中点 \(H\)，然后以 \(H\) 为圆心，\(\overline{OH}\) 为半径绘制一个圆。\(\overline{OP}\) 是该圆的直径，因此连接 \(\overline{OP}\) 与圆与点 \(T\) 和 \(T'\) 的交点的三角形都是直角三角形。

找到圆的圆心

　　 塔勒斯定理还可以用来通过一个具有直角的物体（如三角尺或比圆大且矩形的纸张）找到圆的圆心。[7] 角度被放置在圆的任意一个圆周上（图 1）。两条边与圆周的交点定义了一个直径（图 2）。重复这个过程，使用另一组交点得到另一个直径（图 3）。圆心位于这两个直径的交点处。

6. 另见

• 合成几何
• 逆毕达哥拉斯定理

7. 注释

1. Heath, Thomas L. (1956). *The Thirteen Books of Euclid's Elements*. 第 2 卷（第 3–9 卷）（第 2 版）。Dover，第 61 页。ISBN 0486600890。最初由剑桥大学出版社出版，第一版 1908 年，第二版 1926 年。
2. de Laet, Siegfried J. (1996). *History of Humanity: Scientific and Cultural Development*. 联合国教科文组织，第 3 卷，第 14 页。ISBN 92-3-102812-X
3. Dicks, D. R. (1959). "Thales". *The Classical Quarterly*. 9 (2): 294–309. doi:10.1017/S0009838800041586.
4. Allen, G. Donald (2000). "Thales of Miletus" (PDF)。检索于 2012-02-12。
5. Patronis, Tasos; Patsopoulos, Dimitris (2006 年 1 月). "The Theorem of Thales: A Study of the Naming of Theorems in School Geometry Textbooks". *The International Journal for the History of Mathematics Education*: 57–68. ISSN 1932-8826。2013-11-05 归档。
6. Sidoli, Nathan (2018). "Greek mathematics" (PDF)。在 Jones, A.; Taub, L.（主编）。*The Cambridge History of Science: Vol. 1, Ancient Science*。剑桥大学出版社，第 345–373 页。
7. *Resources for Teaching Mathematics*: 14–16 Colin Foster

8. 参考文献

• Agricola, Ilka; Friedrich, Thomas (2008). *Elementary Geometry*. AMS，第 50 页。ISBN 978-0-8218-4347-5.
• Heath, T.L. (1921). *A History of Greek Mathematics: From Thales to Euclid*. 第 1 卷。牛津，第 131 页及以下。

9. 外部链接

• Weisstein, Eric W. "Thales' Theorem". *MathWorld*.
• *Munching on Inscribed Angles*
• 塔勒斯定理解释，带有互动动画
• 由 Michael Schreiber 提供的塔勒斯定理演示，*Wolfram Demonstrations Project*