首都师范大学 2010 年硕士考试试题

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 半圆型光滑凹槽竖直固定在水平地面上，一质量为 m 的质点从凹槽的任一端最高处由静止开始无摩擦地滑下。求:在质点运动过程中,凹槽给与质点的支撑力的变化情况。
2. 将一轻质弹簧放在两个木块之间，并与它们固定连接，构成一个系统。木块的质量分别为 m 和 M，放在光滑水平面上。初始，系统静止，弹簧处于自然状态。后给予质量为 m 的木块一冲量，使其获得沿弹簧压缩方向的水平速率 $v_0$。在系统的质心系中试求:
   (1)两木块各做何种运动？
   (2)当弹簧处于原长状态时，系统的总能量在两个木块之间是如何分配的？
3. 一根长度为 L、质量为 M 的均匀细直杆，其一端悬挂在一光滑、水平轴上，杆可以绕轴在竖直面内做自由摆动。另一完全同样的杆与其并排悬挂(两水平轴平行)。初始两杆静止，且刚刚可以接触。后，将其中的一杆(令其为杆 1)拉起一定角度 $\theta_0$ 后放手，使两杆发生完全弹性碰撞，求:
   (1)碰撞后，被碰撞杆(即杆 2)摆起的角度 $\theta$;
   (2)两杆发生两次碰撞的时间间隔。
4. 已知地球表面的重力加速度为 $9.8ms^{-2}$，围绕地球的大圆周长为 $4*10^7$m，月球与地球的直径及质量之比分别是 $\frac{D_m}{D_e}$=0.27 和 $\frac{M_m}{M_e}$=0.0123。试计算从月球表面逃离月球引力场所必需的最小速度。
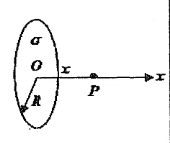
5. 半径为 R 的圆平面上，分布着电荷面密度为σ的均匀正电荷，过圆平面的中心，做垂直于平面的 ox 轴，P 点在轴线上，与原点相距为 x 处，如图。求:
   (1)该带电圆平面在 P 点处产生的电场强度 $\vec E_p$;
   (2)若 P 点沿 x 轴远移，当移到足够远时，该带电圆平面可以被看做点电荷模型，证明 $\vec E_p$ 在 $x \to \infty$ 时可表示成点电荷的电场表达式。
   提示 $\displaystyle \frac{1}{\sqrt{1+x}}=(1-\frac{1}{2}x+\frac{1*3}{2*4}x^2-\frac{1*3*5}{2*4*6}x^3+\dots)$ 其中 x 是小量。
   
   图 1
6. 已知氢原子模型的基础数据为:基态电子的轨道半径为 $a=0.53*10^{-8}cm$;电子匀速圆周运动的速率为 $v=2.2*10^8cm/s$;电子电荷为 $e=1.6*10^{-19}C$。试求:
   (1)电子圆运动在其轨道中心产生的磁感应强度 B 的大小;
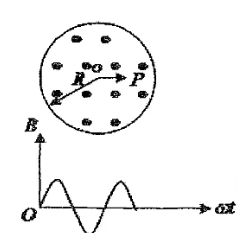
   (2)电子圆运动的轨道磁矩 $P_m$ 的大小。
7. 半径为 R 的圆形区域内，均匀分布着强度为 $\vec B=\vec B_0 \sin \omega t$ 的磁场，方向如图。求:
   (1)该磁场中，距离圆形区域中心点 o 为 r 的 P 点处的涡旋电场强度 $\vec E_\text{涡}$;
   (2)该点处电磁场的能流密度 $\vec S$;
   (3)画出 P 点磁感应强度变化一个周期对应的能流随时间变化的周期图像。
   
   图 2
8. 两半径为 R 的圆形金属板构成平行板电容器，加在该电容器上的交变电场为 $E(t)=E_0 \cos \omega t$，设电荷在电容器极板上均匀分布，且边缘效应可忽略。试求:
   (1)电容器中的位移电流密度表达式;
   (2)若 $E_0=720v/m,\omega=10^5\pi$,求经过 $t=2.0*10^{-5}S$,距电容器极板中心连线为 r=1.0cm(r<R)处的磁感应强度的大小。