斯涅尔定律（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 斯涅尔定律（也称为斯涅尔-笛卡尔定律、伊本·萨尔定律[^1]，或折射定律）是一种描述入射角和折射角之间关系的公式，适用于光或其他波在两种不同各向同性介质（如水、玻璃或空气）的边界处传播时的情况。在光学中，该定律用于光线追踪以计算入射角或折射角，也用于实验光学中测定材料的折射率。该定律在具有负折射率的超材料中同样适用，这些材料允许光以 “向后” 折射的方式弯曲，形成负折射角。

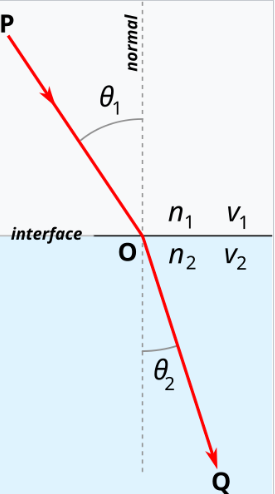
　　 定律指出，对于一对给定的介质，入射角（\( \theta_1 \)）的正弦与折射角（\( \theta_2 \)）的正弦之比，等于第二介质相对于第一介质的折射率（\( n_{21} \)），也等于两介质的折射率之比（\( \frac{n_2}{n_1} \)），或者等价于两介质中相位速度之比（\( \frac{v_1}{v_2} \)）[^2]。 \[ \frac{\sin \theta_1}{\sin \theta_2} = n_{21} = \frac{n_2}{n_1} = \frac{v_1}{v_2}~ \] 斯涅尔定律可以从费马最短时间原理推导而来，而费马原理本身是基于光作为波传播的特性得出的。

1. 历史

　　 托勒密在埃及亚历山大的研究中发现了关于折射角的某种关系，但对于较大的角度来说，这一关系并不准确。托勒密确信自己找到了一个精确的经验定律，这部分是因为他对数据进行了轻微的修改以符合理论（参见：确认偏误）。

　　 这一定律最终以斯涅尔命名，尽管最早发现这一规律的是波斯科学家伊本·萨赫尔（Ibn Sahl）。984 年，萨赫尔在巴格达宫廷中撰写的《关于燃烧镜与透镜》手稿中，运用该定律推导出了能够无几何像差聚焦光线的透镜形状。

　　 海什木（Alhazen）在其 1021 年完成的《光学书》中几乎重新发现了折射定律，但他未能迈出最后一步。

　　 1602 年，托马斯·哈里奥特（Thomas Harriot）重新发现了这一定律，但他并未发表其成果，尽管他曾与开普勒就这一主题进行过通信。1621 年，荷兰天文学家威利布罗德·斯涅利乌斯（Willebrord Snellius，1580–1626，即斯涅尔）推导出一种数学上等效的表达形式，但在他生前并未出版。1637 年，勒内·笛卡尔（René Descartes）通过一种基于正弦的启发性动量守恒论证，独立推导出了该定律，并在他的文章《光学》中运用该定律解决了许多光学问题。

　　 皮埃尔·费马（Pierre de Fermat）拒绝接受笛卡尔的解法，而是基于他的最短时间原理，独立得出了同样的结论。笛卡尔假设光速是无限的，但在其推导中又假设介质越密，光速越快。费马则持相反假设，即光速是有限的，而且光速在密度较高的介质中较慢。他的推导依赖于这一假设。此外，费马的推导还使用了他发明的 “等适性”（adequality），这一数学方法相当于微积分，用于求解极值和切线问题。

　　 在笛卡尔的影响力著作《几何学》中，他解决了由帕加的阿波罗尼乌斯和亚历山大的帕普斯研究过的一个问题。已知 \( n \) 条直线 \( L \) 和每条直线上的一点 \( P(L) \)，寻找满足某些条件的点 \( Q \) 的轨迹。例如，当 \( n = 4 \) 时，已知直线 \( a \)、\( b \)、\( c \) 和 \( d \)，以及分别位于这些直线上的点 \( A \)、\( B \)、\( C \) 和 \( D \)，寻找点 \( Q \) 的轨迹，使得线段 \( QA \) 和 \( QB \) 的乘积等于 \( QC \) 和 \( QD \) 的乘积。当这些直线不全平行时，帕普斯证明了轨迹是圆锥曲线；但当笛卡尔研究更大的 \( n \) 时，他得出了三次和更高次的曲线。为了证明这些三次曲线的趣味性，他展示了它们自然地从斯涅尔定律在光学中产生。[16]

　　 根据戴克斯特赫伊斯的说法，[17]“在《光的性质与特性》（1662）中，艾萨克·沃修斯声称笛卡尔曾见过斯涅尔的论文并炮制了自己的证明。我们现在知道这个指控是无根据的，但它后来被多次引用。” 费马和惠更斯也重复了这一指控，称笛卡尔抄袭了斯涅尔。在法语中，斯涅尔定律有时被称为 “笛卡尔定律”（la loi de Descartes）或更常见的 “斯涅尔-笛卡尔定律”（loi de Snell-Descartes）。

　　 在 1678 年的《光论》中，克里斯蒂安·惠更斯（Christiaan Huygens）展示了如何通过光的波动性，利用我们现在称为惠更斯-菲涅耳原理（Huygens–Fresnel principle），解释或推导出斯涅尔的正弦定律。

　　 随着现代光学和电磁理论的发展，古老的斯涅尔定律进入了新的阶段。1962 年，尼古拉斯·布隆伯根（Nicolaas Bloembergen）证明，在非线性介质的边界上，斯涅尔定律应被写成一般形式。[18] 2008 年和 2011 年，研究还表明，等离子体超表面可以改变光束的反射和折射方向。[19][20]

2. 解释

　　 斯涅尔定律用于确定光线通过具有不同折射率的介质时的传播方向。介质的折射率（标记为 \(n_1\)、\(n_2\) 等）表示光线在折射介质（如玻璃或水）中传播时，其速度相对于在真空中传播速度的减小倍数。

　　 当光穿过介质边界时，根据两个介质的相对折射率，光线将以较小或较大的角度发生折射。这些角度是相对于边界的法线（垂直于边界的线）来测量的。例如，当光从空气进入水中时，由于光在水中的传播速度变慢，它会朝向法线方向折射；相反，当光从水进入空气时，它会远离法线方向折射。

　　 在两个表面之间的折射被认为是可逆的，因为如果所有条件完全相同，那么光在相反方向传播时的角度也会相同。

　　 斯涅尔定律通常仅适用于各向同性或镜面介质（如玻璃）。对于某些晶体等各向异性介质，由于双折射现象，折射光线可能分裂为两束光线：一束是遵循斯涅尔定律的普通光（o 光线），另一束是可能与入射光线不共面的特殊光（e 光线）。

　　 当所涉及的光或波是单色波（即单一频率）时，斯涅尔定律还可以用两个介质中波长的比值来表示，即 \(\lambda_1\) 和 \(\lambda_2\)： \[ \frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2} = \frac{\lambda_1}{\lambda_2}~ \] 其中，\(\sin \theta_1\) 和 \(\sin \theta_2\) 分别是入射角和折射角的正弦值，\(\lambda_1\) 和 \(\lambda_2\) 分别是两个介质中的波长。

3. 推导与公式

　　 斯涅尔定律可以通过多种方式推导出来。

从费马原理的推导

　　 斯涅尔定律可以从费马原理推导出来，该原理指出光线会沿着用时最短的路径传播。通过对光学路径长度求导，可以找到光线传播的平稳点，从而确定光线所走的路径。（在某些情况下，例如光在一个（球面）镜上反射时，光线可能会违反费马原理，而不沿用时最短的路径传播。）在一个经典的类比中，低折射率的区域被比作沙滩，高折射率的区域被比作海洋，救援人员从沙滩跑向海里溺水者的最快路径遵循斯涅尔定律。

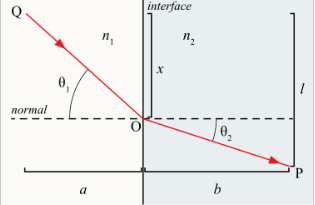
　　 如图 6 所示，假设介质 1 和介质 2 的折射率分别为 \( n_1 \) 和 \( n_2 \)。光线通过点 O 从介质 1 进入介质 2。

　　 \( \theta_1 \) 是入射角，与法线的夹角。\( \theta_2 \) 是折射角，与法线的夹角。

　　 光在介质 1 和介质 2 中的相速度分别为： \[ v_1 =c/n_1, \quad v_2 = c/n_2~ \] 其中，\( c \) 是真空中的光速。

　　 令 \( T \) 表示光线从点 \( Q \) 经点 \( O \) 到点 \( P \) 所需的时间。 \[ T = \frac{\sqrt{x^2 + a^2}}{v_1} + \frac{\sqrt{b^2 + (l - x)^2}}{v_2} = \frac{\sqrt{x^2 + a^2}}{v_1} + \frac{\sqrt{b^2 + l^2 - 2lx + x^2}}{v_2}~ \] 其中，\( a \)、\( b \)、\( l \) 和 \( x \) 如上图 6 所示，\( x \) 为变化参数。

　　 为了最小化 \( T \)，可以对其求导： \[ \frac{dT}{dx} = \frac{x}{v_1 \sqrt{x^2 + a^2}} - \frac{(l - x)}{v_2 \sqrt{(l - x)^2 + b^2}} = 0 \quad \text{(极值点)}~ \] 注意到： \[ \frac{x}{\sqrt{x^2 + a^2}} = \sin \theta_1~ \] 和 \[ \frac{l - x}{\sqrt{(l - x)^2 + b^2}} = \sin \theta_2~ \] 因此： \[ \frac{dT}{dx} = \frac{\sin \theta_1}{v_1} - \frac{\sin \theta_2}{v_2} = 0~ \] 即： \[ \frac{\sin \theta_1}{v_1} = \frac{\sin \theta_2}{v_2}~ \] 代入相速度公式： \[ \frac{n_1 \sin \theta_1}{c} = \frac{n_2 \sin \theta_2}{c}~ \] 化简后得到斯涅尔定律： \[ n_1 \sin \theta_1 = n_2 \sin \theta_2~ \]

从惠更斯原理的推导

　　 另一种方法是通过分析从光源到观察者的所有可能路径的光波干涉推导出斯涅尔定律——最终会因为路径间的干涉导致相长或相消。

4. 从麦克斯韦方程组的推导

　　 斯涅尔定律还可以通过应用麦克斯韦方程组中描述电磁辐射与感应的一般边界条件来推导。

从能量和动量守恒的推导

　　 斯涅尔定律的另一个推导方法基于平移对称性的考虑。[21] 例如，与 \( z \) 方向垂直的均匀表面不会改变横向动量。由于传播矢量 \(\vec{k}\) 与光子的动量成正比，横向传播方向 \((k_x, k_y, 0)\) 在两个区域中必须保持不变。

　　 假设不失一般性，将入射面置于 \( z, x \) 平面中：\(k_{x\text{Region}_1} = k_{x\text{Region}_2}.\) 利用波数与介质折射率之间的已知关系，可以立即推导出斯涅尔定律： \[ k_{x\text{Region}_1} = k_{x\text{Region}_2}~ \] \[ n_1 k_0 \sin \theta_1 = n_2 k_0 \sin \theta_2~ \] \[ n_1 \sin \theta_1 = n_2 \sin \theta_2~ \] 其中 \( k_0 = \frac{2\pi}{\lambda_0} = \frac{\omega}{c} \) 是真空中的波数。

　　 尽管在原子尺度上没有表面是真正均匀的，但只要区域在光的波长尺度上是均匀的，完全的平移对称性就是一个非常好的近似。

向量形式

　　 给定一个归一化的光矢量 \( \vec{l} \)（指向从光源到表面的方向）和一个归一化的法线矢量 \( \vec{n} \)，可以通过入射角 \( \theta_1 \) 和折射角 \( \theta_2 \) 的余弦值，推导出归一化的反射和折射光线，而无需显式使用正弦值或任何三角函数或角度：[22] \[ \cos \theta_1 = -\vec{n} \cdot \vec{l}~ \] \(\cos \theta_1\) 必须为正，这会发生在 \( \vec{n} \) 是指向光源一侧的法线时，该侧的折射率为 \( n_1 \)。如果 \(\cos \theta_1\) 为负，则说明 \( \vec{n} \) 指向无光的一侧，因此应重新开始，并将 \( \vec{n} \) 替换为其负值。 \[ \vec{v}_{\mathrm{reflect}} = \vec{l} + 2\cos \theta_1 \vec{n}~ \] 该反射方向矢量指向光线到达表面的那一侧。

　　 现在应用斯涅尔定律，通过正弦比推导出折射光方向矢量的公式： \[ \sin \theta_2 = \left( \frac{n_1}{n_2} \right) \sin \theta_1 = \left( \frac{n_1}{n_2} \right) \sqrt{1 - \left( \cos \theta_1 \right)^2}~ \] \[ \cos \theta_2 = \sqrt{1 - (\sin \theta_2)^2} = \sqrt{1 - \left( \frac{n_1}{n_2} \right)^2 \left( 1 - \left( \cos \theta_1 \right)^2 \right)}~ \] \[ \vec{v}_{\text{refract}} = \left( \frac{n_1}{n_2} \right) \vec{l} + \left( \frac{n_1}{n_2} \cos \theta_1 - \cos \theta_2 \right) \vec{n}~ \]

　　 该公式可以通过重新命名简单变量来简化，定义为： \( r = n_1 / n_2 \) 和 \( c = -\vec{n} \cdot \vec{l} \)，从而避免使用三角函数名称或角度名称： \[ \vec{v}_{\text{refract}} = r\vec{l} + \left( rc - \sqrt{1 - r^2 (1 - c^2)} \right)\vec{n}~ \] 示例： 已知： \[ \vec{l} = \{0.707107, -0.707107\},~\vec{n} = \{0, 1\},~r = \frac{n_1}{n_2} = 0.9~ \]

　　 计算： \[ c = \cos \theta_1 = 0.707107, \quad \cos \theta_2 = \sqrt{1 - r^2 (1 - c^2)} = 0.771362~ \] \[ \vec{v}_{\text{reflect}} = \{0.707107, 0.707107\}~ \] \[ \vec{v}_{\text{refract}} = \{0.636396, -0.771362\}~ \] 余弦值可以保存下来，并在菲涅耳方程中用于计算反射光和折射光的强度。

　　 当计算 \(\cos \theta_2\) 的方程中出现负的根号下值时，表明发生了全反射，这只能在光线从光密介质（\(n_1\)）进入光疏介质（\(n_2 < n_1\)）时才会发生。

5. 全内反射与临界角

　　 当光从折射率较高的介质传播到折射率较低的介质时，斯涅尔定律在某些情况下（每当入射角足够大时）似乎要求折射角的正弦值大于 1。这显然是不可能的，因此在这种情况下，光会被边界完全反射，这种现象称为全内反射。仍然能产生折射光线的最大入射角称为临界角；在这种情况下，折射光线沿着两个介质的边界传播。

　　 例如，考虑一束光从水中射向空气，入射角为 50°。水和空气的折射率分别约为 1.333 和 1，因此斯涅尔定律给出了以下关系： \[ \sin \theta_2 = \frac{n_1}{n_2} \sin \theta_1 = \frac{1.333}{1} \cdot \sin\left(50^\circ\right) = 1.333 \cdot 0.766 = 1.021~ \] 这是不可能满足的。临界角 \(\theta_{\text{crit}}\) 是使得折射角 \(\theta_2\) 等于 90°时的入射角 \(\theta_1\) 的值： \[ \theta_{\text{crit}} = \arcsin \left( \frac{n_2}{n_1} \right) = \arcsin \left( \frac{1}{1.333} \right) = 48.6^\circ~ \]

6. 色散

　　 在许多波传播介质中，波速随着波的频率或波长的变化而变化；这一现象在大多数透明物质中传播光时也存在，除了真空之外。这些介质被称为色散介质。结果是，斯涅尔定律所决定的折射角也会依赖于频率或波长，因此混合波长的光线，如白光，会发生扩散或色散。这种光在玻璃或水中的色散现象是彩虹和其他光学现象的来源，在这些现象中，不同波长的光表现为不同的颜色。

　　 在光学仪器中，色散会导致色差；即与颜色相关的模糊，这有时会限制分辨率。这在折射望远镜中尤其明显，在消色差物镜发明之前尤其如此。

7. 有损、吸收或导电介质

　　 在导电介质中，介电常数和折射率是复值的。因此，折射角和波矢也都是复值的。这意味着，尽管常实相位的表面是平面，其法线与界面法线之间的夹角等于折射角，但常振幅的表面则是与界面平行的平面。由于这两平面通常不重合，波被认为是非均匀的。折射波会指数衰减，其衰减指数与折射率的虚部成正比。

8. 另见

• 最速降线曲线 – 雅各布·伯努利的简单证明，描述没有摩擦的最快下坡曲线
• 变分学 – 函数空间上的微分学
• 大气中无线电波衰减的计算
• 渐逝波 – 一种场，其中电磁能量的净流动为零
• 哈密顿光学
• 折射率列表
• N 缝干涉方程
• 反射（物理学）– 波在界面上的 “反弹”
• 斯涅尔窗口 – 由于斯涅尔定律引起的水下现象
• 光的折射率与波长 – 折射率与波长之间的经验关系

9. 参考文献

1. Boudrioua, Azzedine; Rashed, Roshdi; Lakshminarayanan, Vasudevan (2017-08-15). *Light-Based Science: Technology and Sustainable Development, The Legacy of Ibn al-Haytham*. CRC Press. p. 207. ISBN 978-1-351-65112-7. *Yao, X. Steve; Chen, Xiaojun (James) (2022). *Polarization Measurement and Control in Optical Fiber Communication and Sensor Systems*. John Wiley & Sons. p. 4. ISBN 978-1-119-75850-1. *Wolf, K B; Krotzsch, G (1995-01-01). "Geometry and dynamics in refracting systems". *European Journal of Physics*. 16 (1): 14–20. Bibcode:1995EJPh...16...14W. doi:10.1088/0143-0807/16/1/003. ISSN 0143-0807. *Wolf, Kurt Bernardo (2004-07-21). *Geometric Optics on Phase Space*. Springer Science & Business Media. ISBN 978-3-540-22039-8.
2. Born 和 Wolf (1959). *Principles of Optics*. 纽约，NY：Pergamon Press INC. p. 37.
3. David Michael Harland (2007). "Cassini at Saturn: Huygens results". p.1. ISBN 0-387-26129-X
4. "Ptolemy (约公元 100 年-约公元 170 年)". Eric Weinstein's *World of Scientific Biography*.
5. William Whewell, *History of the Inductive Science from the Earliest to the Present Times*, 伦敦：John H. Parker，1837 年。
6. Papadopoulos, Athanase (2017). "Roshdi Rashed, Greek 和 Arabic 数学史学家". *HAL Open Science*. p. 12. hal-01653436.
7. Mourad Zghal; Hamid-Eddine Bouali; Zohra Ben Lakhdar; Habib Hamam. "学习光学的第一步：Ibn Sahl、Al-Haytham 和 Young 关于折射的研究作为典型例子" (PDF). R. Rashed 将折射定律的发现归功于 Ibn Sahl，通常称为斯涅尔定律，也被称为斯涅尔和笛卡尔定律。 参考文献
8. Smith, A. Mark (2015). *From Sight to Light: The Passage from Ancient to Modern Optics*. 芝加哥大学出版社。p. 178. ISBN 978-0-226-17476-1.
9. Rashed, Roshdi (1990). "A pioneer in anaclastics: Ibn Sahl on burning mirrors and lenses". *Isis*. 81 (3): 464–491. doi:10.1086/355456. S2CID 144361526. [争议 – 讨论][需要澄清]
10. A. I. Sabra (1981). *Theories of Light from Descartes to Newton*, 剑桥大学出版社。(参见 Pavlos Mihas, *Use of History in Developing ideas of refraction, lenses and rainbow*, p. 5, Demokritus University, Thrace, Greece.)
11. Kwan, A.; Dudley, J.; Lantz, E. (2002). "Who really discovered Snell's law?". *Physics World*. 15 (4): 64. doi:10.1088/2058-7058/15/4/44.
12. Florian Cajori, *A History of Physics in its Elementary Branches: Including the Evolution of Physical Laboratories* (1922)
13. Ferdinand Rosenberger, *Geschichte der Physik* (1882) 第二部分，p. 114
14. Carl Benjamin Boyer, *The Rainbow: From Myth to Mathematics* (1959)
15. Florian Cajori, "Who was the First Inventor of Calculus" *The American Mathematical Monthly (1919) Vol.26
16. The Geometry of Rene Descartes(Dover Books on Mathematics) by Rene Descartes, David Eugene Smith and Marcia L. Latham (1954 年 6 月 1 日)
17. Dijksterhuis, Fokko Jan (2004). *Lenses and Waves: Christiaan Huygens and the Mathematical Science of Optics in the Seventeenth Century*. Springer. ISBN 1-4020-2697-8.
18. Bloembergen, N.; Pershan, P. S. (1962). "Light waves at the boundary of nonlinear media" (PDF). *Physical Review*. 128 (2): 606. Bibcode:1962PhRv..128..606B. doi:10.1103/PhysRev.128.606. hdl:1874/7432. Archived (PDF) from the original on 2022-10-09.
19. Xu, T.; et al. (2008). "Plasmonic deflector". *Opt. Express*. 16 (7): 4753–9. Bibcode:2008OExpr..16.4753X. doi:10.1364/oe.16.004753. PMID 18542573.
20. Yu, Nanfang; Genevet, Patrice; Kats, Mikhail A.; Aieta, Francesco; Tetienne, Jean-Philippe; Capasso, Federico; Gaburro, Zeno (2011 年 10 月). "Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction". *Science*. 334 (6054): 333–7. Bibcode:2011Sci...334..333Y. doi:10.1126/science.1210713. PMID 21885733. S2CID 10156200.
21. Joannopoulos, John D; Johnson, SG; Winn, JN; Meade, RD (2008). *Photonic Crystals: Molding the Flow of Light* (第二版). 普林斯顿，NJ：普林斯顿大学出版社。p. 31. ISBN 978-0-691-12456-8.
22. Glassner, Andrew S. (1989). *An Introduction to Ray Tracing*. Morgan Kaufmann. ISBN 0-12-286160-4.
23. Born 和 Wolf，第 13.2 节，"金属表面的折射与反射"
24. Hecht, *Optics*, 第 4.8 节，金属的光学性质。
25. S. J. Orfanidis, *Electromagnetic Waves & Antennas*, 第 7.9 节，"斜入射到有损介质"，[1] 于 2020 年 7 月 30 日通过 Wayback Machine 存档

10. 外部链接

• Ibn Sahl 和斯涅尔定律 [2016-10-23 于 Wayback Machine 存档]
• 折射定律的发现
• Todd Rowland 的 *Snell's Law of Refraction (Wave Fronts)*，Wolfram Demonstrations Project
• 莱顿市中心墙上的斯涅尔定律 [2018-04-27 于 Wayback Machine 存档]
• 海岸线效应