热力学（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

1. 热力学

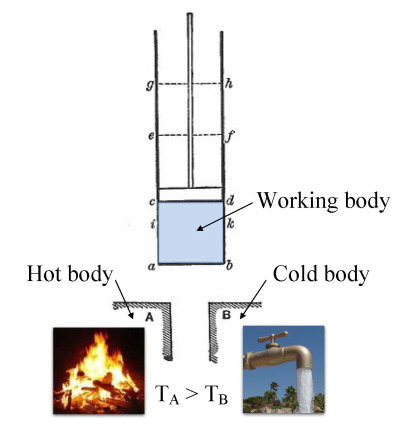
　　 热力学研究热量、功和温度，以及它们与能量、熵以及物质和辐射的物理性质之间的关系。这些量的行为由热力学四大定律所支配，这些定律通过可测量的宏观物理量进行定量描述，但可以通过统计力学从微观成分的角度加以解释。热力学在科学和工程的广泛领域中起着重要作用。

　　 从历史上看，热力学起源于提高早期蒸汽机效率的需求，尤其是在法国物理学家萨迪·卡诺（1824 年）的工作下，他认为发动机的效率是帮助法国赢得拿破仑战争的关键。[1] 苏格兰-爱尔兰物理学家开尔文勋爵是第一个在 1854 年给出简明定义的人，[2] 他说：“热力学是研究热量与作用于物体接触部分之间的力以及热量与电作用之间关系的学科。” 德国物理学家和数学家鲁道夫·克劳修斯重新阐述了卡诺循环，并为热理论提供了更真实、更可靠的基础。他于 1850 年发表的论文《论热的动因》[3] 首次提出了热力学第二定律。1865 年，他引入了熵的概念。1870 年，他引入了适用于热的维里定理。[4]

　　 热力学的最初应用于机械热机，随后迅速扩展到化合物和化学反应的研究。化学热力学研究熵在化学反应过程中的作用本质，为该领域的扩展和知识提供了大部分内容。其他形式的热力学也随之出现。统计热力学或统计力学关注从微观行为出发对粒子集体运动的统计预测。1909 年，康斯坦丁·卡拉西奥多里提出了一种纯数学方法的公理化表述，这种描述通常被称为几何热力学。

2. 引言

　　 任何热力学系统的描述都运用热力学四大定律，这些定律构成了公理基础。第一定律规定能量可以通过热、功以及物质转移在物理系统之间传递。[5] 第二定律定义了熵这一量的存在，它描述了系统在热力学上可以演变的方向，量化了系统的有序状态，并可用于量化系统中可提取的有用功。[6]

　　 在热力学中，研究并分类大量物体之间的相互作用。热力学系统及其环境的概念在这里是核心。一个系统由粒子组成，这些粒子的平均运动定义了系统的性质，而这些性质则通过状态方程相互关联。属性可以组合以表达内能和热力学势，这对于确定平衡条件和自发过程非常有用。

　　 通过这些工具，热力学可以用来描述系统如何响应环境的变化。这可以应用于科学和工程的许多领域，如发动机、相变、化学反应、传输现象，甚至黑洞。热力学的结果对于物理学的其他领域以及化学、化学工程、腐蚀工程、航空航天工程、机械工程、细胞生物学、生物医学工程、材料科学和经济学等都至关重要。[7][8]

　　 本文主要集中在经典热力学，经典热力学主要研究热力学平衡态的系统。非平衡热力学通常被视为经典处理的扩展，但统计力学为这一领域带来了许多进展。

3. 历史

图
图 1：热力学的最初八大学派的热力学家。对现代热力学版本影响最深远的学派是柏林学派，特别是鲁道夫·克劳修斯（Rudolf Clausius）1865 年出版的《热的机械理论》一书，维也纳学派，卢德维希·玻尔兹曼（Ludwig Boltzmann）的统计力学，以及耶鲁大学的吉布斯学派，威拉德·吉布斯（Willard Gibbs）1876 年的著作《异质物质的平衡》及其引发的化学热力学研究。[9]

　　 热力学作为一门科学学科的历史通常始于奥托·冯·盖里克（Otto von Guericke），他在 1650 年制造并设计了世界上第一台真空泵，并通过他的马格德堡半球演示了真空。盖里克之所以制作真空，是为了反驳亚里士多德长期以来认为 “自然厌恶真空” 的假设。紧接着，英爱物理学家和化学家罗伯特·波义耳（Robert Boyle）得知了盖里克的设计，并在 1656 年与英国科学家罗伯特·胡克（Robert Hooke）合作，制造了一台空气泵。[10] 使用这台泵，波义耳和胡克注意到压力、温度和体积之间的关联。随着时间的推移，波义耳定律得以提出，表明压力和体积成反比。然后，在 1679 年，基于这些概念，波义耳的同事丹尼斯·帕平（Denis Papin）制造了一台蒸汽消化器，这是一种密封容器，带有紧密的盖子，能够将蒸汽困在其中，直到产生高压。

　　 后来，设计中加入了一个蒸汽释放阀，以防止机器爆炸。通过观察阀门有节奏地上下运动，帕平构思出了活塞和气缸发动机的想法。然而，他并未继续进行这一设计。尽管如此，在 1697 年，基于帕平的设计，工程师托马斯·萨弗里（Thomas Savery）制造了第一台发动机，随后托马斯·纽科门（Thomas Newcomen）于 1712 年进行了改进。尽管这些早期的发动机粗糙且低效，但它们引起了当时领先科学家的关注。

　　 热容和潜热这两个热力学发展的基础概念，是由格拉斯哥大学的约瑟夫·布莱克（Joseph Black）教授提出的，詹姆斯·瓦特（James Watt）曾在该校担任仪器制造师。布莱克和瓦特一起进行实验，但正是瓦特构思了外部冷凝器的想法，这一设计大大提高了蒸汽机的效率。[11] 基于前人的工作，萨迪·卡诺（Sadi Carnot），被誉为 “热力学之父”，于 1824 年出版了《火的动力反思》（Reflections on the Motive Power of Fire），这本书探讨了热、动力、能量和发动机效率。书中概述了卡诺发动机、卡诺循环与动力之间的基本能量关系，标志着热力学作为一门现代科学的开端。[12]

　　 第一本热力学教科书由威廉·兰金（William Rankine）于 1859 年编写，他最初受过物理学训练，并曾在格拉斯哥大学担任土木与机械工程教授。[13] 热力学的第一定律和第二定律在 1850 年代同时提出，主要来自威廉·兰金、鲁道夫·克劳修斯和威廉·汤姆森（凯尔文勋爵）的研究工作。统计热力学的基础是由詹姆斯·克拉克·麦克斯韦、卢德维希·玻尔兹曼、马克斯·普朗克、鲁道夫·克劳修斯和 J·威拉德·吉布斯等物理学家奠定的。

　　 克劳修斯在 1850 年发表的论文《论热的动力》中首次阐述了第二定律的基本思想，[3] 他被称为 “热力学的奠基人之一”，[14] 并于 1865 年提出了熵的概念。

　　 在 1873 至 1876 年间，美国数学物理学家乔赛亚·威拉德·吉布斯（Josiah Willard Gibbs）发表了三篇重要论文，其中最著名的是《异质物质的平衡》，[15] 在这篇论文中，他展示了如何通过研究热力学系统的能量、熵、体积、温度和压力来图解热力学过程，包括化学反应，从而判断某一过程是否会自发发生。[16] 此外，皮埃尔·杜厄（Pierre Duhem）在 19 世纪也撰写了关于化学热力学的著作。[17] 在 20 世纪初，化学家如吉尔伯特·N·刘易斯（Gilbert N. Lewis）、梅尔·兰德尔（Merle Randall）[18] 和 E·A·古根海姆（E. A. Guggenheim）[19][20] 将吉布斯的数学方法应用于化学过程的分析。

4. 词源

　　 热力学有着复杂的词源学背景。[21]

　　 从表面分析来看，这个词由两个部分组成，可以追溯到古希腊语。首先，"thermo-"（"热的"；如在词汇 “温度计” 中使用）源自希腊词根 θέρμη (therme)，意为 “热”。其次，"dynamics"（"力学"或"动力学"）源自希腊词根 δύναμις (dynamis)，意为 “力量” 或 “动力”。[23]

　　 在 1849 年，威廉·汤姆森（William Thomson）使用了形容词 “thermo-dynamic”。[24][25]

　　 在 1854 年，汤姆森和威廉·兰金（William Rankine）使用名词 “thermo-dynamics” 来代表广义热机的科学。[25][21]

　　 皮埃尔·佩罗（Pierre Perrot）声称，热力学一词是由詹姆斯·焦耳（James Joule）在 1858 年创造的，用来指代热与动力之间关系的科学，[12] 然而，焦耳从未使用过该术语，而是使用了 “完美的热力学引擎” 这一表达，指代汤姆森在 1849 年使用的术语。[21]

5. 热力学分支

　　 热力学系统的研究发展出了几个相关的分支，每个分支都使用不同的基本模型作为理论或实验基础，或将热力学原理应用于不同类型的系统。

经典热力学

　　 经典热力学是对接近平衡态的热力学系统状态的描述，它使用宏观的、可测量的属性。经典热力学用于基于热力学定律来建模能量、功和热的交换。形容词 “经典” 反映了这一学科在 19 世纪发展过程中所代表的第一层次的理解，描述了系统的变化，主要以宏观的经验（大尺度的、可测量的）参数来表达。后来，统计力学的发展为这些概念提供了微观的解释。

统计力学

　　 统计力学，也称为统计热力学，随着 19 世纪末和 20 世纪初原子与分子理论的发展而出现，并通过对单个粒子或量子力学状态之间微观相互作用的解释，补充了经典热力学。该领域将单个原子和分子的微观属性与材料的宏观、可观测的体积属性联系起来，从而解释了经典热力学作为统计学、经典力学和量子理论在微观层面的自然结果。

化学热力学

　　 化学热力学是研究能量与化学反应或物质相态变化之间关系的学科，在热力学定律的框架内进行。化学热力学的主要目标是确定某一转化过程的自发性。[26]

平衡热力学

　　 平衡热力学是研究物质和能量在系统或物体中的传递的学科，这些系统或物体可以通过外界因素的作用，从一个热力学平衡状态转变到另一个平衡状态。术语 “热力学平衡” 表示一种平衡状态，其中所有宏观流动均为零；对于最简单的系统或物体，其强度属性是均匀的，且其压力垂直于边界。在平衡状态下，系统的宏观不同部分之间没有未平衡的势能或驱动力。平衡热力学的一个核心目标是：在给定系统处于明确初始平衡状态的情况下，结合其周围环境和构成边界，计算在特定热力学操作改变其边界或周围环境后，系统将达到的最终平衡状态。

非平衡热力学

　　 非平衡热力学是热力学的一个分支，研究的是不处于热力学平衡状态的系统。自然界中大多数系统都不处于热力学平衡状态，因为它们不是静止状态，且不断地、间歇性地受到物质和能量的流动，向其他系统输入和输出。对非平衡系统的热力学研究需要比平衡热力学所涉及的更为一般的概念。[27] 许多自然系统至今仍超出了目前已知的宏观热力学方法的范围。

6. 热力学定律

图
图 2：原始 1824 年卡诺热机的注释彩色版本，显示了热体（锅炉）、工作体（系统，蒸汽）和冷体（水），字母标注根据卡诺循环中的停止点进行标示。

　　 热力学主要基于一组四个定律，当应用于符合每个定律所暗示的约束条件的系统时，这些定律是普遍有效的。在热力学的各种理论描述中，这些定律可能以看似不同的形式表达，但最突出的表述如下。

热力学零定律

　　 热力学零定律声明：如果两个系统分别与第三个系统处于热平衡状态，则它们也必然相互处于热平衡状态。

　　 这一声明意味着热平衡是一个等价关系，适用于所考虑的热力学系统集。系统被认为处于平衡状态，如果它们之间的小范围随机交换（例如布朗运动）不会导致能量的净变化。这个定律在每次温度测量中都被默认为成立。因此，如果想判断两个物体是否处于相同温度，不需要将它们接触在一起并测量它们的可观测属性随时间的变化。[28] 该定律为温度提供了一个经验定义，并为实际温度计的构造提供了依据。

　　 零定律最初并未被视为热力学的独立定律，因为它在热力学平衡的基础上已经隐含在其他定律中。第一、第二和第三定律已经明确提出，并在物理学界广泛接受，直到零定律在温度定义中的重要性被意识到。在重新编号其他定律不切实际的情况下，它被命名为零定律。

第一定律

图
图 3：开瓶时的起泡酒（高速摄影）。压力的突然下降导致温度急剧下降。空气中的水分凝结成冰，形成一阵微小冰晶的烟雾。[29][30][31]

　　 热力学第一定律声明：在没有物质转移的过程中，热力学系统的内能变化(\(\Delta U\))等于系统吸收的热量(\(Q\))减去系统对其周围环境所做的热力学功(\(W\))。[32][nb 1]

　　 \[ \Delta U = Q - W~ \]

　　 其中，(\(\Delta U\)) 表示封闭系统内能的变化（在该系统中，热量或功可以通过系统边界传递，但物质转移是不可能的）；(\(Q\)) 表示传递给系统的热能量；(\(W\)) 表示系统对周围环境做的热力学功。一个等价的陈述是，第一类永动机是不可能的；系统对其周围环境做的功 (\(w\)) 需要系统的内能 (\( U\)) 减少或被消耗，因此系统通过该功损失的内能必须通过外部能量源作为热量 (\( Q\)) 或通过外部机器对系统做功的方式补充（使得 (\( U\)) 得以恢复），以使系统能够持续工作。

　　 对于包含物质转移的过程，需要进一步的声明：在考虑到系统各自的基准参考状态的情况下，当两个系统（可能具有不同的化学组成）最初仅通过一堵不可渗透的墙隔开，并且在其他方面是孤立的，通过热力学操作（移除墙壁）将它们组合成一个新系统时，则有：

　　 \[ U_0 = U_1 + U_2~ \]

　　 其中，(\( U_0\)) 表示组合系统的内能，(\( U_1\))和 (\( U_2\)) 分别表示各自隔离系统的内能。

　　 在热力学中，这一定律是能量守恒原理的表达，该原理指出，能量可以被转化（从一种形式转变为另一种形式），但不能被创造或销毁。[33]

　　 内能是热力学状态的主要属性，而热量和功是能量转移的方式，通过这些方式，过程可能会改变系统的状态。系统内能的变化可以通过热量的加入或移除、以及对系统所做的功或系统所做的功的任何组合来实现。作为状态函数，内能不依赖于系统到达其状态的方式，或者中间步骤的路径。

第二定律

　　 热力学第二定律的传统版本声明：热量不会自发地从较冷的物体流向较热的物体。

　　 第二定律指的是物质和辐射的系统，最初在温度、压力、化学势能和其他强度属性上存在不均匀性，这些不均匀性可能是由于系统内部的 “约束” 或不可渗透的刚性壁壁，或外部施加的力引起的。该定律指出，当系统与外界及这些外部力隔离时，有一个确定的热力学量——熵，它会随着约束的去除而增加，最终在热力学平衡时达到最大值，此时不均匀性几乎消失。对于初始状态远离热力学平衡的系统，尽管已提出了若干个方案，但目前尚没有已知的普遍物理原则来确定趋向热力学平衡的速率，而热力学并不处理这种速率。第二定律的不同版本都表达了系统趋向热力学平衡过程中所涉及的过渡的普遍不可逆性。

　　 在宏观热力学中，第二定律是适用于任何实际热力学过程的基本观察；在统计热力学中，第二定律被假定为分子混乱的后果。

第三定律

　　 热力学第三定律声明：随着系统温度接近绝对零度，所有过程都将停止，系统的熵接近最小值。

　　 这一热力学定律是关于熵和达到绝对零度温度不可能性的统计性质定律。该定律为熵的确定提供了一个绝对参考点。相对于这个点确定的熵被称为绝对熵。另一种定义包括：“所有系统和系统所有状态的熵在绝对零度时最小”，或者等价地，“任何有限次过程都无法达到绝对零度”。

　　 绝对零度，如果可以实现的话，是所有活动停止的温度，具体为：−273.15 °C（摄氏度）、−459.67 °F（华氏度）、0 K（开尔文温度）或 0° R（兰氏度）。

7. 系统模型

图
图 4：一个通用热力学系统的示意图

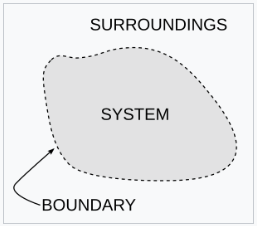
　　 热力学中的一个重要概念是热力学系统，它是一个在研究中精确定义的宇宙区域。宇宙中除了系统之外的所有事物都被称为环境。系统与宇宙的其余部分之间通过一个边界分隔开来，这个边界可以是物理的，也可以是概念上的，但它的作用是将系统限制在一个有限的体积内。边界的部分通常被描述为 “壁”，它们具有各自定义的 “透过性”。根据各自的透过性，系统与环境之间的能量（作为功或热量）或物质的转移是通过这些壁进行的。

　　 任何通过边界并引起系统内能变化的物质或能量，都需要在能量平衡方程中进行考虑。由壁所围成的体积可以是围绕一个单一原子共振能量的区域，例如麦克斯·普朗克在 1900 年所定义的；也可以是蒸汽机中的蒸汽或空气体积，例如萨迪·卡诺在 1824 年所定义的。该系统也可以仅仅是一个核素（即夸克系统），这是量子热力学中的假设。当采用更宽松的观点，且不再要求热力学平衡时，系统可以是热带气旋的主体，例如凯里·埃曼纽尔在 1986 年在大气热力学领域中的理论，或者是黑洞的事件视界。

　　 边界有四种类型：固定的、可移动的、真实的和虚拟的。例如，在一台发动机中，固定边界意味着活塞被锁定在其位置，在此位置内可能发生一个恒定体积的过程。如果允许活塞移动，那么这个边界就是可移动的，而气缸和气缸盖的边界是固定的。对于封闭系统，边界是真实的，而对于开放系统，边界通常是虚拟的。在喷气发动机的情况下，可以假设在发动机进气口处有一个固定的虚拟边界，沿着外壳表面有固定边界，排气喷嘴处有第二个固定的虚拟边界。

　　 通常，热力学将系统分为三类，依据其允许穿越边界的物质和能量类型：

表1：热力学系统的相互作用
系统类型 质量流动 功 热
开放系统 ✔ ✔ ✔
封闭系统 ✘ ✔ ✔
热隔离系统 ✘ ✔ ✘
机械隔离系统 ✘ ✘ ✔
孤立系统 ✘ ✘ ✘

　　 随着时间的推移，在孤立系统中，内部的压力、密度和温度差异趋于平衡。所有均衡过程完成后，系统被称为处于热力学平衡状态。

　　 一旦达到热力学平衡，系统的性质在时间上将保持不变。相比于非平衡系统，平衡状态下的系统更简单且易于理解。通常，在分析一个动态热力学过程时，会做出简化假设，即过程中的每个中间状态都处于平衡状态，从而形成发展极为缓慢的热力学过程，使每一步中间状态都是平衡状态，这种过程称为可逆过程。

8. 状态和过程

　　 当系统在一组给定条件下处于平衡时，就称其处于确定的热力学状态。系统的状态可以通过一系列状态量来描述，这些状态量不依赖于系统达到该状态的过程。根据系统大小变化时这些量的变化方式，它们被称为强度变量或广度变量。系统的性质可以通过状态方程来描述，状态方程规定了这些变量之间的关系。状态可以被视为一组固定变量下对系统的瞬时定量描述。

　　 热力学过程可以定义为热力学系统从初始状态到最终状态的能量演变过程。它可以通过过程量来描述。通常，每个热力学过程根据固定的参数（如温度、压力或体积等）在能量特征上与其他过程区别开来；此外，将这些过程分成对是有用的，在这些对中，每个被固定的变量都是共轭对的一员。

　　 几种常见的热力学过程包括：

9. 仪器

　　 热力学仪器有两种类型，即计量仪和储热库。热力学计量仪是任何用于测量热力学系统参数的设备。在某些情况下，热力学参数实际上是以理想化的测量仪器来定义的。例如，零定律指出，如果两个物体与第三个物体处于热平衡状态，那么它们彼此也处于热平衡状态。正如詹姆斯·麦克斯韦在 1872 年指出的，这一原理表明可以测量温度。理想化的温度计是一个在恒定压力下的理想气体样本。根据理想气体定律 \( pV = nRT \)，这种样本的体积可以用作温度的指示器；以这种方式定义了温度。尽管压力是通过机械方式定义的，但可以通过恒温的理想气体样本构建一个测量压力的装置，称为气压计。量热计是一种用于测量和定义系统内能的装置。

　　 热力学储热库是一个系统，其体积足够大，以至于当它与所研究的系统接触时，其状态参数几乎不会显著改变。当储热库与系统接触时，系统会与储热库达到平衡。例如，压力储热库是处于特定压力的系统，它将这种压力施加到与其机械连接的系统上。地球大气层通常用作压力储热库。海洋在为发电厂冷却时可以充当温度储热库。

10. 共轭变量

　　 主条目：共轭变量 热力学的核心概念是能量，即做功的能力。根据第一定律，系统及其环境的总能量是守恒的。能量可以通过加热、压缩或加入物质的方式传入系统，也可以通过冷却、膨胀或提取物质的方式从系统中提取出来。例如，在力学中，能量的传递等于施加在物体上的力与由此产生的位移的乘积。

　　 共轭变量是成对的热力学概念，其中第一个类似于作用在某热力学系统上的 “力”，第二个类似于由此产生的 “位移”，二者的乘积等于传递的能量。常见的共轭变量包括：

11. 热力学势

　　 热力学势是系统中储存能量的不同定量测量方式。热力学势用于测量系统从初始状态演变到最终状态的能量变化。所使用的势取决于系统的约束条件，例如恒温或恒压。例如，亥姆霍兹能和吉布斯能分别是在温度和体积固定或压力和温度固定时系统中可用于做功的能量。热力学势无法在实验室中直接测量，但可以通过分子热力学计算得到。[34][35]

表2：五个最著名的热力学势为：
名称 符号 公式 自然变量
内能 \( U \) \( \int \left( T \, dS - p \, dV + \sum_i \mu_i \, dN_i \right) \) \( S, V, \{N_i\} \)
亥姆霍兹自由能 \( F \) \( U - TS \) \( T, V, \{N_i\} \)
焓 \( H \) \( U + pV \) \( S, p, \{N_i\} \)
吉布斯自由能 \( G \) \( U + pV - TS \) \( T, p, \{N_i\} \) |
朗道势或大势 \( \Omega, \Phi_G \) \( U - TS - \sum_i \mu_i N_i \) \( T, V, \{\mu_i\} \)

　　 其中，\( T \) 是温度，\( S \) 是熵，\( p \) 是压力，\( V \) 是体积，\( \mu \) 是化学势，\( N \) 是系统中的粒子数，\( i \) 是系统中粒子种类的计数。

　　 热力学势可以从应用于热力学系统的能量平衡方程中推导出来。其他热力学势也可以通过勒让德变换获得。

12. 公理化热力学

　　 公理化热力学是一门数学学科，旨在通过严格的公理来描述热力学，例如，找到一种严格的数学方式来表达熟悉的热力学定律。

　　 首次尝试公理化热力学理论的是康斯坦丁·卡拉西奥多里（Constantin Carathéodory）在 1909 年的著作《热力学基础研究》，该书利用了 Pfaff 系统和绝热可达性概念，这是卡拉西奥多里自己引入的概念。[36][37] 在这种表述中，热、熵和温度等热力学概念是从更直接可测量的量中推导出来的。[38] 后来的理论不同之处在于它们假设热力学过程具有任意的初始和最终状态，而不是仅考虑相邻状态。

13. 应用领域

14. 另请参见

列表和时间线

15. 注释

  1. 该符号约定（\(Q\) 表示供应给系统的热量，\(W\) 表示系统对外做的功）采用的是鲁道夫·克劳修斯的约定。相反的符号约定通常用于化学热力学。

16. 参考文献

　　
1. Clausius, Rudolf (1850). 热的动力及其对热理论可推导出的定律。Poggendorff's Annalen der Physik, LXXIX (Dover 再版)。ISBN 978-0-486-59065-3。
2. William Thomson, LL.D. D.C.L., F.R.S. (1882). 数学与物理论文。第一卷。伦敦，剑桥：C.J. Clay, M.A. & Son, 剑桥大学出版社。第 232 页。ISBN 978-0-598-96004-7。2021 年 4 月 18 日从原始版本存档。2020 年 11 月 2 日检索。
3. Clausius, R. (1867). 热的机械理论——及其在蒸汽机和物体物理特性中的应用。伦敦：John van Voorst。2012 年 6 月 19 日检索。版本：PwR_Sbkwa8IC。包含他许多其他作品的英文翻译。
4. Clausius, RJE (1870). 关于一个适用于热的机械定理。《哲学杂志》，第四系列，40: 122–127。
5. Van Ness, H.C. (1983) [1969]. 理解热力学。Dover 出版社。ISBN 9780486632773。OCLC 8846081。
6. Dugdale, J.S. (1998). 熵及其物理意义。Taylor and Francis。ISBN 978-0-7484-0569-5。OCLC 36457809。
7. Smith, J.M.; Van Ness, H.C.; Abbott, M.M. (2005). 化学工程热力学导论(PDF). 第 27 卷（第 7 版），第 584 页。Bibcode:1950JChEd..27..584S. doi:10.1021/ed027p584.3. ISBN 978-0-07-310445-4。OCLC 56491111. {{cite book}}: |journal= 忽略(help)。
8. Haynie, Donald T. (2001). 生物热力学。剑桥大学出版社。ISBN 978-0-521-79549-4。OCLC 43993556。
9. 热力学学派*于 2017 年 12 月 7 日存档于 Wayback Machine – EoHT.info。 10. Partington, J.R. (1989). 化学简史。Dover 出版社。OCLC 19353301。 11. 纽科门发动机从 1711 年开始被改进，直到瓦特的工作，使得效率比较需要进行限定，但与 1865 年版本相比，效率提高约 100%。
12. Perrot, Pierre (1998). 热力学词典。牛津大学出版社。ISBN 978-0-19-856552-9。OCLC 123283342。
13. Cengel, Yunus A.; Boles, Michael A. (2005). 热力学——工程方法。McGraw-Hill 出版社。ISBN 978-0-07-310768-4。
14. Cardwell, D.S.L. (1971), 从瓦特到克劳修斯：早期工业时代热力学的兴起，伦敦：Heinemann，ISBN 978-0-435-54150-7。
15. Gibbs, Willard, J. (1874–1878). 康涅狄格艺术与科学学院学报，第三卷，新黑文，第 108–248 页，343–524 页。
16. Gibbs, Willard (1993). J. Willard Gibbs 的科学论文，第一卷：热力学，Ox Bow Press。ISBN 978-0-918024-77-0。OCLC 27974820。
17. Duhem, P.M.M. (1886). 热力学势及其应用，巴黎：Hermann 出版社。
18. Lewis, Gilbert N.; Randall, Merle (1923). 热力学与化学物质的自由能，McGraw-Hill 出版社。
19. Guggenheim, E.A. (1933). J.W.吉布斯方法的现代热力学，Methuen 出版社，伦敦。
20. Guggenheim, E.A. (1949/1967). 热力学：化学家和物理学家的高级处理，第一版 1949 年，第五版 1967 年，北荷兰出版社，阿姆斯特丹。
21. 热力学（词源）。EoHT.info。2023 年 10 月 29 日存档。2023 年 10 月 29 日检索。
22. Thompson, Silvanus (1910). 威廉·汤姆森的生平：拉格斯的开尔文男爵，第一卷。MacMillan and Co., Limited，第 241 页。自然哲学的基本主题是动力学，或称力的科学……自然界中的每一个现象都是力的表现。
23. Donald T. Haynie (2008). 生物热力学（第二版）。剑桥大学出版社，第 26 页。
24. Kelvin, William T. (1849) 卡诺热动力理论的描述——以及从雷诺蒸汽实验中推导出的数值结果。《爱丁堡皇家学会学报》，第 XVI 卷。1 月 2 日。扫描版存档于 2017 年 7 月 24 日，Wayback Machine。
25. Smith, Crosbie W. (1977). 威廉·汤姆森与热力学的创立：1840-1855。《精确科学史档案》，16(3): 231–288。doi:10.1007/BF00328156。ISSN 0003-9519。JSTOR 41133471。S2CID 36609995。
26. Klotz, Irving (2008). 化学热力学：基本理论与方法。新泽西州霍博肯：John Wiley & Sons, Inc. 第 4 页。ISBN 978-0-471-78015-1。
27. Pokrovskii, Vladimir (2020). 复杂系统的热力学：原理与应用。IOP 出版社，英国布里斯托尔。Bibcode:2020tcsp.book.....P。
28. Moran, Michael J. 和 Howard N. Shapiro, 2008。工程热力学基础。第 6 版。Wiley and Sons: 16。
29. 起泡酒，香槟及其相关产品 - 第 2 部分。起泡酒，香槟及其相关产品。Chemistry Europe (chemistryviews.org)。2010 年 12 月 17 日。2023 年 4 月 17 日检索。
30. Klaus Roth: Sekt, Champagner & Co. 在化学我们的时代中的如此迷人的化学，2009 年 12 月 8 日：《化学我们的时代》，第 43 卷，第 6 期，第 418-432 页，doi:10.1002/ciuz.200900520。
31. Klaus Roth: 化学美食，Wiley-VCH 出版社，2010 年，ISBN 978-3527327522，第 47 页。
32. Bailyn, M. (1994). 热力学概论，美国物理学会，AIP 出版社，纽约伍德伯里，ISBN 0883187973，第 79 页。
33. Callen, H.B. (1960/1985). 热力学与统计热力学入门（第二版），John Wiley & Sons，纽约霍博肯，ISBN 9780471862567，第 11–13 页。
34. Graben, H.W.; Ray, John R. (1993 年 12 月 10 日). "热力学、统计力学和计算机模拟的八个物理系统"。《分子物理学》, 80 (5): 1183–1193. Bibcode:1993MolPh..80.1183G. doi:10.1080/00268979300102971. ISSN 0026-8976。
35. Nitzke, Isabel; Stephan, Simon; Vrabec, Jadran (2024 年 6 月 3 日). "使用物理模型的热力学势拓扑：亥姆霍兹、吉布斯、大势和零势"。《化学物理学报》, 160 (21). Bibcode:2024JChPh.160u4104N. doi:10.1063/5.0207592. ISSN 0021-9606. PMID 38828811。
36. Carathéodory, C. (1909). "关于热力学基础的研究"。《数学年鉴》（德文）, 67 (3): 355–386. doi:10.1007/BF01450409. ISSN 0025-5831. S2CID 118230148。
37. Frankel, Theodore (2004). 物理学的几何学：导论（第二版），剑桥大学出版社，ISBN 9780521539272。
38. Rastall, Peter (1970 年 10 月 1 日). "简化的经典热力学"。《数学物理学杂志》, 11 (10): 2955–2965. Bibcode:1970JMP....11.2955R. doi:10.1063/1.1665080. ISSN 0022-2488。

17. 延伸阅读

以下书籍更具技术性：


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利