欧姆定律（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

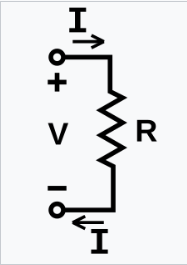
　　 欧姆定律指出，通过导体的电流与其两端的电压成正比。引入比例常数 “电阻” 后，[1] 可以得到描述这种关系的三个数学公式：[2] \[ V = IR \quad \text{或} \quad I = \frac{V}{R} \quad \text{或} \quad R = \frac{V}{I}~ \] 其中，\(I\) 是通过导体的电流，\(V\) 是测量的导体两端的电压，\(R\) 是导体的电阻。更具体地说，欧姆定律指出，这个关系中的 \(R\) 是常数，独立于电流。[3] 如果电阻不是常数，那么之前的公式就不能称为欧姆定律，但它仍然可以作为静态/直流电阻的定义。[4] 欧姆定律是一个经验关系，准确描述了绝大多数电导材料在多个数量级的电流下的导电性。然而，一些材料不遵守欧姆定律，这些材料被称为非欧姆材料。

　　 该定律以德国物理学家 Georg Ohm 的名字命名，他在 1827 年发表的一篇论文中，描述了通过包含不同长度电线的简单电路的施加电压和电流的测量。欧姆用一个比现代形式稍微复杂的方程来解释他的实验结果（参见下文的 “历史” 部分）。

　　 在物理学中，欧姆定律一词也用于指代该定律的各种推广；例如，在电磁学和材料科学中使用的欧姆定律的矢量形式： \[ \mathbf{J} = \sigma \mathbf{E},~ \] 其中 \( \mathbf{J} \) 是在某一位置的电流密度，\( \mathbf{E} \) 是该位置的电场，\( \sigma \)（希腊字母西格玛）是一个依赖于材料的参数，称为导电率，定义为电阻率 \( \rho \)（希腊字母罗）的倒数。这个欧姆定律的重新表述是由古斯塔夫·基尔霍夫（Gustav Kirchhoff）提出的。[5]

1. 历史

　　 在 1781 年，乔治·欧姆的工作之前，亨利·卡文迪许进行了实验，使用了不同直径和长度的莱顿瓶和玻璃管，填充了盐溶液。他通过注意完成电路时身体感受到的电击强度来测量电流。卡文迪许写道，“速度”（电流）与 “电气化程度”（电压）成正比。当时，他没有将结果与其他科学家分享，[6] 直到詹姆斯·克拉克·麦克斯韦在 1879 年发布了这些结果。[7]

　　 弗朗西斯·罗纳兹在 1814 年使用金叶电计，划分了 “强度”（电压）和 “量”（电流）在干电堆（一种高电压源）中的关系。他发现，在某些气象条件下，干电堆中两者之间的关系并不是成正比的。[8][9]

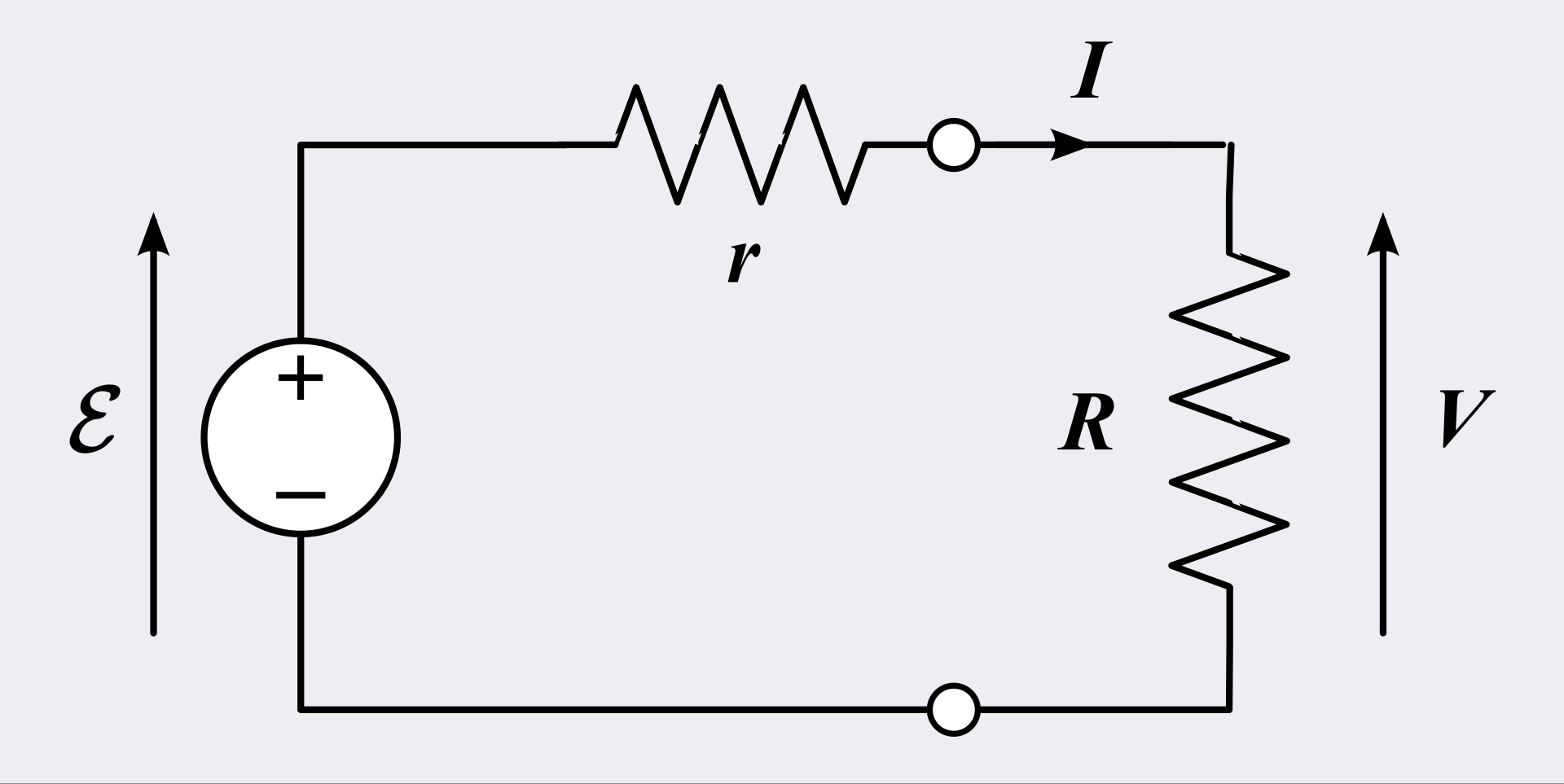
　　 欧姆于 1825 年和 1826 年进行电阻的研究，并于 1827 年将其结果出版为《Die galvanische Kette, mathematisch bearbeitet》（《电化学电路的数学分析》）。[10] 他在理论解释中受到了约瑟夫·傅里叶在热传导方面研究的很大启发。在实验中，欧姆最初使用了伏打电堆，但后来改用热电偶，因为热电偶在内阻和恒定电压方面提供了更稳定的电压源。他使用了电流计来测量电流，并知道热电偶接点之间的电压与接点温度成正比。然后，他加入了不同长度、直径和材料的测试导线以完成电路。他发现他的数据可以通过以下方程建模： \[ x = \frac{a}{b + \ell}~\] 其中 \( x \) 是电流计的读数，\( \ell \) 是测试导体的长度，\( a \) 取决于热电偶接点温度，\( b \) 是整个系统的常数。由此，欧姆得出了他的比例定律并公布了他的结果。

　　 用现代符号表示，我们可以写为： \[ I = \frac{\mathcal{E}}{r + R}~ \] 其中，\(\mathcal{E}\) 是热电偶的开路电动势，\(r\) 是热电偶的内阻，\(R\) 是测试电线的电阻。根据电线的长度，这可以表示为： \[ I = \frac{\mathcal{E}}{r + \mathcal{R}\ell}~ \] 其中，\(\mathcal{R}\) 是测试电线每单位长度的电阻。这样，欧姆定律的系数为： \[ a = \frac{\mathcal{E}}{\mathcal{R}}, \quad b = \frac{\mathcal{r}}{\mathcal{R}}.~ \]

　　 欧姆定律可能是最早的、描述电学物理现象的重要定量定律之一。今天，我们几乎认为它是显而易见的。然而，当欧姆首次发表他的研究成果时，情况并非如此；当时的批评者对他所阐述的内容表现出敌对态度。他们称他的工作是 “一张赤裸裸的幻想网”，而且教育部长宣称，“一位传播这种异端思想的教授不配教授科学”。当时德国的主流科学哲学认为，自然界的规律是井然有序的，因而不需要通过实验来理解自然，科学真理可以通过推理得出。再者，欧姆的兄弟马丁，一位数学家，也在与德国教育体制作斗争。这些因素阻碍了欧姆的研究成果的接受，直到 1840 年代，他的工作才广泛被接受。然而，欧姆在去世之前就因其对科学的贡献获得了认可。

　　 到了 1850 年代，欧姆定律已被广泛知晓并被认为是经过证实的。诸如 “巴洛定律” 等替代理论被淘汰，尤其是在电报系统设计的实际应用中，正如塞缪尔·摩尔斯在 1855 年所讨论的那样。

　　 1897 年，J.J.汤姆森发现了电子，并很快意识到电子是电路中携带电流的粒子（电荷载体）。1900 年，保罗·德鲁德提出了第一个（经典的）电导模型——德鲁德模型，最终为欧姆定律提供了科学解释。在这个模型中，固体导体由静止的原子晶格（离子）构成，导电电子在其中随机运动。施加电压在导体上形成电场，使电子在电场方向上加速，导致电子的漂移，从而产生电流。然而，电子与原子发生碰撞，导致它们散射并使运动变得随机，从而将动能转化为热能（热能）。通过使用统计分布，可以证明电子的平均漂移速度，进而电流，与电场成正比，并且在较大范围的电压下，电流和电压也呈线性关系。

　　 1920 年代量子力学的发展稍微改变了这一模型，但在现代理论中，电子的平均漂移速度仍然可以被证明与电场成正比，从而导出了欧姆定律。1927 年，阿诺德·索末菲德将量子费米-狄拉克分布应用于德鲁德模型，得出了自由电子模型。一年后，费利克斯·布洛赫证明了电子在固体晶格中以波动的形式（布洛赫电子）运动，因此，德鲁德模型中假设的电子与晶格原子散射的过程并非主要过程；电子主要与杂质原子和材料中的缺陷发生散射。最终的继任者——现代的固体量子能带理论表明，固体中的电子不能像德鲁德模型中假设的那样吸收任意能量，而是被限制在能带内，能带之间存在禁带，电子不能具有禁带中的能量。能带间隙的大小是物质的特征，与其电阻率密切相关，解释了为什么有些物质是电导体，有些是半导体，而有些则是绝缘体。

　　 尽管电导的旧单位 “摩”（电阻单位欧姆的倒数）仍然在使用，但在 1971 年，新的单位 “西门子” 被采用，以此来纪念恩斯特·维尔纳·冯·西门子。正式论文中更倾向于使用 “西门子” 单位。

　　 1920 年代，研究发现，实际电阻器中的电流会存在统计波动，这些波动与温度有关，即使电压和电阻保持完全恒定；这种波动现在被称为约翰逊–奈奎斯特噪声，源于电荷的离散性质。这种热效应意味着，当电流和电压的测量时间足够短时，测得的 V/I 比值会与通过时间平均或集体平均测量电流所得到的 R 值发生波动；但在普通电阻材料的情况下，欧姆定律仍然适用于平均电流。

　　 欧姆的工作远早于麦克斯韦方程和对交流电路频率依赖效应的任何理解。现代电磁理论和电路理论的发展，在适当的限制条件下并不与欧姆定律相冲突。

2. 适用范围

　　 欧姆定律是一个经验定律，来自许多实验的归纳，这些实验表明，对于大多数材料，电流大致与电场成正比。它不如麦克斯韦方程那样基本，并且并不总是成立。任何给定的材料在强电场下都会崩溃，一些在电气工程中有用的材料在弱电场下是 “非欧姆” 的。[15][16]

　　 欧姆定律已经在不同的长度尺度上得到了验证。20 世纪初，人们曾认为欧姆定律在原子尺度下会失效，但实验结果并未验证这一预期。到 2012 年，研究人员已经证明，欧姆定律适用于宽度仅为四个原子、高度为一个原子的硅线。[17]

3. 微观起源

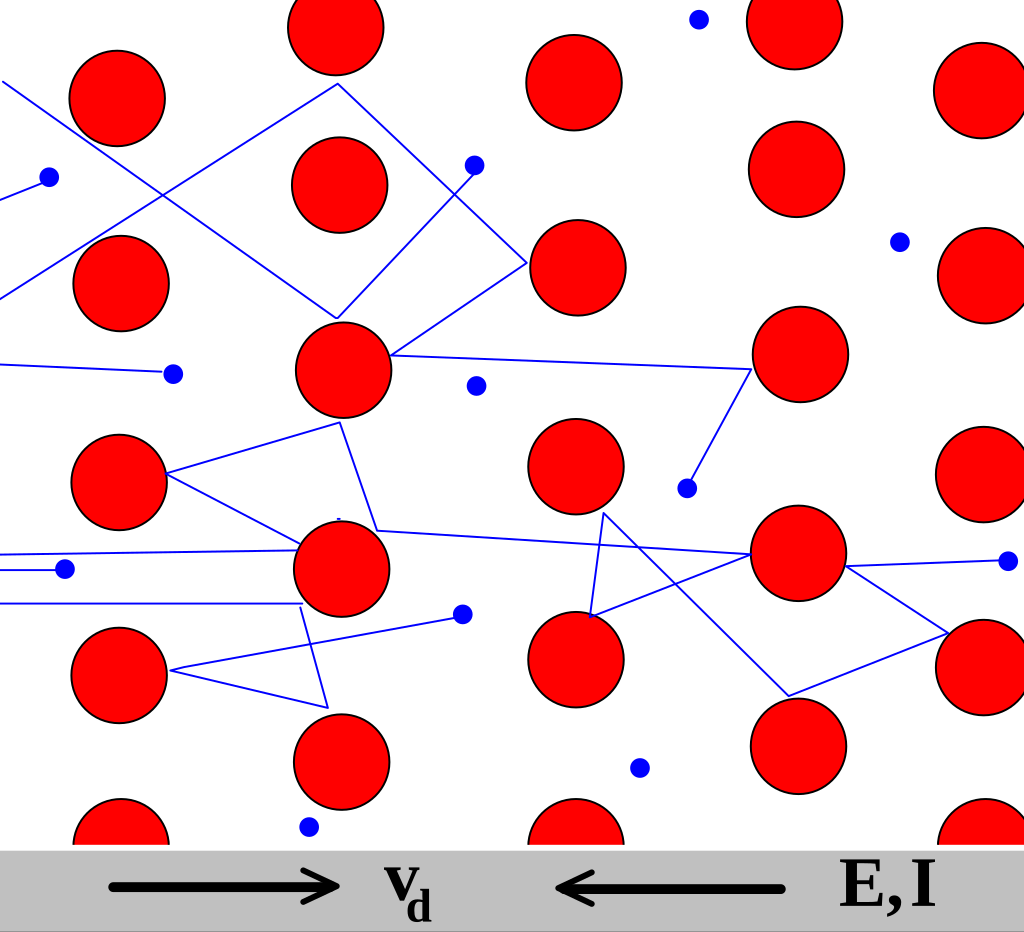
　　 电流密度对施加的电场的依赖本质上是量子力学性质的（参见经典与量子导电性）。基于经典力学的定性描述，欧姆定律可以通过保罗·德鲁德（Paul Drude）于 1900 年提出的德鲁德模型来推导。[18][19]

　　 德鲁德模型将电子（或其他载流子）视为在材料结构中与离子碰撞的弹球。电子会在电场的作用下沿电场的反方向加速。每次碰撞时，电子都会在随机方向上发生偏转，其速度远大于电场所提供的加速速度。最终的结果是，电子由于碰撞而采取锯齿形路径，但通常会朝着与电场方向相反的方向漂移。

　　 漂移速度决定了电流密度及其与电场的关系，并且与碰撞无关。德鲁德通过公式 \( p = -eE\tau \) 计算了电子的平均漂移速度，其中 \( p \) 是平均动量，\( -e \) 是电子的电荷，\( \tau \) 是平均碰撞时间。由于动量和电流密度都与漂移速度成正比，因此电流密度与施加的电场成正比；这就得出了欧姆定律。

4. 水力类比

　　 有时使用水力类比来描述欧姆定律。水压（以帕斯卡（Pa）或每平方英寸磅（PSI）为单位）是电压的类比，因为在管道的两个点之间建立水压差会导致水流动。水流量（例如以每秒升数计）是电流的类比，电流是以每秒库仑数计的。最后，流量限制器——例如放置在管道中测量水压的点之间的孔口——是电阻器的类比。我们说，水流通过孔口限制器的流速与孔口两端的水压差成正比。类似地，电流通过电阻器的电荷流速与电阻器两端的电压差成正比。更一般地，水力头可以看作是电压的类比，这样欧姆定律就类似于达西定律，后者将水力头与水流量通过水力导热性联系起来。

　　 通过水力欧姆类比，可以在流体流动网络中计算流量和压力变量。[20][21] 该方法可应用于稳态流动和瞬态流动情况。在线性层流区域，泊肃叶定律描述了管道的水力阻力，但在湍流区域，压力与流量的关系变为非线性。

　　 欧姆定律的水力类比已被用来近似描述血液在循环系统中的流动。[22]

5. 电路分析

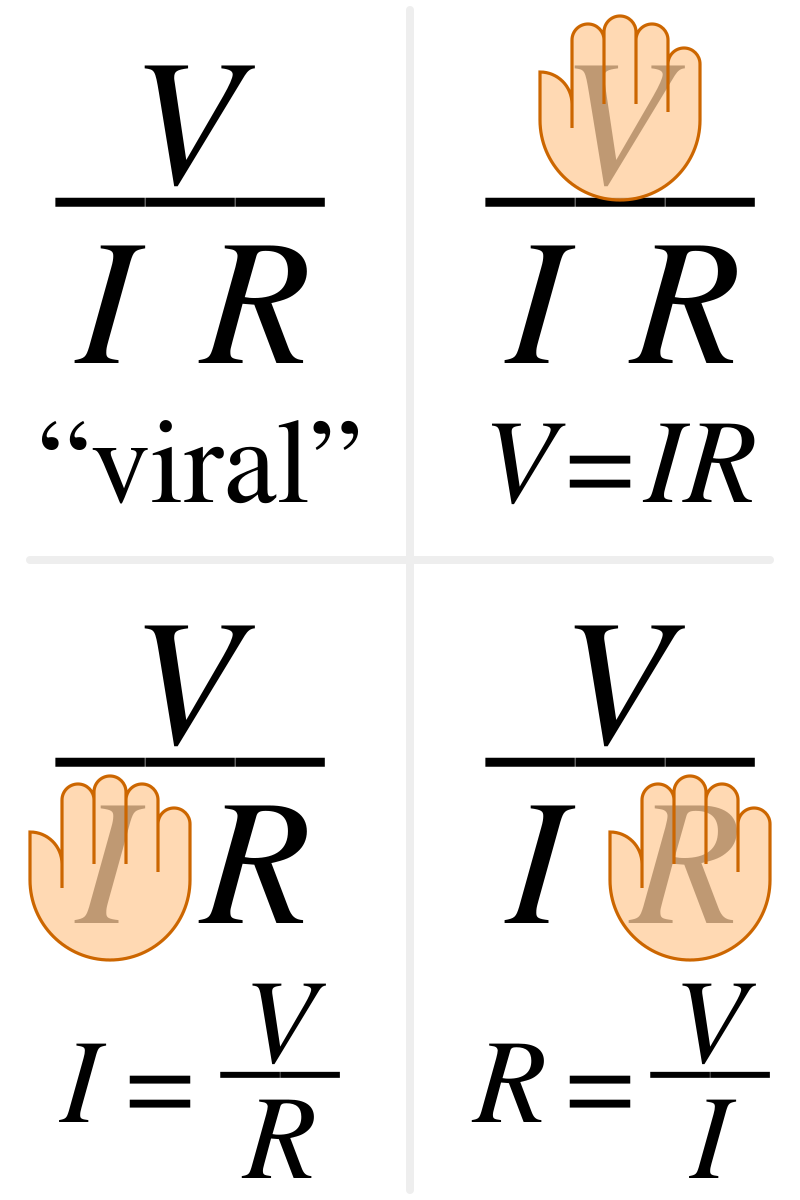
　　 在电路分析中，欧姆定律的三个等效表达式可互换使用： \[ I = \frac{V}{R} \quad \text{或} \quad V = IR \quad \text{或} \quad R = \frac{V}{I}~ \] 每个方程都有一些来源引用为欧姆定律的定义关系，[2][23][24] 或者引用全部三个方程，[25] 或者从比例形式推导出来，[26] 甚至有时只给出与欧姆原始表述不相符的两个方程。[27][28]

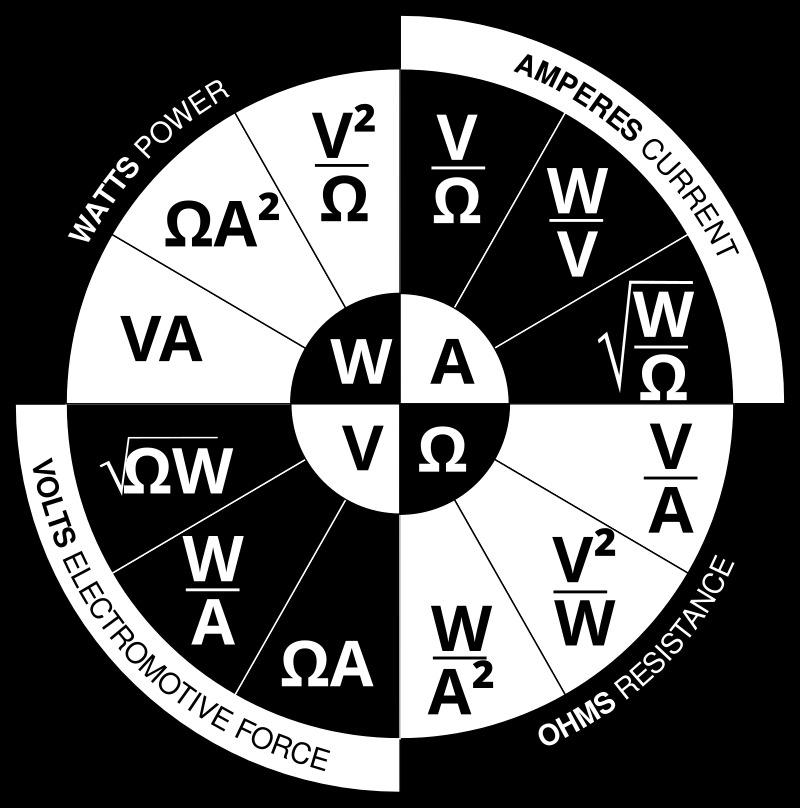
　　 这些方程的互换性可以通过一个三角形表示，其中 V（电压）位于顶部部分，I（电流）位于左侧部分，R（电阻）位于右侧部分。顶部和底部之间的分隔线表示除法（因此也称为除法条）。

电阻电路

　　 电阻是电路元件，它们根据欧姆定律阻碍电荷通过，并设计有特定的电阻值 R。在原理图中，电阻通常表示为一个长矩形或锯齿形符号。根据欧姆定律在某些工作范围内表现的元件（电阻器或导体）被称为欧姆元件（或欧姆电阻器），因为欧姆定律和一个单一的电阻值足以描述该元件在该范围内的行为。

　　 欧姆定律适用于仅包含电阻元件（没有电容或电感）的电路，无论驱动电压或电流是恒定的（直流）还是时间变化的（交流）。在任何时刻，欧姆定律对这样的电路都是有效的。

　　 串联或并联的电阻可以合并为一个 “等效电阻”，以便在分析电路时应用欧姆定律。

带有时变信号的反应性电路

　　 当电路中涉及电容器、电感器或传输线等反应性元件，并且施加交流（AC）或时变电压或电流时，电压和电流之间的关系变成一个微分方程的解，因此欧姆定律（如上所定义）并不直接适用，因为该形式只包含具有电阻值 R 的电阻，而不是可能包含电容（C）或电感（L）的复杂阻抗。

　　 时间不变的交流电路的方程与欧姆定律具有相同的形式。然而，这些变量被推广为复数，并且电流和电压波形是复指数函数。

　　 在这种方法中，电压或电流波形的形式为 Aest，其中 t 是时间，s 是复数参数，A 是复数标量。在任何线性时不变系统中，所有的电流和电压都可以用相同的 s 参数表示为系统的输入，从而消除时变复指数项，系统可以代数化地用电流和电压波形中的复数标量来描述。

　　 电阻的复杂推广是阻抗，通常用 Z 表示；可以证明，对于电感器： \[ Z = sL~ \] 对于电容器： \[ Z = \frac{1}{sC}~ \] 现在我们可以写出： \[ V = Z I~ \] 其中 V 和 I 分别是电压和电流中的复数标量，Z 是复杂阻抗。

　　 这种形式的欧姆定律，用 Z 代替 R，推广了简单的形式。当 Z 是复数时，只有实部负责消耗热量。

　　 在一般的交流电路中，Z 随着频率参数 s 的变化而强烈变化，因此电压和电流之间的关系也会变化。

　　 对于常见的稳态正弦波情况，s 参数取为 \( j\omega \)，对应于复正弦波：\(Ae^{j\omega t}\) 这种复电流和电压波形的实部描述了电路中的实际正弦电流和电压，由于不同的复数标量，它们可能处于不同的相位。

线性近似

　　 另见：小信号建模和网络分析（电路）§ 小信号等效电路

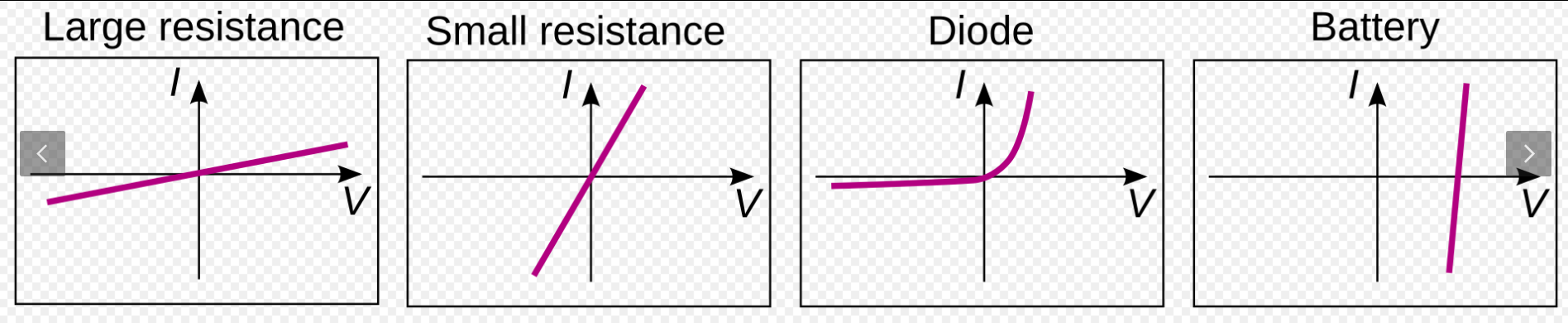
　　 欧姆定律是分析电路时使用的基本方程之一。它适用于金属导体和专门为此行为设计的电路元件（如电阻器）。这些元件在电气工程中无处不在。遵循欧姆定律的材料和元件被称为 “欧姆型”（ohmic），这意味着它们在施加的电压（V）或电流（I）的值和无论是直流（DC）还是交流（AC）电压/电流的极性如何的情况下，都能产生相同的电阻值（R = V/I）。

　　 在一个真正的欧姆型设备中，无论施加的电压 V 的值是多少，从公式 R = V/I 计算出来的电阻值始终是相同的。也就是说，V/I 的比值是恒定的，当电流与电压的关系被绘制成图时，曲线是直线（线性关系）。如果将电压强制设置为某个值 V，那么该电压 V 除以测得的电流 I 将等于 R。或者，如果将电流强制设置为某个值 I，那么测得的电压 V 除以该电流 I 也是 R。由于 I 与 V 的关系图是直线，那么对于施加在给定电阻 R 上的任何一对不同的电压 V1 和 V2，产生的电流 I1 = V1/R 和 I2 = V2/R，其比值 (V1 − V2)/(I1 − I2) 也将是一个常数，等于 R。运算符 “delta”（Δ）用于表示一个量的差异，因此我们可以写成ΔV = V1 − V2 和ΔI = I1 − I2。总结来说，对于任何具有电阻 R 的真正欧姆型设备，V/I = ΔV/ΔI = R，无论施加的电压、电流，还是任何施加的电压或电流的差异。

　　 然而，电路中有一些元件不遵循欧姆定律；也就是说，它们的电流与电压之间的关系（即 I–V 曲线）是非线性的（或称为非欧姆型）。一个例子是 p–n 结二极管（右图所示）。如图所示，对于二极管，电流并不会随着施加的电压线性增加。可以根据曲线为给定的施加电压（V）值确定电流（I）值，但不能通过欧姆定律来确定，因为 “电阻” 的值并不是施加电压的函数，而是变化的。此外，电流只有在施加电压为正时才会显著增加，而施加负电压时电流几乎不增加。在非线性曲线的某一点上，V/I 的比值有时被称为静态电阻、弦电阻或直流电阻[31][32]，但如图所示，沿非线性曲线的不同点选择，总的 V 对 I 的比值会有所不同。这意味着在曲线上的某一点上的 “直流电阻” V/I 并不等于通过施加具有峰值幅度 ΔV 伏特或 ΔI 安培的交流信号，并在该曲线的相同点处测量 ΔV/ΔI 所得到的值。然而，在某些二极管应用中，施加到设备上的交流信号较小，可以通过分析电路中的动态、小信号或增量电阻来处理，该电阻定义为电压（即直流工作点）处 V–I 曲线的斜率的倒数（也就是电流相对于电压的导数的倒数）。对于足够小的信号，动态电阻使得可以通过计算直流工作点处 V–I 曲线的切线的斜率的倒数，近似计算欧姆定律的小信号电阻[33]。

6. 温度效应

　　 欧姆定律有时被表述为：“对于处于给定状态的导体，电动势与产生的电流成正比。” 也就是说，电阻，即施加的电动势（或电压）与电流的比值，“不随电流强度的变化而变化。” 其中，“给定状态” 通常解释为 “在恒定温度下”，因为材料的电阻率通常与温度有关。由于电流的传导与导体的焦耳加热相关，根据焦耳定律，导体在通过电流时可能会发生温度变化。因此，电阻对温度的依赖使得在典型实验装置中，电阻还依赖于电流，这使得以这种形式的定律难以直接验证。麦克斯韦和其他科学家在 1876 年提出了几种实验方法来测试该定律，并控制加热效应。[34] 通常，样品电阻的测量是在低电流下进行的，以防止焦耳加热。然而，即使是很小的电流也会导致样品接触点的加热（或冷却），这是由于佩尔帖效应。在样品接触点，温度会有所不同，且其差异与电流成线性关系。电路中的电压降还包括塞贝克热电动势，该效应同样与电流成线性关系。因此，即使在极小电流下，样品电阻也会存在热修正。[35] 这种修正的大小可能与样品电阻相当。[36]

7. 与热传导的关系

　　 欧姆定律预测了在电压差的作用下，电荷（即电流）在电导体中的流动；而让-巴普蒂斯特-约瑟夫·傅里叶的原理则预测了在温度差的作用下，热量在热导体中的流动。

　　 这两个现象可以用相同的方程描述，方程中的变量在这两种情况下有不同的含义。具体来说，通过解决一个热传导（傅里叶）问题，使用温度（驱动力）和热流（驱动量的流动速率，即热能）的变量，可以得到一个类似的电导问题（欧姆定律），其中电势（驱动力）和电流（驱动量的流动速率，即电荷）的变量也会被求解。

　　 傅里叶工作的基础是他对热导率的清晰概念和定义。他假设在其他条件相同的情况下，热流与温度梯度严格成正比。尽管这一假设在小温度梯度下无疑是成立的，但当实际材料（例如具有温度依赖的热导率的材料）受到大温度梯度时，严格的比例关系就会失效。

　　 在欧姆定律的表述中也做出了类似的假设：在其他条件相同的情况下，每个点的电流强度与电势梯度成正比。通过现代测量方法，我们可以更容易地测试电流流动是否与电势梯度成正比，这在电学中比在热学中更容易验证。

8. 其他版本

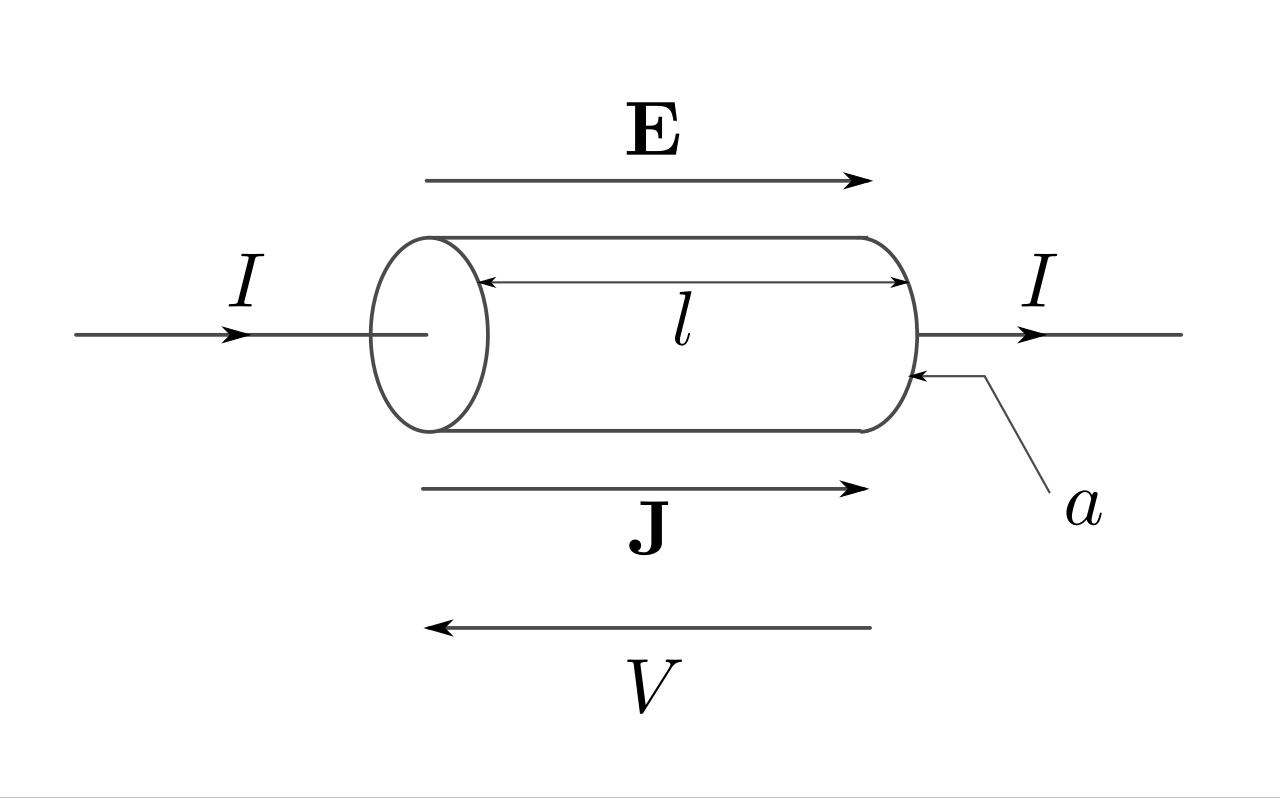
　　 欧姆定律（如上所述）在电气/电子工程领域是一个非常有用的方程，因为它描述了电压、电流和电阻如何在 “宏观” 层面上相互关联，也就是说，通常是作为电路中电路元件的行为。研究物质电学性质的物理学家在微观层面使用一个与欧姆定律密切相关且更一般的向量方程，有时也被称为欧姆定律，该方程的变量与欧姆定律中的标量变量 V、I 和 R 密切相关，但每个变量都是导体内位置的函数。物理学家通常使用欧姆定律的这种连续体形式：[37] \[ \mathbf {E} =\rho \mathbf {J}~ \] 其中，E 是电场向量，单位是伏特每米（类似于欧姆定律中的 V，单位是伏特），J 是电流密度向量，单位是安培每单位面积（类似于欧姆定律中的 I，单位是安培），ρ（rho）是电阻率，单位是欧姆·米（类似于欧姆定律中的 R，单位是欧姆）。上述方程也可以写作[38]： \[ J = \sigma E~ \] 其中，σ（sigma）是电导率，是电阻率 ρ 的倒数。

　　 两个点之间的电压定义为：[39] \[ \Delta V = - \int \mathbf{E} \cdot d\boldsymbol{\ell}~ \] 其中，\( d\boldsymbol{\ell} \) 是沿着电场向量 \( \mathbf{E} \) 积分路径的元素。如果施加的电场 \( \mathbf{E} \) 在导体长度方向上均匀且定向，如图所示，那么按照通常的约定，电压 \( V \) 方向与电场相反（见图），并且理解为电压 \( V \) 是沿导体长度的差分测量，从而我们可以去掉 \( \Delta \) 符号，以上的向量方程简化为标量方程： \[ V = E\ell \quad \text{或} \quad E = \frac{V}{\ell}~ \] 由于电场 \( E \) 在导线长度方向上是均匀的，假设导体的电阻率 \( \rho \) 一致，电流密度 \( J \) 在任何横截面上也将是均匀的，并且与导线长度方向一致，因此我们可以写为：[40] \[ J = \frac{I}{a}~ \] 将上述两个结果（分别针对 \( E \) 和 \( J \)）代入本节开头的连续体形式中： \[ \frac{V}{\ell} = \frac{I}{a}\rho \quad \text{或} \quad V = I \rho \frac{\ell}{a}~ \] 均匀导体的电阻用电阻率表示为：[40] \[ R = \rho \frac{\ell}{a}~ \] 其中，\( \ell \) 是导体的长度，单位为米（SI 单位），\( a \) 是横截面积（对于圆形导线，\( a = \pi r^2 \)，其中 \( r \) 是半径），单位为平方米，\( \rho \) 是电阻率，单位为欧姆·米。

　　 将上述方程中的 \( R \) 代入前面的方程后，适用于均匀电场（以及均匀电流密度）沿导体长度方向的欧姆定律的连续体形式简化为我们更熟悉的形式： \[ V = IR~ \] 一个完美的晶体结构，在足够低的热运动下且没有偏离周期性结构的情况下，应该没有电阻率[41]，但实际的金属中存在晶体缺陷、杂质、多种同位素以及原子的热运动。电子会与这些因素发生散射，从而导致流动的电阻。

　　 欧姆定律的更复杂的广义形式对凝聚态物理学非常重要，凝聚态物理学研究物质的性质，特别是其电子结构。广义来说，这些形式属于本构方程和传输系数理论的范畴。

磁效应

　　 如果外部磁场 \( \mathbf{B} \) 存在，并且导体不是静止的，而是以速度 \( \mathbf{v} \) 运动，那么必须增加一个额外的项来考虑洛伦兹力对载流子引起的电流。 \[ \mathbf{J} = \sigma (\mathbf{E} + \mathbf{v} \times \mathbf{B})~ \] 在运动导体的静止参考系中，这一项将消失，因为 \( \mathbf{v} = 0 \)。这没有矛盾，因为静止参考系中的电场与实验室参考系中的电场不同：\( \mathbf{E'} = \mathbf{E} + \mathbf{v} \times \mathbf{B} \)。电场和磁场是相对的，详见洛伦兹变换。

　　 如果电流 \( \mathbf{J} \) 是交流电流（因为施加的电压或电场随时间变化），则必须将反应性（电抗）加到电阻中，以考虑自感效应，见电气阻抗。如果频率很高或导体是线圈形状，电抗可能会很强。

导电流体

　　 在导电流体（例如等离子体）中，也有类似的效应。假设有一个流体以速度 \( \mathbf{v} \) 在磁场 \( \mathbf{B} \) 中运动，流体的相对运动会诱发电场 \( \mathbf{E} \)，该电场对带电粒子施加电力，产生电流 \( \mathbf{J} \)。对于电子气体，其粒子数密度为 \( n_e \)，其运动方程可以写成： \[ m_e n_e \frac{d \mathbf{v}_e}{dt} = -n_e e \mathbf{E} + n_e m_e \nu (\mathbf{v}_i - \mathbf{v}_e) - e n_e \mathbf{v}_e \times \mathbf{B}~ \] 其中，\( e \) 是电子的电荷，\( m_e \) 是电子的质量，\( \mathbf{v}_e \) 是电子的速度；\( \nu \) 是电子与离子碰撞的频率，\( \mathbf{v}_i \) 是离子的速度场。由于电子的质量远小于离子的质量，因此可以忽略上述方程的左侧，得到： \[ \sigma (\mathbf{E} + \mathbf{v} \times \mathbf{B}) = \mathbf{J}~ \] 在这里，我们使用了电流密度的定义，并且得出 \( \sigma = \frac{n_e e^2}{\nu m_e} \)，其中 \( \sigma \) 是电导率。该方程还可以等价地写为： \[ \mathbf{E} + \mathbf{v} \times \mathbf{B} = \rho \mathbf{J}~ \] 其中，\( \rho = \sigma^{-1} \) 是电阻率。也常常使用 \( \eta \) 来表示 \( \rho \)，但这可能会产生混淆，因为 \( \eta \) 也用于表示磁扩散率，定义为 \( \eta = \frac{1}{\mu_0 \sigma} \)。

9. 参见

• 菲克扩散定律
• 霍普金森定律（“磁性中的欧姆定律”）
• 最大功率传输定理
• 诺顿定理
• 电功率
• 片电阻
• 叠加定理
• 热噪声
• 戴维南定理

　　 用途

• LED-电阻电路

10. 参考文献

1. Consoliver, Earl L. & Mitchell, Grover I. (1920). 《汽车点火系统》. 麦格劳-希尔. 第 4 页.
2. Millikan, Robert A.; Bishop, E. S. (1917). 《电学原理》. 美国技术学会. 第 54 页.
3. Heaviside, Oliver (1894). 《电气论文》. 第 1 卷. 麦克米伦公司. 第 283 页. ISBN 978-0-8218-2840-3.
4. Young, Hugh; Freedman, Roger (2008). 《西尔斯和泽曼斯基的大学物理：现代物理学》. 第 2 卷（第 12 版）. 皮尔逊出版社. 第 853 页. ISBN 978-0-321-50121-9.
5. Darrigol, Olivier (2000 年 6 月 8 日). 《从安培到爱因斯坦的电动力学》. 克拉伦登出版社. 第 70 页. ISBN 9780198505945.
6. Fleming, John Ambrose (1911). “电学” . 收录于 Chisholm, Hugh (编). 《大英百科全书》. 第 9 卷（第 11 版）. 剑桥大学出版社. 第 182 页.
7. Bordeau, Sanford P. (1982). 《从伏特到赫兹——电力的兴起：从指南针到无线电，通过 16 位伟大科学家的著作，这些人的名字被用来衡量电力与磁学》. 伯吉斯出版社. 第 86-107 页. ISBN 9780808749080.
8. Ronalds, B. F. (2016). 《弗朗西斯·罗纳尔兹：电报的父亲》. 伦敦：帝国理工出版社. ISBN 978-1-78326-917-4.
9. Ronalds, B. F. (2016 年 7 月). “弗朗西斯·罗纳尔兹（1788–1873）：第一位电气工程师？”. 《IEEE 学报》. 第 104 卷（第 7 期）：1489–1498. DOI: [10.1109/JPROC.2016.2571358](https://doi.org/10.1109/JPROC.2016.2571358). S2CID 20662894.
10. Ohm, G. S. (1827). 《电流链的数学研究》. 柏林：T. H. Riemann. [原始文献](https://archive.org/details/...) 于 2009-03-26 归档 (PDF).
11. Davies, Brian (1980). “裸幻想之网？”. 《物理教育》. 第 15 卷（第 1 期）：57–61. Bibcode: [1980PhyEd..15...57D](https://doi.org/10.1088/...). S2CID 250832899.
12. Hart, Ivor Blashka (1923). 《科学创造者》. 伦敦：牛津大学出版社. 第 243 页. OL 6662681M.
13. Schnädelbach, Herbert (1984 年 6 月 14 日). 《1831-1933 年德国哲学》. 剑桥大学出版社. 第 78–79 页. ISBN 9780521296465.
14. Taliaferro Preston (1855). 《沙夫纳的电报指南：献给莫尔斯电报科学与艺术的著作》. 第 2 卷. Pudney & Russell.
15. Purcell, Edward M. (1985). 《电与磁学》, 伯克利物理课程，第 2 卷（第 2 版）, 麦格劳-希尔, 第 129 页, ISBN 978-0-07-004908-6.
16. Griffiths, David J. (1999). 《电动力学导论》（第 3 版）. 普伦蒂斯-霍尔出版社, 第 289 页, ISBN 978-0-13-805326-0.
17. Weber, B.; Mahapatra, S.; Ryu, H.; Lee, S.; Fuhrer, A.; Reusch, T. C. G.; Thompson, D. L.; Lee, W. C. T.; Klimeck, G.; Hollenberg, L. C. L.; Simmons, M. Y. (2012). “欧姆定律在原子尺度上的延续”. 《科学》. 第 335 卷（6064 期）：64–67. Bibcode: [2012Sci...335...64W](https://doi.org/10.1126/science.1214319). DOI: [10.1126/science.1214319](https://doi.org/10.1126/science.1214319). PMID 22223802. S2CID 10873901.
18. Drude, Paul (1900). “关于金属的电子理论”. 《物理年鉴》. 第 306 卷（3 期）：566–613. Bibcode: [1900AnP...306..566D](https://doi.org/10.1002/andp.19003060312). DOI: [10.1002/andp.19003060312](https://doi.org/10.1002/andp.19003060312). [失效链接].
19. Drude, Paul (1900). “关于金属的电子理论；第二部分：磁电效应和热磁效应”. 《物理年鉴》. 第 308 卷（11 期）：369–402. Bibcode: [1900AnP...308..369D](https://doi.org/10.1002/andp.19003081102). DOI: [10.1002/andp.19003081102](https://doi.org/10.1002/andp.19003081102). [失效链接].
20. A. Akers; M. Gassman & R. Smith (2006). 《液压动力系统分析》. 纽约：泰勒与弗朗西斯. 第 13 章. ISBN 978-0-8247-9956-4.
21. A. Esposito. “通过类比简化电路分析的方法”，发表于《机械设计》，1969 年 10 月，第 173–177 页.
22. Guyton, Arthur; Hall, John (2006). 《第 14 章：循环系统概述；压力、流量和阻力的医学物理学》. 收录于 Rebecca Gruliow（编）：《医学生理学教科书》（第 11 版）. 费城, 宾夕法尼亚州：爱思唯尔公司. 第 164 页. ISBN 978-0-7216-0240-0.
23. Nilsson, James William & Riedel, Susan A. (2008). 《电路》. 普伦蒂斯-霍尔出版社. 第 29 页. ISBN 978-0-13-198925-2.
24. Halpern, Alvin M. & Erlbach, Erich (1998). 《绍姆理论与初学物理问题概要 II》. 麦格劳-希尔专业出版. 第 140 页. ISBN 978-0-07-025707-8.
25. Patrick, Dale R. & Fardo, Stephen W. (1999). 《理解直流电路》. 纽内斯出版社. 第 96 页. ISBN 978-0-7506-7110-1.
26. O'Conor Sloane, Thomas (1909). 《基础电气计算》. D. Van Nostrand Co. 第 41 页. “R = 欧姆定律的比例.”
27. Cumming, Linnaeus (1902). 《电学的实验性研究：为学校和学生使用》. 伦敦: Longman’s Green and Co. 第 220 页. “V = IR 欧姆定律.”
28. Stein, Benjamin (1997). 《建筑技术学》（第 2 版）. 约翰威立与子公司. 第 169 页. ISBN 978-0-471-59319-5.
29. Prasad, Rajendra (2006). 《电气工程基础》. 印度普伦蒂斯-霍尔出版社. ISBN 978-81-203-2729-0.
30. Hughes, E. (1969). 《电气技术》, 第 10 页, 朗文出版社.
31. Brown, Forbes T. (2006). 《工程系统动力学》. CRC 出版社. 第 43 页. ISBN 978-0-8493-9648-9.
32. Kaiser, Kenneth L. (2004). 《电磁兼容性手册》. CRC 出版社. 第 13-52 页. ISBN 978-0-8493-2087-3.
33. Horowitz, Paul; Hill, Winfield (1989). 《电子学的艺术》（第 2 版）. 剑桥大学出版社. 第 13 页. ISBN 978-0-521-37095-0.
34. Normal Lockyer, 编辑. (1876 年 9 月 21 日). “报告”. 《自然》. 第 14 卷（第 360 期）：451–459 [452]. Bibcode: [1876Natur..14..451L](https://doi.org/10.1038/014451a0). DOI: 10.1038/014451a0.
35. Kirby, C G M; Laubitz, M J (1973 年 7 月). “直流电阻测量中由珀耳帖效应引起的误差”. 《计量学》. 第 9 卷（第 3 期）：103–106. DOI: 10.1088/0026-1394/9/3/001. ISSN 0026-1394.
36. Cheremisin, M. V. (2001 年 2 月). “珀耳帖效应诱发的对欧姆电阻的修正”. 《实验与理论物理杂志》. 第 92 卷（第 2 期）：357–360. arXiv:physics/9908060. DOI: 10.1134/1.1354694. ISSN 1063-7761.
37. Lerner, Lawrence S. (1977). 《科学家与工程师的物理学》. Jones & Bartlett 出版社. 第 736 页. ISBN 978-0-7637-0460-5.
38. Seymour, J. (1972). 《物理电子学》, Pitman 出版社, 第 53-54 页.
39. Lerner, L. (1977). 《科学家与工程师的物理学》, Jones & Bartlett 出版社. 第 685-686 页.
40. Lerner, L. (1977). 《科学家与工程师的物理学》, Jones & Bartlett 出版社. 第 732-733 页.
41. Seymour J，《物理电子学》，第 48–49 页，Pitman 出版社，1972 年。

11. 进一步阅读

• 欧姆定律章节摘自《电路学习教程 第 1 卷 直流电》书籍和系列。
• John C. Shedd 和 Mayo D. Hershey，“欧姆定律的历史”，《科学流行杂志》，1913 年 12 月，第 599–614 页，Bonnier 公司，ISSN 0161-7370，介绍了欧姆的研究历史、之前的工作、欧姆在第一篇论文中的错误方程式以及欧姆实验装置的示意图。
• Schagrin, Morton L.（1963），“对欧姆定律的反抗”，《美国物理学杂志》，第 31 卷（第 7 期）：536–547，Bibcode: 1963AmJPh..31..536S，DOI: 10.1119/1.1969620，S2CID 120421759。探讨了欧姆实验工作的概念性变革。
• Kenneth L. Caneva，“欧姆，乔治·西蒙”。《科学传记大全》，2008 年。
• 《科学回忆录/2/数学研究的加尔瓦尼电路》，欧姆原始论文的翻译。

12. 外部链接

• 欧姆定律计算器