欧几里得空间（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 欧几里得空间是几何学中的基本空间，用来表示物理空间。最初在欧几里得的《几何原本》中，它指的是三维欧几里得几何空间；但在现代数学中，欧几里得空间可以是任意正整数维的空间 $n$，当需要明确维数时，称为 $n$ 维欧几里得空间。当 $n=1$ 或 $n=2$ 时，通常分别称为欧几里得直线和欧几里得平面。\(^\text{[1]}\)“欧几里得” 这一限定词用来区分欧几里得空间与后来的物理学和现代数学中研究的其他类型的空间。

　　 古希腊几何学家引入欧几里得空间来模拟物理空间。他们的工作由古希腊数学家欧几里得汇编成《几何原本》\(^\text{[2]}\)。该书的一大创新是从少数基本性质（称为公设）出发，将空间的所有性质都作为定理加以证明。这些公设有的被认为是不言自明的（例如：“通过两点可以作且仅可以作一条直线”），有的则看似无法证明（例如平行公设）。

　　 在 19 世纪末非欧几何引入之后，传统的欧几里得几何公设被重新形式化，用公理化理论来定义欧几里得空间。另一种定义方式是通过向量空间与线性代数来刻画欧几里得空间，并且已经证明这种定义与公理化定义是等价的。现代数学中更常使用这种定义，本条目中所介绍的内容也主要基于这一形式 \(^\text{[3]}\)。在所有定义中，欧几里得空间都由 “点” 组成，而这些点只通过它们在形成欧几里得空间时必须满足的性质来刻画。

　　 每个维数实际上只有一个本质上的欧几里得空间；也就是说，同一维数的所有欧几里得空间都是同构的。因此，在实际工作中，人们通常使用一个特定的欧几里得空间，记作：$\mathbf{E}^n \quad \text{或} \quad \mathbb{E}^n$,并将其用笛卡尔坐标表示为实数的 $n$ 维空间：$\mathbb{R}^n$ 并配备标准的点积结构。

1. 定义

定义的发展历史

　　 欧几里得空间最初由古希腊人提出，用来抽象化我们所处的物理空间。他们的重大创新体现在欧几里得的《几何原本》中：从少数几个抽象自物理世界的最基本性质出发，构建并证明几何学的全部内容。由于缺乏更基本的工具，这些性质无法被数学地证明，只能作为出发点，这些性质被称为公设，在现代数学语言中称为公理。这种定义欧几里得空间的方式至今仍存在，并被称为合成几何。

　　 1637 年，笛卡尔引入了笛卡尔坐标系，并展示了如何把几何问题转化为数的代数运算。这一思想把几何归约为代数，是一种重大的观念转变，因为在此之前，实数是通过长度和距离来定义的。

　　 直到 19 世纪，欧几里得几何才被扩展到三维以上的空间。路德维希·施莱夫利将欧几里得几何推广到 $n$ 维空间，结合了合成方法和代数方法，并发现了欧几里得空间中所有维度下存在的正多胞体（高维柏拉图立体的类似物）\(^\text{[4]}\)。

　　 尽管笛卡尔的解析几何方法得到广泛应用，但欧几里得空间的定义直到 19 世纪末都没有发生改变。抽象向量空间的引入使得人们能够以纯代数的方式来定义欧几里得空间。这种新的代数定义后来被证明与基于几何公理的经典定义等价，并成为现代介绍欧几里得空间时最常用的定义方式。

现代定义的动机

　　 可以把欧几里得平面看作是满足某些距离和角度关系的一组点。例如，在平面上有两类基本操作（称为 “运动”）：平移：指将整个平面沿同一个方向移动同样的距离，使所有点都发生相同的位移；旋转：指围绕平面内某个固定点旋转，使平面上的所有点都围绕该点转动同样的角度。欧几里得几何的一个基本理念是：如果一个图形可以通过一系列平移、旋转和反射变换为另一个图形，那么这两个图形应被视为全等。

　　 为了让这些概念在数学上更精确，理论必须清楚地定义什么是欧几里得空间，以及与之相关的距离、角度、平移、旋转等概念。即便在物理理论中使用，欧几里得空间仍是一种抽象，它与实际的物理位置、参考系或测量工具无关。纯数学的欧几里得空间定义同样忽略了长度单位和其他物理量的问题：在数学空间中，距离只是一个数值，而不是以英寸或米等单位表达的物理量。

　　 数学上定义欧几里得空间的标准方法（本文余下部分采用的方式）是：将其视为一个点集，其上有一个实向量空间作用，这个向量空间表示平移空间，并且配备了内积。平移的作用使得这个空间成为一个仿射空间，从而可以定义直线、平面、子空间、维数和平行性。内积则用来定义距离和角度。

　　 配备了点积的实数 $n$-元组集合 $\mathbb{R}^n$ 就是一个 $n$ 维欧几里得空间。反过来说，若在一个 $n$ 维欧几里得空间中选定一个点作为原点，并选定平移空间的一个标准正交基，则可以将该欧几里得空间与 $\mathbb{R}^n$ 建立一个同构，把它视为标准的欧几里得空间。

　　 因此，关于欧几里得空间的所有描述，同样都适用于 $\mathbb{R}^n$。正因如此，许多作者，尤其是在基础层面上，直接把 $\mathbb{R}^n$ 称作标准 $n$ 维欧几里得空间 \(^\text{[5]}\)，或简而言之称作 $n$ 维欧几里得空间。

　　 引入这种抽象定义的欧几里得空间，并使用 $\mathbb{E}^n$ 而不是 $\mathbb{R}^n$ 的一个原因是：在很多情况下，人们更倾向于以无坐标、无原点的方式进行研究（即不选择特定的基底或特定的原点）。另一个原因是：在物理世界中并不存在标准的原点或标准的基底。

技术定义

　　 欧几里得向量空间，欧几里得向量空间是一个实数域上的有限维内积空间 \(^\text{[6]}\)

　　 欧几里得空间，欧几里得空间是一个实数域上的仿射空间，并且其关联的向量空间是一个欧几里得向量空间。有时也称为欧几里得仿射空间，以区别于欧几里得向量空间 \(^\text{[6]}\)。

　　 如果 $E$ 是一个欧几里得空间，那么其关联的向量空间（欧几里得向量空间）通常记作：$\overrightarrow{E}$.欧几里得空间的维数就是其关联向量空间的维数。

　　 $E$ 的元素称为点，通常用大写字母表示。$\overrightarrow{E}$ 的元素称为**欧几里得向量或自由向量，有时也称为平移。不过严格来说，平移是指欧几里得向量作用于欧几里得空间所产生的几何变换。

　　 向量对点的作用,一个向量 $v$ 作用于一个点 $P$，会得到一个新的点，记作：$P + v$.这种作用满足： $$ P + (v + w) = (P + v) + w.~ $$ 注：左边表达式中的第二个 “+” 表示向量加法；而其他的 “+” 表示向量对点的作用。这个符号并不混淆，因为只需观察 “+” 左边的对象类型，就能判断含义。

　　 自由且传递的作用，这种作用是自由且传递的，这意味着对于任意一对点 $P, Q$，存在唯一的位移向量 $v$，使得：$P + v = Q$.这个向量 $v$ 记作：$Q - P\quad \text{或} \quad\overrightarrow{PQ}$.

　　 如前所述，欧几里得空间的一些基本性质来源于其仿射空间结构，这些内容在 “仿射结构” 及其小节中详细介绍。而由内积带来的性质，则在 “度量结构” 及其小节中加以说明。

2. 典型示例

　　 对于任意向量空间，加法在该向量空间本身上都具有自由且传递的作用。因此，欧几里得向量空间也可以看作是一个其关联向量空间就是自身的欧几里得空间。

　　 一个典型的欧几里得向量空间示例是：$\mathbb{R}^n$ 将其视为一个配备了点积作为内积的向量空间。这个特定的欧几里得空间之所以重要，是因为每一个欧几里得空间都与它同构。更准确地说，给定一个维数为 $n$ 的欧几里得空间 $E$，如果选择一个点作为原点，并在 $\overrightarrow{E}$ 中选择一个标准正交基，就可以定义一个从 $E$ 到：$\mathbb{R}^n$ 的欧几里得空间同构。

　　 由于每个 $n$ 维欧几里得空间都与 $\mathbb{R}^n$ 同构，$\mathbb{R}^n$ 有时也被称为标准 $n$ 维欧几里得空间 \(^\text{[5]}\)。

3. 仿射结构

　　 欧几里得空间的一些基本性质仅仅依赖于它是一个仿射空间这一事实。这些性质被称为仿射性质，包括直线、子空间和平行性等概念，后续小节会对此进行详细说明。

子空间

　　 设 $E$ 是一个欧几里得空间，$\overrightarrow{E}$ 是它的关联向量空间。

　　 欧几里得子空间,一个平直子空间、欧几里得子空间或仿射子空间 $F \subseteq E$ 满足： $$ \overrightarrow{F} = \bigl\{ \overrightarrow{PQ} \;\big|\; P \in F,\, Q \in F \bigr\}~ $$ 即 $F$ 的关联向量空间 $\overrightarrow{F}$ 是 $\overrightarrow{E}$ 的一个线性子空间。因此，一个欧几里得子空间 $F$ 自身也是一个欧几里得空间，其关联向量空间为 $\overrightarrow{F}$。这个线性子空间 $\overrightarrow{F}$ 也称为该子空间的方向。

　　 如果 $P$ 是 $F$ 中的一个点，则： $$ F = \bigl\{ P + v \;\big|\; v \in \overrightarrow{F} \bigr\}.~ $$ 反过来，如果 $P$ 是 $E$ 中的一个点，且 $\overrightarrow{V}$ 是 $\overrightarrow{E}$ 的一个线性子空间，则： $$ P + \overrightarrow{V} = \bigl\{ P + v \;\big|\; v \in \overrightarrow{V} \bigr\}~ $$ 是一个方向为 $\overrightarrow{V}$ 的欧几里得子空间。（该子空间的关联向量空间即为 $\overrightarrow{V}$。）

　　 如果欧几里得空间 $E$ 恰好等于它的关联向量空间 $\overrightarrow{E}$，即它是一个欧几里得向量空间，则它有两类子空间：欧几里得子空间,线性子空间;其中：所有线性子空间都是欧几里得子空间；只有包含零向量的欧几里得子空间才是线性子空间。

直线与线段

　　 在欧几里得空间中，直线是一维的欧几里得子空间。由于一维向量空间可以由任意一个非零向量生成，因此一条直线可以写作如下形式： $$ \bigl\{\, P + \lambda \overrightarrow{PQ} \;\big|\; \lambda \in \mathbb{R} \,\bigr\},~ $$ 其中 $P$ 和 $Q$ 是直线上两个不同的点。

　　 由此可知：通过两个不同的点，恰有一条直线；两条不同的直线最多有一个交点。

　　 一个更对称的表示法是： $$ \bigl\{\, O + (1-\lambda)\overrightarrow{OP} + \lambda\overrightarrow{OQ} \;\big|\; \lambda \in \mathbb{R} \,\bigr\},~ $$ 其中 $O$ 是一个任意点（不一定在直线上）。

　　 在欧几里得向量空间中，通常选择零向量作为 $O$，此时公式可简化为： $$ \bigl\{\, (1-\lambda)P + \lambda Q \;\big|\; \lambda \in \mathbb{R} \,\bigr\}.~ $$ 根据标准约定，这个公式也可以用于所有欧几里得空间（参见 “仿射空间” 章节中的仿射组合与重心部分）。

　　 线段或简称线段是连接 $P$ 和 $Q$ 的点集，对应上述公式中参数 $\lambda$ 满足 $0 \leq \lambda \leq 1$。它通常记作 $PQ$ 或 $QP$： $$ PQ = QP = \bigl\{\, P + \lambda \overrightarrow{PQ} \;\big|\; 0 \leq \lambda \leq 1 \,\bigr\}.~ $$

平行性

　　 在欧几里得空间中，如果两个维数相同的子空间 $S$ 和 $T$ 具有相同的方向（即相同的关联向量空间），则称它们是平行的 \(^\text{[a]}\)。等价地，如果存在一个平移向量 $v$，使得： $$ T = S + v,~ $$ 那么 $S$ 与 $T$ 也是平行的。

　　 对于任意一个点 $P$ 和一个子空间 $S$，存在唯一一个包含该点并且与 $S$ 平行的子空间，它可以表示为：$P + \overrightarrow{S}$.当 $S$ 是一条直线（一维子空间）时，这一性质正是普莱费尔公理的表达。

　　 因此，在一个欧几里得平面中，两条直线要么恰好有一个交点，要么互相平行。

　　 平行子空间的概念也可以推广到不同维数的子空间：如果一个子空间的方向包含在另一个子空间的方向中，那么这两个子空间也被称为平行的。

4. 度量结构

　　 与欧几里得空间 $E$ 关联的向量空间 $\overrightarrow{E}$ 是一个内积空间。这意味着存在一个对称双线性形式： $$ \begin{aligned} \overrightarrow{E} \times \overrightarrow{E} &\;\longrightarrow\; \mathbb{R} \\[6pt] (x, y) &\;\longmapsto\; \langle x, y \rangle \end{aligned}~ $$ 并且它是正定的（即当 $x \neq 0$ 时，$\langle x, x \rangle > 0$）。

　　 欧几里得空间中的内积通常称为点积，并记作 $x \cdot y$。特别是在选定笛卡尔坐标系的情况下，两个向量的内积就是它们坐标向量的点积。由于这个原因，以及历史上的沿用，点积符号比尖括号符号更常见。本文将遵循这种约定：$\langle x, y \rangle $ 记作 $x \cdot y$.

　　 向量 $x$ 的欧几里得范数为： $$ \|x\| = \sqrt{x \cdot x}.~ $$ 内积和范数使得欧几里得几何的度量性质和拓扑性质能够表达和证明。接下来的小节将介绍其中最基本的一些性质。在这些小节中：$E$ 表示一个任意的欧几里得空间；$\overrightarrow{E}$ 表示它的平移向量空间。

距离与长度

　　 在欧几里得空间中，两点之间的距离（更准确地说是欧几里得距离）是把一个点平移到另一个点的平移向量的范数。即： $$ d(P, Q) = \bigl\| \overrightarrow{PQ} \bigr\|.~ $$ 线段 $PQ$ 的长度就是其端点 $P$ 和 $Q$ 之间的距离 $d(P, Q)$，通常记作：$|PQ|$.

　　 这种距离是一个度量，因为它满足：正定性：$d(P, Q) \ge 0$，且 $d(P, Q) = 0$ 当且仅当 $P = Q$；对称性：$d(P, Q) = d(Q, P)$；三角不等式： $$ d(P, Q) \le d(P, R) + d(R, Q).~ $$ 当且仅当点 $R$ 位于线段 $PQ$ 上时，上式中的等号成立。这说明：三角形任一边的长度小于或等于其他两边长度之和。这正是 “三角不等式” 这一名称的来源。

　　 有了欧几里得距离后，每个欧几里得空间都是一个完备的度量空间。

正交性

　　 在欧几里得空间 $E$ 的关联向量空间 $\overrightarrow{E}$ 中，若两个非零向量 $u$ 和 $v$ 的内积为零，则它们是正交或垂直的： $$ u \cdot v = 0~ $$ 如果两个线性子空间的任意一个非零向量都与另一个子空间的所有非零向量正交，那么这两个线性子空间是正交的。这意味着它们的交集仅包含零向量。

　　 两条直线，或者更一般地说，两个欧几里得子空间，如果它们的方向向量空间彼此正交，则称它们是正交的。特别地，若两条正交直线相交，则称它们是垂直的。

　　 两条共享公共端点的线段 $AB$ 和 $AC$ 是垂直的（或称形成直角），当且仅当向量 $\overrightarrow{AB}$ 和 $\overrightarrow{AC}$ 正交。

　　 如果 $AB$ 和 $AC$ 形成直角，则有： $$ |BC|^2 = |AB|^2 + |AC|^2.~ $$ 这就是勾股定理。在这种向量和内积的框架下，证明这一结果非常直接：利用内积的双线性性和对称性，可以写为： $$ \begin{aligned} |BC|^2 &= \overrightarrow{BC} \cdot \overrightarrow{BC} \\[4pt] &= (\overrightarrow{BA} + \overrightarrow{AC}) \cdot (\overrightarrow{BA} + \overrightarrow{AC}) \\[4pt] &= \overrightarrow{BA} \cdot \overrightarrow{BA} + \overrightarrow{AC} \cdot \overrightarrow{AC} - 2 \overrightarrow{AB} \cdot \overrightarrow{AC} \\[4pt] &= \overrightarrow{AB} \cdot \overrightarrow{AB} + \overrightarrow{AC} \cdot \overrightarrow{AC} \\[4pt] &= |AB|^2 + |AC|^2. \end{aligned}~ $$ 其中，使用了条件：$\overrightarrow{AB} \cdot \overrightarrow{AC} = 0$ 因为这两个向量是正交的。

角

　　 在欧几里得空间 $E$ 的关联向量空间 $\overrightarrow{E}$ 中，两个非零向量 $x$ 和 $y$ 之间的（无向）夹角 $\theta$ 定义为：

　　 $$ \theta = \arccos\!\left(\frac{x \cdot y}{|x|\,|y|}\right),~ $$

　　 其中 $\arccos$ 表示反余弦函数的主值。根据柯西–施瓦兹不等式，反余弦函数的自变量总在区间 $[-1, 1]$ 内。因此，$\theta$ 是实数，且范围为：$0 \leq \theta \leq \pi$（若用角度制表示，则是 $0 \leq \theta \leq 180^\circ$）。

　　 在欧几里得直线上，角度没有意义，因为角度只能取 $0$ 或 $\pi$。

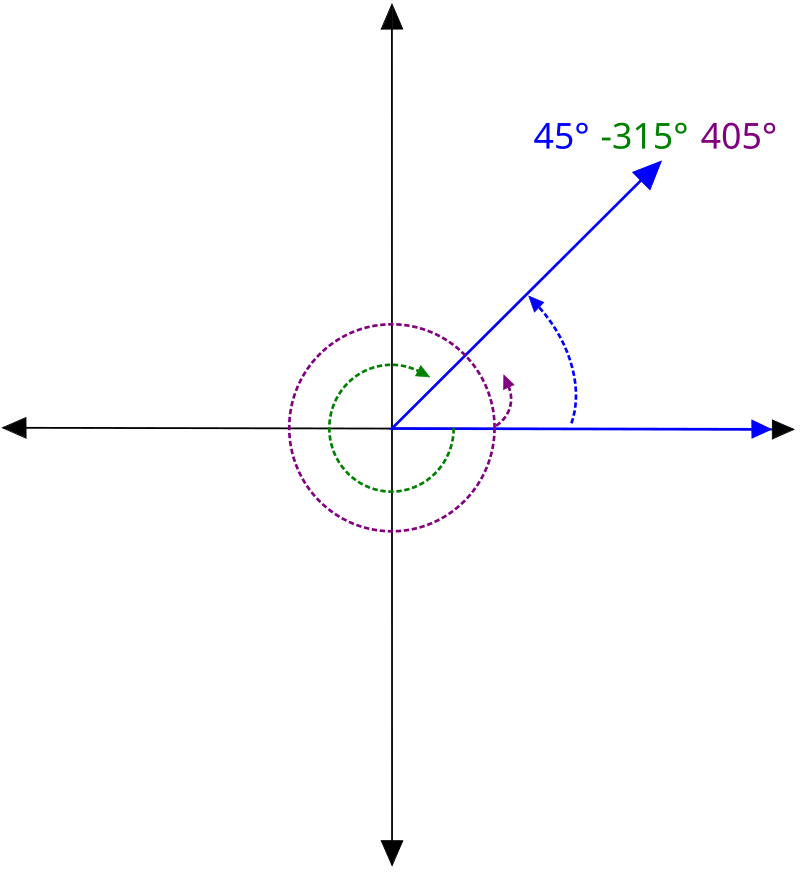
　　 在有向欧几里得平面中，可以定义两个向量的有向夹角。此时，向量 $x$ 与 $y$ 的有向夹角是向量 $y$ 与 $x$ 的有向夹角的相反数。这种情况下，夹角可以取任意值（模 $2\pi$ 的整数倍）。特别地，当夹角满足：$\pi < \theta < 2\pi$ 时，可以等价地看作负角度：$-\pi < \theta - 2\pi < 0$。

　　 两个向量的夹角在它们分别被正数缩放时不会发生改变。更确切地说，如果 $x$ 和 $y$ 是两个向量，$\lambda$ 和 $\mu$ 是实数，则有： $$ \operatorname{angle}(\lambda x, \mu y) = \begin{cases} \operatorname{angle}(x, y), & \text{如果 } \lambda \text{ 和 } \mu \text{ 同号；} \\[6pt] \pi - \operatorname{angle}(x, y), & \text{否则。} \end{cases}~ $$ 如果 $A$、$B$、$C$ 是欧几里得空间中的三点，则线段 $AB$ 和 $AC$ 的夹角就是向量 $\overrightarrow{AB} \quad \text{与} \quad \overrightarrow{AC}$ 的夹角。由于向量乘以正数不会改变夹角，因此可以定义以 $A$ 为起点的两条半直线的夹角：它就是任意取两点 $B$ 和 $C$（分别位于两条半直线上）所构成的线段 $AB$ 和 $AC$ 的夹角。尽管这种用法较少见，但同样可以推广定义不共享起点的线段或半直线的夹角。

　　 两条直线的夹角定义如下：若某两条线段（分别在两条直线上）的夹角为 $\theta$，则选择这两条直线上任意其他两条线段，其夹角要么是 $\theta$，要么是 $\pi - \theta$。其中，一个夹角位于区间：$[0, \pi/2]$ 另一个位于：$[\pi/2, \pi]$ 两条直线的无向夹角指位于区间 $[0, \pi/2]$ 的那个角。在有向欧几里得平面**中，两条直线的有向夹角属于区间：$[-\pi/2, \pi/2]$.

笛卡尔坐标

　　 每一个欧几里得向量空间都有一个正交归一基（在一维空间中有两个，在高于一维的空间中有无穷多个）。所谓正交归一基 $(e_1, \dots, e_n)$ 是由满足以下条件的基向量组成的：每个向量都是单位向量：$\|e_i\| = 1$ 向量之间两两正交：$e_i \cdot e_j = 0 \quad (i \ne j)$ 更具体地说，给定任意一个基 $(b_1, \dots, b_n)$，通过**Gram–Schmidt 正交化过程**可以构造出一个正交归一基，使得对于每个 $i$，$(e_1, \dots, e_i)$ 和 $(b_1, \dots, b_i)$ 所生成的线性子空间相同[7]。

　　 对于一个欧几里得空间 $E$，一个笛卡尔框架由以下两部分组成：其关联向量空间 $\overrightarrow{E}$ 的一个正交归一基；空间 $E$ 中的一个点，称为原点，通常记作 $O$。一个笛卡尔框架：$(O, e_1, \dots, e_n)$ 允许为 $E$ 和 $\overrightarrow{E}$ 定义笛卡尔坐标，具体如下：

　　 向量的笛卡尔坐标,向量 $v \in \overrightarrow{E}$ 的笛卡尔坐标是 $v$ 在正交归一基 $e_1, \dots, e_n$ 下的系数。

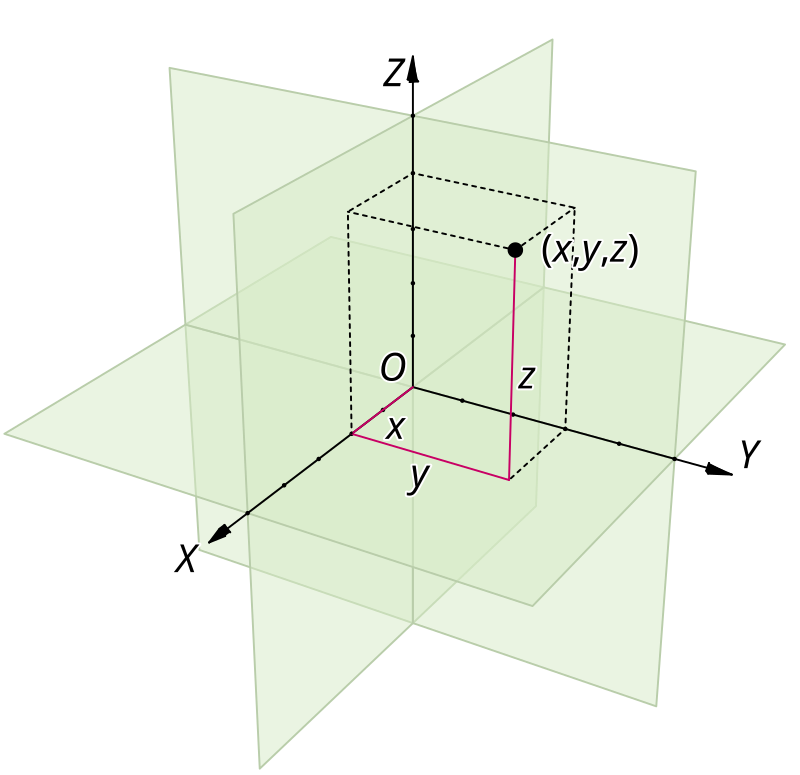
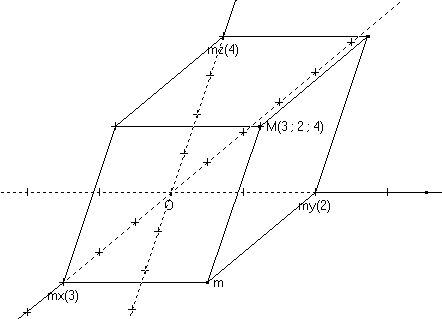
　　 例如，在三维欧几里得空间中，如果正交归一基为 $(e_1, e_2, e_3)$，可以习惯性地称它们为 $(x, y, z)$ 方向，那么向量：$v = \alpha_1 e_1 + \alpha_2 e_2 + \alpha_3 e_3$ 的笛卡尔坐标就是：$(\alpha_1, \alpha_2, \alpha_3)$.由于基是正交归一的，第 $i$ 个坐标 $\alpha_i$ 等于：$\alpha_i = v \cdot e_i$.

　　 点的笛卡尔坐标,空间 $E$ 中某点 $P$ 的笛卡尔坐标就是向量：$\overrightarrow{OP}$ 的笛卡尔坐标。

其他坐标系

　　 由于欧几里得空间是一个仿射空间，我们可以在其上考虑仿射框架。仿射框架与欧几里得框架类似，但基向量不要求是正交归一的。这会生成仿射坐标，有时也称为斜坐标，以强调基向量并非两两正交。

　　 在一个维数为 $n$ 的欧几里得空间中，仿射基是指不共面的 $n+1$ 个点。仿射基可以为空间中的每个点定义重心坐标。

　　 在一个维数为 $n$ 的欧几里得空间 $E$ 中，可以用如下方式定义许多其他的坐标系：设 $f$ 是从 $E$ 的一个稠密开子集映射到 $\mathbb{R}^n$ 的一个同胚（或更常见的是微分同胚）。那么，对于 $E$ 中的一个点 $x$，其坐标就是 $f(x)$ 的各个分量。极坐标系适用于二维空间；球坐标系和圆柱坐标系适用于三维空间；这些都是通过这种方式定义的。

　　 对于那些不在 $f$ 定义域中的点，有时可以通过邻近点的坐标极限来定义其坐标，但这类坐标可能不唯一，并且在该点附近不连续。例如，在球坐标系中：极点处的经度是未定义的；在反子午线上，经度会从 $-180^\circ$ 跳跃到 $+180^\circ$。

　　 这种定义坐标的方法可以很容易地推广到其他数学结构，尤其是推广到流形的研究中。

5. 等距映射

　　 在两个度量空间之间，等距映射是一个保持距离的双射映射，\(^\text{[b]}\) 即： $$ d(f(x), f(y)) = d(x, y)~ $$ 在欧几里得向量空间的情形下，如果一个等距映射把原点映射到原点，那么它会保持向量的范数： $$ \|f(x)\| = \|x\|~ $$ 因为向量的范数就是它与零向量的距离。它同样保持向量的内积： $$ f(x) \cdot f(y) = x \cdot y~ $$ 这是因为： $$ x \cdot y = \tfrac{1}{2} \big(\|x + y\|^2 - \|x\|^2 - \|y\|^2\big)~ $$ 因此，欧几里得向量空间上的等距映射一定是一个线性同构 \(^\text{[c][8]}\)。

　　 一个欧几里得空间之间的等距映射 $f: E \to F$ 会在它们对应的欧几里得向量空间之间诱导一个等距映射：$\overrightarrow{f}: \overrightarrow{E}\to \overrightarrow{F}$.这意味着，两个等距的欧几里得空间具有相同的维数。反过来，如果 $E$ 和 $F$ 是欧几里得空间，且 $O \in E$、$O' \in F$，并且 $\overrightarrow{f}: \overrightarrow{E} \to \overrightarrow{F}$ 是一个等距映射，那么定义： $$ f(P) = O' + \overrightarrow{f}(\overrightarrow{OP})~ $$ 就得到一个欧几里得空间的等距映射。

　　 根据上述结果，欧几里得空间的等距映射具备以下性质：把直线映射到直线；更一般地，把欧几里得子空间映射到相同维数的欧几里得子空间；并且这些子空间上的限制映射也是该子空间的等距映射。

等距映射的典型示例

　　 若 $E$ 是一个欧几里得空间，它的关联向量空间 $\overrightarrow{E}$ 也可以看作一个欧几里得空间。每个点 $O \in E$ 都定义了一个欧几里得空间的等距映射： $$ P \;\mapsto\; \overrightarrow{OP}~ $$ 它将点 $O$ 映射到零向量，且其关联的线性映射是恒等映射。其逆映射为： $$ v \;\mapsto\; O + v~ $$ 一个欧几里得框架 $(O, e_1, \dots, e_n)$ 可以定义如下映射： $$ \begin{aligned} E &\;\to\; \mathbb{R}^n \\ P &\;\mapsto\; \bigl( e_1 \cdot \overrightarrow{OP}, \; \dots, \; e_n \cdot \overrightarrow{OP} \bigr), \end{aligned}~ $$ 这是一个欧几里得空间的等距映射。其逆映射为： $$ \begin{aligned} \mathbb{R}^n &\;\to\; E \\ (x_1, \dots, x_n) &\;\mapsto\; O + x_1 e_1 + \dots + x_n e_n \end{aligned}~ $$ 这意味着：在同构意义下，任意一个给定维数的欧几里得空间都是唯一的。

　　 因此，许多作者会直接把：$\mathbb{R}^n$ 称为 $n$ 维欧几里得空间。

欧几里得群

　　 一个从欧几里得空间映射到其自身的等距映射称为欧几里得等距、欧几里得变换或刚体变换。欧几里得空间的所有刚体变换在复合运算下构成一个群，称为欧几里得群，通常记作：$E(n)$.

　　 最简单的欧几里得变换是平移： $$ P \;\to\; P + v~ $$ 这些平移与向量是一一对应的。这也是为什么把平移空间称为欧几里得空间的关联向量空间的原因。平移组成了欧几里得群的一个正规子群。

　　 一个欧几里得空间 $E$ 的欧几里得等距映射 $f$ 可以定义其关联向量空间的一个线性等距映射 $\overrightarrow{f}$（线性等距映射指既是等距映射又是线性映射），具体如下：记 $P Q$ 的向量为：$Q - P = \overrightarrow{PQ}$,若 $O$ 是 $E$ 中的任意一点，则有： $$ \overrightarrow{f}(\overrightarrow{OP}) = f(P) - f(O)~ $$ 很容易证明，这个映射是一个与选择的点 $O$ 无关的线性映射。

　　 映射：$f \;\longmapsto\; \overrightarrow{f}$ 是一个从欧几里得群到线性等距群的群同态。该同态的核是平移群，这表明平移群是欧几里得群的一个正规子群。

　　 所有固定某个点 $P$ 的等距映射构成欧几里得群关于点 $P$ 的稳定子群。这个稳定子群在上述群同态的限制下，与正交群同构。因此，固定某个点的等距映射形成一个与正交群同构的群。

　　 设 $P$ 是欧几里得空间中的一个点，$f$ 是一个等距映射，$t$ 是把 $P$ 映射到 $f(P)$ 的平移。定义：$g = t^{-1} \circ f$,则 $g$ 固定点 $P$。于是可以写出：$ f = t \circ g$,这说明欧几里得群是平移群与正交群的半直积。

　　 特殊正交群是正交群的一个正规子群，负责保持空间的手性。它是正交群的一个指数为 2 的子群。通过同态：$f \;\mapsto\; \overrightarrow{f}$,它的逆像是欧几里得群的一个指数为 2 的正规子群，称为特殊欧几里得群或位移群。该群的元素称为刚体运动或位移。

　　 刚体运动包括：恒等变换；平移；旋转（至少固定一个点的刚体运动）；螺旋运动。一些不是刚体运动的刚体变换包括：反射：这类刚体变换固定一个超平面，但不是恒等映射； 在某个欧几里得坐标系下，将某一坐标符号改变的变换。由于特殊欧几里得群是欧几里得群的一个指数为 2 的子群，对于任何一个反射 $r$，所有不是刚体运动的刚体变换都可以表示为：$r \circ$ 某个刚体运动滑动反射就是一个既不是刚体运动也不是单纯反射的刚体变换实例。

　　 本节中涉及的所有群，包括欧几里得群、特殊欧几里得群和正交群，都是李群和代数群。

6. 拓扑

　　 欧几里得距离使欧几里得空间成为一个度量空间，因此它也是一个拓扑空间。这种拓扑被称为欧几里得拓扑。对于 $\mathbb{R}^n$ 来说，这个拓扑也就是积拓扑。

　　 开集指的是：对于其中的每一个点，都包含一个该点为中心的开球。换句话说，开球的集合构成了拓扑的一个基。

　　 欧几里得空间的拓扑维数等于它的几何维数。这意味着不同维数的欧几里得空间不是同胚的。此外，领域不变性定理断言：欧几里得空间的一个子集（在子空间拓扑下）是开集，当且仅当它同胚于某个相同维数的欧几里得空间中的开子集。

　　 欧几里得空间是完备的，同时也是局部紧致的。也就是说，一个欧几里得空间的闭子集是紧致的，当且仅当它是有界的（即包含在某个球内）。特别地，闭球是紧致的。

7. 公理化定义

　　 本文所描述的欧几里得空间的定义，与欧几里得本人给出的定义有着根本的不同。实际上，欧几里得并没有正式地定义空间，因为在当时，空间被视为独立于人类思维存在的物理世界的描述。直到 19 世纪末，随着非欧几何的出现，人们才意识到需要对欧几里得空间给出严格的形式化定义。

　　 形成了两种不同的研究途径：克莱因提出通过研究几何的对称群来定义几何。本文所介绍的欧几里得空间的定义，本质上源自他的埃尔兰根纲领，着重强调平移群和等距群的结构。希尔伯特提出了一套受欧几里得公设启发的公理体系。类体系属于合成几何，因为它们不涉及实数的定义。后来，G. D. Birkhoff 和 Alfred Tarski 提出了更简化的公理体系，这些体系直接引入实数（参见 Birkhoff 公理 和 Tarski 公理）。

　　 在几何代数的框架下，Emil Artin 证明了所有这些欧几里得空间的定义是等价的**\(^\text{[9]}\)。事实上，可以比较容易地证明：所有欧几里得空间的定义都满足希尔伯特公理；所有涉及实数的定义（包括本文的定义）都是等价的。

　　 Artin 证明中最困难的部分在于以下问题：在希尔伯特公理中，全等关系是线段上的一个等价关系，因此可以把线段的长度定义为它的等价类。为了完成证明，必须说明这种 “长度” 满足非负实数所具有的性质。Artin 利用与希尔伯特公理等价的一组公理，成功地完成了这一证明。

应用

　　 自古希腊以来，欧几里得空间就被用于物理世界形状的建模。因此，它被广泛应用于许多科学领域，如物理学、力学、天文学等。它也广泛用于所有与形状、图形、位置和方位相关的技术领域，例如建筑学、大地测量学、地形学、导航、工业设计、工程制图等。

　　 在现代物理学的许多理论中，三维以上的空间也会出现（参见高维空间）。它们同样出现在物理系统的构型空间中。

　　 除了欧几里得几何，欧几里得空间还广泛用于数学的其他领域：可微流形的切空间是欧几里得向量空间；更一般地说，流形是一个局部可以用欧几里得空间近似的空间；大多数非欧几何都可以建模为流形，并嵌入到更高维的欧几里得空间中。例如，椭圆空间可以用椭球面来建模。此外，数学中有许多对象本身并不具备几何性质，但通常也会用欧几里得空间来表示，例如图论中的图的常见可视化表示。

8. 其他几何空间

　　 自 19 世纪末引入非欧几何以来，人们研究了许多可以像欧几里得空间那样进行几何推理的空间。这些空间通常与欧几里得空间共享一些性质，但也可能拥有一些看似奇特的属性。其中有些空间的定义依赖于欧几里得几何，或者可以建模为高维欧几里得空间的子空间。当一个空间通过几何公理来定义时，将它嵌入欧几里得空间是一种常见方法，用于证明该空间定义的一致性。更准确地说，这是在假定欧几里得几何一致的前提下，证明其理论一致性（虽然欧几里得几何本身的一致性是无法严格证明的）。

仿射空间

　　 欧几里得空间可以看作是一个配备了度量的仿射空间。而仿射空间在数学中有许多其他应用。特别是，由于仿射空间可以定义在任意域上，它使得几何学能够在不同的背景下进行推广。

　　 当涉及非线性问题时，通常会考虑在复数域上的仿射空间，把它作为欧几里得空间的扩展。例如，在复数仿射空间中，一条直线和一个圆总有两个交点（这两个点可能重合）。因此，大部分代数几何都是建立在复数仿射空间或代数闭域上的仿射空间中的。在这些空间中研究的对象称为仿射代数簇。

　　 定义在有理数域或更一般的代数数域上的仿射空间，则在（代数）几何与数论之间建立了联系。例如，费马大定理可以表述为：“次数大于 2 的费马曲线在有理数仿射平面上没有点。”

　　 定义在有限域上的仿射空间中的几何也被广泛研究。例如，有限域上的椭圆曲线被广泛应用于密码学。

射影空间

　　 最初，引入射影空间的动机是在欧几里得空间（更广义地说是仿射空间）中添加 “无穷远点”，以使以下命题成立：“两条共面的直线必然相交于唯一的一点。” 射影空间与欧几里得空间、仿射空间共享一个特性：各向同性，即空间中没有任何固有属性可以区分两点或两条直线。因此，现在更常用的一种更各向同性的定义是：射影空间是某个维数高一维的向量空间中的所有向量直线的集合。

　　 和仿射空间类似，射影空间也可以定义在任意域上，并且是代数几何中的基本空间之一。

非欧几何

　　 非欧几何通常指的是平行公理不成立的几何空间。它们包括：椭圆几何：三角形内角和大于 $180^\circ$；双曲几何：三角形内角和小于 $180^\circ$。这些几何在 19 世纪下半叶被提出，且通过证明其理论的一致性（假设欧几里得几何无矛盾）而被数学界接受。这种发展也直接导致了 20 世纪初数学基础危机的出现，并推动了数学公理化理论的系统化。

射影空间

　　 最初，引入射影空间的动机是在欧几里得空间（更广义地说是仿射空间）中添加 “无穷远点”，以使以下命题成立：“两条共面的直线必然相交于唯一的一点。” 射影空间与欧几里得空间、仿射空间共享一个特性：各向同性，即空间中没有任何固有属性可以区分两点或两条直线。因此，现在更常用的一种更各向同性的定义是：射影空间是某个维数高一维的向量空间中的所有向量直线的集合。

　　 和仿射空间类似，射影空间也可以定义在任意域上，并且是代数几何中的基本空间之一。

非欧几何

　　 非欧几何通常指的是平行公理不成立的几何空间。它们包括：椭圆几何：三角形内角和大于 $180^\circ$；双曲几何：三角形内角和小于 $180^\circ$。这些几何在 19 世纪下半叶**被提出，且通过证明其理论的一致性（假设欧几里得几何无矛盾）而被数学界接受。这种发展也直接导致了 20 世纪初数学基础危机 的出现，并推动了数学公理化理论的系统化。

曲空间

　　 流形是一类在每个点的邻域内都与欧几里得空间相似的空间。更严格地说，流形是一个拓扑空间，其中每个点都有一个邻域同胚于某个欧几里得空间的开子集。根据这种 “相似程度” 的不同，流形可以进一步分类为：拓扑流形,可微流形,光滑流形,解析流形然而，这些 “相似性” 都不涉及距离或角度，即便是近似的也没有。

　　 在光滑流形上，可以通过在每个点的切空间上赋予一个平滑变化的欧几里得度量（切空间本身是欧几里得向量空间）来定义距离和角度。这样得到的空间称为黎曼流形。在黎曼流形中：一般不存在严格意义上的 “直线”，但有类似直线的对象——测地线，它们是两点之间的 “最短路径”；距离通过沿测地线的长度来定义；两条测地线的夹角则由它们在交点处切空间中的切向量夹角决定。因此，黎曼流形可以看作一种 “局部弯曲的欧几里得空间”。

　　 欧几里得空间显然是最简单的黎曼流形。一个形象的例子是球面：在球面上，测地线是大圆弧；在导航学中，这些大圆弧又称为正航线。更一般地说，许多非欧几何空间都可以通过黎曼流形的形式来实现。

伪欧几里得空间

　　 一个实向量空间的内积是一种正定双线性形式，因此它由一个正定二次型刻画。而*伪欧几里得空间则是指：其关联实向量空间上配备了一个非退化但可能是不定的二次型的仿射空间。

　　 这种空间的一个基本例子是闵可夫斯基空间，它是爱因斯坦狭义相对论中的时空模型。闵可夫斯基空间是一个四维空间，其度量由以下二次型定义： $$ x^2 + y^2 + z^2 - t^2,~ $$ 其中：最后一项 $t$ 表示时间坐标；其他三项 $x, y, z$ 表示空间坐标。

　　 为了将引力效应纳入考虑，广义相对论使用的是一种伪黎曼流形，其每个点的切空间都是一个闵可夫斯基空间。在这种模型中，流形在某点的曲率取决于该点处引力场的大小。

9. 参见

• 希尔伯特空间：一种推广到无限维的空间，广泛应用于泛函分析
• 位置空间：物理学中的一种应用

10. 脚注

　　
a.某个子空间是否被认为与自身平行，可能取决于具体上下文或作者的约定。
b.如果去掉 “双射” 的条件，一个保持距离的函数必然是单射的，并且它是从其定义域到其像的一个等距映射。
c.证明：需要证明 $f(\lambda x + \mu y) - \lambda f(x) - \mu f(y) = 0$.为此，只需证明左边向量的范数平方为零即可。利用内积的双线性性质，这个范数平方可以展开为：$\|f(x)\|^2, \quad \|f(y)\|^2, \quad f(x) \cdot f(y)$ 的线性组合。由于 $f$ 是等距映射，这些项可以分别用：$\|x\|^2, \quad \|y\|^2, \quad x \cdot y$ 来替换，从而化简得到结果为零。

11. 参考文献

1. Solomentsev 2001.
2. Ball 1960, 第 50–62 页.
3. Berger 1987.
4. Coxeter 1973.
5. Berger 1987, 第 9.1 节.
6. Berger 1987, 第 9 章.
7. Anton (1987, 第 209–215 页).
8. Berger 1987, 命题 9.1.3.
9. Artin 1988.

• Anton, Howard (1987). Elementary Linear Algebra (第 5 版). 纽约: Wiley. ISBN 0-471-84819-0.
• Artin, Emil (1988) [1957]. Geometric Algebra. Wiley Classics Library. 纽约: John Wiley & Sons Inc. 页码: x+214. doi:10.1002/9781118164518. ISBN 0-471-60839-4. MR 1009557.
• Ball, W\.W. Rouse (1960) [1908]. A Short Account of the History of Mathematics (第 4 版). Dover Publications. ISBN 0-486-20630-0.
• Berger, Marcel (1987). Geometry I. 柏林: Springer. ISBN 3-540-11658-3.
• Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (第 3 版). 纽约: Dover.（Schläfli 在 1853 年前就发现了这些多胞体——那时，Cayley、Grassmann 和 Möbius 是仅有的几个曾设想三维以上几何可能性的人。）
• Solomentsev, E.D. (2001) [1994]. “Euclidean space”. Encyclopedia of Mathematics. EMS Press.