纳维-斯托克斯方程（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 纳维–斯托克斯方程（/nævˈjeɪ stoʊks/，音译为 “纳维-耶 斯托克斯”）是一组描述黏性流体运动的偏微分方程。这些方程以法国工程师兼物理学家克洛德–路易·纳维和爱尔兰物理学家、数学家乔治·加布里埃尔·斯托克斯的名字命名。它们的理论是在数十年的发展过程中逐步建立起来的，从 1822 年（纳维的工作）到 1842–1850 年（斯托克斯的研究）。

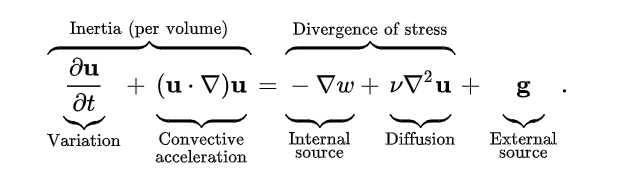
　　 纳维–斯托克斯方程在数学上表达了牛顿流体的动量平衡，并结合了质量守恒原理。有时，这些方程会配合状态方程一起使用，用来联系压力、温度和密度 $1$。它们的推导源于将牛顿第二定律应用于流体运动，并假设流体中的应力可以分解为扩散型的黏性项（与速度梯度成正比）和压力项，从而描述黏性流动。与密切相关的欧拉方程相比，纳维–斯托克斯方程考虑了黏性，而欧拉方程仅适用于无黏性流动。正因为如此，纳维–斯托克斯方程属于椭圆型方程，因此具备更好的解析性质，但代价是数学结构较少（例如，它们从不完全可积）。

　　 纳维–斯托克斯方程非常有用，因为它们描述了许多科学和工程领域中感兴趣现象的物理规律。它们可以用来模拟天气、洋流、管道中的水流以及机翼周围的空气流动。在完整形式或简化形式下，纳维–斯托克斯方程都能帮助进行飞机和汽车的设计、研究血液流动、设计发电站、分析污染问题，以及解决许多其他复杂问题。如果将其与麦克斯韦方程组耦合，还可以用于模拟和研究磁流体力学现象。

　　 从纯数学角度来看，纳维–斯托克斯方程同样具有极高的研究价值。尽管它们有着广泛的实际应用，但至今尚未被证明三维情况下的光滑解是否总是存在——也就是说，解在定义域的所有点上是否无限可微（甚至只是有界）仍是一个未解的问题。这被称为 “纳维–斯托克斯方程的存在性与光滑性问题”。克雷数学研究所将其列为数学界七大未解难题之一，并悬赏 100 万美元奖励对该问题的证明或反例 \(^\text{[2][3]}\)。

1. 流速

　　 纳维–斯托克斯方程的解是流速。它是一个矢量场——在某段时间区间的任意时刻，方程为流体中每一个空间点给出一个矢量，这个矢量的方向和大小对应于该点在该时刻的流体速度。研究对象通常是三维空间加一维时间，而在纯数学和应用数学中，也会研究更高维的类似情况。

　　 一旦计算出了速度场，就可以通过动力学方程或相关关系推导出其他感兴趣的物理量，例如压力或温度。这与经典力学的常见情况不同，经典力学的解通常是单个粒子的轨迹或连续介质的偏移轨迹。而对于流体而言，研究速度场比研究位置更有意义。不过，为了可视化分析，人们仍然可以计算不同的轨迹。

　　 特别是，当速度场被看作一个矢量场时，它的流线可以理解为 “无质量流体粒子” 会沿着运动的路径。这些路径就是积分曲线，它们在每一点的切向导数等于该点的速度矢量，可以直观地展示矢量场在某一时刻的整体流动行为。

2. 广义连续介质方程

　　 纳维–斯托克斯动量方程可以看作是柯西动量方程的一种特例，其广义对流形式为： $$ \frac{\mathrm{D} \mathbf{u}}{\mathrm{D} t} = \frac{1}{\rho} \nabla \cdot \boldsymbol{\sigma} + \mathbf{f}.~ $$ 其中：$\mathbf{u}$ 表示流体速度矢量；$\rho$ 是流体密度；$\boldsymbol{\sigma}$ 是柯西应力张量；$\mathbf{f}$ 是单位质量上的外力，例如重力或电磁力。

　　 如果将柯西应力张量 $\boldsymbol{\sigma}$ 设为黏性应力项 $\boldsymbol{\tau}$（偏应力，deviatoric stress）和压力项 $-p\mathbf{I}$（体积应力，volumetric stress）的和，即： $$ \boldsymbol{\sigma} = \boldsymbol{\tau} - p\mathbf{I},~ $$ 则可以得到柯西动量方程的对流形式： $$ \rho \frac{\mathrm{D} \mathbf{u}}{\mathrm{D} t} = -\nabla p + \nabla \cdot \boldsymbol{\tau} + \rho \,\mathbf{a}.~ $$ 其中：

　　 由此形式可以明显看出，如果假设流体是无黏性流体，即没有偏应力项 $\boldsymbol{\tau}$，那么柯西动量方程就会简化为欧拉方程。

　　 假设质量守恒，并结合散度与梯度的已知性质，可以使用质量连续性方程来表示均质流体在空间与时间上的单位体积质量（即密度 $\rho$）随物质导数 $\displaystyle \frac{\mathbf{D}}{\mathbf{Dt}}$ 的变化，用以刻画流体介质中速度变化的关系： $$ \frac{\mathbf{D} m}{\mathbf{D} t} = \iiint\limits_{V} \left( \frac{\mathbf{D} \rho}{\mathbf{D} t} + \rho \, (\nabla \cdot \mathbf{u}) \right) \, dV~ $$ 进一步可得： $$ \frac{\mathbf{D} \rho}{\mathbf{D} t} + \rho (\nabla \cdot \mathbf{u}) = \frac{\partial \rho}{\partial t} + (\nabla \rho) \cdot \mathbf{u} + \rho (\nabla \cdot \mathbf{u}) = \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0~ $$ 其中：

　　 注 1：算符 $\nabla$（nabla 符号）表示数学运算符 del，用于表示梯度、散度和旋度等向量分析操作。

　　 这一过程最终得到守恒形式的柯西动量方程，常写作 \(^\text{[4]}\)： $$ \frac{\partial}{\partial t}(\rho \mathbf{u}) + \nabla \cdot (\rho \mathbf{u} \otimes \mathbf{u}) = -\nabla p + \nabla \cdot \boldsymbol{\tau} + \rho \mathbf{a}~ $$ 其中，符号 $\otimes$ 表示流速 $\mathbf{u}$ 的外积：

　　 $$ \mathbf{u} \otimes \mathbf{u} = \mathbf{u} \mathbf{u}^\mathrm{T}.~ $$

　　 公式解析：

　　 方程左边描述了加速度，由时间依赖项和对流项组成（如果是在非惯性参考系下，还包括非惯性效应）；方程右边可以看作三部分的合力：静水压力项（$-\nabla p$）；偏应力（黏性应力）的散度项（$\nabla \cdot \boldsymbol{\tau}$）；体力项（$\rho \mathbf{a}$，如重力等）。

　　 所有非相对论性的平衡方程（包括纳维–斯托克斯方程）都可以通过柯西动量方程出发，结合本构关系来得到。当将偏应力张量用黏度和流速梯度来表示，并假设黏度为常数时，上述柯西方程就会导出后续的纳维–斯托克斯方程。

3. 对流加速度

　　 柯西方程以及由其推导出的所有连续介质方程（包括欧拉方程和纳维–斯托克斯方程）的一个显著特征是对流加速度：即流动相对于空间位置产生的加速度效应。虽然单个流体微粒确实会经历随时间变化的加速度，但流场的对流加速度是一种空间效应，例如流体在喷嘴中被加速就是一个典型的例子。

图
图 1：一个对流的例子：即使流动是稳态的（与时间无关），当流体沿着扩张的管道向下流动时（假设是不可压缩流或亚音速可压缩流），流体速度会逐渐减小，因此在空间位置上仍然存在加速度效应。

4. 可压缩流

　　 说明：这里的偏应力张量依然记作 $\boldsymbol{\tau}$，与广义连续介质方程以及不可压缩流部分的表示一致。

　　 可压缩流动的动量纳维–斯托克斯方程是基于以下关于柯西应力张量的假设推导出来的 \(^\text{[5]}\)：

　　 其中：$\mathbf{I}$ 表示恒等张量；$\operatorname{tr}(\boldsymbol{\varepsilon})$ 表示应变率张量的迹。

　　 因此，应力张量可以显式写为： $$ \boldsymbol{\sigma} = -p\mathbf{I} + \lambda (\nabla \cdot \mathbf{u}) \mathbf{I} + \mu \left(\nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}}\right).~ $$ 由于在三维空间中，应变率张量的迹就是**流动的散度**（即流体的膨胀速率）： $$ \operatorname{tr}(\boldsymbol{\varepsilon}) = \nabla \cdot \mathbf{u}.~ $$ 并且在三维空间中，恒等张量的迹为： $$ \operatorname{tr}(\mathbf{I}) = 3.~ $$ 因此，在三维空间中，应力张量的迹为： $$ \operatorname{tr}(\boldsymbol{\sigma}) = -3p + (3\lambda + 2\mu)\nabla \cdot \mathbf{u}.~ $$ 所以，通过将应力张量分解为各向同性部分和偏应力部分（这是流体力学中的常规做法 \(^\text{[6]}\)），可以写为： $$ \boldsymbol{\sigma} = -\left[ p - \left(\lambda + \tfrac{2}{3}\mu\right)(\nabla \cdot \mathbf{u}) \right]\mathbf{I} + \mu \left( \nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} - \tfrac{2}{3}(\nabla \cdot \mathbf{u})\mathbf{I} \right).~ $$ 引入体黏度 $\zeta$： $$ \zeta \equiv \lambda + \tfrac{2}{3}\mu.~ $$ 我们最终得到热流体力学中常用的线性本构方程 \(^\text{[5]}\)：

　　 流体的线性应力本构方程 $$ \boldsymbol{\sigma} = -\big[p - \zeta (\nabla \cdot \mathbf{u})\big]\mathbf{I} + \mu \big[\nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} - \tfrac{2}{3}(\nabla \cdot \mathbf{u})\mathbf{I} \big]~ $$ 该方程也可以写成另一种常见形式 \(^\text{[7]}\)： $$ \boldsymbol{\sigma} = -p\mathbf{I} + \mu \big(\nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}}\big) + \big(\zeta - \tfrac{2}{3}\mu\big)(\nabla \cdot \mathbf{u})\mathbf{I}.~ $$ 需要注意的是，在可压缩流的情况下，压力 $p$ 不再单纯与各向同性应力项成比例，因为多了一个体黏度项：$p = -\tfrac{1}{3} \operatorname{tr}(\boldsymbol{\sigma})+ \zeta (\nabla \cdot \mathbf{u})$.

　　 同时，偏应力张量 $\boldsymbol{\sigma}'$ 仍与剪切应力张量 $\boldsymbol{\tau}$ 相同（也就是说，牛顿流体的偏应力部分不包含法向应力分量），但相较于不可压缩情形，它多了一个与压缩性相关的项，依然与剪切黏度 $\mu$ 成正比： $$ \boldsymbol{\sigma}' = \boldsymbol{\tau} = \mu \big[\nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} - \tfrac{2}{3}(\nabla \cdot \mathbf{u})\mathbf{I} \big].~ $$ 需要强调的是，体黏度 $\zeta$ 和动力黏度 $\mu$ 不一定是常数。对于单一化学组分的流体，这两个传输系数通常取决于两个热力学变量，例如压力和温度。任何显式地将这些传输系数与守恒变量联系起来的方程，都被称为状态方程 \(^\text{[8]}\)。

　　 最一般形式的纳维–斯托克斯方程为：

　　 纳维–斯托克斯动量方程（对流形式） $$ \rho \frac{\mathrm{D} \mathbf{u}}{\mathrm{D} t} = \rho \left(\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} \right) = -\nabla p + \nabla \cdot \left\{ \mu \left[ \nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} - \tfrac{2}{3} (\nabla \cdot \mathbf{u}) \mathbf{I} \right] \right\} + \nabla \left[\zeta (\nabla \cdot \mathbf{u})\right] + \rho \mathbf{a}.~ $$ 用指标记号可以写为 \(^\text{[9]}\)：

　　 纳维–斯托克斯动量方程（指标形式） $$ \rho \left( \frac{\partial u_{i}}{\partial t} + u_{k} \frac{\partial u_{i}}{\partial x_{k}} \right) = -\frac{\partial p}{\partial x_{i}} + \frac{\partial}{\partial x_{k}} \left[ \mu \left( \frac{\partial u_{i}}{\partial x_{k}} + \frac{\partial u_{k}}{\partial x_{i}} - \tfrac{2}{3}\delta_{ik} \frac{\partial u_{l}}{\partial x_{l}} \right) \right] + \frac{\partial}{\partial x_{i}} \left( \zeta \frac{\partial u_{\ell}}{\partial x_{\ell}} \right) + \rho a_{i}.~ $$ 对应的守恒形式可通过质量连续性方程得到，因为在该条件下，动量方程左侧满足： $$ \rho \frac{\mathrm{D} \mathbf{u}}{\mathrm{D} t} = \frac{\partial}{\partial t}(\rho \mathbf{u}) + \nabla \cdot (\rho \mathbf{u} \otimes \mathbf{u}).~ $$ 最终得到：

　　 纳维–斯托克斯动量方程（守恒形式） $$ \frac{\partial}{\partial t}(\rho \mathbf{u}) + \nabla \cdot \left( \rho \mathbf{u} \otimes \mathbf{u} + \big[p - \zeta (\nabla \cdot \mathbf{u})\big]\mathbf{I} - \mu \left[ \nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} - \tfrac{2}{3} (\nabla \cdot \mathbf{u}) \mathbf{I} \right] \right) = \rho \mathbf{a}.~ $$ 关于第二黏度系数 $\zeta$ 的说明：第二黏度系数不仅依赖于压力和温度，还依赖于过程本身，因此它并不完全是一个纯粹的材料常数。示例：当声波以某一固定频率周期性压缩和膨胀流体单元时，第二黏度系数会依赖于声波的频率，这种依赖性称为色散。在某些情况下，$\zeta$ 可以近似认为是常数。在这种假设下，体黏度 $\zeta$ 的作用表现为：机械压力不再等同于热力学压力 \(^\text{[10]}\)，具体如下所示： $$ \nabla \cdot (\nabla \cdot \mathbf{u})\mathbf{I} = \nabla (\nabla \cdot \mathbf{u}),~ $$ $$ \bar{p} \equiv p - \zeta \,\nabla \cdot \mathbf{u}.~ $$ 这里，$\bar{p}$ 表示修正后的机械压力。

　　 然而，这种差异在大多数情况下通常会被忽略（也就是说，只要我们不涉及声吸收、激波衰减等需要考虑第二黏度系数 $\zeta$ 的过程 \(^\text{[11]}\)），做法是直接假设 $\zeta = 0$。这种假设被称为斯托克斯假设 \(^\text{[12]}\)。斯托克斯假设的有效性可以通过动理论以及单原子气体的实验得到验证 \(^\text{[13]}\)；而对于其他气体和液体，斯托克斯假设通常并不完全正确。在斯托克斯假设下，纳维–斯托克斯方程变为：

　　 纳维–斯托克斯动量方程（对流形式，斯托克斯假设） $$ \rho \frac{\mathrm{D} \mathbf{u}}{\mathrm{D} t} = \rho \left( \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla)\mathbf{u} \right) = -\nabla p + \nabla \cdot \left\{ \mu \left[ \nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} - \tfrac{2}{3}(\nabla \cdot \mathbf{u}) \mathbf{I} \right] \right\} + \rho \mathbf{a}.~ $$ 若假设动力黏度 $\mu$ 和体黏度 $\zeta$ 在空间中均为常数，对流形式的方程可以进一步简化。通过计算应力张量的散度：$\nabla \cdot (\nabla \mathbf{u}) = \nabla^2 \mathbf{u}$,$\nabla \cdot [(\nabla \mathbf{u})^{\mathrm{T}}] = \nabla (\nabla \cdot \mathbf{u})$ 最终得到可压缩纳维–斯托克斯动量方程 \(^\text{[14]}\)：

　　 纳维–斯托克斯动量方程（均匀剪切和体黏度，对流形式） $$ \frac{\mathrm{D}\mathbf{u}}{\mathrm{D}t} = -\frac{1}{\rho}\nabla p + \nu \nabla^2 \mathbf{u} + \left(\tfrac{1}{3}\nu + \xi \right)\nabla (\nabla \cdot \mathbf{u}) + \mathbf{a}.~ $$ 其中：$\displaystyle \frac{\mathrm{D}}{\mathrm{D}t}$ 是物质导数；$\nu = \frac{\mu}{\rho}$ 是剪切运动黏度；$\xi = \frac{\zeta}{\rho}$ 是体运动黏度。

　　 在守恒形式下，将流速的微分算子带到方程左侧，可写成： $$ \left( \frac{\partial}{\partial t} + \mathbf{u} \cdot \nabla - \nu \nabla^2 - \left(\tfrac{1}{3}\nu + \xi\right)\nabla(\nabla \cdot) \right)\mathbf{u} = -\frac{1}{\rho}\nabla p + \mathbf{a}.~ $$ 对流加速度项还可以重写为： $$ \mathbf{u} \cdot \nabla \mathbf{u} = (\nabla \times \mathbf{u}) \times \mathbf{u} + \tfrac{1}{2}\nabla \mathbf{u}^2,~ $$ 其中 $(\nabla \times \mathbf{u}) \times \mathbf{u}$ 被称为 Lamb 向量。

　　 在不可压缩流的特例下，压力会对流动施加约束，使得流体元的体积保持不变，即等容流，其速度场满足 $\nabla \cdot \mathbf{u} = 0$ 从而形成无散速度场 \(^\text{[15]}\)。

5. 不可压缩流

　　 不可压缩流体的动量纳维–斯托克斯方程基于以下关于柯西应力张量的假设 \(^\text{[5]}\)：

　　 这种本构方程也被称为牛顿黏性定律。动力黏度 $\mu$ 不一定是常数——即使在不可压缩流中，$\mu$ 也可能依赖于密度和压力。任何将这些传输系数之一明确表达为守恒变量函数的方程，都称为状态方程 \(^\text{[8]}\)。

　　 对于黏度均匀的情况，偏应力张量的散度为： $$ \nabla \cdot \boldsymbol{\tau} = 2\mu \nabla \cdot \boldsymbol{\varepsilon} = \mu \nabla \cdot (\nabla \mathbf{u} + \nabla \mathbf{u}^{\mathrm{T}}) = \mu \nabla^2 \mathbf{u},~ $$ 因为对于不可压缩流体，有：$\nabla \cdot \mathbf{u} = 0$.

　　 不可压缩性意味着不会出现密度波或压力波，例如声波或激波，因此如果需要研究这些现象，这种简化就不适用。然而，对于低马赫数（大约马赫数 $M \leq 0.3$）的情况，例如常温下空气风的建模，不可压缩流假设通常是合理的 \(^\text{[16]}\)。

　　 不可压缩纳维–斯托克斯方程（黏度均匀，对流形式） $$ \frac{D\mathbf{u}}{Dt} = \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla)\mathbf{u} = \nu \nabla^2 \mathbf{u} - \frac{1}{\rho} \nabla p + \frac{1}{\rho} \mathbf{f},~ $$ 其中：$\nu = \frac{\mu}{\rho}$ 称为运动黏度。

　　 通过将流速单独列出，可以得到另一种形式：

　　 不可压缩纳维–斯托克斯方程（黏度恒定，另一种对流形式） $$ \left( \frac{\partial}{\partial t} + \mathbf{u} \cdot \nabla - \nu \nabla^2 \right)\mathbf{u} = -\frac{1}{\rho} \nabla p + \frac{1}{\rho} \mathbf{f}.~ $$ 如果整个流体区域内的密度是恒定的（换句话说，所有流体单元的密度相同，即 $\rho$ 为常数），方程进一步化简为：

　　 不可压缩纳维–斯托克斯方程（密度和黏度均恒定，对流形式） $$ \frac{D\mathbf{u}}{Dt} = \nu \nabla^2 \mathbf{u} - \nabla\left(\frac{p}{\rho}\right) + \frac{1}{\rho} \mathbf{f},~ $$ 其中：$\displaystyle \frac{p}{\rho}$ 称为单位压力水头。

　　 在不可压缩流中，压力场满足泊松方程 \(^\text{[9]}\)： $$ \nabla^2 p = -\rho \frac{\partial u_i}{\partial x_k} \frac{\partial u_k}{\partial x_i} = -\rho \frac{\partial^2 (u_i u_k)}{\partial x_k \partial x_i},~ $$ 该方程是通过对动量方程取散度得到的。

　　 层流示例

　　 仔细观察方程中每一项的物理意义（可与柯西动量方程对照）：

图
图 2

　　 高阶项，即剪切应力散度 $\nabla \cdot \boldsymbol{\tau}$，在这种情况下简化为速度矢量的拉普拉斯项 $\mu \nabla^2 \mathbf{u}$\(^\text{[18]}\)。这个拉普拉斯项可以解释为：某一点的速度与该点附近小体积内速度平均值的差异。这意味着，对于牛顿流体而言，黏性就像动量的扩散，与热传导的机理非常相似。事实上，如果忽略对流项，不可压缩的纳维–斯托克斯方程会退化为一个矢量扩散方程（即斯托克斯方程）；但在一般情况下，对流项始终存在，因此不可压缩的纳维–斯托克斯方程属于对流–扩散方程的范畴。

　　 在常见的情形下，如果外部场是保守场，则有： $$ \mathbf{g} = -\nabla \varphi~ $$ 定义水头为： $$ h \equiv w + \varphi~ $$ 于是，可以将所有源项合并为一个项，得到带保守外场的不可压缩纳维–斯托克斯方程： $$ \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla)\mathbf{u} - \nu \nabla^2 \mathbf{u} = -\nabla h.~ $$ 意义与应用

　　 这种形式的不可压缩纳维–斯托克斯方程，在密度和黏度均匀并且外力为保守场的情况下，称为液压学的基本方程。它的应用范围非常广，求解区域通常是三维或更低维的欧几里得空间**，并且常会设定一个正交坐标系，以显式写出标量偏微分方程形式。

　　 坐标系说明

　　 三维正交坐标系主要包括：笛卡尔坐标系,柱坐标系,球坐标系;在笛卡尔坐标下，将纳维–斯托克斯矢量方程展开相对简单，而且这种展开与所采用的欧几里得空间维数影响不大； 对于一阶项（如变化项和对流项），即使在非笛卡尔正交坐标系下，处理也相对直接； 但对于高阶项（例如来自偏应力散度的两项，这两项正是纳维–斯托克斯方程与欧拉方程的区别所在），则需要使用张量分析来推导在非笛卡尔正交坐标系下的表达式。液压学基本方程的一个特殊情况就是伯努利方程。

　　 不可压缩纳维–斯托克斯方程可以看作是由两部分正交方程组成的复合方程： $$ \begin{aligned} \frac{\partial \mathbf{u}}{\partial t} &=\Pi^S\left(-(\mathbf{u} \cdot \nabla)\mathbf{u} + \nu \nabla^2 \mathbf{u}\right) + \mathbf{f}^S,\\ \rho^{-1} \nabla p &=\Pi^I\left(-(\mathbf{u} \cdot \nabla)\mathbf{u} + \nu \nabla^2 \mathbf{u}\right) + \mathbf{f}^I. \end{aligned}~ $$ 其中：$\Pi^S$ 和 $\Pi^I$ 分别是无散投影算子与无旋投影算子，满足 $\Pi^S + \Pi^I = 1$；$\mathbf{f}^S$ 和 $\mathbf{f}^I$ 分别表示体力中的非保守部分和保守部分。这一分解源自亥姆霍兹定理，也称为**向量微积分基本定理。第一个方程是一个无压力项的速度控制方程；第二个方程则给出压力关于速度的函数关系，且与压力泊松方程相关。

　　 三维空间中投影算子的显式形式由亥姆霍兹定理给出： $$ \Pi^S \mathbf{F}(\mathbf{r}) = \frac{1}{4\pi} \nabla \times \int \frac{\nabla' \times \mathbf{F}(\mathbf{r}')} {|\mathbf{r} - \mathbf{r}'|} \, dV', \qquad \Pi^I = 1 - \Pi^S,~ $$ 二维情况下结构类似。由此可见，该控制方程实际上是一个类似库仑定律或毕奥–萨伐尔定律的积分–微分方程，这使得数值计算并不方便。

　　 已有研究证明，这种形式能得到与原始纳维–斯托克斯方程完全一致的速度解 \(^\text{[19]}\)： $$ (\mathbf{w}, \frac{\partial \mathbf{u}}{\partial t}) = -(\mathbf{w}, (\mathbf{u} \cdot \nabla)\mathbf{u}) -\nu (\nabla \mathbf{w} : \nabla \mathbf{u}) + (\mathbf{w}, \mathbf{f}^S),~ $$ 其中：$\mathbf{w}$ 是满足适当边界条件的无散测试函数；投影通过无散函数空间和无旋函数空间的正交性实现。

　　 这种弱形式非常适合采用有限元方法求解无散流动，尤其是在离散形式下。在接下来的部分，可以进一步探讨如何利用这种无压力的速度控制方程来求解压力驱动（如泊肃叶流，Poiseuille flow）问题。

　　 速度控制方程中没有直接出现压力力，表明该方程并不是严格的动力方程，而更像是一种运动学方程，其中无散条件起到了类似守恒方程的作用。这意味着，常见的说法——“不可压缩流体中的压力是用来维持无散条件的”——并不完全准确。

不可压缩纳维–斯托克斯方程的弱形式

　　 强形式

　　 考虑一个牛顿流体，其密度 $\rho$ 恒定，定义在区域 $$ \Omega \subset \mathbb{R}^d \quad (d = 2, 3)~ $$ 上，其边界为 $$ \partial \Omega = \Gamma_D \cup \Gamma_N,~ $$ 其中：$\Gamma_D$：施加 Dirichlet 边界条件的部分；$\Gamma_N$：施加 Neumann 边界条件的部分；且两部分互不重叠：$\Gamma_D \cap \Gamma_N = \emptyset$。该系统在时间区间 $(0, T)$ 内的方程为 \(^\text{[20]}\)： $$ \begin{cases} \rho \dfrac{\partial \mathbf{u}}{\partial t} + \rho (\mathbf{u} \cdot \nabla)\mathbf{u} - \nabla \cdot \boldsymbol{\sigma}(\mathbf{u}, p) = \mathbf{f}, & \text{在 } \Omega \times (0, T) \\[6pt]\\ \nabla \cdot \mathbf{u} = 0, & \text{在 } \Omega \times (0, T) \\[6pt]\\ \mathbf{u} = \mathbf{g}, & \text{在 } \Gamma_D \times (0, T) \\[6pt]\\ \boldsymbol{\sigma}(\mathbf{u}, p) \hat{\mathbf{n}} = \mathbf{h}, & \text{在 } \Gamma_N \times (0, T) \\[6pt]\\ \mathbf{u}(0) = \mathbf{u}_0, & \text{在 } \Omega \times \{0\} \end{cases}~ $$ $\mathbf{u}$ 表示流体速度，$p$ 表示流体压力，$\mathbf{f}$ 是给定的体力项，$\hat{\mathbf{n}}$ 是指向 $\Gamma_N$ 外侧的单位法向量，$\boldsymbol{\sigma}(\mathbf{u}, p)$ 是黏性应力张量，其定义为[20]： $$ \boldsymbol{\sigma}(\mathbf{u}, p) = -p\mathbf{I} + 2\mu \boldsymbol{\varepsilon}(\mathbf{u}).~ $$ 其中：$\mu$：流体的动力黏度；$\mathbf{I}$：二阶单位张量；$\boldsymbol{\varepsilon}(\mathbf{u})$：应变率张量，定义为[20]： $$ \boldsymbol{\varepsilon}(\mathbf{u}) = \frac{1}{2} \left( \nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} \right).~ $$ 函数 $\mathbf{g}$ 和 $\mathbf{h}$ 分别是给定的 Dirichlet 边界条件和 Neumann 边界条件，而 $\mathbf{u}_0$ 是初始条件。第一条方程是动量平衡方程；第二条方程是质量守恒方程，也称为连续性方程。

　　 当假设动力黏度 $\mu$ 为常数时，可以使用以下向量恒等式： $$ \nabla \cdot \left(\nabla \mathbf{f}\right)^{\mathrm{T}} = \nabla \left(\nabla \cdot \mathbf{f}\right),~ $$ 利用质量守恒，可以将动量方程中总应力张量的散度重新表示为 \(^\text{[20]}\)： $$ \begin{aligned} \nabla \cdot \boldsymbol{\sigma}(\mathbf{u}, p) &= \nabla \cdot \big(-p\mathbf{I} + 2\mu \boldsymbol{\varepsilon}(\mathbf{u})\big)\\ &= -\nabla p + 2\mu \nabla \cdot \boldsymbol{\varepsilon}(\mathbf{u})\\ &= -\nabla p + 2\mu \nabla \cdot \left[\tfrac{1}{2} \big(\nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}}\big) \right]\\ &= -\nabla p + \mu \big(\Delta \mathbf{u} + \nabla \cdot (\nabla \mathbf{u})^{\mathrm{T}}\big)\\ &= -\nabla p + \mu \big(\Delta \mathbf{u} + \nabla (\nabla \cdot \mathbf{u})\big)\\ &= -\nabla p + \mu \,\Delta \mathbf{u} \end{aligned}~ $$ 由于不可压缩条件 $\nabla \cdot \mathbf{u} = 0$，最后一项消失。

　　 此外，Neumann 边界条件可以重写为 \(^\text{[20]}\)： $$ \boldsymbol{\sigma}(\mathbf{u}, p)\,\hat{\mathbf{n}} = \big(-p\mathbf{I} + 2\mu \boldsymbol{\varepsilon}(\mathbf{u})\big)\,\hat{\mathbf{n}} = -p \,\hat{\mathbf{n}} + \mu \,\frac{\partial \mathbf{u}}{\partial \hat{\mathbf{n}}}.~ $$ 弱形式

　　 为了得到纳维–斯托克斯方程的弱形式，首先考虑动量方程 \(^\text{[20]}\)：

　　 $$ \rho \frac{\partial \mathbf{u}}{\partial t} -\mu \Delta \mathbf{u} +\rho (\mathbf{u} \cdot \nabla)\mathbf{u} +\nabla p = \mathbf{f},~ $$ 然后选取一个定义在合适空间 $V$ 中的测试函数 $\mathbf{v}$，将动量方程乘以该测试函数，并对区域 $\Omega$ 进行积分 \(^\text{[20]}\)： $$ \int_{\Omega} \rho \frac{\partial \mathbf{u}}{\partial t} \cdot \mathbf{v} - \int_{\Omega} \mu \Delta \mathbf{u} \cdot \mathbf{v} + \int_{\Omega} \rho (\mathbf{u} \cdot \nabla)\mathbf{u} \cdot \mathbf{v} + \int_{\Omega} \nabla p \cdot \mathbf{v} = \int_{\Omega} \mathbf{f} \cdot \mathbf{v}.~ $$ 通过分部积分处理扩散项和压力项，并利用高斯定理[20]：

　　 $$ -\int_{\Omega} \mu \Delta \mathbf{u} \cdot \mathbf{v} = \int_{\Omega} \mu \nabla \mathbf{u} \cdot \nabla \mathbf{v} - \int_{\partial \Omega} \mu \frac{\partial \mathbf{u}}{\partial \hat{\mathbf{n}}} \cdot \mathbf{v},~ $$ $$ \int_{\Omega} \nabla p \cdot \mathbf{v} = -\int_{\Omega} p \, \nabla \cdot \mathbf{v} + \int_{\partial \Omega} p \, \mathbf{v} \cdot \hat{\mathbf{n}}.~ $$ 利用上述关系，可以得到弱形式方程 \(^\text{[20]}\)： $$ \begin{aligned} &\int_{\Omega} \rho \frac{\partial \mathbf{u}}{\partial t} \cdot \mathbf{v} + \int_{\Omega} \mu \nabla \mathbf{u} \cdot \nabla \mathbf{v} + \int_{\Omega} \rho (\mathbf{u} \cdot \nabla) \mathbf{u} \cdot \mathbf{v} - \int_{\Omega} p \, \nabla \cdot \mathbf{v} \\ &= \int_{\Omega} \mathbf{f} \cdot \mathbf{v} + \int_{\partial \Omega} \left( \mu \frac{\partial \mathbf{u}}{\partial \hat{\mathbf{n}}} - p \hat{\mathbf{n}} \right) \cdot \mathbf{v}, \quad \forall \mathbf{v} \in V. \end{aligned}~ $$ 同样的方法，将连续性方程乘以一个属于空间 $Q$ 的测试函数 $q$，并在区域 $\Omega$ 上积分 \(^\text{[20]}\)： $$ \int_{\Omega} q \, (\nabla \cdot \mathbf{u}) = 0, \quad \forall q \in Q.v~ $$ 测试函数的空间定义 $$ \begin{aligned} V &= [H_0^1(\Omega)]^d = \big\{ \mathbf{v} \in [H^1(\Omega)]^d : \mathbf{v} = \mathbf{0} \ \text{在 } \Gamma_D \big\},\\ Q &= L^2(\Omega), \end{aligned}~ $$ 其中：$V$：速度测试函数空间，Dirichlet 边界 $\Gamma_D$ 上的值为 0；$Q$：压力测试函数空间。由于测试函数 $\mathbf{v}$ 在 $\Gamma_D$ 上为 0，并结合 Neumann 边界条件，可以将边界积分写为 \(^\text{[20]}\)： $$ \int_{\partial \Omega} \left( \mu \frac{\partial \mathbf{u}}{\partial \hat{\mathbf{n}}} - p \hat{\mathbf{n}} \right) \cdot \mathbf{v} = \underbrace{ \int_{\Gamma_D} \left( \mu \frac{\partial \mathbf{u}}{\partial \hat{\mathbf{n}}} - p \hat{\mathbf{n}} \right) \cdot \mathbf{v} }_{\mathbf{v}=0 \ \text{在 } \Gamma_D} + \int_{\Gamma_N} \underbrace{ \left( \mu \frac{\partial \mathbf{u}}{\partial \hat{\mathbf{n}}} - p \hat{\mathbf{n}} \right) }_{\mathbf{h} \ \text{在 } \Gamma_N} \cdot \mathbf{v} = \int_{\Gamma_N} \mathbf{h} \cdot \mathbf{v}.~ $$ 弱形式的最终表达

　　 找到一个函数 $\mathbf{u}$ 属于： $$ \mathbf{u} \in L^2\big(\mathbb{R}^+; [H^1(\Omega)]^d\big) \;\cap\; C^0\big(\mathbb{R}^+; [L^2(\Omega)]^d\big)~ $$ 使得： $$ \begin{cases} \displaystyle \int_{\Omega} \rho \frac{\partial \mathbf{u}}{\partial t} \cdot \mathbf{v} + \int_{\Omega} \mu \nabla \mathbf{u} \cdot \nabla \mathbf{v} + \int_{\Omega} \rho (\mathbf{u} \cdot \nabla) \mathbf{u} \cdot \mathbf{v} - \int_{\Omega} p \, (\nabla \cdot \mathbf{v}) = \int_{\Omega} \mathbf{f} \cdot \mathbf{v} + \int_{\Gamma_N} \mathbf{h} \cdot \mathbf{v}, & \forall \mathbf{v} \in V, \\[8pt] \displaystyle \int_{\Omega} q \, (\nabla \cdot \mathbf{u}) = 0, & \forall q \in Q. \end{cases}~ $$

离散速度

　　 在将问题域进行区域划分并在划分后的区域上定义基函数之后，控制方程的离散形式可以表示为： $$ \left(\mathbf{w}_i, \frac{\partial \mathbf{u}_j}{\partial t}\right) = -\left(\mathbf{w}_i, (\mathbf{u} \cdot \nabla)\mathbf{u}_j\right) -\nu \left(\nabla \mathbf{w}_i : \nabla \mathbf{u}_j\right) +\left(\mathbf{w}_i, \mathbf{f}^S\right).~ $$ 理想情况下，应选择能够体现不可压缩流动本质特性的基函数——即单元必须是无散的。虽然速度是关注的主要变量，但根据亥姆霍兹定理，流函数或矢量势的存在是必要的。此外，在不存在压力梯度的情况下，确定流体流动可以通过以下方式完成：二维情形：指定通道两侧的流函数值差；三维情形：指定通道周围矢量势切向分量的线积分（由斯托克斯定理给出流动）。

　　 我们进一步将讨论范围限定在连续 Hermite 有限元，这些单元至少具备一阶导数自由度。 利用这种方法，可以从大量板弯曲问题文献中选择候选的三角形或矩形单元，因为这些单元的梯度中包含导数分量。在二维情形下，标量的梯度与旋度显然是正交的，其表达式如下： $$ \nabla \varphi = \begin{pmatrix} \dfrac{\partial \varphi}{\partial x} \dfrac{\partial \varphi}{\partial y} \end{pmatrix}, \qquad \nabla \times \varphi = \begin{pmatrix} \dfrac{\partial \varphi}{\partial y} -\dfrac{\partial \varphi}{\partial x} \end{pmatrix}.~ $$ 通过采用连续板弯曲单元，并交换导数自由度的位置，同时适当地改变某些分量的符号，可以生成多种流函数单元族，用于构造满足不可压缩条件的数值模型。

　　 对标量流函数单元取旋度可以得到无散速度单元 \(^\text{[21][22]}\)。要求流函数单元连续，可以保证速度在单元交界面上的法向分量连续，这正是确保这些界面上散度为零的必要条件。

　　 边界条件的应用也相对简单：在无流动边界上，流函数保持常数；在无滑移边界上，满足无滑移速度条件；在开放通道上，通道两侧的流函数差值决定了流量；开放边界则无需施加边界条件，但在某些问题中可使用一致的值。

　　 这些条件本质上都是 Dirichlet 边界条件。由此建立的代数方程构造简单，但由于方程是非线性的，仍需通过迭代求解线性化方程。

　　 类似的思路可以推广到三维问题，但从二维扩展到三维并非直接完成，因为势函数是矢量形式，而三维中梯度与旋度之间不存在二维情形下那种简单关系。

压力恢复

　　 从速度场中恢复压力非常简单。压力梯度的离散弱形式方程为： $$ (\mathbf{g}_i, \nabla p) = -(\mathbf{g}_i, (\mathbf{u} \cdot \nabla)\mathbf{u}_j) -\nu (\nabla \mathbf{g}_i : \nabla \mathbf{u}_j) +(\mathbf{g}_i, \mathbf{f}^I),~ $$ 任何符合条件的标量有限元都可以用来求解压力。不过，如果还需要压力的梯度场，可以选择使用标量 Hermite 元来表示压力。对于测试/加权函数 $\mathbf{g}_i$，则可以选取通过压力单元的梯度构造的无旋矢量单元。

6. 非惯性参考系

　　 在旋转参考系下，由于物质导数项的存在，方程中会引入一些有趣的伪力。设：惯性参考系为 $K$，非惯性参考系为 $K'$，它相对于 $K$ 以速度 $\mathbf{U}(t)$ 做平移运动，并以角速度 $\mathbf{\Omega}(t)$ 做旋转。

　　 则从非惯性系观察到的纳维–斯托克斯动量方程为： $$ \begin{aligned} \rho \left( \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} \right) &= -\nabla p + \nabla \cdot \left\{ \mu \left[ \nabla \mathbf{u} + (\nabla \mathbf{u})^{\mathrm{T}} -\frac{2}{3}(\nabla \cdot \mathbf{u}) \mathbf{I} \right] \right\} + \nabla \big[\zeta (\nabla \cdot \mathbf{u})\big] + \rho \mathbf{f} \\ &\quad - \rho \left[ 2 \mathbf{\Omega} \times \mathbf{u} + \mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{x}) + \frac{d\mathbf{U}}{dt} + \frac{d\mathbf{\Omega}}{dt} \times \mathbf{x} \right]. \end{aligned}~ $$ 符号与含义：$\mathbf{x}$ 和 $\mathbf{u}$：在非惯性参考系中测量的位置和速度；括号中四项伪力分别对应：科里奥利加速度：$2 \mathbf{\Omega} \times \mathbf{u}$；离心加速度：$\mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{x})$；平移加速度：$\frac{d\mathbf{U}}{dt}$；角加速度：$\frac{d\mathbf{\Omega}}{dt} \times \mathbf{x}$。

7. 其他方程

　　 纳维–斯托克斯方程严格来说只是动量守恒的表达式。若要完整描述流体流动，还需要更多信息，其具体需求取决于所采用的假设。这些附加信息可能包括：边界条件（如无滑移条件、毛细表面条件等）；质量守恒；能量平衡；状态方程。

不可压缩流体的连续性方程

　　 无论采用何种流动假设，质量守恒的表述通常都是必要的。这可以通过**质量连续性方程实现，如本文 “广义连续介质方程” 部分所述，公式如下： $$ \frac{\mathbf{D} m}{\mathbf{D} t} = \iiint\limits_V \left( \frac{\mathbf{D} \rho}{\mathbf{D} t} + \rho (\nabla \cdot \mathbf{u}) \right) \, dV~ $$ $$ \frac{\mathbf{D} \rho}{\mathbf{D} t} + \rho (\nabla \cdot \mathbf{u}) = \frac{\partial \rho}{\partial t} + (\nabla \rho) \cdot \mathbf{u} + \rho (\nabla \cdot \mathbf{u}) = \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0~ $$ 对于密度 $\rho$ 恒定的流体介质，称为不可压缩流体。因此，密度 $\rho$ 对时间的变化率 $\displaystyle \left(\frac{\partial \rho}{\partial t}\right)$ 和密度的梯度 $\displaystyle (\nabla \rho)$ 都等于 0。在这种情况下，通用的连续性方程：$\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0$ 简化为：$\rho (\nabla \cdot \mathbf{u}) = 0$ 进一步假设密度 $\rho$ 是非零常数 $(\rho \neq 0)$，则可将方程两边同时除以 $\rho$，得到： $$ \nabla \cdot \mathbf{u} = 0~ $$ 这一关系 $\nabla \cdot \mathbf{u} = 0$ 表明：流速向量 $\mathbf{u}$ 的散度为零；换句话说，对于不可压缩流体，流速场是一个无散场或散度为零的向量场。值得注意的是，这一关系可以结合向量拉普拉斯算子展开：$\nabla^2 \mathbf{u}= \nabla (\nabla \cdot \mathbf{u})- \nabla \times (\nabla \times \mathbf{u})$ 由于不可压缩流体满足 $\nabla \cdot \mathbf{u} = 0$，可进一步写为： $$ \nabla^2 \mathbf{u} = -(\nabla \times (\nabla \times \mathbf{u})) = -(\nabla \times \vec{\omega}),~ $$

8. 二维不可压缩流体的流函数

　　 对不可压缩 Navier–Stokes 方程取旋度后，可以消去压力项。这种做法在二维笛卡尔流动（或者退化的三维情况，满足 $u_z = 0$ 且所有物理量与 $z$ 无关）时尤其直观，此时方程可化简为：$x$ 方向动量方程： $$ \rho \left( \frac{\partial u_x}{\partial t} + u_x \frac{\partial u_x}{\partial x} + u_y \frac{\partial u_x}{\partial y} \right) = -\frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 u_x}{\partial x^2} + \frac{\partial^2 u_x}{\partial y^2} \right) + \rho g_x~ $$ $y$ 方向动量方程： $$ \rho \left( \frac{\partial u_y}{\partial t} + u_x \frac{\partial u_y}{\partial x} + u_y \frac{\partial u_y}{\partial y} \right) = -\frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 u_y}{\partial x^2} + \frac{\partial^2 u_y}{\partial y^2} \right) + \rho g_y~ $$ 将第一条方程对 $y$ 求偏导，第二条方程对 $x$ 求偏导，然后相减，可以消去压力项以及所有保守力项。对于不可压缩流体，定义流函数 $\psi$： $$ u_x = \frac{\partial \psi}{\partial y}, \quad u_y = -\frac{\partial \psi}{\partial x},~ $$ 即可无条件满足质量连续性方程（只要流函数是连续的）。这样，不可压缩牛顿流体的二维动量与质量守恒可以简化为单个方程： $$ \frac{\partial}{\partial t}\left(\nabla^2 \psi\right) + \frac{\partial \psi}{\partial y} \frac{\partial}{\partial x} \left(\nabla^2 \psi\right) - \frac{\partial \psi}{\partial x} \frac{\partial}{\partial y} \left(\nabla^2 \psi\right) = \nu \nabla^4 \psi,~ $$ 其中：$\nabla^4$ 表示二维双调和算子，$\nu = \dfrac{\mu}{\rho}$ 表示运动黏度。这个方程还可以更紧凑地表示为雅可比行列式形式： $$ \frac{\partial}{\partial t}\left(\nabla^2 \psi\right) + \frac{\partial(\psi, \nabla^2 \psi)}{\partial (y, x)} = \nu \nabla^4 \psi.~ $$ 这一单一方程结合适当的边界条件，就能够完整描述二维流体流动，并且只需要运动黏度 $\nu$ 作为参数。特别地，当左侧项假设为零时，该方程退化为缓慢流动的描述方程。

　　 在轴对称流动中，可以使用另一种流函数形式，称为斯托克斯流函数，只需一个标量函数即可描述不可压缩流动的速度分量。

　　 不可压缩的纳维–斯托克斯方程是一个微分代数方程，其一个不便之处在于：没有明确的机制来显式推进压力随时间的演化。因此，许多研究都致力于在计算过程中部分或完全消除压力项。采用流函数形式可以去掉压力项，但这种方法仅适用于二维问题，并且代价是：引入高阶导数，丢失了作为主要研究变量的速度分量。

9. 性质

非线性

　　 纳维–斯托克斯方程在一般情况下是非线性偏微分方程，几乎在所有真实情形中都保持非线性特征 \(^\text{[23][24]}\)。在某些特定情况下，例如一维流动或斯托克斯流动（Stokes flow，或缓慢流动 creeping flow），方程可以简化为线性方程。这种非线性：使得大多数问题难以甚至无法解析求解；也是方程能够描述湍流现象的主要原因。

　　 非线性源于对流加速度，即速度随空间位置变化所引起的加速度。因此，任何含有对流成分的流动——无论是否湍流——都必然表现出非线性。一种典型的对流但层流（非湍流）的情形是：黏性流体（如油）通过一个小的收敛喷嘴的流动。这种流动，无论能否被精确解析，都通常可以通过理论和数值方法进行深入研究和理解 \(^\text{[25]}\)。

湍流

　　 湍流是许多流体流动中表现出的随时间变化的混沌行为。一般认为，它是由整个流体的惯性引起的：即时间相关的加速度和对流加速度共同作用的结果；因此，在惯性效应较小的情况下，流动往往呈现层流状态（雷诺数用于量化流动受惯性影响的程度）。普遍相信（但尚未完全确定）纳维–斯托克斯方程能够正确描述湍流现象。\(^\text{[26]}\)

　　 对于湍流流动的纳维–斯托克斯方程进行数值求解极为困难，因为湍流涉及显著不同尺度的混合长度，要获得稳定解，需要极其精细的网格划分，这会导致计算时间变得极为不可行，无论是用于计算还是直接数值模拟。尝试用层流求解器来处理湍流时，往往会得到不稳定的随时间变化的结果，无法正确收敛。为解决这一问题，在实际计算流体力学（CFD）建模中，通常使用经过时间平均的方程，例如雷诺平均纳维–斯托克斯方程（RANS），并结合湍流模型。常见的湍流模型包括 Spalart–Allmaras 模型、k–ω 模型、k–ε 模型以及 SST 模型，这些模型通过增加多组附加方程来封闭 RANS 方程。大涡模拟（LES）也可用于对这些方程进行数值求解。这种方法在计算时间和内存需求上比 RANS 更昂贵，但因显式解析了较大的湍流尺度，因而能够获得更好的模拟结果。

适用性

　　 结合附加方程（例如质量守恒方程）和合理设置的边界条件，纳维–斯托克斯方程似乎能够准确地描述流体的运动；甚至在湍流的情况下，其平均结果也与现实世界中的观测值大体一致。

　　 纳维–斯托克斯方程假设所研究的流体是连续介质（可以无限细分，而不是由原子或分子等粒子组成），且其运动速度不是相对论速度。在非常小的尺度或极端条件下，由离散分子组成的真实流体，其行为会与纳维–斯托克斯方程描述的连续流体有所不同。例如，在存在高梯度的流动中，流体内部层的毛细效应会显现出来。\(^\text{[27]}\) 当问题的 Knudsen 数较大时，玻尔兹曼方程可能是更合适的替代方案。\(^\text{[28]}\) 若仍无法满足需求，则可能需要借助分子动力学方法或各种混合方法。\(^\text{[29]}\)

　　 另一个局限性在于方程本身的复杂性。对于常见的流体类别，已经存在经过时间检验的数学表述；但将纳维–斯托克斯方程应用于较为特殊的流体类别时，往往会产生极其复杂的数学形式，甚至引发新的研究问题。因此，这些方程通常被用于描述牛顿流体，即粘性模型为线性的情况；而对于其他类型流体（如血液）的流动，目前仍不存在完全通用的数学模型。\(^\text{[30]}\)

10. 在具体问题中的应用

　　 纳维–斯托克斯方程，即使针对特定流体明确写出后，仍然具有相当通用的性质，因此在具体问题中的正确应用方式可能千差万别。这部分是因为可建模的问题范围极其广泛，从最简单的静压分布，到由表面张力驱动的复杂多相流，都可以用它来描述。

　　 通常，将方程应用于具体问题时，首先需要对流动做出一些假设，并建立初始条件和边界条件；随后，可能还需要进行尺度分析，以进一步简化问题。

图
图 3：（a）平行流与（b）径向流的可视化

平行流

　　 假设存在稳态、平行、单向的、非对流的压差驱动流动，流体位于两块平行板之间，则经过无量纲化处理后得到如下边值问题： $$ \frac{\mathrm{d}^2 u}{\mathrm{d} y^2} = -1; \quad u(0) = u(1) = 0.~ $$ 这里的边界条件为无滑移条件。该问题的流场解可以很容易求出： $$ u(y) = \frac{y - y^2}{2}.~ $$ 在此基础上，可以进一步轻松推导出其他感兴趣的物理量，例如黏性阻力或总体流量。

径向流

　　 当问题稍微复杂一些时，难度就会显著增加。一个看似对上述平行流的温和扩展，就是考虑平行板之间的径向流动；这类流动涉及对流项，从而引入非线性。其速度场可由函数 $f(z)$ 表示，并需满足以下方程： $$ \frac{\mathrm{d}^2 f}{\mathrm{d} z^2} + R f^2 = -1; \quad f(-1) = f(1) = 0.~ $$ 当将纳维–斯托克斯方程写出并结合流动假设后（同时解出压力梯度）就会得到这个常微分方程。由于非线性项的存在，该问题在解析求解上极为困难（尽管可以得到冗长的隐式解，但它涉及椭圆积分和三次多项式的根）。当参数 $R$（用适当的尺度定义的雷诺数）大于约 1.41（约值，并非 $\sqrt{2}$）时，还会出现解是否存在的问题。这是一个流动假设失效的典型例子，也反映出高雷诺数流动所带来的复杂性。\(^\text{[31]}\)

对流

　　 一种可以用纳维–斯托克斯方程描述的自然对流现象是瑞利–贝纳德对流。由于其在理论分析和实验研究中都相对容易实现，因此成为研究最为广泛的对流现象之一。

11. 纳维–斯托克斯方程的精确解

　　 纳维–斯托克斯方程在某些情况下是有精确解的。一些退化情形（即方程中的非线性项为零）包括泊肃叶流、库埃特流和振荡斯托克斯边界层。除此之外，还有一些更有趣的情形，即完整非线性方程的解，例如：杰弗里–哈梅尔流，冯·卡门旋转流，停滞点流，朗道–斯奎尔射流泰勒–格林涡，对于三维不可压缩的纳维–斯托克斯方程，利用二次自变量的库默尔函数，可以给出随时间变化的自相似解。而对于可压缩的纳维–斯托克斯方程，在以多方状态方程作为闭合条件时，随时间变化的自相似解则可通过二次自变量的惠特克函数表达。

　　 需要注意的是，这些精确解的存在并不意味着它们一定是稳定的；在更高的雷诺数下，流动中仍可能发展出湍流。在附加假设下，还可以将方程的各个分量部分进行分离。

　　 二维示例

　　 例如，在一个无界平面区域内，假设流体是二维、不可压缩且稳态的，在极坐标 $(r, \varphi)$ 下，其速度分量 $(u_r, u_\varphi)$ 和压力 $p$ 表达式为：\(^\text{[38]}\) $$ \begin{aligned} u_r &= \frac{A}{r}, \\[6pt] u_\varphi &= B\left(\frac{1}{r} - r^{\frac{A}{\nu} + 1}\right), \\[6pt] p &= -\frac{A^2 + B^2}{2r^2} - \frac{2B^2 \nu r^{\frac{A}{\nu}}}{A} + \frac{B^2 r^{\left(\frac{2A}{\nu} + 2\right)}}{\frac{2A}{\nu} + 2}. \end{aligned}~ $$ 其中，$A$ 和 $B$ 是任意常数。该解在 $r \geq 1$ 且 $A < -2\nu$ 的区域内有效。

　　 在直角坐标系下，当黏度为零（$\nu = 0$）时，该解可写为： $$ \begin{aligned} \mathbf{v}(x, y) &= \frac{1}{x^2 + y^2} \begin{pmatrix} Ax + By \\ Ay - Bx \end{pmatrix}, \\[6pt] p(x, y) &= -\frac{A^2 + B^2}{2(x^2 + y^2)}. \end{aligned}~ $$ 三维示例

　　 例如，在一个无界欧几里得空间中，假设流动是三维、不可压缩、稳态且黏度为零（$\nu = 0$）的径向流动，在直角坐标系 $(x, y, z)$ 下，速度矢量 $\mathbf{v}$ 和压力 $p$ 表达式如下： $$ \begin{aligned} \mathbf{v}(x, y, z) &= \frac{A}{x^2 + y^2 + z^2} \begin{pmatrix} x \\ y \\ z \end{pmatrix}, \\[6pt] p(x, y, z) &= -\frac{A^2}{2(x^2 + y^2 + z^2)}. \end{aligned}~ $$ 在 $x = y = z = 0$ 处，该解存在奇点。

三维稳态涡旋解

图
图 4：Hopf 纤维化流线的线框模型

　　 一种没有奇点的稳态解可以通过研究沿 Hopf 纤维化轨迹的流动得到。设 $r$ 为内环的常数半径，则有一组解为：\(^\text{[39]}\) $$ \begin{aligned} \rho(x, y, z) &= \frac{3B}{r^2 + x^2 + y^2 + z^2}, \\[6pt] p(x, y, z) &= \frac{-A^2 B}{\left(r^2 + x^2 + y^2 + z^2\right)^3}, \\[6pt] \mathbf{u}(x, y, z) &= \frac{A}{\left(r^2 + x^2 + y^2 + z^2\right)^2} \begin{pmatrix} 2(-ry + xz) \\[6pt] 2(rx + yz) \\[6pt] r^2 - x^2 - y^2 + z^2 \end{pmatrix}, \\[6pt] g &= 0, \\[6pt] \mu &= 0. \end{aligned}~ $$ 对于任意常数 $A$ 和 $B$。这是一个无黏性气体（可压缩流体）的解，其密度、速度和压力在远离原点时都会趋近于零。（需要注意的是，这并不是克雷千禧难题中所指的问题，因为千禧难题针对的是不可压缩流体，即密度 $\rho$ 为常数的情况；同时，这个解也没有涉及纳维–斯托克斯方程在湍流特性上的唯一性问题。）还值得注意的是，该速度矢量的分量正好对应于毕达哥拉斯四元组参数化的形式。对于相同的速度场，还可以选择其他的密度和压力分布。

　　 密度与压力的其他选择

　　 对于相同的速度矢量，还可以选择另一组压力和密度分布，在这种情况下，压力和密度在原点趋近于零，并且在中心环（$z = 0, \; x^2 + y^2 = r^2$）处达到最大值： $$ \begin{aligned} \rho(x, y, z) &= \frac{20B(x^2 + y^2)}{\left(r^2 + x^2 + y^2 + z^2\right)^3}, \\[6pt] p(x, y, z) &= \frac{-A^2 B}{\left(r^2 + x^2 + y^2 + z^2\right)^4} + \frac{-4A^2 B(x^2 + y^2)}{\left(r^2 + x^2 + y^2 + z^2\right)^5}. \end{aligned}~ $$ 实际上，更一般地，对于任意多项式函数 $f$，都可以得到如下形式的简单解，其中密度为： $$ \rho(x, y, z) = \frac{1}{r^2 + x^2 + y^2 + z^2} \, f\!\left(\frac{x^2 + y^2}{\left(r^2 + x^2 + y^2 + z^2\right)^2}\right).~ $$

三维黏性周期解

　　 文献 \(^\text{[40]}\) 描述了两类完全三维的黏性周期解。这些解定义在一个三维环面 $\mathbb{T}^3 = [0, L]^3$ 上，并分别表现为正螺旋度和负螺旋度。以下是正螺旋度解： $$ \begin{aligned} u_x &= \frac{4\sqrt{2}}{3\sqrt{3}}\,U_0 \left[ \sin\left(kx-\pi/3\right) \cos\left(ky+\pi/3\right) \sin\left(kz+\pi/2\right) - \cos\left(kz-\pi/3\right) \sin\left(kx+\pi/3\right) \sin\left(ky+\pi/2\right) \right] e^{-3\nu k^2 t}, \\[6pt] u_y &= \frac{4\sqrt{2}}{3\sqrt{3}}\,U_0 \left[ \sin\left(ky-\pi/3\right) \cos\left(kz+\pi/3\right) \sin\left(kx+\pi/2\right) - \cos\left(kx-\pi/3\right) \sin\left(ky+\pi/3\right) \sin\left(kz+\pi/2\right) \right] e^{-3\nu k^2 t}, \\[6pt] u_z &= \frac{4\sqrt{2}}{3\sqrt{3}}\,U_0 \left[ \sin\left(kz-\pi/3\right) \cos\left(kx+\pi/3\right) \sin\left(ky+\pi/2\right) - \cos\left(ky-\pi/3\right) \sin\left(kz+\pi/3\right) \sin\left(kx+\pi/2\right) \right] e^{-3\nu k^2 t}, \end{aligned}~ $$ 其中：$k = 2\pi/L$ 是波数；各速度分量经过归一化处理，使得在 $t=0$ 时，单位质量的平均动能为：$U_0^2/2$.压力场可以通过速度场求得：$p = p_0 - \rho_0 \| \mathbf{u} \|^2 / 2$,其中 $p_0$ 和 $\rho_0$ 分别为压力和密度的参考值。由于该解属于 Beltrami 流，涡量场与速度场平行。对于正螺旋度的情况，有：$\boldsymbol{\omega} = \sqrt{3} \, k \, \mathbf{u}$.这些解可以看作是二维经典 Taylor–Green 涡的三维推广。

12. Wyld 图

　　 Wyld 图是一种记录图，用于表示通过连续介质力学基本方程的微扰展开得到的纳维–斯托克斯方程。它们类似于量子场论中的费曼图，也是对姆斯季斯拉夫·克尔迪什在流体动力学非平衡过程研究中提出的方法的一种扩展 $citation needed$。换句话说，这些图可以通过引入与伪随机函数相关的概率分布中的随机过程，将流体颗粒的相关性和相互作用纳入建模，从而用图形化方式描述湍流流体中的（往往是）湍流现象 $41$。

13. 三维表示

　　 需要注意的是，本节中的公式使用了简化的偏导数记号，例如 $\partial_x u$ 表示 $u$ 对 $x$ 的偏导数；$\partial_y^2 f_\theta$ 表示 $f_\theta$ 对 $y$ 的二阶偏导数。

　　 2022 年的一篇研究论文提出了一种低成本、动态、递归的三维湍流流动纳维–斯托克斯方程求解方法 $42$。在适当短的时间尺度内，湍流的动力学表现出确定性特征。

笛卡尔坐标系

　　 从纳维–斯托克斯方程的一般形式出发，将速度向量展开为 $\mathbf{u} = (u_x, u_y, u_z)$（有时分别记为 $u, v, w$），可以将矢量方程显式写为如下三分量形式：

　　 $x$-方向： $$ \begin{aligned} \rho \big( \partial_t u_x + u_x \partial_x u_x + u_y \partial_y u_x + u_z \partial_z u_x \big) &= -\partial_x p + \mu \big( \partial_x^2 u_x + \partial_y^2 u_x + \partial_z^2 u_x \big) \\ &\quad + \frac{1}{3} \mu \,\partial_x \big( \partial_x u_x + \partial_y u_y + \partial_z u_z \big) + \rho g_x \end{aligned}~ $$ $y$-方向： $$ \begin{aligned} \rho \big( \partial_t u_y + u_x \partial_x u_y + u_y \partial_y u_y + u_z \partial_z u_y \big) &= -\partial_y p + \mu \big( \partial_x^2 u_y + \partial_y^2 u_y + \partial_z^2 u_y \big) \\ &\quad + \frac{1}{3} \mu \,\partial_y \big( \partial_x u_x + \partial_y u_y + \partial_z u_z \big) + \rho g_y \end{aligned}~ $$ $z$-方向： $$ \begin{aligned} \rho \big( \partial_t u_z + u_x \partial_x u_z + u_y \partial_y u_z + u_z \partial_z u_z \big) &= -\partial_z p + \mu \big( \partial_x^2 u_z + \partial_y^2 u_z + \partial_z^2 u_z \big) \\ &\quad + \frac{1}{3} \mu \,\partial_z \big( \partial_x u_x + \partial_y u_y + \partial_z u_z \big) + \rho g_z \end{aligned}~ $$ 请注意，重力已作为体力项纳入计算，参数 $g_x$、$g_y$、$g_z$ 的取值取决于重力相对于所选坐标系的方向。

　　 连续性方程表示为： $$ \partial_t \rho + \partial_x (\rho u_x) + \partial_y (\rho u_y) + \partial_z (\rho u_z) = 0.~ $$ 当流动为不可压缩流时，流体质点的密度 $\rho$ 不会随时间变化，其物质导数为零：$\frac{\mathrm{D} \rho}{\mathrm{D} t} = 0$.

　　 此时，连续性方程简化为： $$ \partial_x u_x + \partial_y u_y + \partial_z u_z = 0.~ $$ 因此，在不可压缩的纳维–斯托克斯方程中，黏性项的第二部分将消失（参见 “不可压缩流” 部分）。

　　 这一系统由四个方程组成，是应用最广泛、研究最深入的形式。尽管与其他形式相比更为简洁，但它仍然是一个非线性的偏微分方程系统，其解析解依然非常难以获得。

柱坐标系

　　 将笛卡尔坐标系下的纳维–斯托克斯方程进行变量转换，可以得到柱坐标 $(r, \varphi, z)$ 下的动量方程 \(^\text{[16][43]}\)：

　　 $r$ 方向：

　　 $$ \begin{aligned} \rho \big( \partial_t u_r + u_r \partial_r u_r + \frac{u_\varphi}{r} \partial_\varphi u_r + u_z \partial_z u_r - \frac{u_\varphi^2}{r} \big) &= -\partial_r p \\ &\quad + \mu \Big( \frac{1}{r}\partial_r(r \partial_r u_r) + \frac{1}{r^2}\partial_\varphi^2 u_r + \partial_z^2 u_r - \frac{u_r}{r^2} - \frac{2}{r^2}\partial_\varphi u_\varphi \Big) \\ &\quad + \frac{1}{3}\mu \partial_r \Big( \frac{1}{r}\partial_r(r u_r) + \frac{1}{r}\partial_\varphi u_\varphi + \partial_z u_z \Big) + \rho g_r \end{aligned}~ $$ $\varphi$ 方向： $$ \begin{aligned} \rho \big( \partial_t u_\varphi + u_r \partial_r u_\varphi + \frac{u_\varphi}{r} \partial_\varphi u_\varphi + u_z \partial_z u_\varphi + \frac{u_r u_\varphi}{r} \big) &= -\frac{1}{r} \partial_\varphi p \\ &\quad + \mu \Big( \frac{1}{r} \partial_r(r \partial_r u_\varphi) + \frac{1}{r^2} \partial_\varphi^2 u_\varphi + \partial_z^2 u_\varphi - \frac{u_\varphi}{r^2} + \frac{2}{r^2} \partial_\varphi u_r \Big) \\ &\quad + \frac{1}{3}\mu \frac{1}{r} \partial_\varphi \Big( \frac{1}{r}\partial_r(r u_r) + \frac{1}{r}\partial_\varphi u_\varphi + \partial_z u_z \Big) + \rho g_\varphi \end{aligned}~ $$ $z$ 方向： $$ \begin{aligned} \rho \big( \partial_t u_z + u_r \partial_r u_z + \frac{u_\varphi}{r} \partial_\varphi u_z + u_z \partial_z u_z \big) &= -\partial_z p \\ &\quad + \mu \Big( \frac{1}{r} \partial_r(r \partial_r u_z) + \frac{1}{r^2} \partial_\varphi^2 u_z + \partial_z^2 u_z \Big) \\ &\quad + \frac{1}{3}\mu \partial_z \Big( \frac{1}{r}\partial_r(r u_r) + \frac{1}{r}\partial_\varphi u_\varphi + \partial_z u_z \Big) + \rho g_z \end{aligned}~ $$ 重力在各方向上的分量通常并非恒定。然而，在大多数应用中，要么选择合适的坐标系使重力分量为常数，要么假设重力被压力场抵消（例如，在水平管道中的流动通常会忽略重力效应和竖直方向上的压力梯度）。柱坐标下的连续性方程为： $$ \partial_t \rho + \frac{1}{r} \partial_r (\rho r u_r) + \frac{1}{r} \partial_\varphi (\rho u_\varphi) + \partial_z (\rho u_z) = 0.~ $$ 这种柱坐标形式是不可压缩纳维–斯托克斯方程中第二常见的表示方法（最常见的是笛卡尔坐标表示）。使用柱坐标的主要原因是利用对称性，从而使某个速度分量消失。一个非常常见的情形是轴对称流动，假设无切向速度（即 $u_\varphi = 0$），且所有物理量都与角向 $\varphi$ 无关。在这种情况下，方程组简化为：

　　 径向动量方程 $$ \rho \big( \partial_t u_r + u_r \partial_r u_r + u_z \partial_z u_r \big) = -\partial_r p + \mu \Big( \frac{1}{r}\partial_r (r \partial_r u_r) + \partial_z^2 u_r - \frac{u_r}{r^2} \Big) + \rho g_r~ $$ 轴向动量方程 $$ \rho \big( \partial_t u_z + u_r \partial_r u_z + u_z \partial_z u_z \big) = -\partial_z p + \mu \Big( \frac{1}{r}\partial_r (r \partial_r u_z) + \partial_z^2 u_z \Big) + \rho g_z~ $$ 连续性方程（不可压缩条件） $$ \frac{1}{r} \partial_r (r u_r) + \partial_z u_z = 0.~ $$

球坐标系

　　 在球坐标系下，纳维–斯托克斯方程的动量方程可以写成以下形式 \(^\text{[16]}\)。此处的角度约定为：$\theta$ 表示极角（或余纬角，colatitude），范围 $0 \leq \theta \leq \pi$；$\varphi$ 表示方位角；$r$ 表示径向坐标 \(^\text{[44]}\)。

　　 $r$ 方向动量方程 $$ \begin{aligned} \rho \Big( \partial_t u_r + u_r \partial_r u_r + \frac{u_\varphi}{r \sin\theta} \partial_\varphi u_r + \frac{u_\theta}{r} \partial_\theta u_r - \frac{u_\varphi^2 + u_\theta^2}{r} \Big) &= -\partial_r p \\[6pt] &\quad + \mu \Big( \frac{1}{r^2} \partial_r (r^2 \partial_r u_r) + \frac{1}{r^2 \sin^2\theta} \partial_\varphi^2 u_r + \frac{1}{r^2 \sin\theta} \partial_\theta (\sin\theta \partial_\theta u_r) \\ &\qquad - 2\frac{u_r + \partial_\theta u_\theta + u_\theta \cot\theta}{r^2} - \frac{2}{r^2 \sin\theta} \partial_\varphi u_\varphi \Big) \\[6pt] &\quad + \frac{1}{3}\mu \partial_r \Big( \frac{1}{r^2} \partial_r (r^2 u_r) + \frac{1}{r \sin\theta} \partial_\theta (u_\theta \sin\theta) + \frac{1}{r \sin\theta} \partial_\varphi u_\varphi \Big) \\ &\quad + \rho g_r \end{aligned}~ $$ $\varphi$ 方向动量方程 $$ \begin{aligned} \rho \Big( \partial_t u_\varphi + u_r \partial_r u_\varphi + \frac{u_\varphi}{r \sin\theta} \partial_\varphi u_\varphi + \frac{u_\theta}{r} \partial_\theta u_\varphi + \frac{u_r u_\varphi + u_\varphi u_\theta \cot\theta}{r} \Big) &= -\frac{1}{r \sin\theta} \partial_\varphi p \\[6pt] &\quad + \mu \Big( \frac{1}{r^2} \partial_r (r^2 \partial_r u_\varphi) + \frac{1}{r^2 \sin^2\theta} \partial_\varphi^2 u_\varphi + \frac{1}{r^2 \sin\theta} \partial_\theta (\sin\theta \partial_\theta u_\varphi) \\ &\qquad + \frac{2 \sin\theta \partial_\varphi u_r + 2 \cos\theta \partial_\varphi u_\theta - u_\varphi}{r^2 \sin^2\theta} \Big) \\[6pt] &\quad + \frac{1}{3}\mu \frac{1}{r \sin\theta} \partial_\varphi \Big( \frac{1}{r^2} \partial_r (r^2 u_r) + \frac{1}{r \sin\theta} \partial_\theta (u_\theta \sin\theta) + \frac{1}{r \sin\theta} \partial_\varphi u_\varphi \Big) \\ &\quad + \rho g_\varphi \end{aligned}~ $$ $\theta$ 方向动量方程 $$ \begin{aligned} \rho \Big( \partial_t u_\theta + u_r \partial_r u_\theta + \frac{u_\varphi}{r \sin\theta} \partial_\varphi u_\theta + \frac{u_\theta}{r} \partial_\theta u_\theta + \frac{u_r u_\theta - u_\varphi^2 \cot\theta}{r} \Big) &= -\frac{1}{r} \partial_\theta p \\[6pt] &\quad + \mu \Big( \frac{1}{r^2} \partial_r (r^2 \partial_r u_\theta) + \frac{1}{r^2 \sin^2\theta} \partial_\varphi^2 u_\theta + \frac{1}{r^2 \sin\theta} \partial_\theta (\sin\theta \partial_\theta u_\theta) \\ &\qquad + \frac{2}{r^2} \partial_\theta u_r - \frac{u_\theta + 2 \cos\theta \partial_\varphi u_\varphi}{r^2 \sin^2\theta} \Big) \\[6pt] &\quad + \frac{1}{3}\mu \frac{1}{r} \partial_\theta \Big( \frac{1}{r^2} \partial_r (r^2 u_r) + \frac{1}{r \sin\theta} \partial_\theta (u_\theta \sin\theta) + \frac{1}{r \sin\theta} \partial_\varphi u_\varphi \Big) \\ &\quad + \rho g_\theta \end{aligned}~ $$ 在球坐标系下，质量连续性方程可以写为：

　　 $$ \partial_t \rho + \frac{1}{r^2} \partial_r (\rho r^2 u_r) + \frac{1}{r \sin\theta} \partial_\varphi (\rho u_\varphi) + \frac{1}{r \sin\theta} \partial_\theta (\sin\theta \rho u_\theta) = 0.~ $$ 这些方程可以通过一些方法进行（轻微的）简化，例如从黏性项中提取 $\frac{1}{r^2}$ 作为公因子。但这种处理会不必要地改变拉普拉斯算子及其他相关项的结构，因此通常不建议这样做。

14. 参见

15. 参考文献

  1. McLean, Doug (2012). Continuum Fluid Mechanics and the Navier-Stokes Equations. Understanding Aerodynamics: Arguing from the Real Physics. John Wiley & Sons. pp. 13–78. ISBN 9781119967514. 纳维–斯托克斯方程的主要关系是质量、动量和能量的基本守恒定律。为了得到完整的方程组，还需要一个将温度、压力和密度联系起来的状态方程……
  2. Millennium Prize Problems—Navier–Stokes Equation, claymath.org, Clay Mathematics Institute, 2017 年 3 月 27 日，2015-12-22 存档，检索于 2017-04-02。
  3. Fefferman, Charles L. Existence and smoothness of the Navier–Stokes equation (PDF). claymath.org. Clay Mathematics Institute. 2015-04-15 存档 (PDF)，检索于 2017-04-02。
  4. Batchelor (1967) pp. 137 & 142.
  5. Batchelor (1967) pp. 142–148.
  6. Chorin, Alexandre E.; Marsden, Jerrold E. (1993). A Mathematical Introduction to Fluid Mechanics. p. 33.
  7. Bird, Stewart, Lightfoot. Transport Phenomena, 1st ed., 1960, eq. (3.2-11a).
  8. Batchelor (1967) p. 165.
  9. Landau, Lev Davidovich, and Evgenii Mikhailovich Lifshitz. Fluid Mechanics: Landau And Lifshitz: Course of Theoretical Physics, Volume 6. Vol. 6. Elsevier, 2013.
  10. Landau & Lifshitz (1987) pp. 44–45, 196.
  11. White (2006) p. 67.
  12. Stokes, G. G. (1845). On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids.
  13. Vincenti, W. G., Kruger Jr., C. H. (1975). Introduction to Physical Gas Dynamics. Huntington.
  14. Batchelor (1967) pp. 147 & 154.
  15. Batchelor (1967) p. 75.
  16. 参见 Acheson (1990).
  17. Abdulkadirov, Ruslan; Lyakhov, Pavel (2022-02-22). "Estimates of Mild Solutions of Navier–Stokes Equations in Weak Herz-Type Besov–Morrey Spaces". Mathematics. 10 (5): 680. doi:10.3390/math10050680. ISSN 2227-7390.
  18. Batchelor (1967) pp. 21 & 147.
  19. Temam, Roger (2001). Navier–Stokes Equations, Theory and Numerical Analysis. AMS Chelsea, pp. 107–112.
  20. Quarteroni, Alfio (2014-04-25). Numerical Models for Differential Problems (Second ed.). Springer. ISBN 978-88-470-5522-3.
  21. Holdeman, J. T. (2010). "A Hermite finite element method for incompressible fluid flow". Int. J. Numer. Methods Fluids, 64 (4): 376–408. Bibcode:2010IJNMF..64..376H. doi:10.1002/fld.2154. S2CID 119882803.
  22. Holdeman, J. T.; Kim, J. W. (2010). "Computation of incompressible thermal flows using Hermite finite elements". Comput. Meth. Appl. Mech. Eng., 199 (49–52): 3297–3304. Bibcode:2010CMAME.199.3297H. doi:10.1016/j.cma.2010.06.036.
  23. Potter, M.; Wiggert, D. C. (2008). Fluid Mechanics.*Schaum's Outlines. McGraw-Hill. ISBN 978-0-07-148781-8.
  24. Aris, R. (1989). Vectors, Tensors, and the Basic Equations of Fluid Mechanics. Dover Publications. ISBN 0-486-66110-5.
  25. Parker, C. B. (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. ISBN 0-07-051400-3.
  26. Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991. ISBN 3-527-26954-1 (Verlagsgesellschaft), ISBN 0-89573-752-3 (VHC Inc.).
  27. Gorban, A.N.; Karlin, I.V. (2016). "Beyond Navier–Stokes equations: capillarity of ideal gas". Contemporary Physics (综述文章), 58 (1): 70–90. arXiv:1702.00831. Bibcode:2017ConPh..58...70G. doi:10.1080/00107514.2016.1256123. S2CID 55317543.
  28. Cercignani, C. (2002). "The Boltzmann equation and fluid dynamics". 见 Friedlander, S.; Serre, D. (编), Handbook of Mathematical Fluid Dynamics, vol. 1, 阿姆斯特丹: North-Holland, pp. 1–70. ISBN 978-0444503305.
  29. Nie, X.B.; Chen, S.Y.; Robbins, M.O. (2004). "A continuum and molecular dynamics hybrid method for micro-and nano-fluid flow". Journal of Fluid Mechanics (研究论文), 500: 55–64. Bibcode:2004JFM...500...55N. doi:10.1017/S0022112003007225. S2CID 122867563.
  30. Öttinger, H.C. (2012). Stochastic Processes in Polymeric Fluids. 柏林, 海德堡: Springer Science & Business Media. doi:10.1007/978-3-642-58290-5. ISBN 9783540583530.
  31. Shah, Tasneem Mohammad (1972). "Analysis of the multigrid method". NASA Sti/Recon Technical Report N. 91: 23418. Bibcode:1989STIN...9123418S.
  32. Wang, C.Y. (1991). "Exact solutions of the steady-state Navier–Stokes equations". Annual Review of Fluid Mechanics, 23: 159–177. Bibcode:1991AnRFM..23..159W. doi:10.1146/annurev.fl.23.010191.001111.
  33. Landau & Lifshitz (1987) pp. 75–88.
  34. Ethier, C.R.; Steinman, D.A. (1994). "Exact fully 3D Navier–Stokes solutions for benchmarking". International Journal for Numerical Methods in Fluids, 19 (5): 369–375. Bibcode:1994IJNMF..19..369E. doi:10.1002/fld.1650190502.
  35. Barna, I.F. (2011). "Self-Similar Solutions of Three-Dimensional Navier–Stokes Equation". Communications in Theoretical Physics, 56 (4): 745–750. arXiv:1102.5504. Bibcode:2011CoTPh..56..745I. doi:10.1088/0253-6102/56/4/25.
  36. Barna, I.F.; Mátyás, L. (2014). "Analytic solutions for the three-dimensional compressible Navier-Stokes equation". Fluid Dynamics Research, 46 (5): 055508. arXiv:1309.0703. Bibcode:2014FlDyR..46e5508B. doi:10.1088/0169-5983/46/5/055508.
  37. "Navier Stokes Equations". [www.claudino.webs.com](http://www.claudino.webs.com). 2015-06-19 存档，检索于 2023-03-11。
  38. Ladyzhenskaya, O. A. (1969). The Mathematical Theory of Viscous Incompressible Flow (2nd ed.), 前言，第 xi 页。
  39. Kamchatno, A. M. (1982). "Topological solitons in magnetohydrodynamics" (PDF). Soviet Journal of Experimental and Theoretical Physics, 55 (1): 69. Bibcode:1982JETP...55...69K. 2016-01-28 从原始版本存档 (PDF)。
  40. Antuono, M. (2020). "Tri-periodic fully three-dimensional analytic solutions for the Navier–Stokes equations". Journal of Fluid Mechanics, 890 A23. Bibcode:2020JFM...890A..23A. doi:10.1017/jfm.2020.126. S2CID 216463266.
  41. McComb, W. D. (2008). Renormalization Methods: A Guide for Beginners. 牛津大学出版社, pp. 121–128. ISBN 978-0-19-923652-7.
  42. Georgia Institute of Technology (2022-08-29). "Physicists uncover new dynamical framework for turbulence". Proceedings of the National Academy of Sciences of the United States of America, 119 (34). Phys.org: e2120665119. doi:10.1073/pnas.2120665119. PMC 9407532. PMID 35984901. S2CID 251693676.
  43. de' Michieli Vitturi, Mattia. Navier–Stokes Equations in Cylindrical Coordinates, 检索于 2016-12-26。
  44. Eric W. Weisstein (2005-10-26). Spherical Coordinates, MathWorld, 检索于 2008-01-22。

16. 通用参考文献

17. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利