归并排序

贡献者： 有机物

　　 上文介绍了快速排序，本文将介绍归并排序。

　　 归并排序也是基于分治实现的。

　　 归并排序的算法步骤：

1. 确定分界点为 $\dfrac{l + r}{2}$，把一个序列分成两个大小为 $\dfrac{n}{2}$ 的子序列；
2. 先递归排序两个子序列；
3. 合并两个已排好序的子序列。

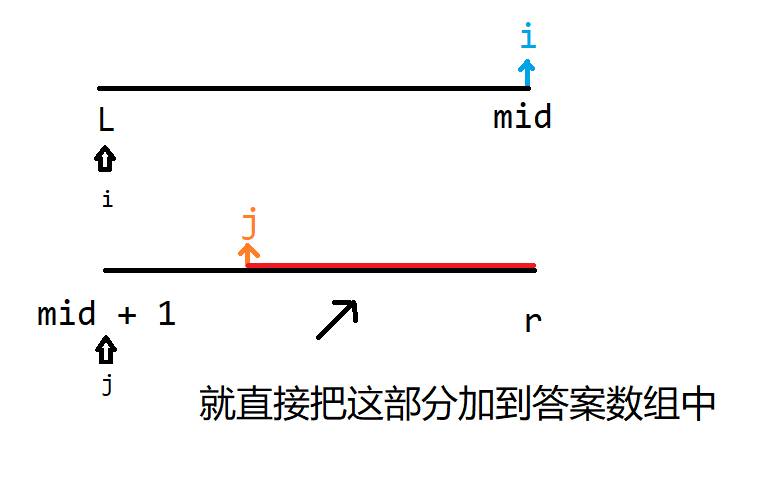
　　 归并排序的核心就是归并这一步，首先把一个序列分成两个子序列，然后维护两个指针，第一个指针指向第一个子序列的开头，第二个指针指向第二个子序列的开头。其实归并操作就是把两个子序列的值存到一个序列中然后输出出来，具体的做法是：每次判断一下两个指针所指向的值哪一个更小，把较小的的值插入到答案数组中，如果发现其中一个序列的指针已经直到末尾了，那么就退出循环，直接把另一个子序列的后面的值接到答案数组中（如图 $1$ 所示）。前提得保证两个子序列中的值都已排好序。

　　 时间复杂度：

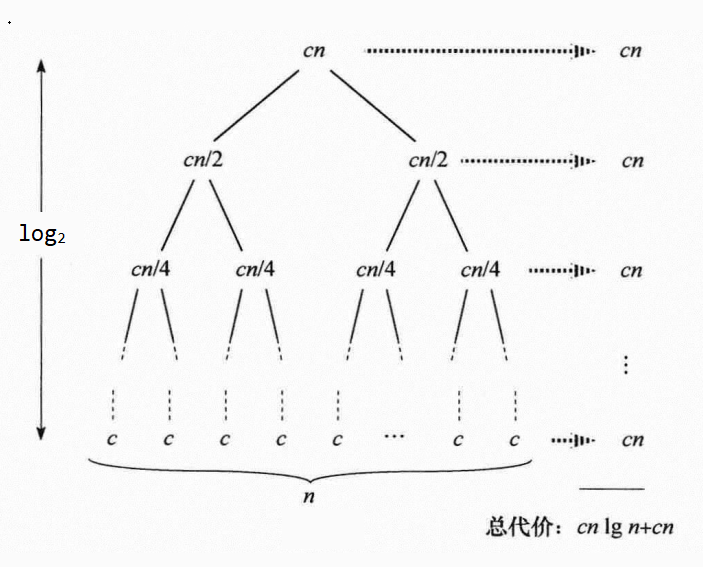
　　 归并排序的期望时间复杂度为 $\mathcal{O}(n \log_2 n)$，最坏时间复杂度也为 $\mathcal{O}(n \log_2 n)$，可以发现，归并的这一步操作是维护两个指针，两个指针会遍历完整个序列，所以时间复杂度为 $\mathcal{O}(n)$，然后递归每一层，每层有 $\frac{n}{2}$、$\frac{4}{n}$...，一共有 $\log_2 n$ 层，每层时间复杂度为 $\mathcal{O}(n)$，所以总共时间复杂度为 $\mathcal{O}(n \log_2 n)$。归并排序是稳定的。

　　 归并排序的代码：

int n, q[N], tmp[N];    // 需要额外开一个临时数组

void merge_sort(int q[], int l, int r)
{
    if (l == r) return;
    int mid = l + r >> 1;   // 分界点
    merge_sort(q, l, mid);  // 递归左边
    merge_sort(q, mid + 1, r);  // 递归右边
    
    int k = 0, i = l, j = mid + 1;  // i 为第一个子序列的起点，j 为第二个子序列的起点

    // 合并两个子序列
    while (i <= mid && j <= r)  // 当两个子序列都能往后走的时候
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];    // 较小者加入临时数组中
        else tmp[k ++ ] = q[j ++ ];
    
    while (i <= mid) tmp[k ++ ] = q[i ++ ]; // 如果第一个子序列还有元素，就直接加
    while (j <= r) tmp[k ++ ] = q[j ++ ];   // 第二个同理
    
    // j < k 可以写成 i <= r，j 为数组中的元素个数
    // i = l 的原因是：要把临时数组的值赋值给原数组原来的位置，因为 l、r 在一直变化
    for (int i = l, j = 0; j < k; i ++ , j ++ ) q[i] = tmp[j];  // 把临时数组赋值给原数组
}

merge_sort(q, 0, n - 1);    // 调用入口

　　 证明

　　 接下来证明一下归并排序的正确性，使用数学归纳法来证明。

　　 首先当序列长度 $n = 1$ 的时候，序列有序，成立。

　　 假设归并排序算法可以将任意长度小于 $n$ 的序列排好序。

　　 接下来证明归并排序算法可以将任意长度等于 $n$ 的序列排好序。

　　 看上面的代码中第 $7$ 行和第 $8$ 行，序列 l, mid 和 mid + 1, r 长度都小于 $n$，根据归纳假设，归并排序都可将这两个序列排好序。然后通过归并，可使得两个序列合并为一个有序序列。故对于长度等于 $n$ 的序列，归并排序都可将其排好序。

　　 所以对于任意长度的序列，归并排序都可将其排好。

　　 证毕。