蒙特卡罗方法（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：使用蒙特卡洛方法对正态分布的近似。

　　 蒙特卡罗方法，又称蒙特卡罗实验，是一类依赖重复随机抽样以获得数值解的广义计算算法。其基本思想是利用随机性来解决一些本质上可能是确定性的问题。该名称源自摩纳哥的蒙特卡罗赌场，该方法的主要发展者、数学家斯坦尼斯瓦夫·乌拉姆受到他叔叔赌博习惯的启发而命名。

　　 蒙特卡罗方法主要用于三类问题：优化问题，数值积分，从概率分布中抽样生成样本。此外，它还可以用于对输入存在高度不确定性的现象进行建模，例如评估核电站故障的风险。蒙特卡罗方法通常通过计算机模拟实现，能为那些无法解析求解或过于复杂的问题提供近似解。

　　 蒙特卡罗方法广泛应用于多个科学与工程领域，包括：物理、化学、生物学、统计学、人工智能、金融、密码学，也被应用于社会科学，如：社会学、心理学与政治学。它被认为是 20 世纪最重要且最具影响力的思想之一，并推动了众多科学与技术突破的实现。

　　 不过，蒙特卡罗方法也存在一些局限性和挑战，例如：精度与计算成本之间的权衡，维度灾难，随机数生成器的可靠性，结果的验证与确认。

1. 概述

　　 蒙特卡罗方法虽然形式多样，但通常遵循以下基本步骤：

  1. 定义可能输入的范围（即问题的定义域）；
  2. 从该范围内的概率分布中随机生成输入样本；
  3. 对每个输入进行确定性的计算，得到输出结果；
  4. 汇总（聚合）所有结果，以得到最终的估计或解。
图
图 2：蒙特卡罗方法用于近似计算 \(\pi\) 的值

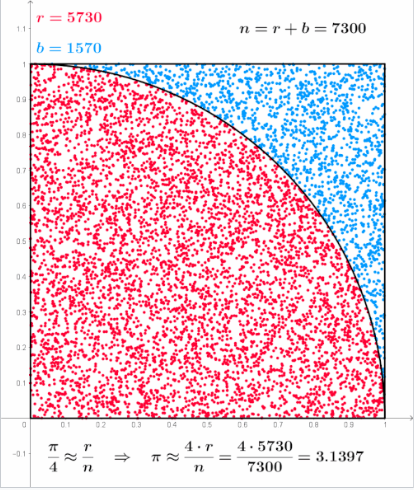
　　 例如，考虑一个内接于单位正方形的象限圆扇形。由于它们面积的比值是 $\frac{\pi}{4}$，因此可以使用蒙特卡罗方法来近似计算 $\pi$ 的值：\(^\text{[1]}\)

  1. 画一个正方形，并在其中内接一个象限圆（四分之一圆）；
  2. 在正方形内均匀随机撒布一定数量的点；
  3. 统计落在象限圆内的点的数量（即其到原点的距离小于 1 的点）；
  4. 象限内点数与总点数之比是两者面积比 $\frac{\pi}{4}$ 的估计值。 将该比值乘以 4，即可得到 $\pi$ 的估计值。

　　 在上述过程中，输入的定义域是包围该象限的正方形。可以通过在正方形内随机撒点（如撒沙粒）来生成输入，然后对每个输入执行一次计算，以判断它是否落在象限圆内。将结果汇总后，就可以得到最终的估计值——对 $\pi$ 的近似。

　　 这里有两个重要注意事项：

  1. 如果点不是均匀分布的，则估计结果将不准确；
  2. 随机点的数量越多，估计的精度就越高。

　　 蒙特卡罗方法的应用需要大量的随机数，因此它的发展极大地受益于伪随机数生成器的出现，这些生成器比早期所用的随机数表要高效得多。

2. 应用

　　 蒙特卡罗方法常用于物理和数学问题，尤其在其他方法难以或无法使用时最为有用。蒙特卡罗方法主要应用于三类问题：\(^\text{[2]}\)：优化问题，数值积分，从概率分布中生成样本（抽样）。

　　 在与物理相关的问题中，蒙特卡罗方法非常适用于模拟具有多个耦合自由度的系统，例如流体、无序材料、强耦合固体以及细胞结构等（参见：细胞 Potts 模型、相互作用粒子系统、McKean–Vlasov 过程、气体动力学模型）。

　　 其他应用示例包括：建模输入存在重大不确定性的现象，例如商业风险评估；在数学中，用于求解具有复杂边界条件的多维定积分；在系统工程问题中（如航天、石油勘探、飞机设计等），蒙特卡罗方法在预测失效概率、成本超支和进度延误方面，往往优于人类直觉或其他 “软性” 方法。\(^\text{[3]}\)

　　 从原理上讲，任何具有概率解释的问题都可以使用蒙特卡罗方法求解。根据大数定律，由某随机变量期望值所定义的积分可以通过该变量的独立样本的经验平均值（即样本均值）来近似。当所研究的随机变量具有参数化的概率分布时，数学家通常会使用马尔可夫链蒙特卡罗方法（MCMC）。\(^\text{[4][5][6]}\) 其核心思想是构造一个具有指定平稳分布的合适马尔可夫链模型。也就是说，在极限下，由 MCMC 方法生成的样本将来自目标分布。\(^\text{[7][8]}\) 根据遍历定理，该平稳分布可以通过 MCMC 采样器生成的随机状态的经验分布来近似。

　　 在其他类型的问题中，目标是从满足非线性演化方程的一系列概率分布中生成样本。这些概率分布的演化流总可以解释为某个马尔可夫过程的随机状态分布，其转移概率依赖于当前状态的分布（参见：McKean–Vlasov 过程、非线性滤波方程）。\(^\text{[9][10]}\) 在另外一些情形下，会出现采样复杂度不断上升的概率分布流，例如：随时间增长的路径空间模型，与降温参数相关的玻尔兹曼–吉布斯测度，以及其他类似模型。这些模型也可以看作是非线性马尔可夫链的随机状态分布的演化过程。\(^\text{[10][11]}\) 一种模拟此类复杂非线性马尔可夫过程的自然方法是：对该过程生成多个独立副本，用样本的经验分布来替代演化方程中未知的状态分布。与传统蒙特卡罗或 MCMC 方法不同，这些被称为平均场粒子方法的方法依赖于一组连续相互作用的样本。术语 “平均场” 指的是，每一个样本（也称为粒子、个体、行者、代理、实体或表型）都与过程的经验分布发生相互作用。当系统规模趋于无穷大时，这些随机的经验测度将收敛到非线性马尔可夫链中随机状态的确定性分布，从而粒子之间的统计相互作用也将消失。

3. 简单蒙特卡罗方法

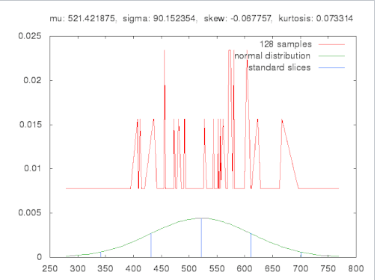
　　 假设我们希望知道某个总体的期望值 $\mu$（且已知该期望值存在），但无法通过公式直接计算。简单蒙特卡罗方法通过运行 $n$ 次模拟并对结果取平均，来对 $\mu$ 进行估计。

　　 该方法对模拟输入的概率分布没有限制，只要求以下几点：输入是随机生成的，输入彼此相互独立，$\mu$ 存在。只要 $n$ 足够大，所得估计值 $m$ 就能**任意接近于**真实值 $\mu$。更正式地说，对于任意 $\epsilon > 0$，都可以有 $|\mu - m| \leq \epsilon$\(^\text{[12]}\)

　　 通常用于计算 $m$ 的算法如下：

图
图 3

一个示例

　　 假设我们想知道：掷三个八面骰子，总点数至少为 $T$，我们期望需要掷多少次才能满足这一条件。我们知道该期望值是存在的。骰子的每次投掷是随机的且相互独立的，因此可以应用简单蒙特卡罗方法：

图
图 4

　　 如果 $n$ 足够大，则对于任意 $\epsilon > 0$，估计值 $m$ 将会落在真实值 $\mu$ 的 $\epsilon$ 范围内。

4. 确定足够大的 $n$

　　 通用公式

　　 设 $\epsilon = |\mu - m| > 0$，其中 $\mu$ 是真实期望值，$m$ 是蒙特卡罗估计值。首先，选择所需的置信水平——也就是希望在蒙特卡罗算法运行完成后，估计值 $m$ 落在 $\mu$ 的 $\epsilon$ 范围内的概率。设对应该置信水平的标准正态 $z$-分数为 $z$。

　　 设 $s^2$ 为估计方差（有时称为 “样本方差”），它是从一个相对较小的样本数量 $k$ 次模拟中计算得到的结果的方差。选择一个 $k$ 值；Driels 和 Shin 指出：“即使样本量比所需数量小一个数量级，这个估算结果通常也相当稳定。”\(^\text{[13]}\)

　　 以下算法可以单遍计算 $s^2$，同时最小化累积数值误差导致的错误结果风险：\(^\text{[12]}\)

图
图 5

　　 请注意，当算法运行结束时，$m_k$ 是从 $k$ 次模拟中得到的平均值。

　　 当满足以下条件时，$n$ 被认为是足够大的： $$ n \geq \frac{s^2 z^2}{\epsilon^2},^\text{[12][13]}~ $$ 如果 $n \leq k$，那么 $m_k = m$,说明已有的 $k$ 次模拟已足以保证 $m_k$ 在误差 $\epsilon$ 范围内逼近 $\mu$。如果 $n > k$,那么可以选择：重新 “从头开始” 运行 $n$ 次模拟，或因为已完成了 $k$ 次模拟，只需再运行 $n - k$ 次模拟，并将它们的结果加入原来的样本统计中即可：

图
图 6

　　 当模拟结果有界时的估算公式

　　 在所有模拟结果都有上下界的特例中，可以使用另一种估算公式。

　　 选择一个 $\epsilon$ 值，使其为 $\mu$ 与 $m$ 之间最大允许误差的两倍。设置信心水平 $\delta$，满足 $0 < \delta < 100$,并以百分比表示。假设每次模拟结果 $r_1, r_2, \ldots, r_i, \ldots, r_n$ 都满足 $a \leq r_i \leq b$，其中 $a$ 和 $b$ 是有限实数。若希望以至少 $\delta\%$ 的置信度满足 $|\mu - m| < \epsilon/2$,

　　 则应选择满足以下条件的 $n$： $$ n \geq 2(b - a)^2 \ln\left(2/(1 - (\delta/100))\right)/\epsilon^2~ $$ 例如，若 $\delta = 99\%$，则有：$n \geq 2(b - a)^2 \ln\left(2 / 0.01\right) /\epsilon^2 \approx 10.6(b - a)^2/\epsilon^2$.\(^\text{[12]}\)

5. 计算成本

　　 尽管蒙特卡罗方法在概念和算法上都非常简单，但其计算成本可能极其高昂。一般而言，该方法需要大量样本才能获得良好的近似结果，而如果每个样本的处理时间很长，那么总运行时间可能会大得无法接受。\(^\text{[14]}\) 尽管这一点在处理非常复杂的问题时是一个严重的限制，但该算法具有天然的 “尴尬并行性”，因此可以通过各种并行计算策略来降低这一高昂成本，使其达到可行的水平，例如使用：本地多处理器，计算集群，云计算，GPU（图形处理器），FPGA（现场可编程门阵列）等。\(^\text{[15][16][17][18]}\)

6. 历史

　　 在蒙特卡罗方法发展之前，模拟通常是用于测试已知的确定性问题，而统计抽样则被用于估算这些模拟中的不确定性。蒙特卡罗模拟则反其道而行之，利用概率性元启发式方法（如模拟退火）来求解确定性问题。

　　 蒙特卡罗方法的一个早期变种用于解决著名的布丰投针问题，该问题通过向平行等距条纹地板上投掷针来估算圆周率 $\pi$。20 世纪 30 年代，恩里科·费米在研究中子扩散问题时首次尝试了蒙特卡罗方法，但他并未发表相关研究成果。\(^\text{[19]}\)

　　 20 世纪 40 年代末，斯坦尼斯瓦夫·乌拉姆在美国洛斯阿拉莫斯国家实验室参与核武器项目期间，发明了现代版本的马尔可夫链蒙特卡罗方法。1946 年，洛斯阿拉莫斯的核武器物理学家正在研究核武器核心中中子的扩散问题。\(^\text{[19]}\) 尽管他们掌握了大部分必要的数据，比如中子在物质中与原子核发生碰撞之前的平均行进距离，以及中子发生碰撞后可能释放的能量等，但他们无法用传统的确定性数学方法解决这个问题。乌拉姆提出可以使用随机实验来处理此类问题。他这样回忆当时的灵感来源：

　　 我第一次尝试实践[蒙特卡罗方法]的想法，是源于 1946 年一个我在患病康复期间玩纸牌游戏（单人接龙）时想到的问题。当时我在想：用 52 张牌摆出的 Canfield 单人接龙游戏成功的几率有多大？我花了很长时间试图通过纯粹的组合计算来估算它，但后来我开始思考，是否有比 “抽象思维” 更实用的方法，比如干脆实际玩一百次，然后观察并统计成功次数。由于当时正值高速计算机新时代的开端，这个思路开始变得可行。我很快就联想到中子扩散问题及其他数学物理问题，进而更一般地思考，如何将某些微分方程所描述的过程转化为一系列可解释为随机操作的等效形式。后来（也是在 1946 年），我把这个想法讲给约翰·冯·诺依曼听，我们开始计划实际的计算工作。\(^\text{[20]}\)

　　 由于相关工作属于机密，冯·诺依曼和乌拉姆的研究需要一个代号。\(^\text{[21]}\) 他们的同事尼古拉斯·梅特罗波利斯提议使用 “蒙特卡罗” 这个名称，来源于摩纳哥的蒙特卡罗赌场，乌拉姆的叔叔曾常常向亲戚借钱去那里赌博。\(^\text{[19]}\) 蒙特卡罗方法在战后核武器进一步发展的模拟计算中发挥了核心作用，包括氢弹的设计，尽管当时的计算工具极其有限。1948 年春，冯·诺依曼、尼古拉斯·梅特罗波利斯及其他人使用 ENIAC 计算机进行了首次完全自动化的蒙特卡罗计算，模拟对象是裂变武器核心。\(^\text{[22]}\) 到了 20 世纪 50 年代，洛斯阿拉莫斯国家实验室在氢弹研发中大量应用了蒙特卡罗方法，该方法也逐渐在物理学、物理化学和运筹学等领域普及开来。兰德公司和美国空军是当时推广和资助蒙特卡罗方法研究的两大主要机构，该方法随后在许多不同领域中得到广泛应用。

　　 更为复杂的平均场类型粒子蒙特卡罗方法的理论，最迟在 20 世纪 60 年代中期就已开始发展，起始于亨利·P·麦基恩二世关于流体力学中出现的一类非线性抛物型偏微分方程的马尔可夫解释的研究。\(^\text{[23][24]}\) 而更早的一篇开创性文章由西奥多·E·哈里斯和赫尔曼·卡恩于 1951 年发表，文章中使用了平均场遗传类型的蒙特卡罗方法来估算粒子的传输能量。\(^\text{[25]}\) 平均场遗传类型的蒙特卡罗方法也被用作进化计算中的自然启发式搜索算法（又称元启发式算法，metaheuristic）。这种平均场计算技术的起源可以追溯到：1950 年和 1954 年，艾伦·图灵关于遗传型突变–选择学习机的工作，\(^\text{[26]}\) 以及尼尔斯·奥尔·巴里切利在新泽西普林斯顿高等研究院发表的相关论文。\(^\text{[27][28]}\)

　　 量子蒙特卡罗方法，特别是扩散蒙特卡罗方法，也可以被解释为对费曼–卡克路径积分的平均场粒子蒙特卡罗近似。\(^\text{[29][30][31][32][33][34][35]}\) 量子蒙特卡罗方法的起源通常归功于恩里科·费米和罗伯特·里希特迈尔，他们于 1948 年发展了中子链式反应的平均场粒子解释模型。\(^\text{[36]}\) 然而，第一个启发式或遗传型粒子算法（又称重采样蒙特卡罗或重构蒙特卡罗方法）用于估算量子系统基态能量（在约化矩阵模型中），是杰克·H·赫瑟林顿在 1984 年提出的。\(^\text{[35]}\) 在分子化学领域，使用遗传启发式粒子方法（也称为剪枝与增强策略）可以追溯到 1955 年，由马歇尔·N·罗森布鲁斯和阿丽安娜·W·罗森布鲁斯所开展的开创性工作。\(^\text{[37]}\)

　　 在高级信号处理与贝叶斯推断中使用序贯蒙特卡罗方法是较近才出现的进展。1993 年，Gordon 等人在其开创性论文中首次将蒙特卡罗重采样算法应用于贝叶斯统计推断。\(^\text{[38]}\) 作者将其算法命名为 “自助滤波器”，并指出与其他滤波方法相比，该算法不需要对状态空间或系统噪声作出任何假设。该领域的另一篇奠基性文章是北川源四郎关于相关的 “蒙特卡罗滤波器” 的研究。\(^\text{[39]}\) 同时期还有皮埃尔·德尔·莫拉尔，\(^\text{[40]}\) 以及 Himilcon Carvalho、Pierre Del Moral、André Monin 与 Gérard Salut 合作发表的关于粒子滤波器的研究论文，这些成果大多发表于 1990 年代中期。\(^\text{[41]}\) 实际上，在 1989 年至 1992 年间，P. Del Moral、J. C. Noyer、G. Rigal 和 G. Salut 在法国国家科学研究中心系统分析与架构实验室已在雷达/声纳与 GPS 信号处理领域开发出粒子滤波算法，这些工作曾以保密研究报告的形式提交给法国海军武器工程技术处、IT 公司 DIGILOG 及 LAAS-CNRS。\(^\text{[42][43][44][45][46][47]}\) 这些序贯蒙特卡罗方法可被理解为：带有相互作用重采样机制的接受–拒绝采样器。

　　 从 1950 年到 1996 年，所有关于序贯蒙特卡罗方法的出版物——包括在计算物理和分子化学中提出的剪枝与重采样蒙特卡罗方法——都提出了自然的、类启发式的算法，被应用于各种不同情境，但并未提供算法一致性的证明，也没有讨论估计偏差或基于谱系树与祖先树的算法结构。

　　 该领域的数学基础及对这些粒子算法的首个严格分析由皮埃尔·德尔·莫拉尔于 1996 年完成。\(^\text{[40][48]}\) 到了 20 世纪 90 年代末，具有可变粒子数量的分支型粒子方法也得到了发展，主要由丹·克里桑、杰西卡·盖恩斯和特里·里昂斯提出。\(^\text{[49][50][51]}\) 之后丹·克里桑、皮埃尔·德尔·莫拉尔与特里·里昂斯共同推动了进一步的研究。\(^\text{[52]}\)1999 年至 2001 年，P. Del Moral、A. Guionnet 和 L. Miclo 继续对该领域进行了拓展与深化。\(^\text{[30][53][54]}\)

7. 定义

　　 关于 “蒙特卡罗” 应如何定义，学界尚无统一共识。例如，Ripley\(^\text{[55]}\) 将大多数概率建模称为随机模拟，而将 “蒙特卡罗” 一词专用于蒙特卡罗积分和蒙特卡罗统计检验。Sawilowsky\(^\text{[56]}\) 则区分了模拟、蒙特卡罗方法与蒙特卡罗模拟三者的含义：模拟是对现实的一种虚构性再现；蒙特卡罗方法是一种用于求解数学或统计问题的技术手段；蒙特卡罗模拟是通过重复抽样来获取某种现象（或行为）的统计特性。

　　 Kalos 和 Whitlock\(^\text{[57]}\) 指出，这种区分并不总是容易维持的。例如，原子发射辐射是一个自然的随机过程，既可以直接对其进行模拟，也可以通过随机微分方程来描述其平均行为，而这些方程本身又可以通过蒙特卡罗方法求解。“实际上，同一段计算机代码既可以被视为一种‘自然模拟’，也可以被视为通过自然采样求解方程的方法。”

　　 可以通过 Gelman–Rubin 统计量来检验蒙特卡罗模拟的收敛性。

蒙特卡罗方法与随机数

　　 该方法的核心思想是：通过反复随机抽样与统计分析来计算结果。实际上，蒙特卡罗模拟本质上是一种随机实验，尤其适用于那些实验结果尚不明确的问题情境。蒙特卡罗模拟通常具有大量未知参数，其中许多参数难以通过实验手段获得。\(^\text{[58]}\) 蒙特卡罗模拟方法并不总是需要真正的随机数才能有效（尽管对于某些应用，如素性测试，不可预测性是至关重要的）。\(^\text{[59]}\) 许多实用的技术采用的是确定性的伪随机序列，这使得测试和重复运行模拟变得更加容易。通常，生成良好模拟所需的唯一标准是：伪随机序列在某种意义上看起来 “足够随机”。

　　 具体标准取决于实际应用，但通常来说，应满足一系列统计检验。最基本且最常见的检验之一是：当考虑序列中足够多的元素时，这些数应当呈均匀分布或符合其他期望分布。此外，相邻样本间的弱相关性通常也是所期望或必须具备的属性。

　　 Sawilowsky 对高质量蒙特卡罗模拟的标准进行了系统归纳，列出了以下关键特征：\(^\text{[56]}\)

　　 在模拟过程中，常通过伪随机数抽样算法将均匀分布的伪随机数转换为服从给定概率分布的随机变量。该过程确保模拟能在所需的分布特性下进行，进而提升结果的代表性。

　　 此外，在某些应用场景中，为克服随机抽样在覆盖空间时的不均匀性，常采用低偏差序列替代纯粹的随机或伪随机序列。这类方法通过实现更均匀的样本空间覆盖，通常能提供更高的收敛速度，从而提高模拟效率。基于此类序列的模拟被称为准蒙特卡罗方法。

　　 为研究伪随机数质量对蒙特卡罗模拟结果的影响，天体物理领域的研究者曾将 Intel RDRAND 指令集生成的加密级伪随机数与常用算法（如 Mersenne Twister）生成的伪随机数进行了对比。模拟场景为褐矮星无线电耀发的蒙特卡罗模拟，在生成 $10^7$ 个随机数的实验中，未观察到使用 RDRAND 与传统伪随机数生成器之间存在统计显著差异。\(^\text{[60]}\)

蒙特卡罗模拟 vs. “假设情景”（What-if）分析

　　 有些概率使用方式并不属于蒙特卡罗模拟，例如：采用单点估计进行的确定性建模。在这类方法中，模型中的每个不确定变量都被赋予一个 “最合理猜测” 的估计值。然后选择每个输入变量的情境（如最佳情况、最差情况或最可能情况），并记录相应结果。\(^\text{[61]}\)

　　 与之相反，蒙特卡罗模拟是从每个变量的概率分布中采样，生成数百甚至数千种可能的结果。随后对这些结果进行分析，从而得到不同结果发生的概率分布。\(^\text{[62]}\) 例如，将一个电子表格的建筑成本模型，分别以传统的 “假设情景” 方式和使用蒙特卡罗模拟（采用三角概率分布）方式运行比较会发现：蒙特卡罗分析的结果范围通常更窄，相较于 “假设情景” 分析。这是因为：“假设情景” 方法对所有情境赋予相等权重（详见：企业财务中的不确定性量化），而蒙特卡罗方法在概率极低的区域几乎不会采样。这种概率极低的样本被称为 “稀有事件”。

8. 应用领域

　　 蒙特卡罗方法在模拟输入存在显著不确定性、或系统具有多个耦合自由度的现象时尤其有用。其应用领域包括：

物理科学

　　 蒙特卡罗方法在计算物理、物理化学及相关的应用学科中具有极其重要的地位，并广泛应用于多个方向，例如：从复杂的量子色动力学（QCD）计算，到热防护罩与气动外形的设计，以及用于辐射剂量学计算的辐射输运建模。\(^\text{[63][64][65]}\) 在统计物理中，蒙特卡罗分子建模是计算分子动力学的一种替代方案；同时，蒙特卡罗方法也被用于计算简单粒子系统和聚合物系统的统计场论。\(^\text{[37][66]}\) 量子蒙特卡罗方法可用于求解多体量子系统问题。\(^\text{[9][10][29]}\) 在辐射材料科学中，用于模拟离子注入的二元碰撞近似（Binary Collision Approximation, BCA）通常基于蒙特卡罗方法来选择下一个碰撞原子。\(^\text{[67]}\) 在实验粒子物理中，蒙特卡罗方法用于：探测器的设计，探测器行为的建模，以及实验数据与理论模型的比对。在天体物理学中，蒙特卡罗方法被广泛用于不同任务，例如：模拟星系演化，\(^\text{[68]}\) 建模微波辐射在粗糙行星表面上的传播。\(^\text{[69]}\) 此外，蒙特卡罗方法也是现代天气预报中的集合模型的核心组成部分。

工程领域

　　 蒙特卡罗方法在工程中被广泛应用于灵敏度分析和过程设计中的定量概率分析。这是因为实际过程模拟往往存在变量间的相互作用、共线性以及非线性行为。例如：

气候变化与辐射强迫

　　 联合国政府间气候变化专门委员会（IPCC）在分析辐射强迫的概率密度函数时依赖于蒙特卡罗方法。\(^\text{[73]}\)

计算生物学

　　 蒙特卡罗方法广泛应用于计算生物学的多个领域，例如：系统发育树推断中的贝叶斯推断，或研究基因组、蛋白质和细胞膜等生物系统。\(^\text{[74][75]}\) 研究可以基于粗粒度模型或从头计算模型，具体取决于所需的精度。计算机模拟使研究者能够观察某个特定分子的局部环境变化，以判断是否发生某些化学反应。当物理实验不可行时，还可以进行思想实验，例如：断裂化学键、在特定位置引入杂质、改变局部或整体结构、施加外部场等。

计算机图形学

　　 路径追踪，有时也被称为蒙特卡罗光线追踪，是一种通过随机采样光线路径来渲染三维场景的方法。对任意像素进行多次采样后，所有样本的平均值最终将收敛到渲染方程的正确解。这使路径追踪成为目前已知最具物理精度的三维图形渲染方法之一。

应用统计学

　　 Sawilowsky\(^\text{[76]}\) 为统计学中的蒙特卡罗实验确立了标准。在应用统计学中，蒙特卡罗方法至少可用于以下四个方面：

  1. 比较在现实数据条件下，小样本下的统计量性能：虽然在经典理论分布（如正态分布、柯西分布）和渐近条件下（即样本无限大，处理效应无限小），可以计算统计量的第一类错误率和检验功效，但真实数据往往不服从这些理论分布。\(^\text{[77]}\)
  2. 实现比精确检验（如排列检验）更高效的假设检验方法：精确检验往往计算量极大甚至无法实现，而蒙特卡罗方法提供了一种比渐近分布临界值更准确、计算又更可行的替代方案。
  3. 在贝叶斯推断中，从后验分布中获取随机样本：通过这些样本可以近似并总结后验分布的所有关键特征。
  4. 高效地估计负对数似然函数的 Hessian 矩阵：这些随机估计值可进行平均，形成对 Fisher 信息矩阵的估计。\(^\text{[78][79]}\)

　　 蒙特卡罗方法也是近似随机化检验与置换检验之间的一种折中方案。近似随机化检验是基于所有置换中某个特定子集进行的，这通常需要进行大量记录和管理，以确保哪些置换已被考虑过。而蒙特卡罗方法则是基于预定数量的随机抽取置换样本。这种方式通过允许某些置换可能被重复抽取，在牺牲微小精度的同时，换来了更高的计算效率，因为无需追踪已抽取的置换。

游戏中的人工智能

　　 蒙特卡罗方法已被发展为一种称为蒙特卡罗树搜索的技术，用于在游戏中寻找最佳走法。可能的走法被组织成一棵搜索树，并通过大量随机模拟来估计每一步的长期潜力。对手的行为则由一个黑箱模拟器来表示。\(^\text{[80]}\)

　　 蒙特卡罗树搜索包含以下四个步骤：\(^\text{[81]}\)

  1. 从根节点出发，依次选择最优子节点，直到到达一个叶节点；
  2. 扩展该叶节点，并选择其一个子节点；
  3. 从该节点开始进行一次模拟游戏；
  4. 根据模拟结果更新该节点及其所有祖先节点的信息。

　　 随着大量模拟游戏的进行，某个表示某一步棋的节点的价值会逐渐上升或下降，理想情况下，该价值变化应反映该走法是否优秀。

　　 蒙特卡罗树搜索已成功应用于多种游戏中，例如：围棋（Go）\(^\text{[82]}\)Tantrix \(^\text{[83]}\) 战舰 \(^\text{[84]}\)Havannah \(^\text{[85]}\)Arimaa \(^\text{[86]}\)

设计与视觉呈现

　　 蒙特卡罗方法在求解辐射场与能量传输耦合的积分微分方程方面也非常高效，因此广泛应用于全局光照计算，可生成逼真的虚拟三维图像。该技术在多个领域都有应用，例如：视频游戏建筑与工业设计计算机生成影像（CG）电影特效等 \(^\text{[87]}\)

搜救行动

　　 美国海岸警卫队在其搜救建模软件 SAROPS（Search And Rescue Optimal Planning System）中采用了蒙特卡罗方法，用于计算搜救行动中船只的可能位置。每次模拟可基于所提供的变量随机生成多达一万个数据点。\(^\text{[88]}\) 系统随后会基于这些数据的外推结果生成搜索路径，以最大化：包围概率，发现概率，这两者相乘即为总体成功概率。最终，这一方法作为概率分布在现实中的实用应用，能够提供最快速、最有效的搜救策略，以节省生命与资源。\(^\text{[89]}\)

金融与商业

　　 蒙特卡罗模拟常用于评估风险与不确定性对不同决策结果的影响。它允许企业风险分析师将以下变量中的全部不确定性纳入考量：销售量，商品与劳动力价格，利率与汇率，特定风险事件（如合同取消、税法变更）

　　 在金融领域，蒙特卡罗方法常用于：评估项目投资价值（在业务部门或企业整体层面）其他财务估值， 它也可用于项目进度建模，模拟每个任务的最坏情况、最好情况和最可能持续时间，从而推导整个项目的进度分布。\(^\text{[90]}\) 此外，蒙特卡罗方法广泛用于：期权定价，违约风险分析，\(^\text{[91][92]}\) 估算医疗干预的财务影响。\(^\text{[93]}\)

法律

　　 蒙特卡罗方法曾用于评估一项在威斯康星州推行的女性法律援助项目的潜在价值，该项目旨在帮助女性成功申请骚扰或家庭暴力限制令。通过提供更强有力的法律支持，有望降低强奸与身体暴力的风险。然而，该项目涉及多个无法准确估计的变量，包括：限制令的实际效力，有无法律支持时的成功申请率 其他因素，该研究通过在这些变量上设置不同条件进行模拟，从而给出该项目整体成功水平的估计。\(^\text{[94]}\)

图书馆学

　　 蒙特卡罗方法也被用于模拟马来西亚不同图书类别的出版数量。模拟使用了：以往国家图书出版数据，各类图书在本地市场的价格，模拟结果用于判断马来西亚人偏好哪些图书类型，并与日本的图书出版情况进行对比分析。\(^\text{[95]}\)

其他领域

　　 纳西姆·尼古拉斯·塔勒布在其 2001 年出版的《被随机性欺骗》一书中，提到蒙特卡罗生成器是反图灵测试的真实案例：如果一个人的写作无法与机器生成内容区分出来，那他就可能被视为 “不具智能”。

9. 在数学中的应用

　　 一般而言，蒙特卡罗方法在数学中用于通过生成合适的随机数（参见：随机数生成），并观察这些随机数中满足某些特定性质的比例，来求解各种问题。该方法在处理过于复杂、难以通过解析方法求解的问题时尤其有用，能够提供数值解。最常见的应用是用于蒙特卡罗积分。

积分

图
图 7：蒙特卡罗积分的原理是通过将随机点与函数值进行比较来估算积分值。

　　 确定性数值积分算法在低维度情形下表现良好，但当函数涉及多个变量时，会遇到两个主要问题：函数评估次数随着维度迅速增长。例如，在一维中进行 10 次评估可能已足够精确，但在 100 维中，则需要 $10^{100}$ 个点才能达到类似的精度——这远远超出了可计算的范围。这种现象被称为维度的诅咒。多维区域的边界可能非常复杂，以至于无法将积分问题简化为可执行的迭代积分形式。\(^\text{[96]}\) 而 “100 维” 在许多物理问题中其实并不罕见，因为在这些问题中，一个 “维度” 往往就对应于一个自由度。

图
图 8：误差以 $1/\sqrt{N}$ 的速度递减。

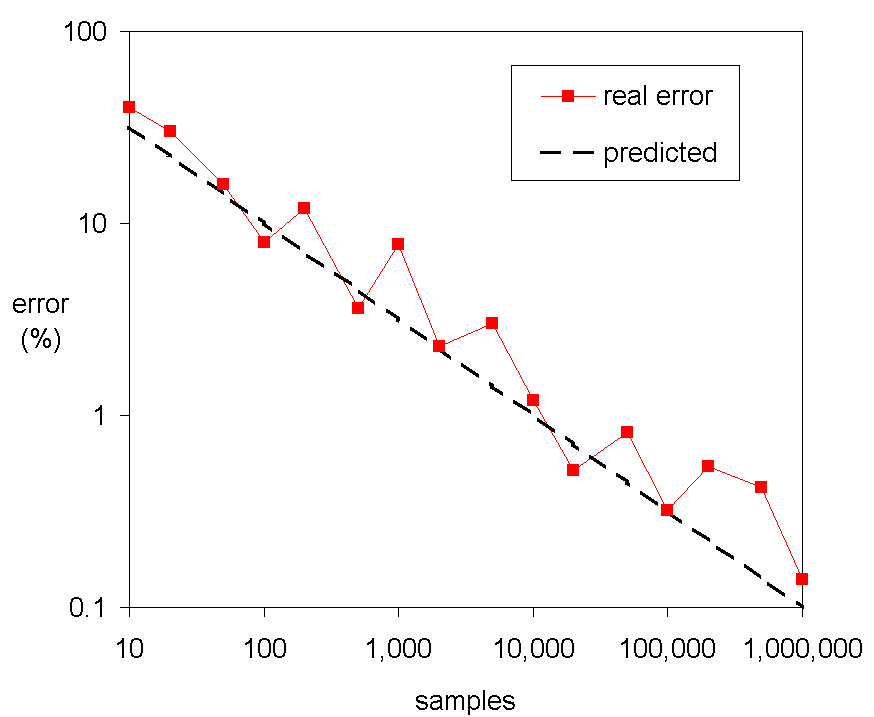
　　 蒙特卡罗方法为计算时间呈指数增长的问题提供了一种解决方案。只要目标函数具有适当的良好性质，就可以通过在 100 维空间中随机选取一些点，并对这些点处的函数值取某种形式的平均，来估算积分值。根据中心极限定理，该方法具有 $1/\sqrt{N}$ 的收敛速度——即将采样点数量增加四倍，误差会减半，而这一收敛速度与维度无关。\(^\text{[96]}\)

　　 该方法的一种改进形式称为重要性采样，其思路是：随机采样时，在被积函数较大的区域采样更频繁。为了精确地实现这一点，理论上需要预先知道积分结果，但在实际中可以通过以下方式近似实现： 用一个相似函数的积分来近似原积分；或采用一些自适应策略，例如：分层抽样，，递归分层抽样，自适应伞形采样，\(^\text{[97][98]}\)VEGAS 算法。

　　 一种类似的方法是准蒙特卡罗方法，它使用的是低偏差序列。这类序列能更均匀地 “填满” 积分区域，并更频繁地采样那些重要点，因此准蒙特卡罗方法通常能更快地收敛于积分结果。

　　 另一类在积分区域内采样的方法是模拟在该区域内的随机游走，即马尔可夫链蒙特卡罗方法。这类方法包括：Metropolis–Hastings 算法，Gibbs 采样，Wang–Landau 算法，以及一些相互作用型 MCMC 方法，如序贯蒙特卡罗采样器 \(^\text{[99]}\)。

模拟与优化

　　 另一个在数值模拟中广泛且非常强大的随机数应用场景是数值优化。该问题的目标是最小化（或最大化）某个多维向量函数。许多实际问题都可以转化为此类形式。例如：一个计算机国际象棋程序可以被看作是在尝试找出一组（比如）10 步走法，使得最终得到的评估函数值最佳；在旅行商问题中，目标是最小化总行程距离；在工程设计中也有类似的应用，如多学科设计优化。此方法还被应用于准一维模型，以高效探索大配置空间来求解粒子动力学问题。文献 \(^\text{[100]}\) 是关于模拟与优化相关多个问题的综合性综述。

　　 旅行商问题是所谓的常规优化问题：即所有用于确定最优路径所需的信息（如各目的地之间的距离）都已知且确定，目标是在所有可能路径中寻找总距离最短的那一条。但如果目标不再是最短距离，而是最少总旅行时间，问题就超出了常规优化的范畴。因为旅行时间本质上是不确定的（例如交通堵塞、出发时间等因素）。因此，若要确定最优路线，就需要不同类型的模拟：首先模拟从一个点到另一个点所需时间的可能范围（用概率分布表示而不是确定值）；然后在考虑这些不确定性的前提下，进行优化，找出最佳路径决策。

反问题

　　 将反问题进行概率化建模，可以在模型空间中定义一个概率分布。这个分布将：先验信息，与通过测量某些可观测参数（即数据）获得的新信息，结合起来，形成后验概率分布。由于在一般情况下，数据与模型参数之间的关系是非线性的，因此该后验分布可能难以表述（例如可能是多峰的、某些矩不再存在等）。

　　 在分析反问题时，仅获得最大似然解通常是不够的，人们通常还需要了解数据的分辨能力。但在通用情形下，模型参数数量可能很大，单独分析感兴趣参数的边缘概率密度变得不可行甚至无意义。解决方法是：可以根据后验概率分布伪随机地生成大量模型样本，并通过某种方式对这些模型进行分析与可视化，从而向观察者传达有关模型属性的相对可能性的信息。即使在没有显式先验分布公式的情况下，这也可以通过高效的蒙特卡罗方法实现。

　　 最著名的重要性采样方法是 Metropolis 算法。该算法可以推广，形成一种能够处理：可能高度非线性的反问题，具有复杂先验信息，并带有任意噪声分布的数据，的通用分析方法。\(^\text{[101][102]}\)

哲学层面

　　 蒙特卡罗方法的通俗化推广工作由 McCracken 推动。\(^\text{[103]}\) 其方法论层面的讨论见 Elishakoff，\(^\text{[104]}\) 以及 Grüne-Yanoff 和 Weirich。\(^\text{[105]}\)

10. 参见

11. 参考资料

引用文献

  1. Kalos 与 Whitlock，2008。
  2. Kroese, D. P.; Brereton, T.; Taimre, T.; Botev, Z. I.（2014）。《为何蒙特卡罗方法在当今如此重要》，载 *WIREs Computational Statistics*，第 6 卷第 6 期，第 386–392 页。doi:10.1002/wics.1314，S2CID: 18521840。
  3. Hubbard, Douglas；Samuelson, Douglas A.（2009 年 10 月）。《无测量的建模》，载 *OR/MS Today*，第 28–33 页。
  4. Metropolis, Nicholas；Rosenbluth, Arianna W.；Rosenbluth, Marshall N.；Teller, Augusta H.；Teller, Edward（1953 年 6 月 1 日）。《快速计算机进行状态方程计算》，载 *The Journal of Chemical Physics*，第 21 卷第 6 期，第 1087–1092 页。Bibcode:1953JChPh..21.1087M，doi:10.1063/1.1699114，ISSN 0021-9606，OSTI: 4390578，S2CID: 1046577。
  5. Hastings, W. K.（1970 年 4 月 1 日）。《利用马尔可夫链进行蒙特卡罗抽样的方法及其应用》，载 *Biometrika*，第 57 卷第 1 期，第 97–109 页。Bibcode:1970Bimka..57...97H，doi:10.1093/biomet/57.1.97，ISSN 0006-3444，S2CID: 21204149。
  6. Liu, Jun S.; Liang, Faming；Wong, Wing Hung（2000 年 3 月 1 日）。《Metropolis 采样中的多次尝试法与局部优化》，载 *Journal of the American Statistical Association*，第 95 卷第 449 期，第 121–134 页。doi:10.1080/01621459.2000.10473908，ISSN 0162-1459，S2CID: 123468109。
  7. Spall, J. C.（2003）。《通过马尔可夫链蒙特卡罗估计》，载 *IEEE Control Systems Magazine*，第 23 卷第 2 期，第 34–45 页。doi:10.1109/MCS.2003.1188770。
  8. Hill, Stacy D.; Spall, James C.（2019）。《Metropolis–Hastings 算法的平稳性与收敛性：理论视角的见解》，载 *IEEE Control Systems Magazine*，第 39 卷，第 56–67 页。doi:10.1109/MCS.2018.2876959，S2CID: 58672766。
  9. Kolokoltsov, Vassili（2010）。《非线性马尔可夫过程（Nonlinear Markov Processes）》，剑桥大学出版社，第 375 页。
  10. Del Moral, Pierre（2013）。《用于蒙特卡罗积分的平均场模拟（Mean Field Simulation for Monte Carlo Integration）》，Chapman & Hall/CRC 出版社，第 626 页。收录于 “统计与应用概率专著系列（Monographs on Statistics & Applied Probability）”。
  11. Del Moral, P.; Doucet, A.; Jasra, A.（2006）。《序贯蒙特卡罗采样器（Sequential Monte Carlo Samplers）》，载《英国皇家统计学会学报 B 系列（Journal of the Royal Statistical Society, Series B）》第 68 卷第 3 期，第 411–436 页。预印本：arXiv\:cond-mat/0212648，doi:10.1111/j.1467-9868.2006.00553.x，S2CID: 12074789。
  12. Owen, Art B.（2013）。《蒙特卡罗理论、方法与实例（Monte Carlo Theory, Methods and Examples）》(PDF)。尚在撰写中，第 15–36 页。
  13. Driels, Morris R.; Shin, Young S.（2004 年 4 月）。《确定蒙特卡罗模拟中武器效能评估所需迭代次数》，海军研究生院技术报告（2003 年 3 月至 2004 年 3 月）：第 10–11 页。
  14. Shonkwiler, R. W.; Mendivil, F.（2009）。《蒙特卡罗方法探究（Explorations in Monte Carlo Methods）》，Springer 出版社。
  15. Atanassova, E.; Gurov, T.; Karaivanova, A.; Ivanovska, S.; Durchova, M.; Dimitrov, D.（2016）。《关于 Intel MIC 架构的并行化方法研究》，载 *AIP Conference Proceedings*，第 1773 卷第 1 期：070001。Bibcode:2016AIPC.1773g0001A，doi:10.1063/1.4964983。
  16. Cunha Jr, A.; Nasser, R.; Sampaio, R.; Lopes, H.; Breitman, K.（2014）。《在云计算环境中通过蒙特卡罗方法进行不确定性量化》，载 *Computer Physics Communications*，第 185 卷第 5 期，第 1355–1363 页。arXiv:2105.09512，Bibcode:2014CoPhC.185.1355C，doi:10.1016/j.cpc.2014.01.006，S2CID: 32376269。
  17. Wei, J.; Kruis, F.E.（2013）。《一种基于 GPU 的蒙特卡罗并行方法，用于采用接受–拒绝策略的粒子凝聚模拟》，载《化学工程科学（Chemical Engineering Science）》第 104 卷，第 451–459 页。Bibcode:2013ChEnS.104..451W，doi:10.1016/j.ces.2013.08.008。
  18. Lin, Y.; Wang, F.; Liu, B.（2018）。《用于 FPGA 上大规模并行蒙特卡罗模拟的随机数生成器》，载《计算物理杂志（Journal of Computational Physics）》第 360 卷，第 93–103 页。Bibcode:2018JCoPh.360...93L，doi:10.1016/j.jcp.2018.01.029。
  19. Metropolis（1987）。
  20. Eckhardt（1987）。
  21. Mazhdrakov, Benov & Valkanov（2018），第 250 页。
  22. Haigh, Thomas；Priestley, Mark；Rope, Crispin（2014）。《洛斯阿拉莫斯押注 ENIAC：1947–1948 年的核蒙特卡罗模拟》，载《IEEE 计算史年鉴（IEEE Annals of the History of Computing）》第 36 卷第 3 期，第 42–63 页。doi:10.1109/MAHC.2014.40，S2CID: 17470931。
  23. McKean, Henry P.（1967）。《一类非线性抛物型方程的混沌传播》，载《天主教大学微分方程讲座系列（Lecture Series in Differential Equations, Catholic Univ.）》第 7 卷，第 41–57 页。
  24. McKean, Henry P.（1966）。《与非线性抛物型方程相关的一类马尔可夫过程》，载《美国国家科学院院刊（Proceedings of the National Academy of Sciences of the USA）》第 56 卷第 6 期，第 1907–1911 页。Bibcode:1966PNAS...56.1907M，doi:10.1073/pnas.56.6.1907，PMC: 220210，PMID: 16591437。
  25. Kahn, Herman；Harris, Theodore E.（1951）。《通过随机抽样估算粒子传输》（PDF），载《美国国家标准局应用数学系列（Natl. Bur. Stand. Appl. Math. Ser.）》第 12 期，第 27–30 页。
  26. Turing, Alan M.（1950）。《计算机器与智能》，载《Mind》期刊第 LIX 卷第 238 期，第 433–460 页。doi:10.1093/mind/LIX.236.433。
  27. Barricelli, Nils Aall（1954）。《进化过程的数值示例（Esempi numerici di processi di evoluzione）》，载《Methodos》，第 45–68 页。
  28. Barricelli, Nils Aall（1957）。《通过人工方法实现的共生遗传进化过程（Symbiogenetic evolution processes realized by artificial methods）》，载《Methodos》，第 143–182 页。
  29. Del Moral, Pierre（2004）。《费曼–卡克公式：谱系与相互作用粒子近似（Feynman–Kac Formulae: Genealogical and Interacting Particle Approximations）》，Springer 出版社，概率与应用系列（Probability and Its Applications），第 575 页。ISBN: 9780387202686。
  30. Del Moral, P.; Miclo, L.（2000）。《费曼–卡克公式的分支与相互作用粒子系统近似及其在非线性滤波中的应用》，载《概率研讨会 XXXIV（Séminaire de Probabilités XXXIV）》，《数学讲义丛书（Lecture Notes in Mathematics）》第 1729 卷，柏林：Springer 出版社，第 1–145 页。doi:10.1007/BFb0103798，ISBN: 978-3-540-67314-9，数学评论号（MR）1768060。
  31. Del Moral, Pierre；Miclo, Laurent（2000）。《费曼–卡克公式的 Moran 粒子系统近似》，载《随机过程及其应用（Stochastic Processes and Their Applications）》第 86 卷第 2 期，第 193–216 页。doi:10.1016/S0304-4149(99)00094-0。
  32. Del Moral, Pierre（2003）。《与薛定谔算子和费曼–卡克半群相关的李雅普诺夫指数的粒子近似》，载《ESAIM: Probability & Statistics》第 7 卷，第 171–208 页。doi:10.1051/ps:2003001。
  33. Assaraf, Roland；Caffarel, Michel；Khelif, Anatole（2000）。《固定粒子数的扩散蒙特卡罗方法》（PDF），载《物理评论 E（Phys. Rev. E）》第 61 卷第 4 期，第 4566–4575 页。Bibcode:2000PhRvE..61.4566A，doi:10.1103/physreve.61.4566，PMID: 11088257。原始 PDF 已于 2014 年 11 月 7 日存档。
  34. Caffarel, Michel；Ceperley, David；Kalos, Malvin（1993）。《关于用费曼–卡克路径积分法计算原子基态能量的评论》，载《物理评论快报（Phys. Rev. Lett.）》第 71 卷第 13 期，第 2159 页。Bibcode:1993PhRvL..71.2159C。PMID 10054598
  35. Hetherington, Jack H.（1984）。《关于矩阵的统计迭代的一些观察》，载《物理评论 A（Phys. Rev. A）》第 30 卷，第 2713–2719 页。Bibcode:1984PhRvA..30.2713H，doi:10.1103/PhysRevA.30.2713。
  36. Fermi, Enrico；Richtmyer, Robert D.（1948）。《关于蒙特卡罗计算中人口普查式抽样的简记》（PDF），LAM. 805(A)，洛斯阿拉莫斯档案馆解密报告。
  37. Rosenbluth, Marshall N.；Rosenbluth, Arianna W.（1955）。《高分子链平均伸长度的蒙特卡罗计算》，载《化学物理杂志（J. Chem. Phys.）》第 23 卷第 2 期，第 356–359 页。Bibcode:1955JChPh..23..356R，doi:10.1063/1.1741967，S2CID: 89611599。
  38. Gordon, N.J.；Salmond, D.J.；Smith, A.F.M.（1993 年 4 月）。《非线性/非高斯贝叶斯状态估计的新方法》，载《IEE Proceedings F - Radar and Signal Processing》第 140 卷第 2 期，第 107–113 页。doi:10.1049/ip-f-2.1993.0015，ISSN: 0956-375X，S2CID: 12644877。
  39. Kitagawa, G. (1996). “蒙特卡洛滤波器与非高斯非线性状态空间模型的平滑器”。《计算与图形统计期刊》，第 5 卷第 1 期，第 1–25 页。doi:10.2307/1390750。JSTOR 编号：1390750。
  40. Del Moral, Pierre (1996). “非线性滤波：相互作用粒子解法”（PDF）。《马尔可夫过程与相关领域》，第 2 卷第 4 期，第 555–580 页。原始 PDF 于 2016 年 3 月 4 日存档。检索日期：2015 年 6 月 11 日。
  41. Carvalho, Himilcon；Del Moral, Pierre；Monin, André；Salut, Gérard（1997 年 7 月）。“GPS/INS 集成中的最优非线性滤波”（PDF）。《IEEE 航空航天与电子系统汇刊》，第 33 卷第 3 期，第 835–850 页。Bibcode:1997ITAES..33..835C。doi:10.1109/7.599254。S2CID: 27966240。原始 PDF 于 2022 年 11 月 10 日存档。检索日期：2015 年 6 月 11 日。
  42. P. Del Moral, G. Rigal, 和 G. Salut.**《估计与非线性最优控制：粒子解法的统一框架》。LAAS-CNRS（土卢兹），研究报告编号：91137，DRET-DIGILOG-LAAS/CNRS 合同，1991 年 4 月。
  43. P. Del Moral, G. Rigal, 和 G. Salut.**《应用于惯性平台重定位的非线性与非高斯粒子滤波器》。LAAS-CNRS（土卢兹），研究报告编号：92207，STCAN/DIGILOG-LAAS/CNRS 协议，STCAN 编号：A.91.77.013，（94 页），1991 年 9 月。
  44. P. Del Moral, G. Rigal, 和 G. Salut.**《估计与非线性最优控制：滤波与估计中的粒子求解：实验结果》。DRET 协议编号：89.34.553.00.470.75.01，研究报告编号：2（共 54 页），1992 年 1 月。
  45. P. Del Moral, G. Rigal 和 G. Salut.**《估计与非线性最优控制：滤波与估计中的粒子求解：理论结果》。DRET 协议编号：89.34.553.00.470.75.01，研究报告编号：3（共 123 页），1992 年 10 月。
  46. P. Del Moral, J.-Ch. Noyer, G. Rigal 和 G. Salut.**《雷达信号处理中的粒子滤波：检测、估计与空中目标识别》。LAAS-CNRS（土卢兹），研究报告编号：92495，1992 年 12 月。
  47. P. Del Moral, G. Rigal 和 G. Salut.**《估计与非线性最优控制：滤波与估计中的粒子求解》。研究内容包括：滤波、最优控制与极大似然估计。DRET 协议编号：89.34.553.00.470.75.01，研究报告编号：4（共 210 页），1993 年 1 月。
  48. Pierre Del Moral（1998）.**《测度值过程与相互作用粒子系统：在非线性滤波问题中的应用》。发表于《应用概率年刊》，第 8 卷第 2 期（也见《统计与概率实验室出版物》，编号 96-15（1996）），第 438–495 页。CiteSeerX：10.1.1.55.5257。doi:10.1214/aoap/1028903535。
  49. Crisan, Dan；Gaines, Jessica；Lyons, Terry（1998）.**《分支粒子方法对 ZAKAI 方程解的收敛性》。发表于《SIAM 应用数学期刊》，第 58 卷第 5 期，第 1568–1590 页。doi:10.1137/s0036139996307371。S2CID: 39982562。
  50. Crisan, Dan；Lyons, Terry（1997）.**《非线性滤波与测度值过程》。发表于《概率论与相关领域》，第 109 卷第 2 期，第 217–244 页。doi:10.1007/s004400050131。S2CID: 119809371。
  51. Crisan, Dan；Lyons, Terry（1999）.《Kushner–Stratonovitch 方程解的粒子逼近》。发表于《概率论与相关领域》，第 115 卷第 4 期，第 549–578 页。doi:10.1007/s004400050249。S2CID: 117725141。
  52. Crisan, Dan；Del Moral, Pierre；Lyons, Terry（1999）.**《使用分支与相互作用粒子系统的离散滤波》（PDF）。发表于《马尔可夫过程与相关领域》，第 5 卷第 3 期，第 293–318 页。
  53. Del Moral, Pierre；Guionnet, Alice（1999）.**《测度值过程的稳定性及其在滤波中的应用》。发表于《巴黎科学院院报（C. R. Acad. Sci. Paris）》，第 39 卷第 1 期，第 429–434 页。
  54. Del Moral, Pierre；Guionnet, Alice（2001）.**《相互作用过程的稳定性及其在滤波与遗传算法中的应用》。发表于《亨利·庞加莱研究院年刊（Annales de l'Institut Henri Poincaré）》，第 37 卷第 2 期，第 155–194 页。Bibcode: 2001AIHPB..37..155D。doi:10.1016/s0246-0203(00)01064-5。
  55. Ripley（1987） （注：未提供完整信息，可能指 Ripley 的某部 1987 年出版的统计或图像分析方面著作）
  56. Sawilowsky（2003） （注：未提供完整信息，可能指关于统计检验或效应量的出版物）
  57. Kalos & Whitlock（2008） （注：未提供完整信息，可能是指 Kalos 和 Whitlock 合著的《Monte Carlo Methods》一书，2008 年版）
  58. Shojaeefard, M.H.; Khalkhali, A.; Yarmohammadisatri, Sadegh（2017）.《一种基于皮尔逊相关系数的高效敏感性分析方法：应用于改进几何结构的麦弗逊悬架》。发表于《车辆系统动力学》（Vehicle System Dynamics），第 55 卷第 6 期，第 827–852 页。Bibcode: 2017VSD....55..827S。doi:10.1080/00423114.2017.1283046。S2CID: 114260173。
  59. Davenport（1992） （注：未提供完整信息，可能是指某篇关于统计、时间序列或天体物理的论文）
  60. Route, Matthew（2017 年 8 月 10 日）.《射电爆发的超冷矮星种群综合研究》。发表于《天体物理学期刊》（The Astrophysical Journal），第 845 卷第 1 期，文章编号 66。arXiv:1707.02212。Bibcode: 2017ApJ...845...66R。doi:10.3847/1538-4357/aa7ede。S2CID: 118895524。
  61. Vose（2008），第 13 页。
  62. Vose（2008），第 16 页。 （注：很可能指 Vose 所著《Quantitative Risk Analysis: A Guide to Monte Carlo Simulation Modelling》一书，2008 年版）
  63. Jia, Xun；Ziegenhein, Peter；Jiang, Steve B（2014）.《基于 GPU 的高性能计算在放射治疗中的应用》。发表于《医学物理与生物学》（Physics in Medicine and Biology），第 59 卷第 4 期，R151–R182 页。Bibcode: 2014PMB....59R.151J。doi:10.1088/0031-9155/59/4/R151。PMC: 4003902。PMID: 24486639。
  64. Hill, R.；Healy, B.；Holloway, L.；Kuncic, Z.；Thwaites, D.；Baldock, C.（2014 年 3 月）.《千伏级 X 射线束剂量测量的最新进展》。发表于《医学物理与生物学》（Physics in Medicine and Biology），第 59 卷第 6 期，R183–R231 页。Bibcode: 2014PMB....59R.183H。doi:10.1088/0031-9155/59/6/R183。PMID: 24584183。S2CID: 18082594。
  65. Rogers, D.W.O.（2006）.《蒙特卡洛模拟在医学物理中的五十年》。发表于《医学物理与生物学》（Physics in Medicine and Biology），第 51 卷第 13 期，R287–R301 页。Bibcode: 2006PMB....51R.287R。doi:10.1088/0031-9155/51/13/R17。PMID: 16790908。S2CID: 12066026。
  66. Baeurle（2009） （注：未提供完整信息，可能指 Baeurle 关于多尺度建模或聚合物模拟的研究论文）
  67. Möller, W.；Eckstein, W.（1984 年 3 月 1 日）.《Tridyn —— 一种包含动态成分变化的 TRIM 模拟代码》。发表于《核仪器与方法：物理研究 B 卷——束流与材料及原子相互作用》（Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms），第 2 卷第 1 期，第 814–818 页。Bibcode: 1984NIMPB...2..814M。doi:10.1016/0168-583X(84)90321-5。
  68. MacGillivray & Dodd（1982） （注：未提供完整信息，需补充出版物名称）
  69. Golden（1979） （注：未提供完整信息，需补充出版物名称）
  70. G. A. Bird，《分子气体动力学》（Molecular Gas Dynamics），Clarendon 出版社，牛津，1976 年。
  71. Dietrich, S.；Boyd, I.（1996）.《DSMC 技术的标量优化并行实现》。发表于《计算物理学杂志》（Journal of Computational Physics），第 126 卷第 2 期，第 328–342 页。Bibcode: 1996JCoPh.126..328D。doi:10.1006/jcph.1996.0141。
  72. Chen, Shang-Ying；Hsu, Kuo-Chin；Fan, Chia-Ming（2021 年 3 月 15 日）.《广义有限差分法在随机地下水流建模中的改进》。发表于《计算物理学杂志》（Journal of Computational Physics），第 429 卷：110002。Bibcode: 2021JCoPh.42910002C。doi:10.1016/J.JCP.2020.110002。S2CID: 228828681。
  73. 《气候变化 2013：自然科学基础》（Climate Change 2013: The Physical Science Basis）（PDF）。剑桥大学出版社，2013 年，第 697 页。ISBN: 978-1-107-66182-0。检索日期：2023 年 7 月 6 日。
  74. Ojeda 等（2009） （注：未提供完整信息，需补充作者全名或文章标题以便准确翻译）
  75. Milik & Skolnick（1993） （注：未提供完整信息，需补充出版物名称）
  76. Cassey；Smith（2014）.《Ellison-Glaeser 指数置信区间的模拟》。发表于《城市经济学杂志》（Journal of Urban Economics），第 81 卷，第 93 页。doi:10.1016/j.jue.2014.02.005。
  77. Sawilowsky & Fahoome（2003） （注：未提供完整信息，可能是关于统计方法或效应量的著作，需补充标题以完成翻译）
  78. Spall, James C.（2005）.《在非常规情形下使用蒙特卡洛方法计算 Fisher 信息矩阵》。发表于《计算与图形统计期刊》（Journal of Computational and Graphical Statistics），第 14 卷第 4 期，第 889–909 页。CiteSeerX: 10.1.1.142.738。doi:10.1198/106186005X78800。S2CID: 16090098。
  79. Das, Sonjoy；Spall, James C.；Ghanem, Roger（2010）.《利用先验信息高效地用蒙特卡洛方法计算 Fisher 信息矩阵》。发表于《计算统计与数据分析》（Computational Statistics & Data Analysis），第 54 卷第 2 期，第 272–289 页。doi:10.1016/j.csda.2009.09.018。
  80. Chaslot, Guillaume；Bakkes, Sander；Szita, Istvan；Spronck, Pieter.《蒙特卡洛树搜索：一种新的游戏 AI 框架》（PDF）。来源：sander.landofsand.com，检索日期：2017 年 10 月 28 日。
  81. 《蒙特卡洛树搜索 - 关于》。原网页已于 2015 年 11 月 29 日存档。检索日期：2013 年 5 月 15 日。
  82. Chaslot, Guillaume M. J.-B；Winands, Mark H. M.；Van Den Herik, H. Jaap（2008）.《并行蒙特卡洛树搜索》。收录于《计算与游戏》（Computers and Games），《计算机科学讲义丛书》（Lecture Notes in Computer Science），第 5131 卷，第 60–71 页。CiteSeerX: 10.1.1.159.4373。doi:10.1007/978-3-540-87608-3_6。ISBN: 978-3-540-87607-6。
  83. Bruns, Pete.《Tantrix 游戏中的蒙特卡洛树搜索：Cosc490 课程期末报告》（PDF）（报告）。
  84. Silver, David；Veness, Joel.《在大型部分可观测马尔可夫决策过程（POMDP）中的蒙特卡洛规划》（PDF）。来源：0.cs.ucl.ac.uk。原 PDF 于 2016 年 7 月 18 日存档。检索日期：2017 年 10 月 28 日。
  85. Lorentz, Richard J.（2011）.《在 Havannah 游戏中改进蒙特卡洛树搜索》。收录于《计算与游戏》（Computers and Games），《计算机科学讲义丛书》（Lecture Notes in Computer Science），第 6515 卷，第 105–115 页。Bibcode: 2011LNCS.6515..105L。doi:10.1007/978-3-642-17928-0_10。ISBN: 978-3-642-17927-3。
  86. Jakl, Tomas.《Arimaa 挑战——蒙特卡洛树搜索与 Alpha-Beta 方法的对比研究》（PDF）。来源：Arimaa.com。检索日期：2017 年 10 月 28 日。
  87. Szirmay-Kalos（2008） （注：未提供完整信息，可能是关于计算机图形学或概率算法的文献，如需完整翻译请提供题目）
  88. 《海岸警卫队如何利用分析方法搜救失踪海上人员》。Dice Insights，2014 年 1 月 3 日。
  89. Stone, Lawrence D.；Kratzke, Thomas M.；Frost, John R.《美国海岸警卫队搜救最优规划系统（SAROPS）中的搜索建模与优化》（PDF）。来源：Ifremer.fr。检索日期：2017 年 10 月 28 日。
  90. 《项目风险模拟（测试版）》。网址：risk.octigo.pl。检索日期：2024 年 5 月 21 日。
  91. Carmona, René；Del Moral, Pierre；Hu, Peng；Oudjane, Nadia（2012）.《粒子方法导论及其在金融中的应用》。收录于：Carmona, René A.；Del Moral, Pierre；Hu, Peng 等（编），《金融中的数值方法》（Numerical Methods in Finance），Springer 数学会议论文集（Springer Proceedings in Mathematics），第 12 卷。柏林海德堡：施普林格出版社，第 3–49 页。CiteSeerX: 10.1.1.359.7957。doi:10.1007/978-3-642-25746-9_1。ISBN: 978-3-642-25745-2。
  92. Kroese, D. P.；Taimre, T.；Botev, Z. I.（2011）.《蒙特卡洛方法手册》（Handbook of Monte Carlo Methods）。约翰·威利父子公司（John Wiley & Sons）出版。
  93. Arenas, Daniel J.；Lett, Lanair A.；Klusaritz, Heather；Teitelman, Anne M.（2017）.《一种用于估计学生开办诊所干预措施健康与经济影响的蒙特卡洛模拟方法》。发表于《PLOS ONE》，第 12 卷第 12 期：e0189718。Bibcode: 2017PLoSO..1289718A。doi:10.1371/journal.pone.0189718。PMC: 5746244。PMID: 29284026。
  94. Elwart, Liz；Emerson, Nina；Enders, Christina；Fumia, Dani；Murphy, Kevin（2006 年 12 月）.《为低收入家庭暴力受害者增加限制令获取途径：关于拟议的家庭暴力资助项目的成本效益分析》（PDF）。威斯康星州律师协会（State Bar of Wisconsin）。原 PDF 于 2018 年 11 月 6 日存档。检索日期：2016 年 12 月 12 日。
  95. Dahlan, Hadi Akbar（2021 年 10 月 29 日）.《马来西亚与日本图书出版与定价的类型对比：基于开放数据与蒙特卡洛模拟的研究》（PDF）。发表于《马来西亚研究》（Kajian Malaysia），第 39 卷第 2 期，第 179–202 页。doi:10.21315/km2021.39.2.8。S2CID: 240435973。
  96. Press 等（1996） （注：很可能是指 Numerical Recipes 系列书籍中的某一版，如需完整翻译请提供标题）
  97. MEZEI, M（1986 年 12 月 31 日）.《自适应伞采样：非玻尔兹曼偏置的自洽确定方法》。发表于《计算物理学杂志》（Journal of Computational Physics），第 68 卷第 1 期，第 237–248 页。Bibcode: 1987JCoPh..68..237M。doi:10.1016/0021-9991(87)90054-4。
  98. Elwart, Liz；Emerson, Nina；Enders, Christina；Fumia, Dani；Murphy, Kevin（2006 年 12 月）.《为低收入家庭暴力受害者增加限制令获取途径：关于拟议的家庭暴力资助项目的成本效益分析》（PDF）。威斯康星州律师协会（State Bar of Wisconsin）。原 PDF 于 2018 年 11 月 6 日存档。检索日期：2016 年 12 月 12 日。
  99. Dahlan, Hadi Akbar（2021 年 10 月 29 日）.《马来西亚与日本图书出版与定价的类型对比：基于开放数据与蒙特卡洛模拟的研究》（PDF）。发表于《马来西亚研究》（Kajian Malaysia），第 39 卷第 2 期，第 179–202 页。doi:10.21315/km2021.39.2.8。S2CID: 240435973。
  100. Press 等（1996） （注：很可能是指 Numerical Recipes 系列书籍中的某一版，如需完整翻译请提供标题）
  101. MEZEI, M（1986 年 12 月 31 日）.《自适应伞采样：非玻尔兹曼偏置的自洽确定方法》。发表于《计算物理学杂志》（Journal of Computational Physics），第 68 卷第 1 期，第 237–248 页。Bibcode: 1987JCoPh..68..237M。doi:10.1016/0021-9991(87)90054-4。
  102. 塔朗托拉（2005）
  103. McCracken, D. D.（1955）.《蒙特卡洛方法》。发表于《科学美国人》（Scientific American），第 192 卷第 5 期，第 90–97 页。
  104. Elishakoff, I.（2003）.《关于蒙特卡洛方法哲学的笔记》。发表于《应用力学国际期刊》（International Applied Mechanics），第 39 卷第 7 期，第 753–762 页。
  105. Grüne-Yanoff, T.；Weirich, P.（2010）.《模拟的哲学与认识论：综述》。发表于《模拟与博弈》（Simulation & Gaming），第 41 卷第 1 期，第 20–50 页。

资料来源


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利