量子引力（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：cGh 立方体的图示
图
图 2：“以维恩图表示”

　　 量子引力（QG）是理论物理学的一个领域，旨在根据量子力学的原理描述引力。它处理的是在引力效应和量子效应都不能忽视的环境下的问题，如黑洞或类似的紧凑天体附近，以及宇宙大爆炸后早期阶段的时空。[1][2]

　　 自然界的四种基本相互作用中，除了引力，其他三种相互作用——电磁相互作用、强相互作用和弱相互作用——已经在量子力学和量子场论的框架中得到了描述。引力是唯一尚未完全适应量子力学框架的相互作用。当前对引力的理解基于阿尔伯特·爱因斯坦的广义相对论，这一理论结合了特殊相对论，并深刻修改了时间和空间等概念的理解。虽然广义相对论因其优雅和精确性受到高度评价，但它也有其局限性：例如，黑洞内部的引力奇点、暗物质的假设以及暗能量和宇宙常数的关系，这些都是目前关于引力未解之谜之一，[3] 这些都表明广义相对论在不同尺度上的崩溃，并突显了需要一种能够进入量子领域的引力理论。在接近普朗克长度的尺度上，如黑洞中心附近，时空的量子波动预计会发挥重要作用。[4] 最后，真空能量的预测值与观测值之间的差异（根据考虑的不同，差异可能达到 60 或 120 个数量级）[5][6] 强调了量子引力理论的必要性。

　　 量子引力领域正在积极发展，理论学者正在探索多种解决量子引力问题的方法，其中最受欢迎的是 M 理论和环量子引力。[7] 所有这些方法都旨在描述引力场的量子行为，尽管这并不一定包括将所有基本相互作用统一成一个单一的数学框架。然而，许多量子引力的途径，如弦理论，试图开发一个描述所有基本相互作用的框架。这样的理论通常被称为 “万物理论”。一些方法，如环量子引力，并不试图做出这种统一尝试；相反，它们努力量子化引力场，同时将引力与其他相互作用分开。其他一些较不为人知，但同样重要的理论包括因果动力学三角化、非交换几何和扭曲理论。[8]

　　 制定量子引力理论的一个难点是，量子引力效应的直接观测预计只会在接近普朗克尺度（约 10^-35 米）的长度尺度上出现，这一尺度远小于目前高能粒子加速器所能达到的能量水平，因此，物理学家缺乏实验数据来区分已提出的竞争性理论。[n.b. 1][n.b. 2]

　　 已提出了一些思维实验的方法，作为测试量子引力理论的工具。[9][10] 在量子引力领域有若干悬而未决的问题——例如，尚不清楚基本粒子的自旋如何源引力，思维实验可能为探索这些问题的可能解决方案提供路径，[11] 即使没有实验室实验或物理观察。

　　 21 世纪初，出现了新的实验设计和技术，这些技术表明，间接测试量子引力的方法在未来几十年内可能成为可行的。[12][13][14][15] 这一研究领域被称为现象学量子引力。

1. 概述

图
图 3：图示展示量子引力在物理学理论层级中的位置

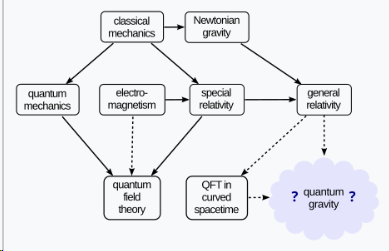
　　 将这些理论在所有能量尺度上结合起来的困难，主要来自于这些理论对宇宙运作方式的不同假设。广义相对论将引力建模为时空的弯曲：用约翰·阿奇博尔德·惠勒的话来说，“时空告诉物质如何运动；物质告诉时空如何弯曲。” 另一方面，量子场论通常是在特殊相对论中使用的平直时空中进行表述的。目前没有任何理论能够成功地描述物质动力学（用量子力学建模）如何影响时空的弯曲的普遍情况。如果试图将引力视为另一种量子场，得到的理论就无法进行重整化。即便是在时空弯曲事先固定的简单情况下，发展量子场论也变得更加数学上具有挑战性，许多物理学家在平直时空中使用的量子场论思想不再适用。

　　 人们普遍希望量子引力理论能够帮助我们理解非常高能和非常小空间尺度上的问题，例如黑洞的行为以及宇宙的起源。

　　 一个主要的障碍是，在具有固定度规的弯曲时空中，量子场论中的玻色子/费米子算符场对于时空分离的点是超对易的。（这是一种施加局部性的原则。）然而，在量子引力中，度规是动态的，因此两个点是否时空分离取决于状态。实际上，它们可以处于量子叠加态，既是时空分离的，也不是时空分离的。

2. 量子力学与广义相对论

引力子

　　 观察到除了引力以外的所有基本力都有一个或多个已知的媒介粒子，这使得研究人员认为引力也应该有一个类似的粒子。这个假想的粒子被称为引力子。引力子作为一种力的粒子，类似于电磁相互作用中的光子。在一些温和的假设下，广义相对论的结构要求它们遵循量子力学描述，即相互作用的理论自旋为 2 的无质量粒子。[19][20][21][22][23] 自 1970 年代以来，物理学的统一理论中许多公认的观点假设并在某种程度上依赖于引力子的存在。韦因伯格–维滕定理对引力子作为复合粒子的理论提出了一些约束。[24][25] 虽然引力子是量子引力描述中的一个重要理论步骤，但普遍认为它们无法被探测，因为它们的相互作用太弱。[26]

引力的非重整化性

　　 广义相对论像电磁学一样，是一个经典场论。人们可能期望，像电磁学一样，引力也应该有一个对应的量子场论。

　　 然而，引力是扰动非重整化的。[27][28] 为了使量子场论根据这种理解具有良好的定义，它必须是渐近自由的或渐近安全的。理论必须通过选择有限数量的参数来表征，这些参数理论上可以通过实验确定。例如，在量子电动力学中，这些参数是电子的电荷和质量，且在特定能量尺度下可以测量。

　　 另一方面，在量子化引力时，扰动理论中需要无穷多个独立的参数（反常项系数）来定义理论。对于给定的这些参数的选择，我们可以理解该理论，但由于不可能进行无限次实验来确定每个参数的值，因此有人认为在扰动理论中我们没有一个有意义的物理理论。在低能量下，重整化群的逻辑告诉我们，尽管这些无穷多个参数的选择未知，量子引力会退化为通常的爱因斯坦广义相对论理论。另一方面，如果我们能够探测非常高的能量，在量子效应占主导的情况下，那么所有这些无穷多个未知参数都会开始变得重要，这时我们将无法做出任何预测。[29]

　　 可以设想，在正确的量子引力理论中，这些无穷多个未知参数将会缩减为一个有限的参数集，并且这些参数可以被测量。一个可能性是，常规的扰动理论并不是判断理论是否重整化的可靠指南，实际上引力可能存在一个紫外固定点。由于这是一个非扰动量子场论的问题，找到一个可靠的答案是非常困难的，且正在通过渐近安全性计划进行研究。另一个可能性是，存在一些新的、尚未发现的对称性原则，这些原则约束了参数，并将其简化为一个有限的集合。这是弦理论所采取的路径，在弦理论中，弦的所有激发基本上表现为新的对称性。[30][需要更好的来源]

量子引力作为一种有效场论

　　 在有效场论中，非重整化理论中的无穷多个参数中，只有最前面的几个参数被巨大的能量尺度压制，因此在计算低能量效应时可以忽略它们。因此，至少在低能量范围内，这个模型是一个具有预测能力的量子场论。[31] 此外，许多理论学家认为标准模型本身也应被视为一种有效场论，其中 “非重整化” 相互作用被大的能量尺度压制，且其效应因此没有在实验中被观察到。[32]

　　 通过将广义相对论视为一种有效场论，实际上可以对量子引力做出合法的预测，至少对于低能量现象是如此。一个例子是著名的计算，即在两个质量之间的经典牛顿引力势中，微小的第一阶量子力学修正。[31] 另一个例子是对贝肯斯坦-霍金熵公式的修正计算。[33][34]

时空背景依赖性

　　 广义相对论的一个基本教训是，没有像牛顿力学和特殊相对论中那样固定的时空背景；时空几何是动态的。虽然原则上易于理解，但这是一个复杂的概念，理解广义相对论时必须考虑这个问题，其后果深远，甚至在经典层面上都没有得到完全探索。从某种程度上讲，广义相对论可以被看作是一个关系论的理论，[35] 其中唯一具有物理意义的信息是时空中不同事件之间的关系。

　　 另一方面，量子力学自其创立以来，一直依赖于固定的背景（非动态）结构。在量子力学中，时间是给定的且不是动态的，就像在牛顿经典力学中一样。在相对论性量子场论中，就像在经典场论中一样，闵可夫斯基时空是该理论的固定背景。

　　 弦理论

图
图 4：亚原子世界中的相互作用：标准模型中点状粒子的世界线或弦理论中闭合弦扫过的世界表面

　　 弦理论可以被视为量子场论的一种推广，在这种理论中，取代了点粒子的是弦状物体，它们在固定的时空背景中传播，尽管闭弦之间的相互作用以动态的方式产生了时空。虽然弦理论最初起源于夸克禁闭的研究，而不是量子引力的研究，但很快就发现弦的谱包含了引力子，并且弦的某些振动模式的 “凝聚” 相当于对原始背景的修改。从这个意义上说，弦的微扰理论表现出了微扰理论应有的特征，这种微扰理论可能表现出对渐近行为的强烈依赖（例如，在 AdS/CFT 对偶性中看到的那样），而这是一种弱的背景依赖性形式。

　　 背景无关理论

　　 环量子引力是努力构建背景无关量子理论的成果。

　　 拓扑量子场理论提供了一个背景无关量子理论的例子，但它没有局部自由度，并且只有有限的全局自由度。这不足以描述 3+1 维中的引力，因为根据广义相对论，引力具有局部自由度。然而，在 2+1 维中，引力是一个拓扑场理论，并且已成功以几种不同的方式量子化，包括自旋网络。[citation needed]

半经典量子引力

　　 主条目：弯曲时空中的量子场论和半经典引力 在弯曲（非闵可夫斯基）背景下的量子场论，尽管还不是完整的量子引力理论，但已经显示出许多有希望的早期结果。类似于 20 世纪早期量子电动力学的发展（当时物理学家在经典电磁场中考虑量子力学），在弯曲背景下考虑量子场论已导致一些预测，如黑洞辐射。

　　 诸如 Unruh 效应（在某些加速参考系中存在粒子，而在静止参考系中没有）等现象，在考虑弯曲背景时并不会造成任何困难（即使在平坦的闵可夫斯基背景下，Unruh 效应也会发生）。真空态是能量最小的状态（可能包含也可能不包含粒子）。

时间问题

　　 将量子力学与广义相对论结合时出现的一个概念性困难来自于这两种框架中时间的作用截然不同。在量子理论中，时间作为一个独立的背景，量子态通过时间演化，哈密顿算符作为量子态在时间中微小平移的生成算符。[36] 相反，广义相对论将时间视为一个动态变量，直接与物质相关，并且要求哈密顿约束消失。[37] 由于这种时间的可变性已在宏观尺度上被观察到，它排除了在宏观层面上使用固定的时间概念的可能性，这类似于量子理论中的时间观念。

3. 候选理论

　　 目前存在多种提出的量子引力理论。[38] 然而，目前仍没有完整且一致的量子引力理论，这些候选模型仍需克服重大的形式和概念性问题。此外，它们还面临一个共同的问题：尚无办法通过实验验证量子引力的预测。不过，随着未来来自宇宙学观测和粒子物理实验的数据逐步获得，人们对这一情况的改变充满希望。[39][40]

弦理论

图
图 5：卡拉比–丘流形的投影图，这是弦理论中对额外维度进行压缩的一种方法。

　　 弦理论的核心思想是将量子场论中经典的点粒子概念替换为一种描述一维延展物体的量子理论，即弦理论。[41] 在目前实验可达到的能量水平下，这些弦与点状粒子无法区分，但关键在于，同一种基本弦的不同振动模式会表现为具有不同（电荷或其他）性质的粒子。通过这种方式，弦理论有望成为对所有粒子和相互作用的统一描述。[42] 这一理论的一个成功之处在于，其中总会有一种模式对应于引力子的存在——即引力的传递粒子；然而，这一成功的代价是引入了一些非同寻常的特性，比如除了常规的三维空间和一维时间外，还需要额外的六个空间维度。[43]

　　 在所谓的 “第二次超弦革命” 中，人们推测，弦理论与一种被称为超引力的广义相对论和超对称性统一理论共同构成了一个假设的十一维模型，即 M 理论。这一理论可能成为一个独特且一致的量子引力理论。[45][46] 然而，按照目前的理解，弦理论允许一个非常庞大的（据估计多达 \(10^{500}\) 个）一致真空解的集合，被称为 “弦景观”。在这一庞大解集中进行筛选和分类仍是一个重大挑战。

圈量子引力

图
图 6：圈量子引力中使用的简单旋量网络

　　 圈量子引力严肃地考虑了广义相对论的见解，即时空是一个动态场，因此也是一个量子对象。其第二个核心思想是，量子的不连续性（这种不连续性决定了其他场论中类似粒子的行为，例如电磁场中的光子）同样会影响空间的结构。

　　 圈量子引力的主要成果是推导出了在普朗克长度处空间的颗粒化结构。这一结果基于以下考虑：对于电磁学，代表场中每个频率能量的量子算符具有离散的谱，因此每个频率的能量是量子化的，其量子就是光子。对于引力，代表每个表面或空间区域的面积和体积的算符同样具有离散谱。因此，任何空间区域的面积和体积也是量子化的，其量子是基本的空间量子。由此可知，时空在普朗克尺度具有基本的量子颗粒结构，这一结构切断了量子场论的紫外发散问题。

　　 时空的量子态通过一种称为旋量网络的数学结构来描述。旋量网络最初由罗杰·彭罗斯以抽象形式引入，后来由卡洛·罗韦利和李·斯莫林证明可以从广义相对论的非微扰量子化自然推导出来。旋量网络并不表示时空中某个场的量子态，而是直接表示时空的量子态。

　　 该理论基于广义相对论的一种重新表述，即阿什特卡变量，这种表述使用电场和磁场的数学类比来表示几何引力。[47][48] 在量子理论中，空间被表示为一种称为旋量网络的网络结构，其随着时间以离散步骤演化。[49][50][51][52]

　　 该理论的动力学目前有多种版本。一种版本从广义相对论的正则量子化出发，其类似于薛定谔方程的形式是惠勒–德威特方程，可以在该理论中定义。[53] 在协变（或旋泡）表述中，量子动力学通过对离散形式的时空（称为旋泡）的求和得到。这些旋泡表示旋量网络的历史演化。

其他理论

　　 在量子引力研究中，还有许多其他的方法。这些理论根据广义相对论和量子理论的不同特点决定哪些保持不变，哪些需要修改。[54][55] 以下是一些示例：

4. 实验测试

　　 正如上文所强调的，量子引力效应极其微弱，因此难以测试。这一原因导致在 1990 年代末之前，实验测试量子引力的可能性并未受到太多关注。然而，自 2000 年代起，物理学家意识到，量子引力效应的证据可以为理论发展提供指导。由于理论发展较为缓慢，研究实验测试可能性的现象学量子引力领域开始受到更多关注。[61]

　　 量子引力现象学中最广泛研究的可能性包括：通过引力介导的纠缠现象探测量子引力效应，[62][63] 洛伦兹不变性的违反，宇宙微波背景辐射（特别是其偏振）中量子引力效应的印记，空间泡沫波动引起的退相干。[64][65][66][67]

　　 后者的情况通过伽马射线暴光子以及天体和大气中中微子的观测进行搜索，从而对量子引力参数设定了限制。[68][69][70]

　　 欧洲航天局的 INTEGRAL 卫星测量了不同波长光子的偏振情况，能够将空间粒度的上限限制在小于 \(10^{-48} \, \text{m}\)，即比普朗克尺度低 13 个数量级。[71][72][需要更可靠的来源]

　　 BICEP2 实验最初检测到可能由早期宇宙中的引力波引起的原初 B 模偏振。若这一信号确实源自原初效应，则可能是量子引力效应的指示。然而，很快发现该偏振实际上是由于星际尘埃干扰引起的。[73]

5. 参见

6. 注释

  1. 早期宇宙中的量子效应可能对当前宇宙结构产生可观测的影响，例如引力可能在其他力的统一中发挥作用。参见上述 Wald 引用的文献。
  2. 关于时空几何的量子化，另请参见普朗克长度条目中的相关示例。

7. 参考文献

　　 1. Rovelli, Carlo (2008). "Quantum gravity". *Scholarpedia*. 3 (5): 7117. Bibcode:2008SchpJ...3.7117R. doi:10.4249/scholarpedia.7117.
2. Kiefer, Claus (2012). *Quantum gravity*. International series of monographs on physics (3rd ed.). Oxford: Oxford University Press. pp. 1–4. ISBN 978-0-19-958520-5.
3. Mannheim, Philip (2006). "Alternatives to dark matter and dark energy". *Progress in Particle and Nuclear Physics*. 56 (2): 340–445. arXiv:astro-ph/0505266. Bibcode:2006PrPNP..56..340M. doi:10.1016/j.ppnp.2005.08.001. S2CID 14024934.
4. Nadis, Steve (2 December 2019). "Black Hole Singularities Are as Inescapable as Expected". *quantamagazine.org*. *Quanta Magazine*. Archived from the original on 14 April 2020. Retrieved 22 April 2020.
5. Bousso, Raphael (2008). "The cosmological constant". *General Relativity and Gravitation*. 40 (2–3): 607–637. arXiv:0708.4231. Bibcode:2008GReGr..40..607B. doi:10.1007/s10714-007-0557-5.
6. Lea, Rob (2021). "A new generation takes on the cosmological constant". *Physics World*. 34 (3): 42. Bibcode:2021PhyW...34c..42L. doi:10.1088/2058-7058/34/03/32.
7. Penrose, Roger (2007). *The road to reality: a complete guide to the laws of the universe*. Vintage. p. 1017. ISBN 9780679776314. OCLC 716437154.
8. Rovelli, Carlo (2001). "Notes for a brief history of quantum gravity". arXiv:gr-qc/0006061.
9. Lindner, Nethanel H.; Peres, Asher (2005). "Testing quantum superpositions of the gravitational field with Bose-Einstein condensates". *Physical Review A*. 71 (2): 024101. arXiv:gr-qc/0410030. doi:10.1103/PhysRevA.71.024101.
10. Kafri, Dvir; Taylor, Jacob M (2013). "A noise inequality for classical forces". arXiv:1311.4558 [quant-ph].
11. Nemirovsky, J.; Cohen, E.; Kaminer, I. (5 November 2021). "Spin Spacetime Censorship". *Annalen der Physik*. 534 (1). arXiv:1812.11450. doi:10.1002/andp.202100348. S2CID 119342861.
12. Hossenfelder, Sabine (2 February 2017). "What Quantum Gravity Needs Is More Experiments". *Nautilus*. Archived from the original on 28 January 2018. Retrieved 21 September 2020.
13. *Experimental search for quantum gravity*. Cham: Springer. 2017. ISBN 9783319645360.
14. Carney, Daniel; Stamp, Philip C. E.; Taylor, Jacob M. (7 February 2019). "Tabletop experiments for quantum gravity: a user's manual". *Classical and Quantum Gravity*. 36 (3): 034001. arXiv:1807.11494. Bibcode:2019CQGra..36c4001C. doi:10.1088/1361-6382/aaf9ca. S2CID 119073215.
15. Danielson, Daine L.; Satishchandran, Gautam; Wald, Robert M. (2022-04-05). "Gravitationally mediated entanglement: Newtonian field versus gravitons". *Physical Review D*. 105 (8): 086001. arXiv:2112.10798. Bibcode:2022PhRvD.105h6001D. doi:10.1103/PhysRevD.105.086001. S2CID 245353748. Archived from the original on 2023-01-22. Retrieved 2022-12-11.
16. Wheeler, John Archibald (2010). *Geons, Black Holes, and Quantum Foam: A Life in Physics*. W. W. Norton & Company. p. 235. ISBN 9780393079487.
17. Zee, Anthony (2010). *Quantum Field Theory in a Nutshell* (second ed.). Princeton University Press. pp. 172, 434–435. ISBN 978-0-691-14034-6. OCLC 659549695.
18. Wald, Robert M. (1994). *Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics*. University of Chicago Press. ISBN 978-0-226-87027-4.
19. Kraichnan, R. H. (1955). "Special-Relativistic Derivation of Generally Covariant Gravitation Theory". *Physical Review*. 98 (4): 1118–1122. Bibcode:1955PhRv...98.1118K. doi:10.1103/PhysRev.98.1118.
20. Gupta, S. N. (1954). "Gravitation and Electromagnetism". *Physical Review*. 96 (6): 1683–1685. Bibcode:1954PhRv...96.1683G. doi:10.1103/PhysRev.96.1683.
21. Gupta, S. N. (1957). "Einstein's and Other Theories of Gravitation". *Reviews of Modern Physics*. 29 (3): 334–336. Bibcode:1957RvMP...29..334G. doi:10.1103/RevModPhys.29.334.
22. Gupta, S. N. (1962). "Quantum Theory of Gravitation". *Recent Developments in General Relativity*. Pergamon Press. pp. 251–258.
23. Deser, S. (1970). "Self-Interaction and Gauge Invariance". *General Relativity and Gravitation*. 1 (1): 9–18. arXiv:gr-qc/0411023. Bibcode:1970GReGr...1....9D. doi:10.1007/BF00759198. S2CID 14295121.
24. Weinberg, Steven; Witten, Edward (1980). "Limits on massless particles". *Physics Letters B*. 96 (1–2): 59–62. Bibcode:1980PhLB...96...59W. doi:10.1016/0370-2693(80)90212-9.
25. Horowitz, Gary T.; Polchinski, Joseph (2006). "Gauge/gravity duality". In Oriti, Daniele (ed.). *Approaches to Quantum Gravity*. Cambridge University Press. arXiv:gr-qc/0602037. Bibcode:2006gr.qc.....2037H. ISBN 9780511575549. OCLC 873715753.
26. Rothman, Tony; Boughn, Stephen (2006). "Can Gravitons be Detected?". *Foundations of Physics*. 36 (12): 1801–1825. arXiv:gr-qc/0601043. Bibcode:2006FoPh...36.1801R. doi:10.1007/s10701-006-9081-9. S2CID 14008778. Archived from the original on 2020-08-06. Retrieved 2020-05-15.
27. Feynman, Richard P. (1995). *Feynman Lectures on Gravitation*. Reading, Massachusetts: Addison-Wesley. pp. xxxvi–xxxviii, 211–212. ISBN 978-0201627343.
28. Hamber, H. W. (2009). *Quantum Gravitation – The Feynman Path Integral Approach*. Springer Nature. ISBN 978-3-540-85292-6. 29. Goroff, Marc H.; Sagnotti, Augusto (1985). "Quantum gravity at two loops". *Physics Letters B*. 160 (1–3): 81–86. Bibcode:1985PhLB..160...81G. doi:10.1016/0370-2693(85)91470-4.
30. Distler, Jacques (2005-09-01). "Motivation". golem.ph.utexas.edu. Archived from the original on 2019-02-11. Retrieved 2018-02-24.
31. Donoghue, John F. (1995). "Introduction to the Effective Field Theory Description of Gravity". In Cornet, Fernando (ed.). *Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 June–1 July 1995*. Singapore: World Scientific. arXiv:gr-qc/9512024. Bibcode:1995gr.qc....12024D. ISBN 978-981-02-2908-5.
32. Zinn-Justin, Jean (2007). *Phase transitions and renormalization group*. Oxford: Oxford University Press. ISBN 9780199665167. OCLC 255563633.
33. Calmet, Xavier; Kuipers, Folkert (2021). "Quantum gravitational corrections to the entropy of a Schwarzschild black hole". *Phys. Rev. D*. 104 (6): 6. arXiv:2108.06824. Bibcode:2021PhRvD.104f6012C. doi:10.1103/PhysRevD.104.066012. S2CID 237091145.
34. Campos Delgado, Ruben (2022). "Quantum gravitational corrections to the entropy of a Reissner-Nordström black hole". *Eur. Phys. J. C*. 82 (3): 272. arXiv:2201.08293. Bibcode:2022EPJC...82..272C. doi:10.1140/epjc/s10052-022-10232-0. S2CID 247824137.
35. Smolin, Lee (2001). *Three Roads to Quantum Gravity*. Basic Books. pp. 20–25. ISBN 978-0-465-07835-6. Pages 220–226 are annotated references and guide for further reading.
36. Sakurai, J. J.; Napolitano, Jim J. (2010-07-14). *Modern Quantum Mechanics* (2 ed.). Pearson. p. 68. ISBN 978-0-8053-8291-4.
37. Novello, Mario; Bergliaffa, Santiago E. (2003-06-11). *Cosmology and Gravitation: Xth Brazilian School of Cosmology and Gravitation; 25th Anniversary (1977–2002), Mangaratiba, Rio de Janeiro, Brazil*. Springer Science & Business Media. p. 95. ISBN 978-0-7354-0131-0.
38. A timeline and overview can be found in Rovelli, Carlo (2000). "Notes for a brief history of quantum gravity". arXiv:gr-qc/0006061. (verify against ISBN 9789812777386).
39. Ashtekar, Abhay (2007). *Loop Quantum Gravity: Four Recent Advances and a Dozen Frequently Asked Questions*. The Eleventh Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity. p. 126. arXiv:0705.2222. Bibcode:2008mgm..conf..126A. doi:10.1142/9789812834300_0008. ISBN 978-981-283-426-3. S2CID 119663169.
40.Schwarz, John H. (2007). "String Theory: Progress and Problems". *Progress of Theoretical Physics Supplement*. 170: 214–226. arXiv:hep-th/0702219. Bibcode:2007PThPS.170..214S. doi:10.1143/PTPS.170.214. S2CID 16762545.
41.本科生级别易于理解的弦理论入门书籍可以参考： Zwiebach, Barton (2004). *A First Course in String Theory*. Cambridge University Press. ISBN 978-0-521-83143-7。 更全面的综述书籍包括： Polchinski, Joseph (1998). *String Theory Vol. I: An Introduction to the Bosonic String*. Cambridge University Press. ISBN 978-0-521-63303-1。 Polchinski, Joseph (1998b). *String Theory Vol. II: Superstring Theory and Beyond*. Cambridge University Press. ISBN 978-0-521-63304-8。
42.Ibanez, L. E. (2000). *“The second string (phenomenology) revolution”*. *Classical and Quantum Gravity*. 17 (5): 1117–1128. [arXiv:hep-ph/9911499](https://arxiv.org/abs/hep-ph/9911499). Bibcode: 2000CQGra..17.1117I. doi:10.1088/0264-9381/17/5/321. S2CID: 15707877.
43.关于引力子作为弦谱的一部分，可参见 **Green, Schwarz & Witten 2012**，第 2.3 和 5.3 节；关于额外维度，参见第 4.2 节。
44.Weinberg, Steven (2000). *“Chapter 31”*. *The Quantum Theory of Fields II: Modern Applications*. Cambridge University Press. ISBN: 978-0-521-55002-4.
45.Townsend, Paul K. (1996). *“Four Lectures on M-Theory”*. *High Energy Physics and Cosmology*. ICTP Series in Theoretical Physics. 13: 385. [arXiv:hep-th/9612121](https://arxiv.org/abs/hep-th/9612121). Bibcode: 1997hepcbconf..385T.
46.Duff, Michael (1996). *“M-Theory (the Theory Formerly Known as Strings)”*. *International Journal of Modern Physics A*. 11 (32): 5623–5642. [arXiv:hep-th/9608117](https://arxiv.org/abs/hep-th/9608117). Bibcode: 1996IJMPA..11.5623D. doi:10.1142/S0217751X96002583. S2CID: 17432791.
47.Ashtekar, Abhay (1986). *“New variables for classical and quantum gravity”*. *Physical Review Letters*. 57 (18): 2244–2247. Bibcode: 1986PhRvL..57.2244A. doi:10.1103/PhysRevLett.57.2244. PMID: 10033673.
48.Ashtekar, Abhay (1987). *“New Hamiltonian formulation of general relativity”*. *Physical Review D*. 36 (6): 1587–1602. Bibcode: 1987PhRvD..36.1587A. doi:10.1103/PhysRevD.36.1587. PMID: 9958340.
49.Thiemann, Thomas (2007). *“Loop Quantum Gravity: An Inside View”*. In *Approaches to Fundamental Physics*. *Lecture Notes in Physics*. Vol. 721. pp. 185–263. [arXiv:hep-th/0608210](https://arxiv.org/abs/hep-th/0608210). Bibcode: 2007LNP...721..185T. doi:10.1007/978-3-540-71117-9_10. ISBN: 978-3-540-71115-5. S2CID: 119572847.
50.Rovelli, Carlo (1998). *“Loop Quantum Gravity”*. *Living Reviews in Relativity*. 1 (1): 1. [arXiv:gr-qc/9710008](https://arxiv.org/abs/gr-qc/9710008). Bibcode: 1998LRR.....1....1R. doi:10.12942/lrr-1998-1. PMC: 5567241. PMID: 28937180.
51.Ashtekar, Abhay; Lewandowski, Jerzy (2004). *“Background Independent Quantum Gravity: A Status Report”*. *Classical and Quantum Gravity*. 21 (15): R53–R152. [arXiv:gr-qc/0404018](https://arxiv.org/abs/gr-qc/0404018). Bibcode: 2004CQGra..21R..53A. doi:10.1088/0264-9381/21/15/R01. S2CID: 119175535.
52.Thiemann, Thomas (2003). *“Lectures on Loop Quantum Gravity”*. In *Quantum Gravity*. *Lecture Notes in Physics*. Vol. 631. pp. 41–135. [arXiv:gr-qc/0210094](https://arxiv.org/abs/gr-qc/0210094). Bibcode: 2003LNP...631...41T. doi:10.1007/978-3-540-45230-0_3. ISBN: 978-3-540-40810-9. S2CID: 119151491.
53.Rovelli, Carlo (2004). *Quantum Gravity*. Cambridge University Press. ISBN: 978-0-521-71596-6.
54.Isham, Christopher J. (1994). *“Prima facie questions in quantum gravity”*. In *Ehlers, Jürgen; Friedrich, Helmut (eds.)*. *Canonical Gravity: From Classical to Quantum*. *Lecture Notes in Physics*. Vol. 434. Springer. pp. 1–21. [arXiv:gr-qc/9310031](https://arxiv.org/abs/gr-qc/9310031). Bibcode: 1994LNP...434....1I. doi:10.1007/3-540-58339-4_13. ISBN 978-3-540-58339-4. S2CID 119364176.
55.Sorkin, Rafael D. (1997). *“Forks in the Road, on the Way to Quantum Gravity”*. *International Journal of Theoretical Physics*. 36 (12): 2759–2781. [arXiv:gr-qc/9706002](https://arxiv.org/abs/gr-qc/9706002). Bibcode: 1997IJTP...36.2759S. doi:10.1007/BF02435709. S2CID 4803804.
56.Klimets, A. P. (2017). *“Philosophy Documentation Center, Western University – Canada”*. (PDF). *Philosophy Documentation Center, Western University – Canada*. pp. 25–32. Archived (PDF) from the original on 2019-07-01. Retrieved 2020-04-24.
57.A.P. Klimets (2023). *Quantum Gravity*. *Current Research in Statistics & Mathematics*, 2(1), 141–155.
58.Loll, Renate (1998). *“Discrete Approaches to Quantum Gravity in Four Dimensions”*. *Living Reviews in Relativity*. 1 (1): 13. [arXiv:gr-qc/9805049](https://arxiv.org/abs/gr-qc/9805049). Bibcode: 1998LRR.....1...13L. doi:10.12942/lrr-1998-13. PMC 5253799. PMID 28191826. 59.Hawking, Stephen W. (1987). *“Quantum cosmology”*. In *Hawking, Stephen W.; Israel, Werner (eds.)*. *300 Years of Gravitation*. Cambridge University Press. pp. 631–651. ISBN 978-0-521-37976-2.
60.See ch. 33 in Penrose 2005 and references therein.
61.Hossenfelder, Sabine (2011). *“Experimental Search for Quantum Gravity”*. In *Frignanni, V. R. (ed.)*. *Classical and Quantum Gravity: Theory, Analysis and Applications*. Nova Publishers. ISBN 978-1-61122-957-8. Archived from the original on 2017-07-01. Retrieved 2012-04-01.
62.Lindner, Nethanel H.; Peres, Asher (2005). *“Testing quantum superpositions of the gravitational field with Bose-Einstein condensates”*. *Physical Review A*. 71 (2): 024101. [arXiv:gr-qc/0410030](https://arxiv.org/abs/gr-qc/0410030). doi:10.1103/PhysRevA.71.024101.
63.Kafri, Dvir; Taylor, Jacob M. (2013). *“A noise inequality for classical forces”*. [arXiv:1311.4558](https://arxiv.org/abs/1311.4558) [quant-ph].
64.Oniga, Teodora; Wang, Charles H.-T. (2016-02-09). *“Quantum gravitational decoherence of light and matter”*. *Physical Review D*. 93 (4): 044027. [arXiv:1511.06678](https://arxiv.org/abs/1511.06678). Bibcode: 2016PhRvD..93d4027O. doi:10.1103/PhysRevD.93.044027. hdl:2164/5830. S2CID 119210226. Archived from the original on 2023-01-22. Retrieved 2021-01-01.
65.Oniga, Teodora; Wang, Charles H.-T. (2017-10-05). *“Quantum coherence, radiance, and resistance of gravitational systems”*. *Physical Review D*. 96 (8): 084014. [arXiv:1701.04122](https://arxiv.org/abs/1701.04122). Bibcode: 2017PhRvD..96h4014O. doi:10.1103/PhysRevD.96.084014. [hdl:2164/9320](https://hdl.handle.net/2164/9320). S2CID 54777871. Archived from the original on 2023-01-22. Retrieved 2021-01-01.

　　 66.Quiñones, D. A.; Oniga, T.; Varcoe, B. T. H.; Wang, C. H.-T. (2017-08-15). *“Quantum principle of sensing gravitational waves: From the zero-point fluctuations to the cosmological stochastic background of spacetime”*. *Physical Review D*. 96 (4): 044018. [arXiv:1702.03905](https://arxiv.org/abs/1702.03905). Bibcode: 2017PhRvD..96d4018Q. doi:10.1103/PhysRevD.96.044018. [hdl:2164/9150](https://hdl.handle.net/2164/9150). S2CID 55056264. Archived from the original on 2023-01-22. Retrieved 2021-01-02.
67.Oniga, Teodora; Wang, Charles H.-T. (2016-09-19). *“Spacetime foam induced collective bundling of intense fields”*. *Physical Review D*. 94 (6): 061501. [arXiv:1603.09193](https://arxiv.org/abs/1603.09193). Bibcode: 2016PhRvD..94f1501O. doi:10.1103/PhysRevD.94.061501. [hdl:2164/7434](https://hdl.handle.net/2164/7434). S2CID 54872718. Archived from the original on 2023-01-22. Retrieved 2021-01-02.
68.Vasileiou, Vlasios; Granot, Jonathan; Piran, Tsvi; Amelino-Camelia, Giovanni (2015-03-16). *“A Planck-scale limit on spacetime fuzziness and stochastic Lorentz invariance violation”*. *Nature Physics*. 11 (4): 344–346. Bibcode: 2015NatPh..11..344V. doi:10.1038/nphys3270. ISSN 1745-2473. S2CID 54727053.
69.The IceCube Collaboration; Abbasi, R.; Ackermann, M.; Adams, J.; et al. (2022-11-01). *“Search for quantum gravity using astrophysical neutrino flavour with IceCube”*. *Nature Physics*. 18 (11): 1287–1292. [arXiv:2111.04654](https://arxiv.org/abs/2111.04654). Bibcode: 2022NatPh..18.1287I. doi:10.1038/s41567-022-01762-1. ISSN 1745-2473. S2CID 243848123.
70.Abbasi, R. and others, IceCube Collaboration (June 2023). *“Searching for Decoherence from Quantum Gravity at the IceCube South Pole Neutrino Observatory”*. [arXiv:hep-ex/2308.00105](https://arxiv.org/abs/2308.00105).
71.“Integral challenges physics beyond Einstein”. European Space Agency. 2011-06-30. Archived from the original on 2021-11-13. Retrieved 2021-11-06.
72.Laurent, P.; Götz, D.; Binétruy, P.; Covino, S.; Fernandez-Soto, A. (2011-06-28). *“Constraints on Lorentz Invariance Violation using integral/IBIS observations of GRB041219A”*. *Physical Review D*. 83 (12): 121301. [arXiv:1106.1068](https://arxiv.org/abs/1106.1068). Bibcode: 2011PhRvD..83l1301L. doi:10.1103/PhysRevD.83.121301. ISSN 1550-7998. S2CID 53603505. Archived from the original on 2023-01-22. Retrieved 2021-11-06.
73.Cowen, Ron (2015-01-30). *“Gravitational waves discovery now officially dead”*. *Nature*. doi:10.1038/nature.2015.16830. S2CID 124938210.

8. 参考资料

9. 进一步阅读

10. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利