柯西-黎曼方程（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学的复分析领域，柯西–黎曼方程以奥古斯丁·柯西和伯恩哈德·黎曼命名，由一组二阶偏微分方程组成，这些方程为复变量的复函数可复微分的必要与充分条件。

　　 这些方程是： \[ \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \quad (1a)~ \]

　　 和 \[ \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x} \quad (1b)~ \] 其中，\(u(x, y)\) 和 \(v(x, y)\) 是实值的二元可微函数。

　　 通常，\(u\) 和 \(v\) 分别是复值函数 \(f(x+iy)=f(x,y)=u(x,y)+iv(x,y)\) 的实部和虚部，其中 \( z = x + iy \) 是单一复变量，且 \( x \) 和 \( y \) 是实变量；\( u \) 和 \( v \) 是实变量的实值可微函数。如果 \( f \) 在某个复数点可复微分，当且仅当 \( u \) 和 \( v \) 的偏导数在该点满足柯西–黎曼方程时，\( f \) 才是复微分的。

　　 全纯函数是指在复平面某个开子集的每一点都可微分的复函数。已经证明，全纯函数是解析的，而解析的复函数是复微分的。特别地，全纯函数是无限次可复微分的。

　　 微分性与解析性之间的等价性是所有复分析的起点。

1. 历史

　　 柯西–黎曼方程首次出现在让·勒·朗·达朗贝尔的研究中。\(^\text{[1]}\) 后来，莱昂哈德·欧拉将这一系统与解析函数联系起来。\(^\text{[2]}\) 随后，柯西使用这些方程构建了他的函数理论。\(^\text{[3]}\) 黎曼关于函数理论的博士论文于 1851 年发表。\(^\text{[4]}\)

2. 简单示例

　　 假设 \( z = x + iy \)。复值函数 \( f(z) = z^2 \) 在复平面上的任意点 \( z \) 都是可微分的。 \[ f(z) = (x + iy)^2 = x^2 - y^2 + 2ixy~ \] 实部 \( u(x, y) \) 和虚部 \( v(x, y) \) 分别为 \[ u(x, y) = x^2 - y^2, \quad v(x, y) = 2xy~ \] 它们的偏导数是 \[ u_x = 2x, \quad u_y = -2y, \quad v_x = 2y, \quad v_y = 2x~ \] 我们可以看到，柯西–黎曼方程确实成立，\(u_x = v_y\) 和 \(u_y = -v_x\).

3. 解释与重新表述

　　 柯西–黎曼方程是从复分析的角度看待函数可微分条件的一种方式：换句话说，它们通过常规的微分学方法来概括复变量函数的概念。在这一理论中，还有几种主要的方式来理解这一概念，通常需要将该条件转化为其他语言。

共形映射

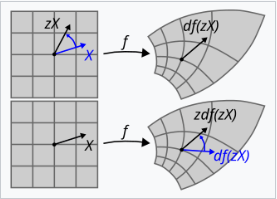
　　 首先，柯西–黎曼方程可以写成复数形式： \[ i \frac{\partial f}{\partial x} = \frac{\partial f}{\partial y}.~ \] 在这种形式下，方程在结构上对应于雅可比矩阵的形式： \[ \begin{pmatrix} a & -b \\ b & a \end{pmatrix},~ \] 其中 \(a=\partial u/\partial x=\partial v/\partial y\) 和 \(b=\partial v/\partial x=-\partial u/\partial y\).这种形式的矩阵是复数的矩阵表示。从几何上讲，这样的矩阵总是旋转与缩放的组合，特别是它保持角度不变。函数 \(f(z)\) 的雅可比矩阵将两个曲线交点处的无穷小线段旋转到 \(f(z)\) 中的相应线段。因此，满足柯西–黎曼方程且导数不为零的函数保持平面中曲线之间的角度。这就是说，柯西–黎曼方程是函数保持共形性的条件。

　　 此外，由于共形变换的组合仍然是共形的，柯西–黎曼方程的解与共形映射的组合必须自身满足柯西–黎曼方程。因此，柯西–黎曼方程是共形不变的。

复微分性

　　 设 \( f(z) = u(z) + i \cdot v(z) \)，其中 \( u \) 和 \( v \) 是实值函数，\( f \) 是复变量 \( z = x + iy \) 的复值函数，\(x\) 和 \(y\) 是实变量。 \[f(z) = f(x + iy) = f(x, y)~\] 因此，函数也可以看作是实变量 \(x\) 和 \(y\) 的函数。那么，复函数 \(f\) 在点 \( z_0 = x_0 + iy_0 \) 处的复导数定义为： \[ f'(z_0) = \lim_{\underset{h \in \mathbb{C}}{h \to 0}} \frac{f(z_0 + h) - f(z_0)}{h}~ \] 前提是该极限存在（即，沿着每一条趋近于 \( z_0 \) 的路径该极限存在，并且不依赖于选择的路径）。

　　 复分析的一个基本结果是，函数 \( f \) 在点 \( z_0 \) 处是复微分的（即，它具有复导数），当且仅当实值二元函数 \( u(x + iy) \) 和 \( v(x + iy) \) 在点 \( (x_0, y_0) \) 处可微分，并且在该点满足柯西–黎曼方程。\(^\text{[5][6][7]}\)

　　 事实上，如果复导数在 \( z_0 \) 处存在，那么可以通过沿实轴和虚轴在 \( z_0 \) 处取极限来计算复导数，并且这两个极限必须相等。沿实轴时，极限为： \[ \lim_{\underset{h \in \mathbb{R}}{h \to 0}} \frac{f(z_0 + h) - f(z_0)}{h} = \left. \frac{\partial f}{\partial x} \right|_{z_0}~ \] 而沿虚轴时，极限为： \[ \lim_{\underset{h \in \mathbb{R}}{h \to 0}} \frac{f(z_0 + ih) - f(z_0)}{ih} = \left. \frac{1}{i} \frac{\partial f}{\partial y} \right|_{z_0}~ \] 因此，导数的相等性意味着： \[ i \left. \frac{\partial f}{\partial x} \right|_{z_0} = \left. \frac{\partial f}{\partial y} \right|_{z_0}~ \] 这就是柯西–黎曼方程在 \( z_0 \) 处的复数形式。

　　 （注意，如果 \( f \) 在 \( z_0 \) 处是复微分的，那么它也是实微分的，并且 \( f \) 在 \( z_0 \) 处的雅可比矩阵是复数标量 \( f'(z_0) \)，可以看作是 \( \mathbb{C} \) 上的实线性映射，因为极限 \(|f(z) - f(z_0) - f'(z_0)(z - z_0)|/|z - z_0| \to 0\) 和 \(z \to z_0\) 成立。）

　　 相反，如果 \( f \) 在 \( z_0 \) 处（在实数意义下）是可微分的，并且在该点满足柯西-黎曼方程，那么它在该点是复微分的。假设 \( f \) 作为两个实变量 \( x \) 和 \( y \) 的函数在 \( z_0 \) 处是可微分的（即实微分的）。这等价于存在以下线性近似： \[ \Delta f(z_0) = f(z_0 + \Delta z) - f(z_0) = f_x \Delta x + f_y \Delta y + \eta(\Delta z)~ \] 其中 \(f_x = \left. \frac{\partial f}{\partial x} \right|_{z_0}, \quad f_y = \left. \frac{\partial f}{\partial y} \right|_{z_0}, \quad z = x + iy, \quad \eta(\Delta z) / |\Delta z| \to 0\) 当 \(\Delta z \to 0\).

　　 由于 \(\Delta z + \Delta \bar{z} = 2 \Delta x \) 和 \(\Delta z - \Delta \bar{z} = 2i \Delta y\),上述表达式可以重新写为： \[ \Delta f(z_0) = \frac{f_x - i f_y}{2} \Delta z + \frac{f_x + i f_y}{2} \Delta \bar{z} + \eta(\Delta z)~ \] \[ \frac{\Delta f}{\Delta z} = \frac{f_x - i f_y}{2} + \frac{f_x + i f_y}{2} \cdot \frac{\Delta \bar{z}}{\Delta z} + \frac{\eta(\Delta z)}{\Delta z}, \quad (\Delta z \neq 0).~ \] 现在，如果 \( \Delta z \) 是实数，则有 \(\Delta \bar{z}/\Delta z=1\)，而如果它是虚数，则有 \(\Delta \bar{z}/\Delta z=-1\)。因此，第二项在 \( \Delta z \to 0 \) 的极限路径上是独立的，只有当它恒等地消失时才成立：\(f_x + i f_y = 0\),这正是柯西–黎曼方程的复数形式。这个证明还表明，在这种情况下， \[ \left. \frac{df}{dz} \right|_{z_0} = \lim_{\Delta z \to 0} \frac{\Delta f}{\Delta z} = \frac{f_x - i f_y}{2}.~ \] 请注意，点 \( z_0 \) 处实微分性假设是必要的，不能省略。例如，\(^\text{[8]}\) 函数 \(f(x, y)=\sqrt{|xy|}\)，作为一个复函数，其虚部恒为零，在点 \((x_0, y_0) = (0, 0)\) 处具有偏导数，并且在该点满足柯西–黎曼方程，但它不是在实函数（多变量函数）意义下可微的，因此，第一个条件——实微分性——没有满足。因此，这个函数不是复微分的。

　　 一些来源 \(^\text{[9][10]}\) 指出，复微分性在点 \(z_0\) 处的充分条件是，除了满足柯西–黎曼方程外，\( u \) 和 \( v \) 的偏导数在该点处是连续的，因为这一连续性条件确保了上述线性近似的存在。请注意，这不是复微分性的必要条件。例如，函数 \(f(z) = z^2 e^{i/|z|}\) 在 \( z = 0 \) 处是复微分的，但其实部和虚部在该点的偏导数是间断的。由于复微分性通常是在开集内考虑的，而在开集内复微分性实际上意味着所有偏导数是连续的（见下文），因此这一区分在文献中通常被省略。

复共轭的独立性

　　 上述证明提示了柯西–黎曼方程的另一种解释。复共轭 \( z \)（记作 \( \bar{z} \)）定义为 \[ x + iy \quad \text{的复共轭} := x - iy~ \] 其中 \( x \) 和 \( y \) 是实变量。定义两个维尔廷格导数为 \[ \frac{\partial}{\partial z} = \frac{1}{2} \left( \frac{\partial}{\partial x} - i \frac{\partial}{\partial y} \right), \quad \frac{\partial}{\partial \bar{z}} = \frac{1}{2} \left( \frac{\partial}{\partial x} + i \frac{\partial}{\partial y} \right),~ \] 那么柯西–黎曼方程可以写成一个单一的方程： \[ \frac{\partial f}{\partial \bar{z}} = 0,~ \] 在这种情况下，\( f \) 的复导数为 \[ \frac{df}{dz} = \frac{\partial f}{\partial z}.~ \] 在这种形式下，柯西–黎曼方程可以解释为复函数 \( f \) 对复变量 \( z \) 的依赖性，而与变量 \( \bar{z} \) 无关。因此，我们可以将解析函数视为一个复变量 \( z \) 的真正函数，而不是两个实变量 \( x \) 和 \( y \) 的复函数。

物理解释

　　 柯西–黎曼方程的一个标准物理解释，追溯到黎曼在函数理论中的工作 \(^\text{[11]}\)，是 \( u \) 代表平面中不可压缩稳态流体流动的速度势，而 \( v \) 是其流函数。假设这对（两次连续可微的）函数 \( u \) 和 \( v \) 满足柯西–黎曼方程。我们将 \( u \) 视为速度势，这意味着我们假设平面中有一个流体流动，在平面上每一点的流体速度矢量等于 \( u \) 的梯度，定义为 \[ \nabla u = \frac{\partial u}{\partial x} \mathbf{i} + \frac{\partial u}{\partial y} \mathbf{j}.~ \] 通过对柯西–黎曼方程对 \( u \) 和 \( v \) 进行求导，并利用二阶导数的对称性，可以证明 \( u \) 满足拉普拉斯方程： \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0.~ \] 也就是说，\( u \) 是一个调和函数。这意味着梯度的散度为零，因此流体是不可压缩的。

　　 通过类似的分析，函数 \( v \) 也满足拉普拉斯方程。此外，柯西–黎曼方程意味着点积 \(\nabla u \cdot \nabla v = 0\) 即 \[ (\nabla u \cdot \nabla v = \frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \cdot \frac{\partial v}{\partial y} = \frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} - \frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} = 0),~ \] 也就是说，\( u \) 和 \( v \) 的最大坡度方向是相互垂直的。这意味着 \( u \) 的梯度必须沿着 \( v = \text{const} \) 曲线指向；因此，这些曲线是流线。\( u = \text{const} \) 曲线是流动的等势线。

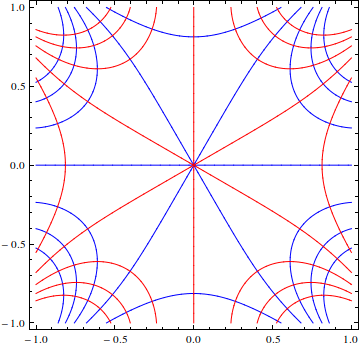
　　 因此，全纯函数可以通过绘制 \( u = \text{const} \) 和 \( v = \text{const} \) 的两组等高线来可视化。在 \( u \)（或等效地 \( v \)）的梯度不为零的点附近，这两组曲线形成一组正交的曲线族。在 \( \nabla u = 0 \) 的点，流动的驻点，\( u = \text{const} \) 的等势线交汇。流线也在同一点交汇，并平分由等势线形成的角度。

调和向量场

　　 柯西–黎曼方程的另一个解释可以在 Pólya 和 Szegő 的著作中找到。\(^\text{[12]}\) 假设 \( u \) 和 \( v \) 在 \(\mathbb{R}^2 \) 的一个开子集上满足柯西–黎曼方程，并考虑向量场 \[ \bar{f} = \begin{bmatrix} u \\ -v \end{bmatrix}~ \] 将其视为一个（实数）二维向量。然后，第二个柯西–黎曼方程（1b）表明 \( \bar{f} \) 是无旋的（其旋度为零）： \[ \frac{\partial (-v)}{\partial x} - \frac{\partial u}{\partial y} = 0.~ \] 第一个柯西–黎曼方程（1a）表明该向量场是无散的（或散度为零）： \[ \frac{\partial u}{\partial x} + \frac{\partial (-v)}{\partial y} = 0.~ \] 根据格林定理和散度定理，这样的场必定是保守场，并且没有源或汇，其通过任何没有孔的开放区域的净通量为零。（这两个观察结果在柯西积分定理中结合为实部和虚部。）在流体动力学中，这样的向量场是势流。\(^\text{[13]}\) 在静磁学中，这样的向量场模拟的是平面区域中没有电流的静态磁场。在静电学中，它们模拟的是平面区域中没有电荷的静态电场。

　　 这个解释可以等价地用微分形式的语言重新表述。如果且仅如果一对 \( u \) 和 \( v \) 满足柯西–黎曼方程，那么一形式 \(v\,dx + u\,dy\) 既是闭合的又是余闭合的（即调和微分形式）。

复结构的保持

　　 柯西–黎曼方程的另一种表述涉及平面中的复结构，给定为 \[ J = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}.~ \] 这是一个复结构，因为 \( J \) 的平方是 \(2\times2\) 单位矩阵的负数：\(J^2 = -I\).如上所述，如果 \( u(x, y) \) 和 \( v(x, y) \) 是平面中的两个函数，定义 \[ f(x, y) = \begin{bmatrix} u(x, y) \\ v(x, y) \end{bmatrix}.~ \] 则 \( f \) 的雅可比矩阵是偏导数矩阵 \[ D f(x, y) = \begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{bmatrix}.~ \] 如果且仅如果 \(2\times2\) 矩阵 \( Df \) 与 \( J \) 对易，则一对函数 \( u, v \) 满足柯西–黎曼方程。\(^\text{[14]}\)

　　 这种解释在辛几何中非常有用，它是研究伪全纯曲线的起点。

其他形式表示法

　　 在其他坐标系中，柯西–黎曼方程有时会有不同的表示形式。如果一对可微函数 \( u \) 和 \( v \) 满足（1a）和（1b），那么它们也满足： \[ \frac{\partial u}{\partial n} = \frac{\partial v}{\partial s}, \quad \frac{\partial v}{\partial n} = -\frac{\partial u}{\partial s}~ \] 对于任意一组坐标系 \( (n(x, y), s(x, y)) \)，只要向量对 \( (\nabla n, \nabla s) \) 是正交且具有正定方向（即正向正交）。因此，特别是在以极坐标表示 \( z = re^{i\theta} \) 的坐标系中，方程变为： \[ \frac{\partial u}{\partial r} = \frac{1}{r} \frac{\partial v}{\partial \theta}, \quad \frac{\partial v}{\partial r} = -\frac{1}{r} \frac{\partial u}{\partial \theta}.~ \] 将它们合并为对函数 \( f \) 的一个等式，得： \[ \frac{\partial f}{\partial r} = \frac{1}{ir} \frac{\partial f}{\partial \theta}.~ \] 非齐次形式的柯西–黎曼方程由一对未知函数 \( u(x, y) \) 和 \( v(x, y) \) 的两个实变量方程组成： \[ \begin{aligned} \frac{\partial u}{\partial x} - \frac{\partial v}{\partial y} &= \alpha(x, y) \\ \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} &= \beta(x, y) \end{aligned}~ \] 其中 \( \alpha(x, y) \) 和 \( \beta(x, y) \) 是定义在 \( \mathbb{R}^2 \) 某个开子集上的已知函数。 这些方程通常可以合并为一个单一的复形式方程： \[ \frac{\partial f}{\partial \bar{z}} = \varphi(z, \bar{z})~ \] 其中 \( f = u + iv \)，且 \( \varphi = \alpha + i\beta/2\)。

　　 如果 \( \varphi \) 是 \( C^k \) 类函数（即 \( k \) 次连续可微），并且 \( \varphi \) 在有界区域 \( D \) 的闭包上是连续的，那么该非齐次方程在 \( D \) 内显式可解。确实，根据柯西积分公式，有： \[ f(\zeta, \bar{\zeta}) = \frac{1}{2\pi i} \iint_D \varphi(z, \bar{z}) \cdot \frac{dz \wedge d\bar{z}}{z - \zeta},~ \] 对于所有 \(\zeta \in D\)。

4. 广义化

高尔萨特定理及其广义

　　 假设 \( f = u + iv \) 是一个复值函数，且作为函数 \( f: \mathbb{R}^2 \to \mathbb{R}^2 \) 可微。则高尔萨特定理断言，当且仅当 \( f \) 在开复数域 \( \Omega \) 中满足柯西–黎曼方程时，\( f \) 在该域内是解析的。\(^\text{[15]}\) 特别地，不需要假设 \( f \) 是连续可微的。\(^\text{[16]}\)

　　 高尔萨特定理的假设可以显著放宽。如果 \( f = u + iv \) 在开集 \( \Omega \) 中连续，并且 \( f \) 关于 \( x \) 和 \( y \) 的偏导数在 \( \Omega \) 中存在，且在 \( \Omega \) 中满足柯西–黎曼方程，则 \( f \) 是全纯的（因此是解析的）。这一结果即为洛曼–门乔夫定理。

　　 假设 \( f \) 在域 \( \Omega \) 中满足柯西–黎曼方程是必不可少的。确实，可以构造一个在某一点满足柯西–黎曼方程，但在该点不是解析的连续函数（例如，\( f(z)=z^5/|z|^4\)）。类似地，除了柯西–黎曼方程之外，还需要一些额外的假设（如连续性），正如下例所示 \(^\text{[17]}\)： \[ f(z) = \begin{cases} \exp\left(-z^{-4}\right) & \text{如果 } z \neq 0 \\ 0 & \text{如果 } z = 0 \end{cases}~ \] 该函数在所有点上满足柯西–黎曼方程，但在 \( z = 0 \) 处不连续。

　　 然而，如果一个函数在开集内以弱意义满足柯西–黎曼方程，那么该函数是解析的。更准确地说：\(^\text{[18]}\)

　　 如果 \( f(z) \) 在开域 \( \Omega \subset \mathbb{C} \) 中是局部可积的，并且在弱意义上满足柯西–黎曼方程，则 \( f \) 在 \( \Omega \) 中几乎处处与一个解析函数一致。

　　 这实际上是关于拟椭圆型偏微分方程解的正则性的更一般结果的特例。

多个变量

　　 在多个复变量的理论中，存在适当推广的柯西-黎曼方程。它们构成了一个重要的超定常微分方程系统。这是通过对 Wirtinger 导数的简单推广实现的，在这种推广中，所讨论的函数要求对于每个复变量的（偏）Wirtinger 导数都为零。

复数微分形式

　　 通常的表述是，d-bar 算符 \({\displaystyle {\bar {\partial }}}\) 将全纯函数湮灭。这最直接地推广了如下的表述： \[ {\displaystyle {\partial f \over \partial {\bar {z}}}=0,}~ \] 其中： \[ {\displaystyle {\partial f \over \partial {\bar {z}}}={1 \over 2}\left({\partial f \over \partial x}+i{\partial f \over \partial y}\right).}~ \]

Bäcklund 变换

　　 将柯西–黎曼方程视为共轭调和函数，它们是 Bäcklund 变换的一个简单例子。更复杂的、通常是非线性的 Bäcklund 变换，如正弦–戈登方程中的变换，在孤立子理论和可积系统中具有重要意义。

克利福德代数中的定义

　　 在克利福德代数 \({\displaystyle C\ell (2)}\) 中，复数 \({\displaystyle z=x+iy}\) 被表示为 \({\displaystyle z\equiv x+Jy}\)，其中(\({\displaystyle J\equiv \sigma_1\sigma_2}\)，且 \({\displaystyle \sigma_1^2=\sigma_2^2=1,\ \sigma_1\sigma_2+\sigma_2\sigma_1=0}\)，因此 \({\displaystyle J^2=-1}\))。该克利福德代数中的 Dirac 算符定义为 \({\displaystyle \nabla \equiv \sigma_1\partial_x + \sigma_2\partial_y}\)。当且仅当函数 \({\displaystyle f=u+Jv}\) 满足 \({\displaystyle \nabla f=0}\) 时，该函数被视为解析函数，具体计算如下： \[ 0 = \nabla f = (\sigma_1 \partial_x + \sigma_2 \partial_y)(u + \sigma_1\sigma_2 v)~ \] 展开后得到： \[ = \sigma_1 \partial_x u + \underbrace{\sigma_1 \sigma_1 \sigma_2}_{=\sigma_2} \partial_x v + \sigma_2 \partial_y u + \underbrace{\sigma_2 \sigma_1 \sigma_2}_{=-\sigma_1} \partial_y v = 0~ \] 按 \({\displaystyle \sigma_1}\) 和 \({\displaystyle \sigma_2}\) 分组： \[ \nabla f = \sigma_1 (\partial_x u - \partial_y v) + \sigma_2 (\partial_x v + \partial_y u) = 0~ \] 因此得到： \[ \Rightarrow \begin{cases} \partial_x u - \partial_y v = 0 \\ \partial_x v + \partial_y u = 0 \end{cases}~ \] 因此，用传统符号表示为： \[ \begin{cases} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \\\\ \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} \end{cases}~ \]

高维中的保形映射

　　 设 \(\Omega\) 是欧几里得空间 \({\displaystyle \mathbb {R} ^{n}}\) 中的一个开集。保持方向的映射 \({\displaystyle f:\Omega \to \mathbb {R} ^{n}}\) 是保形映射（即保持角度的映射）的方程为： \[ D f^{\mathsf{T}} D f = (\det(Df))^{2/n} I~ \] 其中，\({\displaystyle Df}\) 是雅可比矩阵，\({\displaystyle Df^{\mathsf{T}}}\) 是其转置，\({\displaystyle I}\) 表示单位矩阵。[19] 当 \(n = 2\) 时，该系统等价于复变函数的标准柯西–黎曼方程，解是全纯函数。在 \(n > 2\) 的维度中，这仍然有时被称为柯西–黎曼系统，并且李维尔定理在适当的光滑性假设下暗示，任何这样的映射都是莫比乌斯变换。

李群伪群

　　 参见：伪群 我们可以通过更一般地提出，求解系统的解在复合下何时是封闭的来推广柯西–黎曼方程。李伪群理论解决了这类问题。

5. 参见

• 复杂分析主题列表
• 柯西积分定理
• 莫雷拉定理
• Wirtinger 导数

6. 参考文献

1. 达朗贝尔，让（1752 年）。《流体阻力新理论初探》。巴黎：大卫老店。2018 年由 Hachette Livre-BNF 再版，ISBN 978-2012542839。
2. 欧拉，莱昂哈德（1797 年）。《关于虚数积分公式的进一步研究》。《圣彼得堡皇家科学院新学报》，第 10 卷，第 3–19 页。
3. 柯西，奥古斯丁·L.（1814 年）。《论定积分》。载于《柯西全集·第一辑·第一卷》（1882 年出版）。巴黎，第 319–506 页。
4. 黎曼，伯恩哈德（1851 年）。《关于可变复数量函数的一般理论基础》。H.韦伯（编），《黎曼数学全集》（德文版）。多佛出版社（1953 年出版），第 3–48 页。
5. 鲁丁 1966。
6. 马斯登与霍夫曼 1973。
7. 马尔库舍维奇，A.I.（1977 年）。《复变函数论 第 1 卷》。切尔西出版社，第 110–112 页（译自俄语）。
8. 蒂奇马什，E.（1939 年）。《函数论》。牛津大学出版社，2.14 节。
9. 阿夫肯，乔治·B.；韦伯，汉斯·J.；哈里斯，弗兰克·E.（2013 年）。《11.2 柯西-黎曼条件》。载于《物理学家数学方法：综合指南（第七版）》。学术出版社，第 471–472 页。ISBN 978-0-12-384654-9。
10. 哈桑尼，萨德里（2013 年）。《10.2 解析函数》。载于《数学物理：现代基础导论（第二版）》。斯普林格出版社，第 300–301 页。ISBN 978-3-319-01195-0。
11. 克莱因，菲利克斯（1893 年）。《论黎曼的代数函数及其积分理论》。弗朗西丝·哈德卡斯尔（译）。剑桥：麦克米伦与鲍斯出版社。
12. 波利亚，乔治；塞格，加博尔（1978 年）。《分析中的问题与定理 第一卷》。斯普林格出版社。ISBN 3-540-63640-4。
13. 尚松，H.（2007 年）。《Le Potentiel de Vitesse pour les Ecoulements de Fluides Réels: la Contribution de Joseph-Louis Lagrange》[真实流体流动中的速度势：约瑟夫-路易·拉格朗日的贡献]。《Journal la Houille Blanche》，第 93 卷，第 5 期，第 127–131 页。doi:10.1051/lhb:2007072。ISSN 0018-6368。S2CID 110258050。
14. 小林昭七；野水克己（1969 年）。《微分几何基础 第二卷》。威利出版社。命题 IX.2.2。
15. 鲁丁 1966，定理 11.2。
16. 迪厄多内，让·亚历山大（1969 年）。《现代分析基础》。学术出版社。第 9.10 节，习题 1。
17. 鲁曼 1923，第 107 页。
18. 格雷与莫里斯 1978，定理 9。
19. 伊万涅茨，T.；马丁，G.（2001 年）。《几何函数论与非線性分析》。牛津出版社。第 32 页。

7. 参考文献

• 格雷，J. D.；莫里斯，S. A.（1978 年 4 月）。《满足柯西-黎曼方程的函数何时解析？》。《美国数学月刊》，第 85 卷，第 4 期，第 246–256 页。doi:10.2307/2321164。JSTOR 2321164。
• 鲁曼，H.（1923 年）。《Über die Cauchy–Riemannschen Differentialgleichungen》[论柯西-黎曼微分方程]。《哥廷根学报》（德文），第 97–108 页。
• 马斯登，A.；霍夫曼，M.（1973 年）。《基础复分析》。W. H. 弗里曼出版社。
• 鲁丁，沃尔特（1966 年）。《实分析与复分析（第三版）》。麦格劳-希尔出版社（1987 年出版）。ISBN 0-07-054234-1。

8. 延伸阅读

• 阿尔福斯，拉斯（1953 年）。《复分析（第三版）》。麦格劳-希尔出版社（1979 年出版）。ISBN 0-07-000657-1。
• 索洛门采夫，E.D.（2001 年）[1994 年]。《柯西-黎曼条件》。载于《数学百科全书》。EMS 出版社。
• 斯图尔特，伊恩；托尔，大卫（1983 年）。《复分析（第一版）》。剑桥大学出版社（1984 年出版）。ISBN 0-521-28763-4。

9. 外部链接

• 韦斯坦，埃里克·W.《柯西-黎曼方程》。MathWorld。
• 《柯西-黎曼方程模块（作者：John H. Mathews）》