级数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在数学中，级数大致而言就是将无限多个项一个接一个地相加。[1]对级数的研究是微积分及其推广——数学分析——的重要组成部分。级数在数学的大多数领域都有应用，甚至在组合学中研究有限结构时，也会通过生成函数来使用级数。无限级数的数学性质使其在物理学、计算机科学、统计学和金融等其他定量学科中也得到了广泛应用。

　　 在古希腊人看来，一个 “潜在无限” 的求和可以得到一个有限的结果，这被认为是悖论，其中最著名的例子就是芝诺悖论。[2][3]尽管如此，古希腊数学家们，包括阿基米德，仍然在实践中使用了无限级数，例如在抛物线求积问题中。[4][5]芝诺悖论中的数学问题在 17 世纪通过 “极限” 概念得到了化解，尤其是通过艾萨克·牛顿的早期微积分。[6]在 19 世纪，通过卡尔·弗里德里希·高斯和奥古斯丁-路易·柯西等人的工作，这一解决方案得到了进一步的严格化与改进。[7]他们回答了哪些和式是存在的问题（通过实数的完备性），以及级数项是否可以重新排列而不改变其和的问题（通过绝对收敛与条件收敛的概念）。

　　 在现代术语中，任何一个有序的无限序列 $(a_{1}, a_{2}, a_{3}, \ldots)$，无论这些项是数字、函数、矩阵，还是其他可以相加的对象，都定义了一个级数，即把这些 $a_i$ 一个接一个地相加。为了强调项的数量是无限的，级数常常也被称为无限级数，以区别于有限级数，后者有时用来指有限和。级数通常写作： $$ a_{1} + a_{2} + a_{3} + \cdots ,~ $$ 或者使用大写希腊字母 Σ 的求和符号表示：[8] $$ \sum_{i=1}^{\infty} a_i .~ $$ 由于级数所表达的无限次加法无法在有限时间内逐一完成，但如果这些项及其有限部分和属于一个具有极限的集合，就可能为该级数赋予一个值，称为级数的和。这个值定义为：当 $n \to \infty$ 时，级数前 $n$ 项的部分和的极限（若该极限存在）。[9][10][11] 这些有限和称为部分和。用求和符号表示： $$ \sum_{i=1}^{\infty} a_i = \lim_{n \to \infty} \sum_{i=1}^{n} a_i ,~ $$ 若极限存在。[9][10][11]当极限存在时，该级数称为收敛或可和，此时序列 $(a_{1}, a_{2}, a_{3}, \ldots)$ 也是可和的；反之，如果极限不存在，则称该级数发散。[9][10][11] 表达式 $\sum_{i=1}^{\infty} a_{i}$ 既表示级数——即无限地一个接一个相加项的隐含过程——又在该级数收敛时表示级数的和——即这一过程的明确极限。这是对类似约定的一种推广：例如 $a+b$ 既表示 “加法” 这一过程，也表示其结果——$a$ 与 $b$ 的和。

　　 通常，级数的项来自某个环，最常见的是实数域 $\mathbb{R}$ 或复数域 $\mathbb{C}$。在这种情况下，所有级数的集合本身也构成一个环，其中的加法是逐项相加，而乘法则由柯西乘积定义。[12][13][14]

1. 定义

级数

　　 一个级数，或更完整地说，无限级数，就是一个无限和。它通常表示为：[8][15][16] $$ a_{0} + a_{1} + a_{2} + \cdots \quad \text{或} \quad a_{1} + a_{2} + a_{3} + \cdots ,~ $$ 其中各项 $a_{k}$ 是一个数列（序列）的成员，这些成员可以是数、函数，或任何可以相加的对象。级数也常用大写希腊字母 Σ 的符号来表示：[8][16] $$ \sum_{k=0}^{\infty} a_{k} \quad \text{或} \quad \sum_{k=1}^{\infty} a_{k}.~ $$ 另外，一种常见的表示方法是写出前若干项，加上省略号，再写出一般项，最后再加省略号，其中一般项是 $n$ 的函数形式的第 $n$ 项： $$ a_{0} + a_{1} + a_{2} + \cdots + a_{n} + \cdots \quad \text{或} \quad f(0) + f(1) + f(2) + \cdots + f(n) + \cdots .~ $$ 例如，欧拉常数 $e$ 可以通过以下级数定义： $$ \sum_{n=0}^{\infty} \frac{1}{n!} = 1 + 1 + \frac{1}{2} + \frac{1}{6} + \cdots + \frac{1}{n!} + \cdots ,~ $$ 其中 $n!$ 表示前 $n$ 个正整数的乘积，而按照约定 $0! = 1$。[17][18][19]

级数的部分和

　　 给定一个级数 $s = \sum_{k=0}^{\infty} a_k $,它的第 $n$ 个**部分和**定义为：[9][10][11][16] $$ s_{n} = \sum_{k=0}^{n} a_k = a_0 + a_1 + \cdots + a_n .~ $$ 有些作者会直接把一个级数与其部分和序列等同。[9][11] 无论是部分和序列还是项的序列，都能完全刻画这个级数。而且，项的序列可以通过部分和序列的相邻差来恢复： $$ a_{n} = s_{n} - s_{n-1}.~ $$ 数列的部分求和是线性序列变换的一个例子，在计算机科学中也称为前缀和。而从部分和恢复原数列的逆变换就是有限差分，这也是另一种线性序列变换。

　　 有时，级数的部分和具有更简单的闭合形式。例如：等差级数的部分和： $$ s_{n} = \sum_{k=0}^{n} (a + kd) = a + (a+d) + (a+2d) + \cdots + (a+nd) = (n+1)\left(a + \tfrac{1}{2}nd\right) .~ $$ 等比级数的部分和：[20][21][22] $$ s_{n} = \sum_{k=0}^{n} ar^{k} = a + ar + ar^{2} + \cdots + ar^{n} = a \cdot \frac{1-r^{\,n+1}}{1-r}, \quad \text{当 } r \neq 1,~ $$ 或者更简单地写成： $$ s_{n} = a(n+1), \quad \text{当 } r = 1.~ $$

级数的和

图
图 1：三种几何级数及其从第 1 项到第 6 项部分和的示意图。虚线表示极限。

　　 严格来说，当一个级数的部分和序列存在极限时，就称这个级数收敛、是收敛的，或是可和的。当部分和序列的极限不存在时，就称该级数发散或是发散的。[23]当部分和的极限存在时，它被称为级数的和或级数的值：[9][10][11][16] $$ \sum_{k=0}^{\infty} a_{k} = \lim_{n \to \infty} \sum_{k=0}^{n} a_{k} = \lim_{n \to \infty} s_{n}.~ $$ 只有有限个非零项的级数总是收敛的。这样的级数在处理有限和时很有用，无需关心项数的多少。[24]

　　 当和存在时，级数的和与它的第 $n$ 个部分和之间的差：$s - s_{n} = \sum_{k=n+1}^{\infty} a_{k}$,称为该无限级数的第 $n$ 阶截断误差。[25][26]

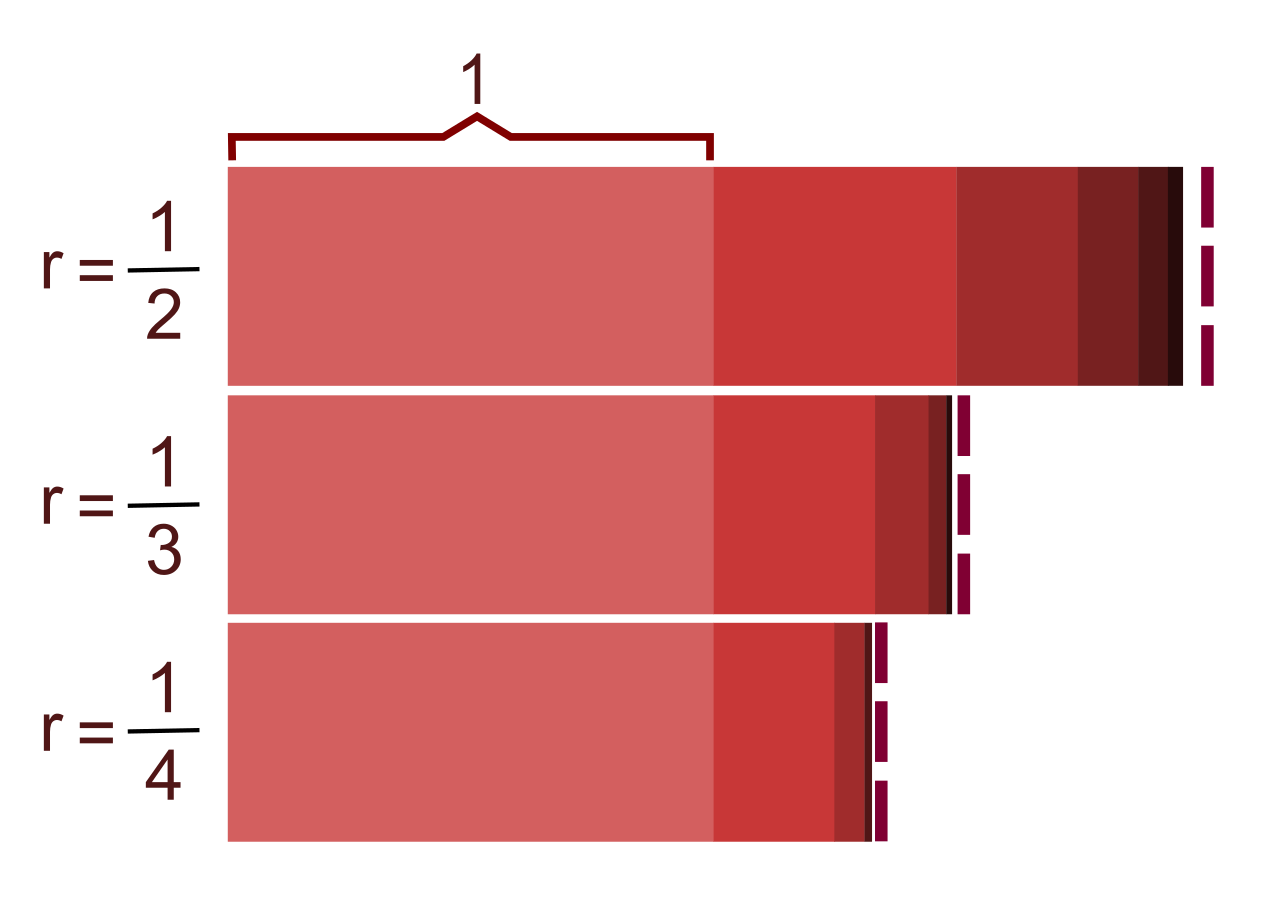
　　 一个收敛级数的例子是几何级数： $$ 1 + \tfrac{1}{2} + \tfrac{1}{4} + \tfrac{1}{8} + \cdots + \tfrac{1}{2^{k}} + \cdots .~ $$ 通过代数运算可以证明，它的第 $n$ 个部分和 $s_{n}$ 为： $$ \sum_{k=0}^{n} \tfrac{1}{2^{k}} = 2 - \tfrac{1}{2^{n}} .~ $$ 由于 $$ \lim_{n \to \infty} \left( 2 - \tfrac{1}{2^{n}} \right) = 2 ,~ $$ 该级数收敛，并且其和为 $2$，其第 $n$ 阶截断误差为 $\tfrac{1}{2^{n}}$。[20][21][22]

　　 相比之下，几何级数 $$ \sum_{k=0}^{\infty} 2^{k}~ $$ 在实数范围内是发散的。[20][21][22] 然而，在扩展实数轴上，它是收敛的，其极限为 $+\infty$，并且在每一步的截断误差也为 $+\infty$。[27]

　　 当一个级数的部分和序列不易直接计算和检验其收敛性时，可以使用收敛性判别法来证明该级数是收敛还是发散。

2. 分组与重排项

分组

　　 在普通的有限求和中，由于加法的结合律，和式中的项可以任意分组或拆分，而不会改变求和的结果： $$ a_{0} + a_{1} + a_{2} = a_{0} + (a_{1} + a_{2}) = (a_{0} + a_{1}) + a_{2}.~ $$ 类似地，在一个级数中，任何有限次分组都不会改变其部分和的极限，因此不会改变级数的和。但是，如果在一个无限级数中进行无限次分组，那么分组后的部分和可能会有不同于原级数的极限，而不同的分组方式之间也可能得到不同的极限。例如：原和式 $a_{0} + a_{1} + a_{2} + \cdots$ 的和不一定等于分组形式 $a_{0} + (a_{1}+a_{2}) + (a_{3}+a_{4}) + \cdots $.

　　 例如，格兰迪级数 $1 - 1 + 1 - 1 + \cdots$ 的部分和序列在 1 与 0 之间来回交替，因此它不收敛。若将项成对分组，可得：$(1-1) + (1-1) + (1-1) + \cdots = 0 + 0 + 0 + \cdots $,其部分和恒为 0，因此和为 0。如果从第一项后开始成对分组，则得到：$1 + (-1+1) + (-1+1) + \cdots = 1 + 0 + 0 + \cdots $,其部分和恒为 1，因此和为 1，与前一种分组方式结果不同。

　　 一般来说，将级数分组会得到一个新的级数，其部分和序列是原级数部分和序列的子序列。这意味着：如果原级数收敛，则分组后的新级数也收敛，并且极限相同——因为收敛数列的任意无限子序列也收敛到同一极限。但是，如果原级数发散，则分组后的级数不一定发散，就像上述格兰迪级数的例子。然而，如果分组后的级数发散，则必然说明原级数发散，因为这表明原级数部分和序列存在一个不收敛的子序列，而这在收敛的情况下是不可能的。

　　 这一推理曾被奥雷姆用来证明调和级数发散[28]，并且是一般柯西凝聚判别法的基础。[29][30]

重排

　　 在普通的有限求和中，由于加法的交换律，和式中的项可以任意重排，而不会改变求和的结果：$a_{0} + a_{1} + a_{2} = a_{0} + a_{2} + a_{1} = a_{2} + a_{1} + a_{0}$.类似地，在一个级数中，任何有限次重排都不会改变其部分和的极限，因此不会改变级数的和：对于任何有限的重排，总存在某一项之后，重排对后续项不再产生影响；这样，重排的影响仅限于有限项的求和，而有限和在重排下是不变的。

　　 然而，就像分组一样，在一个无限级数中进行无限次重排，有时可能会改变部分和的极限。那些部分和序列收敛于某个值，但其项可以被重新排列成另一个级数，而该级数的部分和却收敛于不同值的情形，被称为条件收敛级数。而无论如何重排都收敛于同一个值的，则称为无条件收敛级数。

　　 对于实数或复数项的级数：$a_{0} + a_{1} + a_{2} + \cdots$ 当且仅当其项的绝对值级数 $|a_{0}| + |a_{1}| + |a_{2}| + \cdots$ 也收敛时，它是无条件收敛的。这一性质称为绝对收敛。否则，若一个实数或复数级数收敛但并非绝对收敛，它就是条件收敛的。

　　 任何实数条件收敛级数都可以通过重新排列其项，使其和收敛到任意一个给定的实数，甚至可以使其发散。这一结论就是黎曼级数定理的内容。[31][32][33]

　　 一个历史上重要的条件收敛的例子是交错调和级数： $$ \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots ,~ $$ 它的和等于自然对数 $\ln 2$。而其项的绝对值之和则是**调和级数**： $$ \sum_{n=1}^{\infty} \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots ,~ $$ 由于调和级数发散，[28] 所以交错调和级数是条件收敛的。例如，将交错调和级数的项重新排列，使得原级数中的每一个正项后面跟着两个负项（而不是一个），则得到：[34] $$ 1 - \tfrac{1}{2} - \tfrac{1}{4} + \tfrac{1}{3} - \tfrac{1}{6} - \tfrac{1}{8} + \tfrac{1}{5} - \tfrac{1}{10} - \tfrac{1}{12} + \cdots~ $$ $$ = \left(1 - \tfrac{1}{2}\right) - \tfrac{1}{4} + \left(\tfrac{1}{3} - \tfrac{1}{6}\right) - \tfrac{1}{8} + \left(\tfrac{1}{5} - \tfrac{1}{10}\right) - \tfrac{1}{12} + \cdots~ $$ $$ = \tfrac{1}{2} - \tfrac{1}{4} + \tfrac{1}{6} - \tfrac{1}{8} + \tfrac{1}{10} - \tfrac{1}{12} + \cdots~ $$ $$ = \tfrac{1}{2}\left(1 - \tfrac{1}{2} + \tfrac{1}{3} - \tfrac{1}{4} + \tfrac{1}{5} - \tfrac{1}{6} + \cdots\right),~ $$ 这正好是原交错调和级数的 $\tfrac{1}{2}$，因此它的和是 $\tfrac{1}{2}\ln 2$。根据黎曼级数定理，通过重新排列交错调和级数的项，可以使其和变为任意一个实数，甚至使其发散。

3. 运算

级数的加法

　　 两个级数 $a_{0} + a_{1} + a_{2} + \cdots \quad \text{和} \quad b_{0} + b_{1} + b_{2} + \cdots$ 的加法由逐项相加给出[13][35][36][37]： $(a_{0}+b_{0}) + (a_{1}+b_{1}) + (a_{2}+b_{2}) + \cdots $,或者用求和符号表示： $$ \sum_{k=0}^{\infty} a_{k} + \sum_{k=0}^{\infty} b_{k} = \sum_{k=0}^{\infty} (a_{k}+b_{k}).~ $$ 若用 $s_{a,n}$、$s_{b,n}$ 分别表示被相加的两个级数的部分和，用 $s_{a+b,n}$ 表示结果级数的部分和，那么根据定义可得：$s_{a+b,n} = s_{a,n} + s_{b,n}$.因此，结果级数的和，即其部分和序列的极限，满足： $$ \lim_{n \to \infty} s_{a+b,n} = \lim_{n \to \infty} (s_{a,n} + s_{b,n}) = \lim_{n \to \infty} s_{a,n} + \lim_{n \to \infty} s_{b,n},~ $$ 在极限存在的情况下。由此可见：如果两个级数都是可和的，那么它们的和也是可和的；结果级数的和等于两个原级数的和之和。两个发散级数的加法有时可能得到一个收敛级数：例如，将一个发散级数与其各项乘以 $-1$ 的级数相加，会得到一个全为零的级数，它收敛到 0。然而，如果两个级数中一个收敛、一个发散，那么它们的和必然发散。[35]

　　 对于实数级数或复数级数，级数加法是结合的、交换的和可逆的。因此，级数加法赋予实数或复数收敛级数集合以阿贝尔群的结构，同时也赋予所有实数或复数级数的集合（不论其收敛性如何）以阿贝尔群的结构。

数乘

　　 一个级数 $a_{0} + a_{1} + a_{2} + \cdots$ 与一个常数 $c$（在此情境下称为标量）的积，由逐项相乘给出[35]：$ca_{0} + ca_{1} + ca_{2} + \cdots $,或者用求和符号表示： $$ c \sum_{k=0}^{\infty} a_{k} \;=\; \sum_{k=0}^{\infty} ca_{k}.~ $$ 若用 $s_{a,n}$ 表示原级数的部分和，用 $s_{ca,n}$ 表示与标量 $c$ 相乘后的级数的部分和，那么根据定义有：$s_{ca,n} = c \, s_{a,n}, \quad \text{对所有 } n$.因此也有：$\lim_{n \to \infty} s_{ca,n} = c \, \lim_{n \to \infty} s_{a,n}$,在极限存在的情况下。由此可见：如果一个级数是可和的，那么它的任意非零标量倍数也是可和的；反之，如果一个级数是发散的，那么它的任意非零标量倍数也是发散的。

　　 实数和复数上的数乘运算是结合的、交换的、可逆的，并且对级数加法满足分配律。

　　 综上所述，级数的加法与数乘运算使得收敛级数集合以及实数级数集合构成了一个实向量空间。同理，对于复数级数与收敛复数级数，则得到复向量空间。这些向量空间都是无限维的。

级数的乘法

　　 两个级数 $a_{0} + a_{1} + a_{2} + \cdots \quad \text{与} \quad b_{0} + b_{1} + b_{2} + \cdots$ 相乘生成第三个级数 $c_{0} + c_{1} + c_{2} + \cdots$,这种乘法称为柯西乘积[12][13][14][36][38]。用求和符号表示为： $$ \Biggl(\sum_{k=0}^{\infty} a_{k}\Biggr) \cdot \Biggl(\sum_{k=0}^{\infty} b_{k}\Biggr) = \sum_{k=0}^{\infty} c_{k} = \sum_{k=0}^{\infty} \sum_{j=0}^{k} a_{j} b_{k-j},~ $$ 其中每个 $c_{k}$ 由下式给出：$c_{k} = \sum_{j=0}^{k} a_{j} b_{k-j} = a_{0} b_{k} + a_{1} b_{k-1} + \cdots + a_{k-1} b_{1} + a_{k} b_{0}.$ 在这里，结果级数 $c_{0} + c_{1} + c_{2} + \cdots$ 的部分和是否收敛，并不像加法那样容易判定。然而，如果两个级数 $a_{0} + a_{1} + a_{2} + \cdots \quad \text{与} \quad b_{0} + b_{1} + b_{2} + \cdots$ 都是绝对收敛的，那么它们的乘积级数也绝对收敛，其和等于原两个级数的和的乘积[13][36][39]： $$ \lim_{n \to \infty} s_{c,n} = \Bigl(\lim_{n \to \infty} s_{a,n}\Bigr) \cdot \Bigl(\lim_{n \to \infty} s_{b,n}\Bigr).~ $$ 对于实数或复数的绝对收敛级数，级数乘法是结合的、交换的，并且对级数加法满足分配律。因此，结合级数加法，级数乘法使得实数或复数的绝对收敛级数集合具有交换环的结构；再结合数乘，它们进一步构成交换代数的结构。同样，这些运算也使得所有实数或复数级数的集合具有结合代数的结构。

4. 数值级数的例子

圆周率 π

　　 $$ \sum_{n=1}^{\infty}\frac{1}{n^{2}}=\frac{1}{1^{2}}+\frac{1}{2^{2}}+\frac{1}{3^{2}}+\frac{1}{4^{2}}+\cdots = \frac{\pi^{2}}{6}~ $$ $$ \sum_{n=1}^{\infty}\frac{(-1)^{n+1}(4)}{2n-1}=\frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}+\frac{4}{13}-\cdots = \pi~ $$

自然对数 2

　　 $$ \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}=\ln 2~ $$ $$ \sum_{n=1}^{\infty}\frac{1}{2^{n}n}=\ln 2~ $$

自然对数底 e

　　 $$ \sum_{n=0}^{\infty}\frac{(-1)^{n}}{n!}=1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\cdots = \frac{1}{e}~ $$ $$ \sum_{n=0}^{\infty}\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\cdots = e~ $$

5. 收敛性检验

　　 最简单的级数收敛性检验之一，适用于所有级数，是 “消失条件” 或 **第 $n$ 项检验**： 如果 $\lim_{n \to \infty} a_{n} \neq 0$，那么该级数发散；如果 $\lim_{n \to \infty} a_{n} = 0$，那么该检验无法得出结论。【46】【47】

绝对收敛性检验

　　 当一个级数的每一项都是非负实数时，例如这些项是某个实数或复数级数的绝对值，那么其部分和序列就是单调不减的。因此，一个具有非负项的级数当且仅当其部分和序列有上界时才收敛。由此可见，为一个级数或其项的绝对值找到上界，是证明级数收敛或绝对收敛的有效方法【48】【49】【47】【50】。

　　 例如，级数 $1+\frac{1}{4}+\frac{1}{9}+\cdots+\frac{1}{n^{2}}+\cdots$ 是收敛的并且是绝对收敛的，因为对所有 $n \geq 2$，都有 $\frac{1}{n^{2}}\leq \frac{1}{n-1}-\frac{1}{n}$，而一个 “望远镜求和” 论证表明，这些非负上界项的部分和本身被 2 所有界【43】。该级数的确切值是 $\frac{1}{6}\pi^{2}$，参见巴塞尔问题。

　　 这种利用 “上界” 的策略构成了一般级数比较判别法的基础。首先是直接比较判别法【51】【52】【47】：对于任意级数 $\sum a_{n}$，如果存在一个绝对收敛的级数 $\sum b_{n}$，并且对某个正实数 $C$ 以及充分大的 $n$，满足 $|a_{n}| \leq C|b_{n}|$，那么 $\sum a_{n}$ 也绝对收敛。反之，如果 $\sum |b_{n}|$ 发散，并且对充分大的 $n$，满足 $|a_{n}| \geq |b_{n}|$，那么 $\sum a_{n}$ 也不绝对收敛（虽然它仍然可能条件收敛，例如当 $a_{n}$ 符号交替时）。其次是极限比较判别法【53】【54】：如果存在一个绝对收敛的级数 $\sum b_{n}$，并且对充分大的 $n$，满足 $\left|\frac{a_{n+1}}{a_{n}}\right| \leq \left|\frac{b_{n+1}}{b_{n}}\right|$，那么 $\sum a_{n}$ 也绝对收敛。反之，如果 $\sum |b_{n}|$ 发散，并且对充分大的 $n$，满足 $\left|\frac{a_{n+1}}{a_{n}}\right| \geq \left|\frac{b_{n+1}}{b_{n}}\right|$，那么 $\sum a_{n}$ 也不绝对收敛，尽管在 $a_{n}$ 符号变化时它仍可能条件收敛。

　　 通过将比较方法应用于几何级数【20】【21】，上述两类一般判别法又能推出两个更常见、且通常十分有用的收敛性检验，适用于非负项级数的收敛性，或一般项级数的绝对收敛性。比值判别法（比值审敛法）【55】【56】【57】：如果存在常数 $C < 1$，使得对充分大的 $n$，$\left|\frac{a_{n+1}}{a_{n}}\right| < C$，则 $\sum a_{n}$ 绝对收敛。当比值小于 1，但不能被限制在某个固定的 $C < 1$ 以内时，收敛性是可能的，但此判别法无法得出结论。根值判别法【55】【58】【59】：如果存在常数 $C < 1$，使得对充分大的 $n$，$|a_{n}|^{1/n} \leq C$，则 $\sum a_{n}$ 绝对收敛。

　　 另一种方法是利用与积分级数展开的比较，得出积分判别法【60】【61】：如果 $f(x)$ 是定义在区间 $[1,\infty)$ 上的正的单调递减函数，并且对所有 $n$ 有 $a_{n} = f(n)$，那么级数 $\sum a_{n}$ 收敛，当且仅当积分 $\int_{1}^{\infty} f(x)\,dx$ 有限。利用与 “压缩展开” 的级数比较，可以得到柯西凝缩判别法【29】【30】：如果数列 $\{a_{n}\}$ 非负且单调递减，那么级数 $\sum a_{n}$ 与 $\sum 2^{k} a_{(2^{k})}$ 要么同时收敛，要么同时发散。

条件收敛性检验

　　 一个实数或复数项级数，如果它是收敛的，但不是绝对收敛的，那么称它为条件收敛（或半收敛）。条件收敛的检验方式不同于绝对收敛。

　　 其中一个重要的条件收敛判别方法是交错级数判别法（又称莱布尼茨判别法）【62】【63】【64】：若级数具有如下形式 $\sum (-1)^{n} a_{n}$，并且所有 $a_{n} > 0$，则称为交错级数。这样的级数在数列 $\{a_{n}\}$ 单调递减且趋于 0 时收敛。反之，一般并不成立。一个著名的应用实例是交错调和级数： $$ \sum_{n=1}^{\infty} \frac{(-1)^{\,n+1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots ,~ $$ 该级数依照交错级数判别法收敛，并且其和等于 $\ln 2$。然而，如果取每项的绝对值，就得到普通的调和级数 $\sum_{n=1}^{\infty} \frac{1}{n}$，它是发散的【65】【66】。

　　 交错级数判别法可以看作是更一般的狄利克雷判别法的一个特例【67】【68】【69】： 如果数列 $(a_{n})$ 是一个单调递减的非负实数列，并且收敛于 0；而 $(\lambda_{n})$ 是另一个数列，其部分和有界，那么级数 $\sum \lambda_{n} a_{n}$ 收敛。取 $\lambda_{n} = (-1)^{n}$，就能得到交错级数判别法。

　　 阿贝尔判别法是处理半收敛级数的另一种重要技巧【67】【29】：如果一个级数的形式为 $ \sum a_{n} = \sum \lambda_{n} b_{n}$，其中，由 $b_{n}$ 构成的级数的部分和 $s_{b,n} = b_{0} + b_{1} + \cdots + b_{n}$ 是有界的，且 $\lambda_{n}$ 具有有界变差，并且 $\lim \lambda_{n} b_{n}$ 存在：$\sup_{n}|s_{b,n}| < \infty,\quad \sum |\lambda_{n+1} - \lambda_{n}| < \infty$，并且 $\lambda_{n} s_{b,n}$ 收敛，则级数 $\sum a_{n}$ 收敛。

　　 对于特定类型的级数，还有一些专门的收敛性检验方法，例如傅里叶级数的迪尼判别法【70】。

截断误差的估计

　　 在数值分析中（尤其是验证数值计算与计算机辅助证明中），级数的截断误差估计非常重要。它既可用于证明收敛性，也可用于分析收敛速度。

　　 交错级数

　　 当一个交错级数 $S := \sum_{m=0}^{\infty} (-1)^{m} u_{m}$ 满足交错级数判别法的条件时，可以得到精确的误差估计【71】：设部分和为 $s_{n} := \sum_{m=0}^{n} (-1)^{m} u_{m}$，则有不等式 $$ |S - s_{n}| \leq u_{n+1}.~ $$ 超几何级数

　　 利用比值判别法，可以得到超几何级数截断时的误差项估计【72】。

　　 矩阵指数

　　 矩阵指数定义为 $$ \exp\left(X\right) := \sum_{k=0}^{\infty} \frac{1}{k!} X^{k}, \quad X \in \mathbb{C}^{n \times n},~ $$ 在 “缩放与平方” 方法中，可以得到如下误差估计【73】【74】【75】： $$ T_{r,s}(X) := \Biggl( \sum_{j=0}^{r} \frac{1}{j!} \Bigl(X/s\Bigr)^{j} \Biggr)^{s},~ $$ 并且 $$ \bigl\| \exp\left(X\right) - T_{r,s}(X)\bigr\| \leq \frac{\|X\|^{r+1}}{s^{r}(r+1)!} \exp\left(\|X\|\right) .~ $$

6. 发散级数的求和

　　 在许多情况下，我们希望给那些严格意义上不收敛（其部分和数列不收敛）的级数赋予一个广义的和。所谓求和方法，就是以系统的方式将 “级数求和” 的经典概念推广到发散级数的一种方法。常见的求和方法包括：切萨罗求和、广义切萨罗 $(C,\alpha)$ 求和、阿贝尔求和以及博雷尔求和，其适用范围依次扩展到越来越 “发散” 的级数。这些方法都是基于对原级数项数列或其部分和数列的序列变换。另一类求和方法则基于解析延拓而不是序列变换。

　　 关于可能的可求和方法，人们已经知道一些一般性结论。例如，西尔弗曼–托普利茨定理刻画了矩阵求和方法，即通过将一个无限矩阵作用于系数向量来对发散级数求和的方法。而最一般的发散级数求和方法是非构造性的，涉及到巴拿赫极限。

7. 函数级数

　　 一个实值或复值函数的级数 $$ \sum_{n=0}^{\infty} f_{n}(x)~ $$ 若在集合 $E$ 上逐点收敛到某个极限函数 $f(x)$，则称该级数在 $E$ 上逐点收敛。也就是说，对于 $E$ 中的每一个 $x$，这个级数作为一个实数或复数级数是收敛的。 等价地，部分和 $$ s_{N}(x) = \sum_{n=0}^{N} f_{n}(x)~ $$ 当 $N \to \infty$ 时，对每一个 $x \in E$，收敛到 $f(x)$。

　　 比函数级数逐点收敛更强的一种收敛概念是一致收敛。如果一个级数在集合 $E$ 上逐点收敛到函数 $f(x)$，并且其第 $N$ 部分和对极限函数的逐点近似误差的上确界 $$ \sup_{x \in E} \, \bigl| s_{N}(x) - f(x) \bigr|~ $$ 随着 $N \to \infty$ 收敛到 0，且与 $x$ 的取值无关，那么称该级数在集合 $E$ 上一致收敛。一致收敛是函数级数中非常理想的性质，因为它能保证级数的许多性质在极限中得以保留。比如：如果一列连续函数的级数一致收敛，则其极限函数也是连续的。类似地，如果函数 $f_{n}$ 在某个有界闭区间 $I$ 上可积，并且它们一致收敛，那么该级数在 $I$ 上也可积，而且可以逐项积分。一致收敛的常见判别法包括：魏尔斯特拉斯 M 判别法、阿贝尔一致收敛判别法、迪尼判别法以及柯西判别准则。

　　 函数级数还可以定义更复杂的收敛类型。例如，在测度论中，如果一个函数级数在除了一个测度为零的集合之外的所有点上逐点收敛，则称其为几乎处处收敛。其他收敛方式则依赖于所考虑的函数空间上的不同度量结构。例如，一个函数级数在集合 $E$ 上均方收敛到极限函数 $f$，是指满足： $$ \lim_{N \to \infty} \int_{E} \bigl| s_{N}(x) - f(x) \bigr|^{2} \, dx = 0 .~ $$

幂级数

　　 幂级数是形如 $$ \sum_{n=0}^{\infty} a_{n}(x-c)^{n}.~ $$ 的级数。一个函数在点 $c$ 处的泰勒级数就是幂级数。在很多情况下，该级数在点 $c$ 的某个邻域内收敛于这个函数。举例来说，级数 $$ \sum_{n=0}^{\infty} \frac{x^{n}}{n!}~ $$ 是函数 $e^{x}$ 在原点处的泰勒级数，并且对任意实数或复数 $x$，它都收敛于 $e^{x}$。

　　 除非该级数仅在 $x=c$ 处收敛，否则它会在复平面上以 $c$ 为中心的某个收敛圆盘内收敛，并且可能在圆盘边界上的某些点也收敛。这个圆盘的半径称为收敛半径，原则上可以由系数 $a_{n}$ 的渐近行为来确定。在收敛圆盘内部的任意闭有界（即紧致）子集上，该级数都是一致收敛的，也就是说，它在紧集上是一致收敛的。

　　 从历史上看，像莱昂哈德·欧拉这样的数学家，往往自由地操作无穷级数，即便这些级数并不收敛。而当微积分在 19 世纪被严格地奠定在正确的基础上时，对级数收敛性的严格证明成为了必需。

形式幂级数

　　 虽然幂级数的许多应用都涉及其和，但也可以把幂级数当作形式和来处理。这意味着实际上并不进行加法运算，符号 “+” 只是一个抽象的连接符号，它不一定被解释为通常意义上的加法。在这种情况下，研究的对象是系数序列本身，而不是级数的收敛性。形式幂级数常用于组合数学中，用来描述和研究一些难以直接处理的数列，例如通过生成函数方法。希尔伯特–庞加莱级数就是一种形式幂级数，用来研究分次代数。

　　 即便不考虑幂级数的极限，只要项具有合适的代数结构，也可以 “形式化” 地定义加法、乘法、导数和反导数等运算，把符号 “+” 当作加法来使用。在最常见的情形下，各项属于一个交换环，因此形式幂级数可以逐项相加，并可通过柯西乘积来定义乘法。在这种情况下，形式幂级数代数就是底层项环上的自然数幺半群的整体代数【76】。如果底层项环是一个微分代数，那么形式幂级数代数也是一个微分代数，并且可以逐项进行求导。

洛朗级数

　　 洛朗级数是幂级数的推广，它允许在级数中同时包含负指数项和正指数项。因此，洛朗级数的形式为 $$ \sum_{n=-\infty}^{\infty} a_{n}x^{n}.~ $$ 如果这样的级数收敛，那么一般情况下，它是在一个环形区域（而不是圆盘）内收敛，并且可能在环形区域的某些边界点上也收敛。该级数在收敛环域内部的任意紧致子集上都是一致收敛的。

狄利克雷级数

　　 狄利克雷级数是形如 $$ \sum_{n=1}^{\infty} \frac{a_{n}}{n^{s}},~ $$ 的级数，其中 $s$ 是一个复数。

　　 例如，如果所有 $a_{n} = 1$，那么该狄利克雷级数就是黎曼ζ函数： $$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^{s}}.~ $$ 与 ζ 函数类似，狄利克雷级数在解析数论中普遍起着重要作用。一般来说，当 $\operatorname{Re}(s)$ 大于某个数（称为收敛线，abscissa of convergence）时，狄利克雷级数收敛。在许多情况下，狄利克雷级数可以通过解析延拓扩展到收敛域之外的区域。

　　 例如，ζ 函数的狄利克雷级数在 $\operatorname{Re}(s) > 1$ 时绝对收敛，但 ζ 函数可以解析延拓为在复平面 $\mathbb{C} \setminus \{1\}$ 上的全纯函数，并且在 $s=1$ 处有一个单极点。

　　 这种级数可以直接推广到更一般的广义狄利克雷级数。

三角级数

　　 项为三角函数的函数级数称为三角级数： $$ A_{0}+\sum_{n=1}^{\infty}\bigl(A_{n} \cos\left(nx\right) +B_{n} \sin\left(nx\right) \bigr).~ $$ 其中最重要的例子是函数的傅里叶级数。

渐近级数

　　 渐近级数（通常称为渐近展开）是由不同阶的渐近函数项组成的无穷级数，其部分和在某个渐近极限下可以近似某个函数。一般来说，渐近级数并不收敛，但它们作为一系列近似仍然非常有用——在有限项截断时，往往能给出与目标结果非常接近的数值。它们是微扰理论和算法分析中的关键工具。

　　 然而，与普通收敛函数级数不同，渐近级数通常不能在远离渐近极限的情况下任意提高精度。事实上，一个典型的渐近级数在远离渐近极限时，往往在有限项截断后达到最佳近似效果；如果继续加入更多项，反而会导致近似精度下降。

8. 无穷级数理论的历史

无穷级数的发展

　　 无穷级数在古希腊关于运动的哲学分析中发挥了重要作用，尤其体现在芝诺悖论中【77】。著名的 “阿基里斯与乌龟悖论” 表明，连续运动似乎需要无限多个时间瞬间，这在当时被认为是荒谬的：阿基里斯追赶乌龟，当他到达乌龟起跑时的位置时，乌龟已经移动到第二个位置；当他到达第二个位置时，乌龟又移动到第三个位置，如此往复。芝诺据说据此认为，阿基里斯永远不可能追上乌龟，因此连续运动不过是一种幻觉。芝诺将赛跑划分为无限多个子赛段，每一段都需要有限的时间，因此阿基里斯追上乌龟所需的总时间可以用一个级数表示。这个悖论在数学和想象层面的解决方案是：虽然该级数有无穷多项，但其和是有限的，这一有限和正好给出了阿基里斯追上乌龟所需的时间。然而，在现代运动哲学中，这个问题在物理层面依旧悬而未决。哲学家和物理学家都像芝诺一样，对空间运动是否可以无限可分持怀疑态度：在试图调和量子力学与广义相对论的量子引力理论中，常常引入普朗克尺度下的时空量子化设想【78】【79】。

　　 古希腊数学家阿基米德首次给出了无穷级数求和的实例，其方法在今天的微积分中仍被使用。他采用穷竭法通过无穷级数求和计算抛物线弧下的面积【5】，并给出了对 $\pi$ 的惊人精确的近似值【80】【81】。

　　 大约在公元 1350 年，喀拉拉学派的数学家也在研究无穷级数【82】。

　　 17 世纪，詹姆斯·格雷戈里利用新的十进制系统研究无穷级数，并发表了若干麦克劳林级数。1715 年，布鲁克·泰勒提出了一般方法，可以为所有存在泰勒展开的函数构造其泰勒级数。18 世纪时，莱昂哈德·欧拉发展了超几何级数和 q-级数理论。

收敛判别准则

　　 对无穷级数有效性的系统研究一般认为始于高斯在 19 世纪的工作。在此之前，欧拉已经研究过超几何级数 $$ 1+\frac{\alpha \beta}{1 \cdot \gamma}x + \frac{\alpha (\alpha + 1)\beta (\beta + 1)}{1 \cdot 2 \cdot \gamma (\gamma + 1)}x^{2} + \cdots~ $$ 而高斯在 1812 年发表了一篇论文，提出了更简明的收敛性判别准则，并讨论了余项问题及收敛范围。

　　 柯西（1821 年）坚持严格的收敛性检验；他证明了即使两个级数都收敛，它们的乘积也未必收敛，并由此开启了有效判别准则的发现。收敛与发散这两个术语早在格雷戈里（1668 年）时就已提出。欧拉和高斯曾给出过若干判别准则，而麦克劳林也曾预见到柯西的一些发现。柯西还通过将复函数展开为幂级数的形式，大大推动了幂级数理论的发展。

　　 阿贝尔（1826 年）在其关于二项式级数的论文中 $$ 1 + \frac{m}{1!}x + \frac{m(m-1)}{2!}x^{2} + \cdots~ $$ 修正了柯西的一些结论，并且对复数取值的 $m$ 和 $x$ 给出了完全科学的求和方法。他指出，在研究收敛性问题时，必须重视连续性的概念。

　　 柯西的方法导致的多是一些特殊而非普遍的判别准则。拉贝（1832 年）对该主题作了首次深入研究；德·摩根（自 1842 年起）提出了对数判别法，但杜布瓦–雷蒙（1873 年）和普林斯海姆（1889 年）证明其在某一区域内失效。此后还有贝特朗（1842 年）、博内（1843 年）、马尔姆斯滕（1846、1847 年，其中 1847 年的研究未用积分方法）、斯托克斯（1847 年）、保克尔（1852 年）、切比雪夫（1852 年）以及阿恩特（1853 年）的工作。

　　 一般性的判别准则始于库默尔（1835 年），此后由 艾森斯坦（1847 年）、魏尔斯特拉斯（在其函数论的多项贡献中）、迪尼（1867 年）、杜布瓦–雷蒙（1873 年）以及其他许多人进一步研究。普林斯海姆在 1889 年发表的论文中给出了当时最完整的一般理论。

一致收敛

　　 一致收敛理论最早由 **柯西**（1821 年）提出，但其局限性被 **阿贝尔**指出。首次成功解决这一问题的是 **塞德尔**与 **斯托克斯**（1847–48 年）。柯西在 1853 年再次处理该问题，承认了阿贝尔的批评，并得出了与斯托克斯相同的结论。**托马**（1866 年）使用过这一理论，但尽管函数论的需求不断增加，人们在认识到区分一致收敛与非一致收敛的重要性方面仍存在很大延误。

半收敛

　　 如果一个级数是收敛的，但不是绝对收敛的，那么称其为半收敛（或条件收敛）。

　　 半收敛级数由 泊松（1823 年）研究过，他还给出了麦克劳林公式余项的一般形式。然而，最重要的解决方案来自雅可比（1834 年），他从不同的角度处理余项问题，得到了另一种公式。马尔姆斯滕（1847 年）对其进行了进一步推导并给出了另一表达式。施勒米尔希（Zeitschrift, 第 1 卷，第 192 页，1856 年）也改进了雅可比的余项，并展示了余项与伯努利函数 $$ F(x) = 1^{n} + 2^{n} + \cdots + (x-1)^{n}~ $$ 之间的关系。

　　 热诺基（1852 年）也对该理论作出了贡献。

　　 早期的研究者中还有弗龙斯基，他的 “最高法则”（loi suprême，1815 年）几乎无人理会，直到凯莱（1873 年）才使之受到重视。

傅里叶级数

　　 在高斯、阿贝尔和柯西研究无穷级数理论的同时，傅里叶级数也因物理学的考虑而受到研究。关于正弦和余弦展开、倍角展开成正弦与余弦幂的级数，早在维达时代就已经被研究过，之后由雅各布·伯努利（1702 年）与其兄约翰·伯努利（1701 年）处理过。后来，欧拉与拉格朗日简化了相关内容，普安索、施勒特、格莱舍与库默尔也作出了贡献。

　　 傅里叶（1807 年）提出了一个不同的问题：把一个给定的函数 $x$ 展开成关于 $x$ 倍角的正弦或余弦的级数。他将这一问题系统化，写入了其著作《热的解析理论（1822）。欧拉早已给出了求解级数系数的公式，而傅里叶是第一个提出并尝试证明这一 一般性定理的人。泊松（1820–23 年）也从不同的角度研究了这一问题。然而，傅里叶并没有解决其级数收敛性的问题，这一问题由柯西（1826 年）首先尝试处理，并由狄利克雷（1829 年）以彻底科学的方法加以解决（参见傅里叶级数的收敛性）。狄利克雷在 Crelle（1829 年）上发表的关于三角级数的研究，后来受到黎曼（1854 年）、海涅、利普希茨、施莱夫利与杜布瓦–雷蒙的批评与改进。其他对三角级数与傅里叶级数理论作出突出贡献的学者还包括迪尼、埃尔米特、阿尔芬、克劳泽、拜尔利以及阿佩尔。

9. 一般指标集上的求和

　　 可以对任意指标集 $I$ 定义无穷求和【83】。这种推广与通常的级数概念相比有两个主要区别：指标集 $I$ 上可能没有给定特定的顺序；指标集 $I$ 可能是不可数的。因此，需要重新考虑收敛性的概念，因为例如条件收敛的概念就依赖于指标集的顺序。

　　 如果 $a: I \mapsto G$ 是从指标集 $I$ 到某个集合 $G$ 的函数，那么与 $a$ 相关的 “级数” 就是对所有 $x \in I$ 的元素 $a(x) \in G$ 的形式和，记作 $$ \sum_{x \in I} a(x).~ $$ 当指标集是自然数集 $I = \mathbb{N}$ 时，函数 $a: \mathbb{N} \mapsto G$ 就是一个数列，记作 $a(n) = a_{n}$。在这种情况下，以自然数为指标的级数就是一个有序的形式和，因此我们把 $\sum_{n \in \mathbb{N}}$ 改写为 $\sum_{n=0}^{\infty}$ 以强调自然数所诱导的顺序。由此得到常见的记号： $$ \sum_{n=0}^{\infty} a_{n} = a_{0} + a_{1} + a_{2} + \cdots .~ $$

非负数族

　　 当在指标集 $I$ 上对一族非负实数 $\{a_{i}: i \in I\}$ 求和时，定义为 $$ \sum_{i \in I} a_{i} \;=\; \sup \Biggl\{ \sum_{i \in A} a_{i} : A \subseteq I, \, A \text{ finite} \Biggr\} \;\in\; [0, +\infty].~ $$ 任何对非负实数的求和，都可以理解为相应非负函数在计数测度下的积分，这也解释了这两种构造之间的许多相似之处。

　　 当上确界是有限值时，集合 $\{i \in I : a_{i} > 0\}$ 必然是可数的。确实，对于每个 $n \geq 1$，集合 $A_{n} = \{i \in I : a_{i} > 1/n\}$ 的基数 $|A_{n}|$ 是有限的，因为 $$ \frac{1}{n}\,|A_{n}| = \sum_{i \in A_{n}} \frac{1}{n} \;\leq\; \sum_{i \in A_{n}} a_{i} \;\leq\; \sum_{i \in I} a_{i} \;<\; \infty.~ $$ 因此，集合 $A = \{i \in I : a_{i} > 0\} \;=\; \bigcup_{n=1}^{\infty} A_{n}$ 是可数的。

　　 如果 $I$ 是可数无限集，并被枚举为 $I = \{i_{0}, i_{1}, \ldots\}$，

　　 那么上述定义的求和满足 $$ \sum_{i \in I} a_{i} = \sum_{k=0}^{\infty} a_{i_{k}},~ $$ 前提是允许该级数的和取值为 $\infty$。

阿贝尔拓扑群

　　 设 $a: I \to X$ 是从某个非空集合 $I$ 映射到豪斯多夫阿贝尔拓扑群 $X$ 的一个映射，也记作 $(a_{i})_{i \in I}$.设 $\operatorname{Finite}(I)$ 为 $I$ 的所有有限子集的集合，将 $\operatorname{Finite}(I)$ 看作一个有向集，其顺序由包含关系 $\subseteq$ 给定，并且并集作为其并算子。若下述极限在 $X$ 中存在，则称族 $(a_{i})_{i \in I}$ 无条件可和，并将其和记作 $$ \sum_{i \in I} a_{i} \;:=\; \lim_{A \in \operatorname{Finite}(I)} \sum_{i \in A} a_{i} = \lim \Biggl\{ \sum_{i \in A} a_{i} : A \subseteq I, \, A \text{ finite} \Biggr\}.~ $$ 说 $S := \sum_{i \in I} a_{i}$ 是有限部分和的极限，意味着：对 $X$ 中原点的任意邻域 $V$，都存在一个有限子集 $A_{0} \subseteq I$，使得对任意有限超集 $A \supseteq A_{0}$，都有 $$ S - \sum_{i \in A} a_{i} \in V.~ $$ 由于 $\operatorname{Finite}(I)$ 并不是全序集，因此这里的极限并不是部分和序列的极限，而是一个网的极限【84】【85】。

　　 对于 $X$ 中原点的任意邻域 $W$，都存在一个更小的邻域 $V$，使得 $V - V \subseteq W$.由此可得，一个无条件可和族 $(a_{i})_{i \in I}$ 的有限部分和构成一个柯西网。也就是说，对于 $X$ 中原点的任意邻域 $W$，存在 $I$ 的一个有限子集 $A_{0}$，使得 $$ \sum_{i \in A_{1}} a_{i} - \sum_{i \in A_{2}} a_{i} \in W \quad \text{对所有有限超集 } A_{1}, A_{2} \supseteq A_{0} \text{ 都成立},~ $$ 这进一步推出：对每个 $i \in I \setminus A_{0}$，有 $a_{i} \in W$（取 $A_{1} := A_{0} \cup \{i\}$，$A_{2} := A_{0}$ 即可）。

　　 当 $X$ 是完备空间时，族 $(a_{i})_{i \in I}$ 在 $X$ 中无条件可和，当且仅当其有限和满足上述柯西网条件。并且，当 $X$ 是完备空间且 $(a_{i})_{i \in I}$ 在 $X$ 中无条件可和时，任意子集 $J \subseteq I$ 的子族 $(a_{j})_{j \in J}$ 也在 $X$ 中无条件可和。

　　 当非负数族的和（以前面所定义的扩展意义）是有限时，它与拓扑群 $X = \mathbb{R}$ 中的和一致。

　　 如果拓扑群 $X$ 中的族 $(a_{i})_{i \in I}$ 是无条件可和的，那么对于 $X$ 中原点的任意邻域 $W$，存在一个有限子集 $A_{0} \subseteq I$，使得对所有 $i \notin A_{0}$，都有 $a_{i} \in W$.如果 $X$ 是第一可数空间，那么由此推出集合 $\{i \in I : a_{i} \neq 0\}$ 是可数的。但在一般的阿贝尔拓扑群中，这个结论并不一定成立（见下例）。

无条件收敛级数

　　 设 $I = \mathbb{N}$。如果一个族 $\{a_{n}, n \in \mathbb{N}\}$ 在豪斯多夫阿贝尔拓扑群 $X$ 中无条件可和，那么该级数在通常意义下收敛，并且其和相同： $$ \sum_{n=0}^{\infty} a_{n} \;=\; \sum_{n \in \mathbb{N}} a_{n}.~ $$ 根据定义，无条件可和性本质上与求和的顺序无关。当 $\sum a_{n}$ 无条件可和时，对指标集 $\mathbb{N}$ 的任意排列 $\sigma : \mathbb{N} \to \mathbb{N}$，该级数依然收敛，且和保持不变： $$ \sum_{n=0}^{\infty} a_{\sigma(n)} \;=\; \sum_{n=0}^{\infty} a_{n}.~ $$ 反之，如果一个级数 $\sum a_{n}$ 在任意排列下都收敛，则它是无条件收敛的。

　　 当 $X$ 是完备空间时，无条件收敛也等价于其所有子级数都收敛；若 $X$ 是巴拿赫空间，则这一条件又等价于：对任意符号序列 $\varepsilon_{n} = \pm 1$，级数 $$ \sum_{n=0}^{\infty} \varepsilon_{n} a_{n}~ $$ 在 $X$ 中收敛。

拓扑向量空间中的级数

　　 若 $X$ 是一个**拓扑向量空间**（TVS），而 $(x_{i})_{i \in I}$ 是 $X$ 中的一个（可能不可数的）族，那么当网 $(x_{A})_{A \in \operatorname{Finite}(I)}$ 在 $X$ 中有极限时，称该族是可和的【86】。其中，$\operatorname{Finite}(I)$ 是由包含关系 $\subseteq$ 诱导的有向集，表示 $I$ 的所有有限子集，并且 $x_{A} := \sum_{i \in A} x_{i}$.

　　 如果此外还满足：对 $X$ 上的任意连续半范数 $p$，族 $(p(x_{i}))_{i \in I}$ 也是可和的，那么称该族是绝对可和的。若 $X$ 是一个可赋范空间，并且 $(x_{i})_{i \in I}$ 在 $X$ 中绝对可和，那么除至多可数多个 $x_{i}$ 外，其余全为零。因而，在赋范空间中，通常只需考虑项数可数的级数。

　　 可和族在核空间理论中起着重要作用。

巴拿赫空间与半赋范空间中的级数

　　 级数的概念可以容易地推广到半赋范空间的情形。若 $(x_{n})$ 是赋范空间 $X$ 中的一个序列，且 $x \in X$，则当该级数的部分和序列 $\Bigl(\sum_{n=0}^{N} x_{n}\Bigr)_{N=1}^{\infty}$ 在 $X$ 中收敛到 $x$ 时，称级数 $\sum x_{n}$ 在 $X$ 中收敛到 $x$。换句话说：$\Bigl\|x - \sum_{n=0}^{N} x_{n}\Bigr\| \;\to\; 0 \quad \text{当 } N \to \infty$.

　　 更一般地，在任意阿贝尔豪斯多夫拓扑群中都可以定义级数的收敛性。具体而言，若部分和序列收敛到 $x$，则称级数 $\sum x_{n}$ 收敛到 $x$。

　　 若 $(X, |\cdot|)$ 是一个半赋范空间，则绝对收敛的概念为：向量级数 $\sum_{i \in I} x_{i}$ 在 $X$ 中绝对收敛，当且仅当 $$ \sum_{i \in I} |x_{i}| < +\infty,~ $$ 此时除了至多可数个 $|x_{i}|$ 外，其余必为零。

　　 在巴拿赫空间中，如果一个可数向量级数绝对收敛，则它一定无条件收敛；但反之仅在有限维巴拿赫空间中成立（Dvoretzky–Rogers 定理，1950）。

良序求和

　　 若指标集 $I$ 是一个良序集，例如一个序数 $\alpha_{0}$，则可以讨论条件收敛级数。在这种情况下，利用超限递归定义：对于后继序数 $\alpha+1$，有 $$ \sum_{\beta < \alpha+1} a_{\beta} \;=\; a_{\alpha} + \sum_{\beta < \alpha} a_{\beta}.~ $$ 对于极限序数 $\alpha$，定义为 $$ \sum_{\beta < \alpha} a_{\beta} \;=\; \lim_{\gamma \to \alpha} \sum_{\beta < \gamma} a_{\beta},~ $$ 如果该极限存在的话。若所有小于等于 $\alpha_{0}$ 的极限都存在，则称该级数收敛。

例子

10. 参见

11. 注释

  1. Thompson, Silvanus; Gardner, Martin (1998). Calculus Made Easy. Macmillan. ISBN 978-0-312-18548-0.
  2. Huggett, Nick (2024), "Zeno's Paradoxes", in Zalta, Edward N.; Nodelman, Uri (eds.), *The Stanford Encyclopedia of Philosophy* (Spring 2024 ed.), Metaphysics Research Lab, Stanford University, 取自 2024-03-25
  3. Apostol 1967, 第 374–375 页
  4. Swain, Gordon; Dence, Thomas (1998). "Archimedes' Quadrature of the Parabola Revisited". *Mathematics Magazine*. 71 (2): 123–130. doi:10.2307/2691014. ISSN 0025-570X. JSTOR 2691014.
  5. Russo, Lucio (2004). *The Forgotten Revolution*. Silvio Levy 译. 德国: Springer-Verlag. 第 49–52 页. ISBN 978-3-540-20396-4.
  6. Apostol 1967, 第 377 页
  7. Apostol 1967, 第 378 页
  8. Apostol 1967, 第 37 页
  9. Spivak 2008, 第 471–472 页
  10. Apostol 1967, 第 384 页
  11. Ablowitz, Mark J.; Fokas, Athanassios S. (2003). Complex Variables: Introduction and Applications (第 2 版). Cambridge University Press. 第 110 页. ISBN 978-0-521-53429-1.
  12. Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra* (第 3 版). Hoboken, NJ: John Wiley and Sons. 第 238 页. ISBN 978-0-471-43334-7.
  13. Spivak 2008, 第 486–487, 493 页
  14. Wilf, Herbert S. (1990). Generatingfunctionology. San Diego: Academic Press. 第 27–28 页. ISBN 978-1-48-324857-8.
  15. Swokoski, Earl W. (1983). Calculus with Analytic Geometry (增订版). Boston: Prindle, Weber & Schmidt. 第 501 页. ISBN 978-0-87150-341-1.
  16. Rudin 1976，第 59 页
  17. Spivak 2008，第 426 页
  18. Apostol 1967，第 281 页
  19. Rudin 1976，第 63 页
  20. Spivak 2008，第 473–478 页
  21. Apostol 1967，第 388–390, 399–401 页
  22. Rudin 1976，第 61 页
  23. Spivak 2008，第 453 页
  24. Knuth, Donald E. (1992). "Two Notes on Notation". *American Mathematical Monthly*. 99 (5): 403–422. doi:10.2307/2325085. JSTOR 2325085.
  25. Atkinson, Kendall E. (1989). *An Introduction to Numerical Analysis* (第 2 版). New York: Wiley. 第 20 页. ISBN 978-0-471-62489-9. OCLC 803318878.
  26. Stoer, Josef; Bulirsch, Roland (2002). *Introduction to Numerical Analysis* (第 3 版). Princeton, N.J.: Recording for the Blind & Dyslexic. OCLC 50556273.
  27. Wilkins, David (2007). "Section 6: The Extended Real Number System" (PDF). maths.tcd.ie. 取自 2019-12-03.
  28. Kifowit, Steven J.; Stamps, Terra A. (2006). "The harmonic series diverges again and again" (PDF). *American Mathematical Association of Two-Year Colleges Review*. 27 (2): 31–43.
  29. Spivak 2008，第 496 页
  30. Rudin 1976，第 61 页
  31. Spivak 2008，第 483–486 页
  32. Apostol 1967，第 412–414 页
  33. Rudin 1976，第 76 页
  34. Spivak 2008，第 482 页
  35. Apostol 1967，第 385–386 页
  36. Saff, E. B.; Snider, Arthur D. (2003). *Fundamentals of Complex Analysis* (第 3 版). Pearson Education. 第 247–249 页. ISBN 0-13-907874-6.
  37. Rudin 1976，第 72 页
  38. Rudin 1976，第 73 页
  39. Rudin 1976，第 74 页
  40. Apostol 1967，第 384 页
  41. Apostol 1967，第 403–404 页
  42. Apostol 1967，第 386 页
  43. Apostol 1967，第 387 页
  44. Apostol 1967，第 396 页
  45. Gasper, G., Rahman, M. (2004). Basic Hypergeometric Series. Cambridge University Press.
  46. Spivak 2008，第 473 页
  47. Rudin 1976，第 60 页
  48. Apostol 1967，第 381, 394–395 页
  49. Spivak 2008，第 457, 473–474 页
  50. Rudin 1976，第 71–72 页
  51. Apostol 1967，第 395–396 页
  52. Spivak 2008，第 474–475 页
  53. Apostol 1967，第 396 页
  54. Spivak 2008，第 475–476 页
  55. Apostol 1967，第 399–401 页
  56. Spivak 2008，第 476–478 页
  57. Rudin 1976，第 66 页
  58. Spivak 2008，第 493 页
  59. Rudin 1976，第 65 页
  60. Apostol 1967，第 397–398 页
  61. Spivak 2008，第 478–479 页
  62. Apostol 1967，第 403–404 页
  63. Spivak 2008，第 481 页
  64. Rudin 1976，第 71 页
  65. Apostol 1967，第 413–414 页
  66. Spivak 2008，第 482–483 页
  67. Apostol 1967，第 407–409 页
  68. Spivak 2008，第 495 页
  69. Rudin 1976，第 70 页
  70. Spivak 2008，第 524 页
  71. 正项与负项：交错级数
  72. Johansson, F. (2016). Computing hypergeometric functions rigorously. arXiv 预印本 arXiv:1606.06977.
  73. Higham, N. J. (2008). Functions of Matrices: Theory and Computation. Society for Industrial and Applied Mathematics.
  74. Higham, N. J. (2009). The scaling and squaring method for the matrix exponential revisited. SIAM Review, 51(4), 747–764.
  75. How and How Not to Compute the Exponential of a Matrix*
  76. Nicolas Bourbaki (1989). Algebra. Springer: §III.2.11.
  77. Huggett, Nick (2024). "Zeno's Paradoxes", 收录于 Zalta, Edward N.; Nodelman, Uri (编), The Stanford Encyclopedia of Philosophy* (2024 春季版), Metaphysics Research Lab, Stanford University, 检索于 2024-03-25.
  78. Snyder, H. (1947). "Quantized space-time". Physical Review, 67 (1): 38–41. Bibcode:1947PhRv...71...38S, doi:10.1103/PhysRev.71.38.
  79. "The Unraveling of Space-Time". *Quanta Magazine*. 2024-09-25. 检索于 2024-10-11.
  80. O'Connor, J.J.; Robertson, E.F. (1996). "A history of calculus". University of St Andrews. 检索于 2007-08-07.
  81. Bidwell, James K. (1993-11-30). "Archimedes and Pi-Revisited". School Science and Mathematics. 94 (3): 127–129. doi:10.1111/j.1949-8594.1994.tb15638.x.
  82. "Indians predated Newton 'discovery' by 250 years". manchester.ac.uk.
  83. Jean Dieudonné. Foundations of Mathematical Analysis. Academic Press
  84. Bourbaki, Nicolas (1998). General Topology: Chapters 1–4. Springer. 第 261–270 页. ISBN 978-3-540-64241-1.
  85. Choquet, Gustave (1966). Topology. Academic Press. 第 216–231 页. ISBN 978-0-12-173450-3.
  86. Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. Graduate Texts in Mathematics. 第 8 卷 (第 2 版). New York, NY: Springer. 第 179–180 页. ISBN 978-1-4612-7155-0.

12. 延伸阅读

13. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利