介值定理(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。
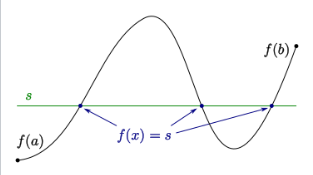
在数学分析中,中值定理指出:如果函数 $f$ 是一个连续函数,且其定义域包含区间 $[a, b]$,那么对于任意介于 $f(a)$ 与 $f(b)$ 之间的值,函数 $f$ 在该区间内至少有一个点取到这个值。
该定理有两个重要的推论:
- 如果一个连续函数在某个区间内的两个端点处函数值符号相反,那么它在这个区间内至少有一个零点(即有解)——这被称为波尔查诺定理 \(^\text{[1][2]}\)。
- 一个连续函数在一个区间上的值域本身也是一个区间。
1. 动机
这揭示了实数上连续函数的一个直观性质:设 $f$ 是定义在区间 $[1, 2]$ 上的连续函数,且已知 $f(1) = 3$、$f(2) = 5$,那么函数图像 $y = f(x)$ 在 $x$ 从 1 变到 2 的过程中,必定会穿过水平直线 $y = 4$。这表达了一个概念:在闭区间上的连续函数的图像可以不抬笔地画出来。
2. 定理
介值定理表述如下:
设实数集合 $\mathbb{R}$ 上的闭区间 $I = [a, b]$,函数 $f: I \to \mathbb{R}$ 连续,则有:
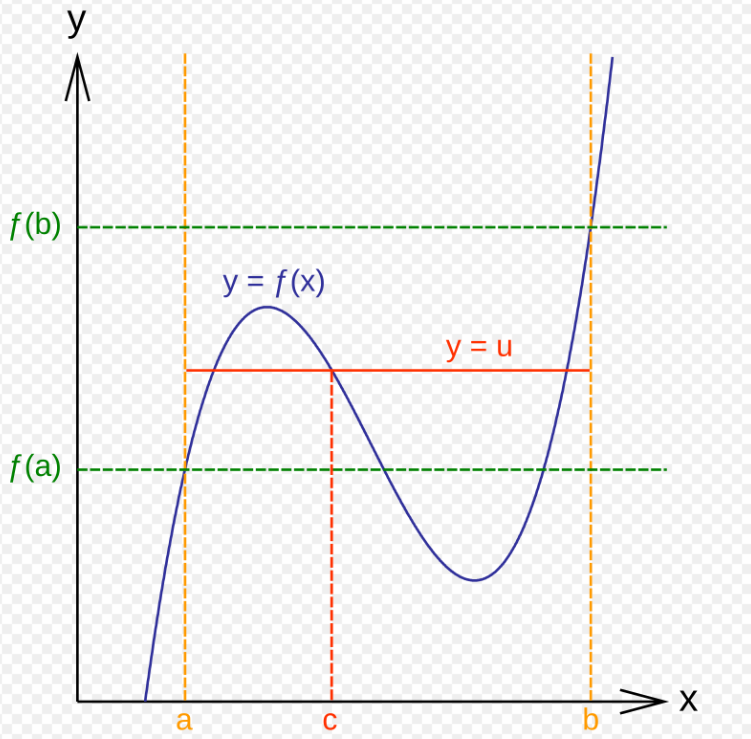
- 版本一:如果某个数 $u$ 介于 $f(a)$ 和 $f(b)$ 之间,即 $$ \min(f(a), f(b)) < u < \max(f(a), f(b)),~ $$ 那么存在某个点 $c \in (a, b)$,使得 $f(c) = u$.
- 版本二:函数值的集合 $f(I)$ 也是一个闭区间,且包含区间 $$ [\min(f(a), f(b)), \max(f(a), f(b))].~ $$
备注:版本二说明函数值的集合中不存在间断。对于任意两个函数值 $c, d \in f(I)$,若 $c < d$,则所有处于区间 $[c, d]$ 中的数也都是函数值,即 $$ [c, d] \subseteq f(I).~ $$ 在实数集合中,没有内部间隙的子集就是一个区间。版本一是版本二的一个特殊情况。
3. 与完备性的关系
介值定理依赖于实数的完备性,并且与之等价。该定理不适用于有理数集 $\mathbb{Q}$,因为有理数之间存在 “空隙”;这些空隙正是由无理数填补的。
例如,函数 $f(x) = x^2$ 在有理数域 $x \in \mathbb{Q}$ 上满足 $f(0) = 0, \quad f(2) = 4$ 但不存在一个有理数 $x$,使得 $f(x) = 2$ 因为 $\sqrt{2}$ 是一个无理数。
尽管如此,在实闭域上,仍然存在一种适用于多项式的介值定理形式,可参见魏尔斯特拉斯零点定理。
4. 证明
证明版本 A
该定理可以作为实数完备性的一个推论来证明,如下所示:\(^\text{[3]}\)
我们将证明第一种情况:$f(a) < u < f(b)$ 第二种情况的证明是类似的。
设 $$ S = \{x \in [a, b] \mid f(x) < u\}~ $$ 由于 $f(a) < u$,所以 $a \in S$,因此 $S$ 非空。又因为 $S \subseteq [a, b]$,所以它有上界 $b$。根据实数的完备性,集合 $S$ 的上确界 $c = \sup S$ 存在。也就是说,$c$ 是大于或等于 $S$ 中所有元素的最小实数。
注意,由于 $f$ 在 $a$ 处连续,我们可以通过让 $x$ 足够接近 $a$,使得 $f(x)$ 与 $f(a)$ 的差小于任意指定的 $\varepsilon > 0$。既然 $f(a) < u$ 是一个严格不等式,我们可以取 $$ \varepsilon = u - f(a) > 0~ $$ 根据连续性的定义,存在 $\delta > 0$,使得对所有 $x \in [a, b]$,只要 $$ |x - a| < \delta~ $$ 就有 $$ |f(x) - f(a)| < u - f(a) \Rightarrow f(x) < u~ $$ 考虑区间 $$ I_1 = [a, \min(a + \delta, b))~ $$ 注意到 $I_1 \subseteq [a, b]$,并且对所有 $x \in I_1$,都有 $|x - a| < \delta$,因此 $f(x) < u$。这说明在 $a$ 附近存在比 $a$ 更大的属于 $S$ 的点,所以 $c \ne a$。
同理,由于函数 $f$ 在点 $b$ 处是连续的,我们可以通过令 $x$ 足够接近 $b$,使 $f(x)$ 与 $f(b)$ 的差小于任意给定的 $\varepsilon > 0$。由于 $u < f(b)$ 是一个严格不等式,当我们取 $\varepsilon$ 为 $u$ 与 $f(b)$ 之间的距离时,可以得出类似的推论:所有足够接近 $b$ 的 $x$,都有 $f(x) > u$,这说明存在小于 $b$ 的一些数是集合 $S$ 的上界。更详细的证明如下:
取 $\varepsilon = f(b) - u > 0$,那么存在 $\delta > 0$,使得对所有 $x \in [a, b]$,若 $|x - b| < \delta$,则 $$ |f(x) - f(b)| < f(b) - u \Rightarrow f(x) > u~ $$
考虑区间: $$ I_2 = (\max(a, b - \delta), b]~ $$ 注意到 $I_2 \subseteq [a, b]$,并且其中每个 $x \in I_2$ 都满足 $|x - b| < \delta$,所以对于所有 $x \in I_2$,都有 $f(x) > u$。因此 $c \neq b$。 由于 $c \neq a$ 且 $c \neq b$,我们有 $c \in (a, b)$。现在我们要证明: $$ f(c) = u~ $$ 固定任意 $\varepsilon > 0$。由于 $f$ 在 $c$ 处连续,存在 $\delta_1 > 0$,使得对所有 $x \in [a, b]$,若 $|x - c| < \delta_1$,则: $$ |f(x) - f(c)| < \varepsilon~ $$ 又因为 $c \in (a, b)$,而开区间 $(a, b)$ 是开集,存在 $\delta_2 > 0$,使得: $$ (c - \delta_2, c + \delta_2) \subseteq (a, b)~ $$ 令 $\delta = \min(\delta_1, \delta_2)$,那么对于所有 $x \in (c - \delta, c + \delta)$,有: $$ f(x) - \varepsilon < f(c) < f(x) + \varepsilon~ $$ 根据上确界的性质,存在 $a^* \in (c - \delta, c] \subseteq S$,因此: $$ f(c) < f(a^*) + \varepsilon < u + \varepsilon~ $$ 再取 $a^{**} \in (c, c + \delta)$,因为 $c = \sup S$,所以 $a^{**} \notin S$,这意味着: $$ f(c) > f(a^{**}) - \varepsilon \geq u - \varepsilon~ $$ 综上,两个不等式成立: $$ u - \varepsilon < f(c) < u + \varepsilon~ $$ 对于所有 $\varepsilon > 0$ 都成立。因此我们推得:$f(c) = u$ 这是唯一可能的取值,正如定理所述。
证明 B 版本
我们只证明 $f(a) < u < f(b)$ 的情形,另一种 $f(a) > u > f(b)$ 的情形类似 \(^\text{[4]}\)。
定义函数 $g(x) = f(x) - u$,即 $f(x) = g(x) + u$。这样,原本的 $f(a) < u < f(b)$ 可以重写为 $g(a) < 0 < g(b)$,我们需要证明存在某个 $c \in [a, b]$,使得 $g(c) = 0$,这在直观上更容易理解。
进一步定义集合:
$$ S = \{x \in [a, b] : g(x) \leq 0\}~ $$
因为 $g(a) < 0$,所以 $a \in S$,即 $S$ 非空。此外,由于 $S \subseteq [a, b]$,它有上界,因此根据实数的完备性,最小上界 $c = \sup(S)$ 存在。
接下来我们讨论 $g(c)$ 的三个可能取值:$g(c) < 0$、$g(c) > 0$ 和 $g(c) = 0$。
假设反证法一:假设 $g(c) < 0$。根据连续性的定义,令 $\varepsilon = 0 - g(c) > 0$,存在 $\delta > 0$,使得: $$ x \in (c - \delta, c + \delta) \Rightarrow |g(x) - g(c)| < -g(c) \Rightarrow g(x) < 0~ $$ 取 $x = c + \delta/N$,其中 $N > \frac{\delta}{b - c} + 1$,由于 $1 < N$,有 $x < c + \delta$,从而: $$ g(x) < 0,\quad c < x < b \Rightarrow x \in S~ $$ 这说明 $x$ 是 $S$ 的一个上界,但 $x > c$,这与 $c$ 是最小上界矛盾。因此,$g(c) \geq 0$。
假设反证法二:假设 $g(c) > 0$。令 $\varepsilon = g(c) - 0 > 0$,存在 $\delta > 0$,使得: $$ x \in (c - \delta, c + \delta) \Rightarrow |g(x) - g(c)| < g(c)~ $$ 即: $$ -g(c) < g(x) - g(c) < g(c) \Rightarrow g(x) > 0~ $$ 若取 $x = c - \delta/2$,则有 $g(x) > 0$ 且 $a < x < c$,即 $x$ 是 $S$ 的一个上界,但 $x < c$,这又与 $c$ 是最小上界矛盾。因此,$g(c) > 0$ 不成立。 综上两种假设均被排除,唯一可能的情况是: $$ g(c) = 0 \Rightarrow f(c) = u~ $$ 备注:介值定理也可以使用非标准分析的方法来证明,非标准分析将涉及无穷小量的 “直观” 论证建立在严格的数学基础之上 \(^\text{[5]}\)。
5. 历史
该定理的某种形式早在公元前 5 世纪就已被提出,当时赫拉克利亚的布律松在研究化圆为方问题时使用了类似的思路。布律松认为,既然存在比一个给定正方形大的圆和比它小的圆,那么必然存在一个与该正方形面积相等的圆 \(^\text{[6]}\)。这个定理首次被贝尔纳·玻尔查诺于 1817 年严格证明。玻尔查诺采用了如下形式的表述 \(^\text{[7]}\):
设函数 $f$、$\varphi$ 在区间 $[\alpha, \beta]$ 上连续,且满足:$f(\alpha) < \varphi(\alpha), \quad f(\beta) > \varphi(\beta)$ 那么存在某个 $x \in (\alpha, \beta)$,使得:$f(x) = \varphi(x)$ 将 $\varphi$ 取为适当的常值函数,可以看出上述表述与现代的介值定理是等价的。
奥古斯丁-路易·柯西于 1821 年给出了现代表述及其证明 \(^\text{[8]}\)。两人都受到约瑟夫-路易·拉格朗日致力于形式化函数分析的思想启发。
认为连续函数具有介值性质这一思想更早可以追溯。西蒙·斯特文曾经对多项式函数(例如三次函数)证明了介值定理,他的方法是通过一个构造十进制解的算法:该算法将区间等分为 10 份,每次迭代产生一个新的小数位 \(^\text{[9]}\)。
在 “连续性” 这一概念被正式定义之前,介值性质曾被直接作为 “连续函数” 的定义条件之一。例如,路易·阿尔博加斯特就将连续函数定义为:没有跳跃、满足介值性质,并且增量的大小与自变量的增量成比例 \(^\text{[10]}\)。
更早期的作者普遍认为该结论是直观显然的,不需要证明。玻尔查诺和柯西的洞察在于:他们首次给出了通用的连续性定义(玻尔查诺基于实数的不等式,柯西基于无穷小),并据此提供了严格的证明。
6. 反命题不成立
达布函数是指具有 “介值性质” 的实值函数,即满足介值定理结论的函数:对于定义域中任意两个值 $a$ 和 $b$,以及介于 $f(a)$ 与 $f(b)$ 之间的任意数 $y$,总存在某个 $c \in (a, b)$ 使得 $f(c) = y$。
介值定理断言:每个连续函数都是达布函数。但并非每个达布函数都是连续函数,也就是说,介值定理的逆命题是不成立的。
举个例子,定义函数: $$ f : [0, \infty) \to [-1, 1], \quad f(x) = \begin{cases} \sin\left(1/x\right) , & x > 0 \\ 0, & x = 0 \end{cases}~ $$ 这个函数在 $x = 0$ 处不连续,因为 $\lim_{x \to 0} f(x)$ 并不存在;但它仍然具有介值性质。另一个更复杂的例子是康威的 13 进制函数。
事实上,达布定理指出:所有某个函数在某区间上的导函数,都具有介值性质——即便它们不一定连续。
从历史上看,这种介值性质曾被一些数学家提议作为实值函数连续性的定义标准之一 \(^\text{[11]}\);但这一定义最终未被采纳。
7. 推广形式
多维空间
庞加莱–米兰达定理是介值定理从一维区间向二维矩形(更一般地,n 维立方体)的一个推广。
Vrahatis 提出了一种类似的推广方式,从三角形推广到更一般的 n 维单纯形。设 $D_n$ 是一个 n 维单纯形,拥有 $n+1$ 个顶点,记作 $v_0, v_1, \dots, v_n$。令 $F = (f_1, f_2, \dots, f_n)$ 是一个从 $D_n$ 到 $\mathbf{R}^n$ 的连续函数,并且在 $D_n$ 的边界上永远不取零值。假设 $F$ 满足以下条件:
- 对于所有 $i \in \{1, \dots, n\}$,函数 $f_i(v_i)$ 的符号与 $f_i(x)$ 在与顶点 $v_i$ 相对的那一面上的所有点 $x$ 的符号相反;
- 向量 $(f_1, \dots, f_n)$ 在顶点 $v_0$ 处的符号向量不同于它在与 $v_0$ 相对的那一面上所有点的符号向量。
那么,存在某个点 $z$ 位于 $D_n$ 的内部,使得:$F(z) = (0, 0, \dots, 0)$
可以通过对 $f_i$ 做标准化,使得每个 $f_i(v_i) > 0$,从而使条件变得更简单:
- 对于所有 $i \in \{1, \dots, n\}$,有 $f_i(v_i) > 0$,并且 $f_i(x) < 0$ 对所有位于与 $v_i$ 相对那一面的点 $x$ 成立。特别地,有 $f_i(v_0) < 0$。
- 对所有在与 $v_0$ 相对的面上的点 $x$,至少存在一个 $i \in \{1, \dots, n\}$ 使得 $f_i(x) > 0$。
该定理可以通过 Knaster–Kuratowski–Mazurkiewicz 引理 来证明,常被用于不动点和零点的数值近似计算 \(^\text{[13]}\)。
一般度量空间与拓扑空间中的情形
介值定理与 “连通性” 的拓扑概念密切相关,并且它可以从度量空间中连通集合的基本性质推导出来,尤其是在实数集 $\mathbb{R}$ 的情形中:
- 如果 $X$ 和 $Y$ 是度量空间,$f: X \to Y$ 是一个连续映射,且 $E \subset X$ 是一个连通子集,那么映像 $f(E)$ 也是连通的。 (*)
- 子集 $E \subset \mathbb{R}$ 是连通的,当且仅当它满足以下性质: 若 $x, y \in E$,且 $x < r < y$,则必有 $r \in E$。 (**)
实际上,连通性是一个拓扑性质,因此性质 (*) 可以推广到一般的拓扑空间中: 如果 $X$ 和 $Y$ 是拓扑空间,$f: X \to Y$ 是连续映射,且 $X$ 是连通空间,则映像 $f(X)$ 仍然是连通的。换句话说,连续映射保持连通性,这一点可以看作是介值定理的一个推广:介值定理是关于实变量实值函数的一个性质,而这里推广到了更一般空间中的连续函数。
回顾我们之前陈述的介值定理第一种形式:
介值定理(版本一)——设 $I = [a, b]$ 是实数集合 $\mathbb{R}$ 中的一个闭区间,且 $f: I \to \mathbb{R}$ 是一个连续函数。那么,若存在一个实数 $u$,满足: $$ \min(f(a), f(b)) < u < \max(f(a), f(b))~ $$ 则存在某个 $c \in (a, b)$,使得:$f(c) = u$ 这就是实数上的介值定理,它也可以看作是连通性在一维实数空间上的具体体现。
介值定理是连通性这两个性质的直接推论:\(^\text{[14]}\);
证明
根据性质(**),区间 $I = [a, b]$ 是一个连通集合。根据性质(*),函数的像集 $f(I)$ 也是连通的。为方便起见,假设 $f(a) < f(b)$。那么再次利用性质(**),如果 $f(a) < u < f(b)$,则可得:$u \in f(I)$ 也就是说,存在某个 $c \in I$ 使得:$f(c) = u$ 由于 $u \ne f(a), f(b)$,因此实际上 $c \in (a, b)$ 必须成立,所需的结论由此得出。如果 $f(b) < f(a)$,则同样的推理也适用,因此我们完成了证明。证毕(Q.E.D.)
推广形式
介值定理可以自然地推广如下:
设 $X$ 是一个连通的拓扑空间,$(Y, <)$ 是一个带有序拓扑的全序集合。令 $f: X \to Y$ 是一个连续映射。若 $a, b \in X$,且 $u \in Y$ 是位于 $f(a)$ 与 $f(b)$ 之间的某个值(按照序关系 <),那么必存在某个 $c \in X$ 使得:$f(c) = u$ 原始的介值定理就是这种推广的一个特例,因为实数集 $\mathbb{R}$ 是连通的,其自然拓扑正是序拓扑。
注:布劳威尔不动点定理是一个相关定理,在一维情况下,它可以视为介值定理的一个特例。
8. 在构造性数学中的情况
- 在构造性数学中,介值定理并不成立。取而代之的是一个削弱版本的结论:我们只能得知该值存在于某个可以任意小的区间内,而不是必然存在某个精确点。设 $a$ 和 $b$ 是两个实数,函数 $f: [a, b] \to \mathbb{R}$ 是从闭区间 $[a, b]$ 到实数轴上的一个**逐点连续函数,并且满足:$f(a) < 0,\quad 0 < f(b)$。那么对于任意正数 $\varepsilon > 0$,总存在某个点 $x \in [a, b]$,使得:$|f(x)| < \varepsilon$。换句话说,虽然我们无法构造出一个确切的零点 $f(x) = 0$,但我们能找到一个点,其函数值可以任意接近 0\(^\text{[15]}\);
9. 实际应用
一个类似的结果是博苏克–乌拉姆定理,它指出:从 $n$-维球面到欧几里得 $n$-维空间的任意连续映射,总存在一对对跖点映射到了同一点。
一维情形的证明
设 $f$ 是一个定义在圆周上的连续函数。我们画一条穿过圆心的直线,与圆交于两对跖点 $A$ 和 $B$。令:$d = f(A) - f(B)$。若将直线旋转 180 度,则 $A$ 和 $B$ 会互换,因此 $d$ 的值会变为 $-d$。由于 $f$ 连续,根据介值定理,在旋转的过程中,必定存在一个中间角度使得 $d = 0$,即:$f(A) = f(B)$ 在这个角度成立。
更一般地说,设一个连续函数定义在某个闭合的凸 $n$-维形状上,对于该形状中任意一个点(不一定是中心),总存在一对以该点为中心的对跖点,其函数值相等。
该定理也为 “转动一个晃动的桌子总能让它稳定下来” 这一现象提供了数学基础(当然是在满足某些容易满足的约束条件下)\(^\text{[16]}\)。
10. 参见
- 平均值定理
- 非原子测度
- 毛球定理
- 斯佩尔纳引理
11. 参考文献
- Weisstein, Eric W. “Bolzano’s Theorem”. MathWorld.
- Cates, Dennis M. (2019). *Cauchy's Calcul Infinitésimal*. 第 249 页. doi:10.1007/978-3-030-11036-9. ISBN 978-3-030-11035-2. S2CID 132587955.
- 基本上遵循 Clarke, Douglas A. (1971). Foundations of Analysis. Appleton-Century-Crofts. 第 284 页.
- 稍作修改的版本见 Abbot, Stephen (2015). Understanding Analysis. Springer. 第 123 页.
- Sanders, Sam (2017). “Nonstandard Analysis and Constructivism!”. arXiv:1704.00281 [math.LO].
- Bos, Henk J. M. (2001). “1590 年前几何程序的合法化”. 收录于 Redefining Geometrical Exactness: Descartes' Transformation of the Early Modern Concept of Construction, Sources and Studies in the History of Mathematics and Physical Sciences. New York: Springer. 第 23–36 页. doi:10.1007/978-1-4613-0087-8_2. ISBN 978-1-4612-6521-4. MR 1800805.
- Russ, S. B. (1980). “Bolzano 关于中值定理论文的翻译”. *Historia Mathematica*. 7 (2): 156–185. doi:10.1016/0315-0860(80)90036-1.
- Grabiner, Judith V. (1983 年 3 月). “Who Gave You the Epsilon? Cauchy and the Origins of Rigorous Calculus” (PDF). The American Mathematical Monthly. 90 (3): 185–194. doi:10.2307/2975545. JSTOR 2975545.
- Karin Usadi Katz 和 Mikhail G. Katz (2011). “A Burgessian Critique of Nominalistic Tendencies in Contemporary Mathematics and its Historiography”. Foundations of Science. doi:10.1007/s10699-011-9223-1.
- O'Connor, John J.; Robertson, Edmund F., “Louis François Antoine Arbogast”, MacTutor History of Mathematics Archive, 圣安德鲁斯大学.
- Smorynski, Craig (2017-04-07). MVT: A Most Valuable Theorem. Springer. ISBN 9783319529561.
- Vrahatis, Michael N. (2016-04-01). “Generalization of the Bolzano theorem for simplices”. Topology and Its Applications. 202: 40–46. doi:10.1016/j.topol.2015.12.066. ISSN 0166-8641.
- Vrahatis, Michael N. (2020-04-15). “Intermediate value theorem for simplices for simplicial approximation of fixed points and zeros”. Topology and Its Applications. 275: 107036. doi:10.1016/j.topol.2019.107036. ISSN 0166-8641.
- Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. 第 42、93 页. ISBN 978-0-07-054235-8.
- Matthew Frank (2020 年 7 月 14 日). “Interpolating Between Choices for the Approximate Intermediate Value Theorem”. Logical Methods in Computer Science. 16 (3). arXiv:1701.02227. doi:10.23638/LMCS-16(3:5)2020.
- Keith Devlin (2007). How to stabilize a wobbly table.
12. 延伸阅读
- [Approximate Intermediate Value Theorem in Pure Constructive Mathematics(在纯构造数学中的近似中值定理)](https://mathoverflow.net/questions/253059/approximate-intermediate-value-theorem-in-pure-constructive-mathematics)
13. 外部链接
- [中值定理 - 波尔查诺定理(cut-the-knot 网站)](https://www.cut-the-knot.org/do_you_know/ivp.shtml)
- [Bolzano's Theorem by Julio Cesar de la Yncera(Wolfram 演示项目)](https://demonstrations.wolfram.com/BolzanosTheorem/)
- [Weisstein, Eric W. “Intermediate Value Theorem” - MathWorld](https://mathworld.wolfram.com/IntermediateValueTheorem.html)
- [Belk, Jim. “Two-dimensional version of the Intermediate Value Theorem”(二维中值定理)- Stack Exchange, 2012 年 1 月 2 日](https://math.stackexchange.com/questions/92612)
- [Mizar 系统中的中值定理证明](http://mizar.org/version/current/html/topreal5.html#T4)
友情链接: 超理论坛 | ©小时科技 保留一切权利