镜面反射（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 镜面反射或规律反射是波（例如光）从表面反射的类似镜面反射的现象。[1]

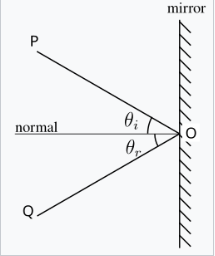
　　 反射定律指出，反射光线从反射表面射出时，与表面法线的夹角与入射光线的夹角相同，但位于表面法线的对侧，且在由入射光线和反射光线构成的平面内。这一行为最早由亚历山大的赫罗（公元约 10 年–70 年）描述。[2] 后来，阿尔哈森给出了反射定律的完整表述。[3][4][5] 他首次指出，入射光线、反射光线和表面的法线都位于一个垂直于反射面平面的同一平面内。[6][7]

　　 镜面反射可以与漫反射进行对比，后者是光从表面散射到多个方向的现象。

1. 反射定律

　　 当光遇到材料的边界时，它会受到该材料对电磁波的光学和电子响应函数的影响。光学过程，包括反射和折射，通常由边界两侧折射率的差异来表达，而反射率和吸收率则是由于材料的电子结构而产生的响应的实部和虚部。[8] 这些过程在传输中的参与程度是光的频率或波长、其偏振状态以及入射角的函数。一般而言，反射随着入射角的增加而增加，并且随着边界吸收率的增加而增强。菲涅尔方程描述了光学边界的物理过程。

　　 反射可以是镜面反射（或镜面式反射）和漫反射。镜面反射将所有从给定方向到达的光反射回相同的角度，而漫反射则将光反射到广泛的方向。这个区别可以通过涂有光泽漆和哑光漆的表面来说明。哑光漆几乎完全表现出漫反射行为，而光泽漆则表现出较大比例的镜面反射行为。由非吸收性粉末（如石膏）构成的表面几乎可以作为完美的漫反射体，而抛光的金属物体则能够非常有效地进行镜面反射。镜子的反射材料通常是铝或银。

　　 光在空间中传播时，表现为电磁场的波前。光线的方向由波前法线（波法线）决定。当光线遇到表面时，波法线与表面法线之间的夹角称为入射角，两个方向所定义的平面为入射平面。入射光线的反射也发生在入射平面内。

　　 反射定律指出，光线的反射角等于入射角，且入射方向、表面法线和反射方向共面。

　　 当光垂直入射到表面时，它会沿源方向直接反射回来。

　　 反射现象源自平面波在平坦边界上的衍射。当边界的尺寸远大于波长时，边界处的电磁场仅在镜面方向上完全同相振荡。

向量形式

　　 反射定律也可以通过线性代数等效地表达。反射光线的方向由入射向量和表面法线向量决定。给定从光源到表面的入射方向 \(\mathbf {\hat {d}}_{\mathrm {i}}\) 和表面法线方向 \(\mathbf {\hat {d}}_{\mathrm {n}}\)，镜面反射方向 \(\mathbf {\hat {d}}_{\mathrm {s}}\)（所有单位向量）为：[9][10] \[ \mathbf {\hat {d}}_{\mathrm {s}} = \mathbf {\hat {d}}_{\mathrm {i}} - 2 \mathbf {\hat {d}}_{\mathrm {n}} \left( \mathbf {\hat {d}}_{\mathrm {n}} \cdot \mathbf {\hat {d}}_{\mathrm {i}} \right)~ \] 其中，\(\mathbf {\hat {d}}_{\mathrm {n}} \cdot \mathbf {\hat {d}}_{\mathrm {i}}\) 是通过点积得到的标量。不同的作者可能会用不同的符号来定义入射方向和反射方向。假设这些欧几里得向量以列向量的形式表示，方程可以等效地表达为矩阵-向量乘法形式：[11] \[ \mathbf {\hat {d}}_{\mathrm {s}} = \mathbf {R} \; \mathbf {\hat {d}}_{\mathrm {i}}~ \] 其中，\(\mathbf {R}\) 是所谓的霍斯特变换矩阵，定义为： \[ \mathbf {R} = \mathbf {I} - 2 \mathbf {\hat {d}}_{\mathrm {n}} \mathbf {\hat {d}}_{\mathrm {n}}^{\mathrm {T}}~ \] 其中 \(\mathbf {I}\) 是单位矩阵，\(\mathbf {\hat {d}}_{\mathrm {n}} \mathbf {\hat {d}}_{\mathrm {n}}^{\mathrm {T}}\) 是法线向量的外积。

2. 反射率

　　 反射率是反射波的功率与入射波功率的比值。它是辐射波长的函数，并且与材料的折射率相关，正如弗涅尔方程所表达的那样。[12] 在材料吸收显著的电磁谱区域，反射率通过复折射率的虚部与电子吸收谱相关联。对于不透明材料，其电子吸收谱很难或不可能直接测量，因此可以通过克拉默斯-克罗尼希变换从反射谱间接确定。反射光的偏振依赖于入射探测光与材料中吸收跃迁偶极矩的排列对称性。

　　 镜面反射的测量使用常规或变入射角反射分光光度计（反射计），并配合扫描变波长光源进行。较低质量的测量可以使用光泽度计，它通过光泽单位量化表面的光泽外观。

3. 后果

内部反射

　　 当光在一种材料中传播并与折射率较低的材料接触时，一部分光会被反射。如果入射角大于临界角，就会发生全内反射：所有的光都会被反射回来。临界角可以表示为： \[ \theta_{\text{crit}} = \arcsin \left(\frac{n_2}{n_1}\right)~ \]

偏振

　　 当光线撞击两个材料的界面时，反射光通常会部分偏振。然而，如果光线在布鲁斯特角处撞击界面，则反射光会完全线性偏振，并且偏振方向平行于界面。布鲁斯特角给出为： \[ \theta_{\mathrm{B}} = \arctan \left(\frac{n_2}{n_1}\right)~ \]

反射图像

　　 参见：镜像 § 三维中的镜像

　　 平面镜中的图像具有以下特征：

• 它距离镜子与物体前方的距离相同。
• 它与物体的大小相同。
• 它是正立的（竖直的）。
• 它是反转的。
• 它是虚像，意味着图像看起来位于镜子后面，无法投影到屏幕上。

　　 平面镜图像的反转在不同情况下的感知方式不同。在许多情况下，镜中的图像看起来像是从左到右反转。如果平面镜安装在天花板上，当一个人站在镜子下并抬头看时，图像可能看起来是上下反转的。类似地，一辆车向左转时，前面车的后视镜中的图像仍然看起来是左转。反转方向与否取决于如何定义方向。更具体地说，镜子改变了坐标系的手性，坐标系的一个轴会出现反转，并且图像的手性可能会改变。例如，右鞋的图像会看起来像左鞋。

4. 例子

　　 除了可见光，镜面反射还可以在电离层的无线电波反射以及飞行物体反射的无线电或微波雷达信号中观察到。X 射线反射率测量技术利用镜面反射率来研究薄膜和界面，具有亚纳米分辨率，使用现代实验室源或同步辐射 X 射线。

　　 非电磁波也可以表现出镜面反射，比如反射声音的声学镜子，以及反射中性原子的原子镜子。为了高效地从固态镜面反射原子，需要使用非常冷的原子和/或小角度入射，以提供显著的量子反射；使用带状镜子来增强原子的镜面反射。中子反射法利用镜面反射来研究材料表面和薄膜界面，这与 X 射线反射法相似。

5. 参见

• 几何光学
• 哈密顿光学
• 反射系数
• 反射（数学）
• 镜面高光
• 镜面性

6. 注释

1. Tan, R.T. (2013), Ikeuchi, Katsushi (编),《镜面反射，镜面反射率》，见：Ikeuchi K.（编），《计算机视觉》（PDF），Springer，波士顿，MA，doi:10.1007/978-0-387-31439-6，ISBN 978-0-387-31439-6，S2CID 5058976
2. Sir Thomas Little Heath (1981)，《希腊数学史》，第二卷：从阿里斯塔克斯到丢番图，ISBN 978-0-486-24074-9。
3. Stamnes, J. J. (2017-11-13)，《焦点区域中的波：光、声和水波的传播、衍射与聚焦》，Routledge，ISBN 978-1-351-40468-6。
4. Mach, Ernst (2013-01-23)，《物理光学原理：历史与哲学的探讨》，Courier Corporation，ISBN 978-0-486-17347-4。
5. Iizuka, Keigo (2013-11-11)，《工程光学》，Springer Science & Business Media，ISBN 978-3-662-07032-1。
6. Selin 2008，第 1817 页。
7. Mach, Ernst (2013-01-23)，《物理光学原理：历史与哲学的探讨》，Courier Corporation，ISBN 978-0-486-17347-4。
8. Fox, Mark (2010)，《固体的光学性质》（第 2 版），牛津大学出版社，第 1 页，ISBN 978-0-19-957336-3。
9. Haines, Eric (2021)，《第 8 章：反射与折射公式》，见 Marrs, Adam；Shirley, Peter；Wald, Ingo（编），《光线追踪宝石 II》，Apress，第 105-108 页，doi:10.1007/978-1-4842-7185-8_8，ISBN 978-1-4842-7185-8，S2CID 238899623。
10. Comninos, Peter (2006)，《计算机图形学的数学与计算机编程技术》，Springer，第 361 页，ISBN 978-1-85233-902-9，存档于 2018-01-14。
11. Farin, Gerald；Hansford, Dianne (2005)，《实用线性代数：几何工具箱》，A K Peters，第 191-192 页，ISBN 978-1-56881-234-2，存档于 2010-03-07。实用线性代数：几何工具箱（Google Books）
12. Hecht 1987，第 100 页。

7. 参考文献

• Hecht, Eugene (1987)，《光学》（第 2 版），Addison Wesley，ISBN 0-201-11609-X。