集合（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学中，集合是不同事物的集合；这些事物被称为集合的元素或成员，通常是任何类型的数学对象：数字、符号、空间中的点、线条、其他几何形状、变量，甚至是其他集合。集合可以是有限的或无限的，具体取决于其元素的数量是否有限。存在一个没有元素的唯一集合，称为空集；只有一个元素的集合称为单集合。

　　 集合在现代数学中无处不在。实际上，集合理论，特别是泽尔梅洛-弗兰克尔集合理论，自 20 世纪上半叶以来，已经成为为所有数学分支提供严谨基础的标准方法。

1. 背景

　　 在 19 世纪末之前，集合并没有被专门研究，也没有与数列明确区分开来。大多数数学家认为无穷大是潜在的——意味着它是一个无尽过程的结果——因此他们不愿意考虑无限集合，即那些成员数量不是自然数的集合。具体来说，一条线并没有被看作是其点的集合，而是看作一个点可能位于其中的轨迹。

　　 无限集合的数学研究始于乔治·康托尔（Georg Cantor，1845-1918）。这带来了一些违反直觉的事实和悖论。例如，数轴上有一个无限多个元素，其数量严格大于自然数的无限集合，而任何线段的元素数量与整个空间相同。此外，拉塞尔悖论意味着 “所有集合的集合” 这一短语是自我矛盾的。

　　 这些违反直觉的结果，加上其他的悖论，导致了数学的基础危机，最终通过广泛采纳泽尔梅洛-弗兰克尔集合理论作为集合论和所有数学的坚实基础得以解决。

　　 与此同时，集合开始在所有数学领域广泛应用。特别是，代数结构和数学空间通常是通过集合来定义的。此外，许多较早的数学成果也以集合的形式重新表述。例如，欧几里得的定理常常被表述为 “素数集合是无限的”。大卫·希尔伯特曾预言，集合在数学中的广泛使用：“没有人会把我们从康托尔为我们创造的天堂中赶出去。”

　　 通常，数学中对集合的常见使用并不需要泽尔梅洛-弗兰克尔集合理论的完整能力。在数学实践中，集合可以独立于该理论的逻辑框架进行操作。

　　 本文的目的是总结在数学中常用的集合操作规则和属性，而不涉及任何逻辑框架。对于研究集合的数学分支，请参见集合论；对于对应逻辑框架的非正式介绍，请参见朴素集合论；对于更正式的介绍，请参见公理化集合论和泽尔梅洛-弗兰克尔集合理论。

2. 基本概念

　　 在数学中，集合是不同事物的集合。这些事物被称为集合的元素或成员，通常是任何类型的数学对象，如数字、符号、空间中的点、线条、其他几何形状、变量、函数，甚至是其他集合。集合有时也被称为集合或族，特别是当其元素本身是集合时；这样可以避免集合与其成员之间的混淆，并使阅读更加清晰。集合可以通过列出其元素或通过一个描述其元素的性质来指定，例如素数集合或某一班级所有学生的集合。

　　 如果 \( x \) 是集合 \( S \) 的元素，则称 \( x \) 属于 \( S \) 或 \( x \) 在 \( S \) 中，表示为 \( x \in S \)。声明 " \( y \) 不在 \( S \) 中" 表示为 \( y \notin S \)，也可以读作 " \( y \) 不在 \( S \) 中"。例如，如果 \( \mathbb{Z} \) 是整数的集合，那么 \( -3 \in \mathbb{Z} \) 和 \( 1.5 \notin \mathbb{Z} \)。

　　 每个集合通过其元素唯一地定义。特别地，两个集合如果具有完全相同的元素，它们是相等的（它们是相同的集合）。这个性质叫做外延性，可以用公式写为： \[ A = B \iff \forall x\; (x \in A \iff x \in B)~ \] 这意味着只有一个没有元素的集合，称为空集（或零集），表示为 \( \varnothing \) 或 \( \emptyset \)，或者 \( \{\} \)。单集合是一个只有一个元素的集合。如果 \( x \) 是这个元素，则单集合表示为 \( \{x\} \)。如果 \( x \) 本身是一个集合，它不能与 \( \{x\} \) 混淆。例如，\( \emptyset \) 是一个没有元素的集合，而 \( \{\emptyset\} \) 是一个以 \( \emptyset \) 为唯一元素的单集合。

　　 如果存在一个自然数 \( n \)，使得前 \( n \) 个自然数可以与集合的元素一一对应，则该集合是有限的。在这种情况下，称 \( n \) 为集合的元素个数。如果不存在这样的 \( n \)，则集合是无限的。空集是一个有限集合，具有 \( 0 \) 个元素。

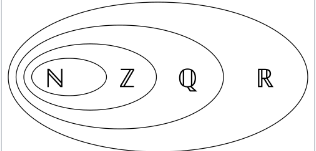
　　 自然数构成一个无限集合，通常表示为 \( \mathbb{N} \)。其他无限集合的例子包括包含自然数的数集、实数向量空间、曲线和大多数类型的空间。

3. 指定一个集合

　　 外延性意味着，在指定一个集合时，必须么列出其元素，要么提供一个唯一描述集合元素的性质。

列举法符号

　　 列举法符号是由恩斯特·泽尔梅洛于 1908 年引入的符号，通过在花括号内列出集合的元素并用逗号分隔来指定一个集合。例如，集合 \( \{4, 2, 1, 3\} \) 和 \( \{\text{blue, white, red}\} \) 表示的是集合而不是元组，因为它们被花括号包围。

　　 上面的符号 \( \{\} \) 和 \( \{x\} \) 分别表示空集和单集合，这些都是列举法符号的例子。

　　 在指定集合时，唯一重要的是每个不同的元素是否属于该集合；这意味着如果元素重复或顺序改变，集合本身不会发生变化。例如： \[ \{1, 2, 3, 4\} = \{4, 2, 1, 3\} = \{4, 2, 4, 3, 1, 3\}~ \] 当存在明确的生成所有集合元素的模式时，可以使用省略号来简化符号，如表示不大于 1000 的正整数集合： \[ \{1, 2, 3, \ldots, 1000\}~ \] 省略号也可以用来扩展列举法符号，表示一些无限集合。例如，所有整数的集合可以表示为： \[ \{\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots\}~ \] 或者： \[ \{0, 1, -1, 2, -2, 3, -3, \ldots\}~ \]

集合描述符号

　　 集合描述符号通过指定满足某些逻辑公式的所有元素来定义一个集合。更精确地说，如果 \( P(x) \) 是一个依赖于变量 \( x \) 的逻辑公式，该公式根据 \( x \) 的值评估为真或假，那么： \[ \{x \mid P(x)\} \quad \text{或} \quad \{x : P(x)\}~ \] 表示所有使得 \( P(x) \) 为真的 \( x \) 的集合。例如，可以如下指定集合 \( F \)： \[ F = \{n \mid n \text{ 是整数，且 } 0 \leq n \leq 19\}~ \] 在这种符号中，竖线符号 "|" 读作 "使得"，整个公式可以读作 "\(F\) 是所有 \( n \) 的集合，使得 \( n \) 是一个在 0 到 19 范围内的整数"。

　　 某些逻辑公式，如 \( S \) 是一个集合 或 \( S \) 是一个集合且 \( S \notin S \)，不能用于集合描述符号，因为没有一个集合的元素能够由该公式来描述。为了解决这个问题，可以采取几种方法。可以证明公式定义了一个集合；这通常是显而易见的，但也可能非常困难。

　　 还可以引入一个更大的集合 \( U \)，它必须包含指定集合的所有元素，并将符号写作： \[ \{x \mid x \in U \text{ 且 ...}\} \quad \text{或} \quad \{x \in U \mid \text{ ...}\}~ \] 也可以事先定义 \( U \)，并约定每个出现在符号竖线左边的变量代表 \( U \) 的元素。这意味着在集合描述符号中 \( x \in U \) 是隐含的。在这种情况下，\( U \) 通常被称为讨论域或宇宙。

　　 例如，假设小写拉丁字母表示一个实数且仅此而已，则表达式 \[ \{x \mid x \notin \mathbb{Q}\}~ \] 是 \[ \{x \in \mathbb{R} \mid x \notin \mathbb{Q}\}~ \] 的简写，定义了无理数集合。

4. 子集

　　 集合 \( B \) 的子集是一个集合 \( A \)，使得 \( A \) 的每个元素也是 \( B \) 的元素。如果 \( A \) 是 \( B \) 的子集，通常说 \( A \) 包含于 \( B \)，\( B \) 包含 \( A \)，或 \( B \) 是 \( A \) 的超集。这表示为 \( A \subseteq B \) 和 \( B \supseteq A \)。然而，许多作者使用 \( A \subset B \) 和 \( B \supset A \) 来表示。子集的定义可以用符号表示为： \[ A \subseteq B \quad \text{当且仅当} \quad \forall x \; (x \in A \implies x \in B)~ \] 如果集合 \( A \) 是集合 \( B \) 的子集并且 \( A \neq B \)，则称 \( A \) 是 \( B \) 的真子集。这表示为 \( A \subset B \) 和 \( B \supset A \)。当使用 \( A \subset B \) 表示子集关系时，或者在可能产生歧义的情况下，通常使用 \( A \subsetneq B \) 和 \( B \supsetneq A \)。

　　 通过符号 \( \subseteq \) 建立的集合之间的关系称为包含关系或包含性。集合之间的相等可以通过子集来表达。两个集合当且仅当它们彼此包含时才相等：即 \( A \subseteq B \) 和 \( B \subseteq A \) 等价于 \( A = B \)。空集是每个集合的子集：\( \emptyset \subseteq A \)。

　　 示例：

• 所有人的集合是所有哺乳动物集合的真子集。
• \( \{1, 3\} \subset \{1, 2, 3, 4\} \)
• \( \{1, 2, 3, 4\} \subseteq \{1, 2, 3, 4\} \)

5. 基本操作

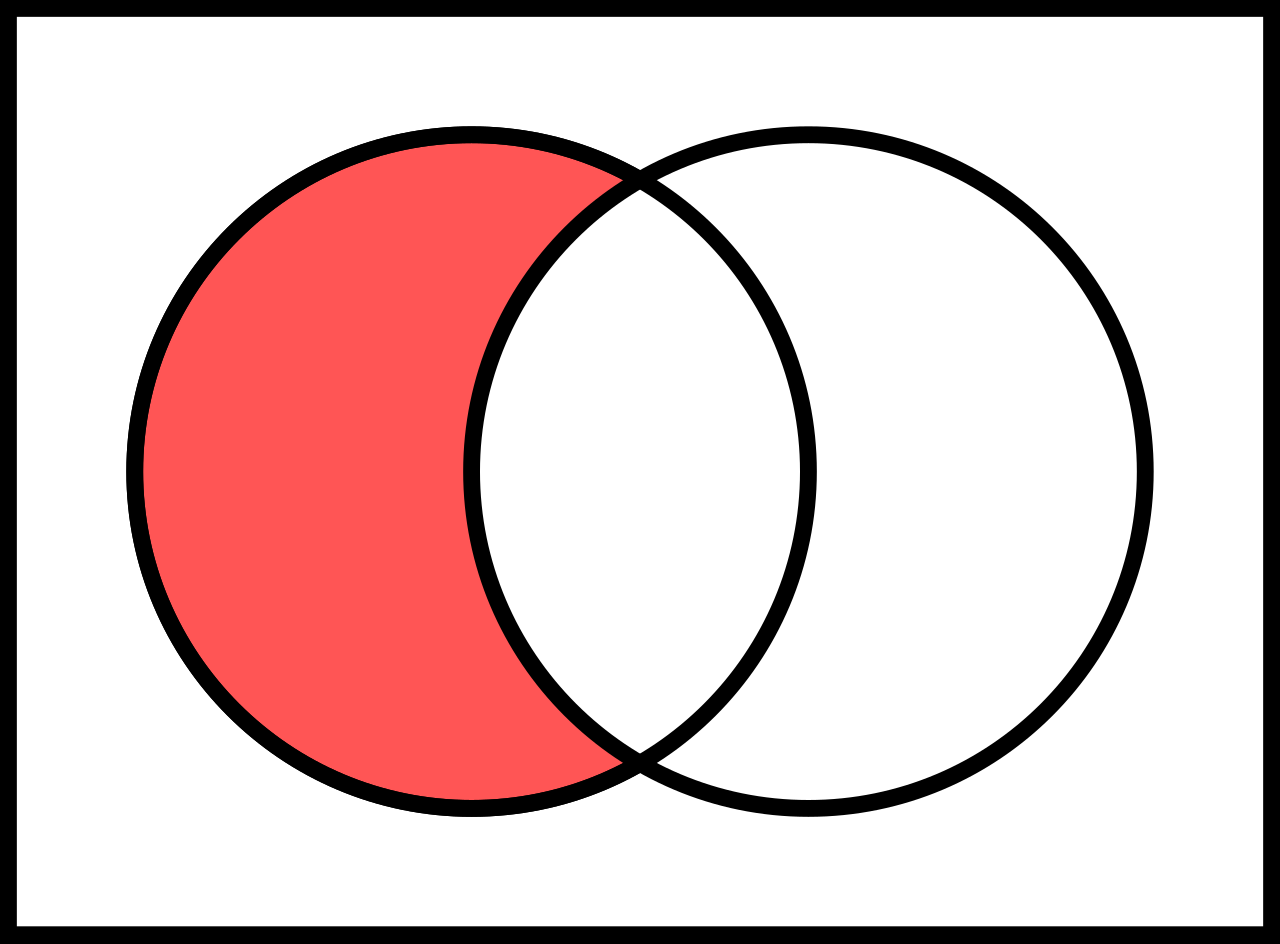
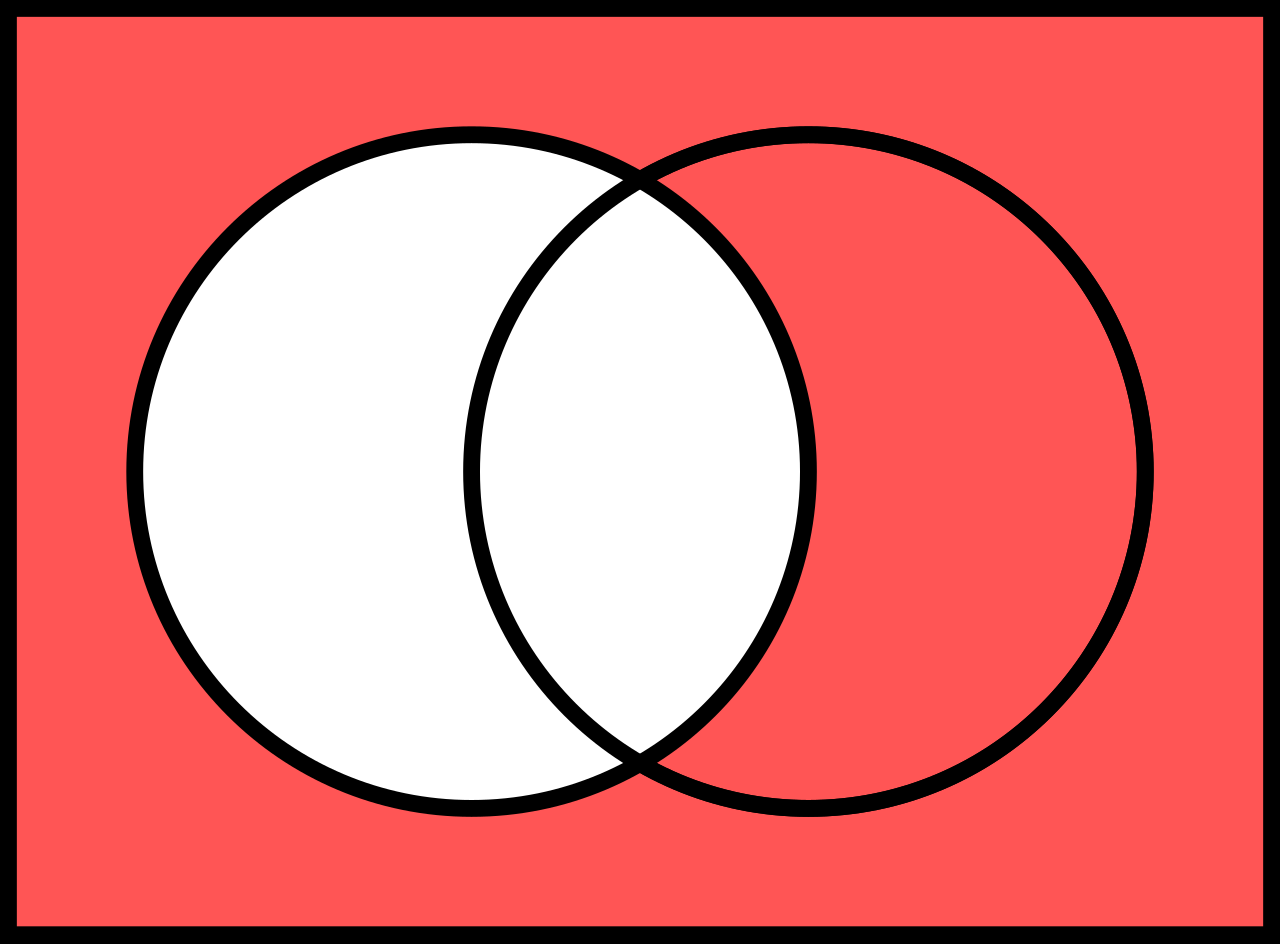
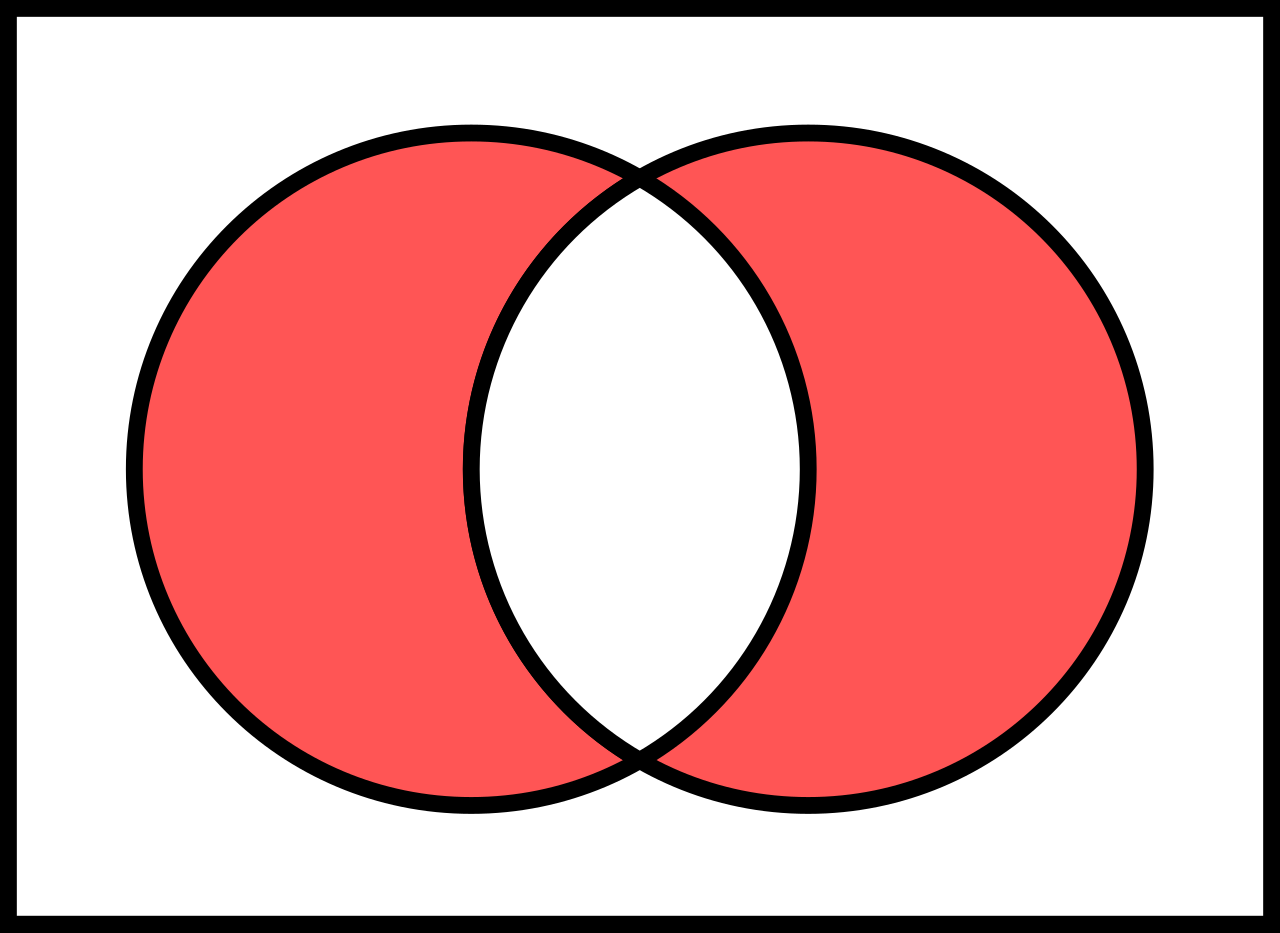
　　 有几个标准操作可以从给定的集合中生成新的集合，类似于加法和乘法可以从给定的数字中生成新的数字。本节讨论的操作是那些生成的集合中的所有元素都属于先前定义的集合的操作。这些操作通常通过欧拉图和维恩图来说明。

　　 集合的主要基本操作如下。

交集

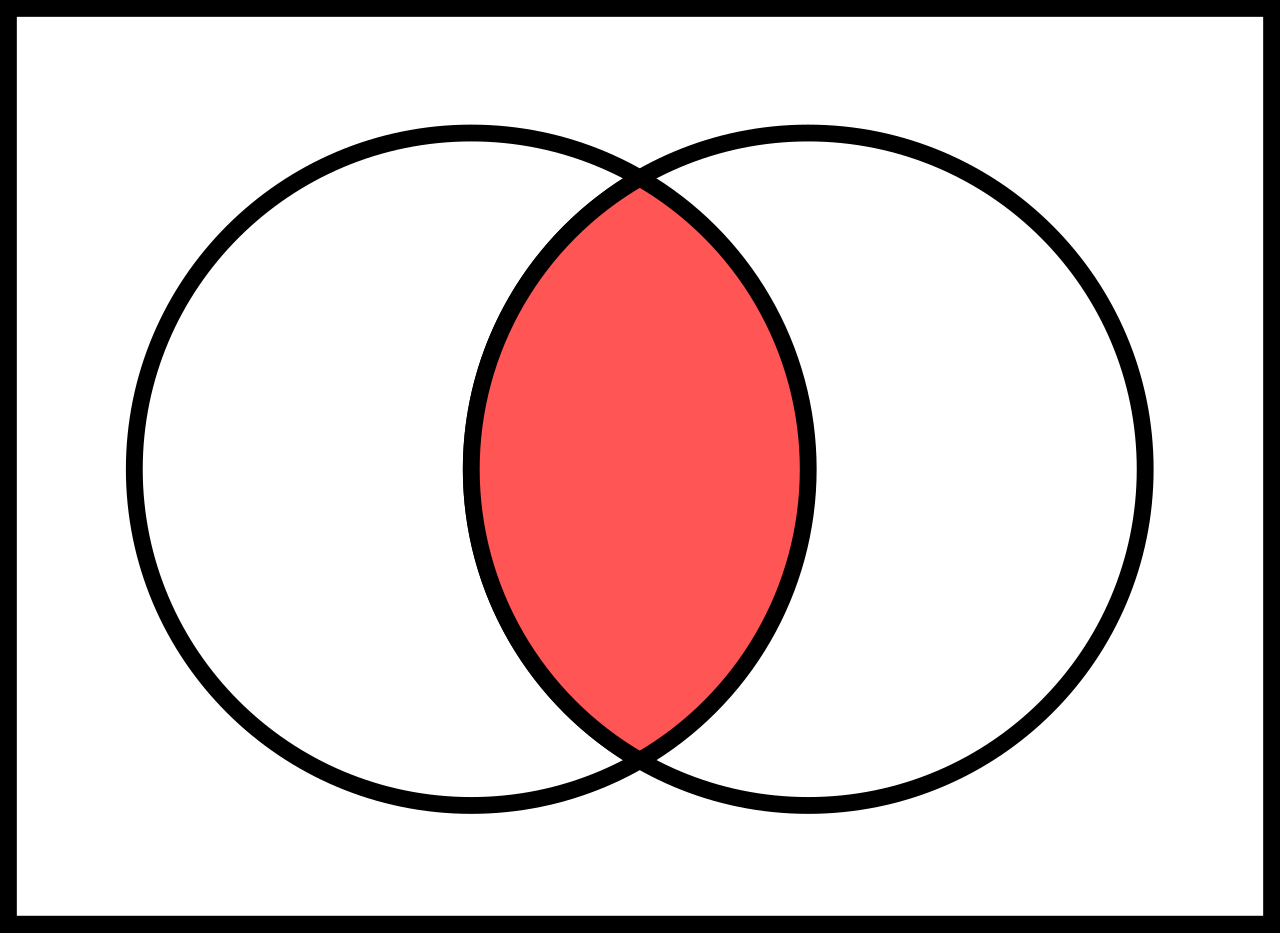
　　 两个集合 \( A \) 和 \( B \) 的交集是一个集合，表示为 \( A \cap B \)，其元素是既属于 \( A \) 又属于 \( B \) 的元素。即： \[ A \cap B = \{x \mid x \in A \land x \in B\}~ \] 其中 \( \land \) 表示逻辑 “与” 运算。

　　 交集是结合律和交换律的；这意味着在进行一系列交集运算时，可以任意顺序进行，无需括号来指定操作顺序。交集没有通用的单位元素。然而，如果将交集限制为给定集合 \( U \) 的子集，那么交集的单位元素是 \( U \)。

　　 如果 \( \mathcal{S} \) 是一个非空的集合族，则其交集，表示为 \( \bigcap_{A \in \mathcal{S}} A \)，是一个集合，其元素是属于 \( \mathcal{S} \) 中所有集合的元素。即： \[ \bigcap_{A \in \mathcal{S}} A = \{x \mid (\forall A \in \mathcal{S})\; x \in A\}~ \] 当 \( \mathcal{S} \) 只有两个元素时，这两个交集的定义是等价的。

并集

　　 两个集合 \( A \) 和 \( B \) 的并集是一个集合，表示为 \( A \cup B \)，其元素是属于 \( A \)、\( B \) 或者两者的元素。即： \[ A \cup B = \{x \mid x \in A \lor x \in B\}~ \] 其中 \( \lor \) 表示逻辑 “或” 运算。

　　 并集是结合律和交换律的；这意味着在进行一系列并集运算时，可以任意顺序进行，无需括号来指定操作顺序。空集是并集运算的单位元素。

　　 如果 \( \mathcal{S} \) 是一个集合族，则其并集，表示为 \( \bigcup_{A \in \mathcal{S}} A \)，是一个集合，其元素是属于 \( \mathcal{S} \) 中至少一个集合的元素。即： \[ \bigcup_{A \in \mathcal{S}} A = \{x \mid (\exists A \in \mathcal{S})\; x \in A\}~ \] 当 \( \mathcal{S} \) 只有两个元素时，这两个并集的定义是等价的。

集合差

　　 两个集合 \( A \) 和 \( B \) 的集合差是一个集合，表示为 \( A \setminus B \) 或 \( A - B \)，其元素是属于 \( A \) 但不属于 \( B \) 的元素。即： \[ A \setminus B = \{x \mid x \in A \land x \notin B\}~ \] 其中 \( \land \) 表示逻辑 “与” 运算。

　　 当 \( B \subseteq A \) 时，差集 \( A \setminus B \) 也称为 \( B \) 在 \( A \) 中的补集。当所有考虑的集合都是固定的全集 \( U \) 的子集时，补集 \( U \setminus A \) 通常称为 \( A \) 的绝对补集。

　　 两个集合 \( A \) 和 \( B \) 的对称差，表示为 \( A \, \Delta \, B \)，是一个集合，其中的元素属于 \( A \) 或 \( B \) 但不属于两者。即： \[ A \, \Delta \, B = (A \setminus B) \cup (B \setminus A)~ \]

子集代数

　　 集合 \( U \) 的所有子集构成的集合称为 \( U \) 的幂集，通常表示为 \( \mathcal{P}(U) \)。幂集是一个代数结构，其主要运算包括并集、交集、集合差、对称差和绝对补集（即在 \( U \) 中的补集）。

　　 幂集是一个布尔环，其中对称差作为加法，交集作为乘法，空集作为加法单位，\( U \) 作为乘法单位，补集作为加法逆元。

　　 幂集也是一个布尔代数，其中联合（\( \lor \)）是并集（\( \cup \)），交（\( \land \)）是交集（\( \cap \)），而否定是集合补集。

　　 像所有布尔代数一样，幂集也是一个部分有序集合，按照集合包含关系排序。它也是一个完全格。

　　 这些结构的公理引出了许多与子集相关的恒等式，详细内容请参见相关链接文章。

6. 函数

　　 从集合 \( A \)（定义域）到集合 \( B \)（值域）的一个函数是一个规则，它将 \( A \) 中的每个元素映射到 \( B \) 中的一个唯一元素。例如，平方函数将每个实数 \( x \) 映射到 \( x^2 \)。函数可以通过其图像形式在集合中正式定义，图像是定义域和值域的笛卡尔积的子集（见下文）。

　　 函数是集合论的基础，接下来的章节将给出一些示例。

带索引的族

　　 直观地说，带索引的族是一个集合，其元素通过另一个集合（索引集）的元素进行标记。这些标记允许同一个元素在族中多次出现。

　　 正式地，带索引的族是一个函数，其定义域为索引集。通常，带索引的族不使用常规的函数符号 \( f(x) \)。相反，索引集的元素作为族名称的下标写出，例如 \( a_i \)。

　　 当索引集为 \( \{1, 2\} \) 时，带索引的族称为有序对；当索引集为前 \( n \) 个自然数的集合时，带索引的族称为 \( n \)-元组；当索引集为所有自然数的集合时，带索引的族称为序列。

　　 在所有这些情况下，自然数的自然顺序允许省略显式带索引的族中的索引。例如，\( (b, 2, b) \) 表示一个三元组 \( A \)，其中 \( A_1 = b \), \( A_2 = 2 \), \( A_3 = b \)。

　　 上述符号 \( \bigcup_{A \in \mathcal{S}} A \) 和 \( \bigcap_{A \in \mathcal{S}} A \) 通常会被带索引的族符号所替代，即： \[ \bigcup_{i \in \mathcal{I}} A_i = \{x \mid (\exists i \in \mathcal{I}) \; x \in A_i\}~ \] 和 \[ \bigcap_{i \in \mathcal{I}} A_i = \{x \mid (\forall i \in \mathcal{I}) \; x \in A_i\}~ \] 上述公式是带索引的族公式的特例，其中 \( \mathcal{S} = \mathcal{I} \) 且 \( i = A = A_i \)。即使在某些 \( i \neq j \) 时 \( A_i = A_j \)，这些公式仍然正确，因为 \( A = A \cup A = A \cap A \)。

7. 外部操作

　　 在 “基本操作” 部分，通过集合操作产生的所有集合的元素都属于先前定义的集合。在本节中，考虑了其他集合操作，这些操作产生的集合的元素可能超出所有先前考虑的集合。这些操作包括笛卡尔积、非交并集、集合指数运算和幂集。

笛卡尔积

　　 笛卡尔积已经用于定义函数。

　　 给定两个集合 \( A_1 \) 和 \( A_2 \)，它们的笛卡尔积，表示为 \( A_1 \times A_2 \)，是由所有有序对 \( (a_1, a_2) \) 组成的集合，其中 \( a_1 \in A_1 \) 且 \( a_2 \in A_2 \)。即： \[ A_1 \times A_2 = \{(a_1, a_2) \mid a_1 \in A_1 \land a_2 \in A_2\}~ \] 这个定义并不要求这两个集合不同。特别地， \[ A \times A = \{(a_1, a_2) \mid a_1 \in A \land a_2 \in A\}~ \] 由于这个定义涉及一对索引（1, 2），它可以直接推广到任何带索引的集合族的笛卡尔积或直积： \[ \prod_{i \in \mathcal{I}} A_i = \{(a_i)_{i \in \mathcal{I}} \mid (\forall i \in \mathcal{I}) \; a_i \in A_i\}~ \] 即，集合族的笛卡尔积的元素是所有元素的族，使得每个元素属于相同索引的集合。对于每个非空集合族，笛卡尔积是非空集合的事实是由选择公理保证的。

集合指数运算

　　 给定两个集合 \( E \) 和 \( F \)，集合指数运算，表示为 \( F^E \)，是一个集合，其中的元素是从 \( E \) 到 \( F \) 的所有函数。

　　 等价地，\( F^E \) 可以看作是一个由 \( E \) 索引的集合族的笛卡尔积，这些集合都等于 \( F \)。这解释了该术语和符号的来源，因为带有整数指数的指数运算本质上是一个乘积，其中所有因子都等于底数。

幂集

　　 集合 \( E \) 的幂集是一个集合，其中的元素是 \( E \) 的所有子集，包括空集和 \( E \) 本身。它通常表示为 \( \mathcal{P}(E) \)。例如， \[ \mathcal{P}(\{1,2,3\}) = \{\emptyset, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\}\}~ \] 集合 \( E \) 的子集和从 \( E \) 到 \( \{0, 1\} \) 的函数之间存在自然的一一对应（双射）；这种对应关系将每个子集与一个函数关联，该函数在子集上取值为 1，在其他地方取值为 0。由于这种对应关系，\( E \) 的幂集通常被与集合指数运算等同： \[ \mathcal{P}(E) = \{0,1\}^E~ \] 在这种符号中，\( \{0,1\} \) 常常简写为 2，因此： \[ \mathcal{P}(E) = 2^E~ \] 特别地，如果 \( E \) 有 \( n \) 个元素，那么 \( 2^E \) 具有 \( 2^n \) 个元素。

非交并集

　　 两个或更多集合的非交并集类似于并集，但如果两个集合有公共元素，这些元素在非交并集中被视为不同的元素。这是通过用集合的索引标记元素来实现的，标记表示元素来自哪个集合。

　　 两个集合 \( A \) 和 \( B \) 的非交并集通常表示为 \( A \sqcup B \)，定义为： \[ A \sqcup B = \{(a, i) \mid (i = 1 \land a \in A) \lor (i = 2 \land a \in B)\}~ \] 如果 \( A = B \) 是一个包含 \( n \) 个元素的集合，那么 \( A \cup A = A \) 仍然有 \( n \) 个元素，而 \( A \sqcup A \) 则有 \( 2n \) 个元素。

　　 两个集合的非交并集是带索引的集合族的非交并集的特例，定义为： \[ \bigsqcup_{i \in \mathcal{I}} = \{(a, i) \mid i \in \mathcal{I} \land a \in A_i\}~ \] 非交并集是集合范畴中的余积。因此，符号 \[ \coprod_{i \in \mathcal{I}} = \{(a, i) \mid i \in \mathcal{I} \land a \in A_i\}~ \] 通常被使用。

　　 内部非交并集

　　 给定一个带索引的集合族 \( (A_i)_{i \in \mathcal{I}} \)，存在一个自然的映射： \[ \bigsqcup_{i \in \mathcal{I}} A_i \to \bigcup_{i \in \mathcal{I}} A_i \quad (a, i) \mapsto a~ \] 这个映射的作用是 “忘记” 索引。

　　 这个映射总是满射；当且仅当集合 \( A_i \) 两两互不相交时，它是双射，即集合族中任意两个集合的交集为空。在这种情况下，\( \bigcup_{i \in \mathcal{I}} A_i \) 和 \( \bigsqcup_{i \in \mathcal{I}} A_i \) 通常被视为相同，称它们的并集是集合族成员的非交并集。

　　 如果一个集合是某个子集族的非交并集，则也称该子集族是该集合的划分。

8. 基数

　　 非正式地，集合 \( S \) 的基数，通常表示为 \( |S| \)，是其成员的数量。

　　 当考虑的集合与集合 \( \{1, 2, \dots, n\} \)（即前 \( n \) 个自然数的集合）之间存在一一对应时，这个数量就是自然数 \( n \)。空集的基数是 0。在这两种情况下，集合称为有限集合。否则，集合是无限集合。

　　 自然数用于度量有限集合的基数这一事实，是自然数概念的基础，并且在集合概念出现之前已有数千年的历史。组合数学的很大一部分致力于有限集合基数的计算或估计。

无限基数

　　 无限集合的基数通常通过一个基数数来表示，正如有限集合的元素数量通过自然数来表示一样。基数数的定义过于技术性，超出了本文的范围；然而，许多基数的性质可以在不引用基数数的情况下处理，具体如下。

　　 如果两个集合 \( S \) 和 \( T \) 之间存在一一对应（双射），则它们具有相同的基数。这表示为：\(|S| = |T|\) 这将是集合上的等价关系，如果所有集合的集合存在的话。

　　 例如，自然数和偶数自然数具有相同的基数，因为乘以 2 提供了这样一个双射。同样，区间 \( (-1, 1) \) 和所有实数的集合具有相同的基数，双射由函数 \( x \mapsto \tan\left(\pi x / 2\right) \) 提供。

　　 拥有与其真子集相同基数是无限集合的一个特征性质：当且仅当集合的基数与其某个真子集的基数相同时，该集合是无限集合。所以，通过上面的例子，自然数集合是一个无限集合。

　　 除了相等之外，基数之间还有一种自然的不等关系：如果存在从集合 \( S \) 到集合 \( T \) 的单射，则集合 \( S \) 的基数小于或等于集合 \( T \) 的基数。这表示为：\(|S| \leq |T|\)

　　 施罗德–伯恩斯坦定理表明，\( |S| \leq |T| \) 和 \( |T| \leq |S| \) 说明 \( |S| = |T| \)。此外，如果并且仅当存在从 \( T \) 到 \( S \) 的满射时，才有 \( |S| \leq |T| \)。对于每一对集合 \( S \) 和 \( T \)，要么有 \( |S| \leq |T| \)，要么有 \( |T| \leq |S| \)。因此，基数的不等关系是一个全序关系。

　　 自然数集合 \( \mathbb{N} \) 的基数，表示为 \( |\mathbb{N}| = \aleph_0 \)，是最小的无限基数。这意味着，如果 \( S \) 是一个自然数集合，则 \( S \) 要么是有限集合，要么有 \( |S| = |\mathbb{N}| \)。

　　 基数小于或等于 \( |\mathbb{N}| = \aleph_0 \) 的集合称为可数集合；这些集合要么是有限集合，要么是可数无限集合（基数为 \( \aleph_0 \) 的集合）；一些作者使用 “可数” 来表示 “可数无限”。基数严格大于 \( \aleph_0 \) 的集合称为不可数集合。

　　 康托尔的对角线论证表明，对于每个集合 \( S \)，其幂集（即其子集的集合）\( 2^S \) 具有更大的基数： \[ |S| < |2^S|~ \] 这意味着不存在最大的基数。

实数的基数

　　 实数集合的基数称为连续统的基数，表示为 \( \mathfrak{c} \)。（“连续统” 一词在 20 世纪之前指的是实数线，当时实数线并不常常被看作是一个数字集合。）

　　 如上所述，实数线 \( \mathbb{R} \) 与一个开区间具有相同的基数，因此每一个包含非空开区间的 \( \mathbb{R} \) 的子集，其基数也为 \( \mathfrak{c} \)。 有： \[ \mathfrak{c} = 2^{\aleph_0}~ \] 这意味着实数的基数等于自然数的幂集的基数。特别地： \[ \mathfrak{c} > \aleph_0~ \] 当乔治·康托尔于 1878 年发表这一结果时，这一结果令人震惊，甚至遭到数学家的拒绝，经过几十年的时间才被普遍接受。

　　 可以证明，\( \mathfrak{c} \) 也是整个平面以及任何有限维欧几里得空间的基数。

　　 连续统假设是乔治·康托尔于 1878 年提出的猜想，认为没有基数严格介于 \( \aleph_0 \) 和 \( \mathfrak{c} \) 之间的集合。1963 年，保罗·科恩证明了连续统假设与泽尔梅洛–弗兰克尔集合理论（带选择公理）的公理独立。这意味着，如果最广泛使用的集合理论是一致的（即没有自相矛盾），那么无论是加入连续统假设作为一个进一步的公理的集合理论，还是加入连续统假设的否定的集合理论，都是一致的。

9. 选择公理

　　 非正式地，选择公理指出，给定任何一族非空集合，可以同时在每个集合中选择一个元素。以这种方式表述，这个公理的可接受性提出了一个基础的逻辑问题，因为很难想象一个无限的瞬时动作。然而，存在几个等价的表述，这些表述争议较小，并且在许多数学领域有着深远的影响。如今，选择公理在主流数学中通常被接受。

　　 选择公理的更正式的表述是：每个带索引的非空集合族的笛卡尔积是非空的。

　　 其他等价形式将在以下小节中描述。

佐恩引理

　　 佐恩引理是一个与选择公理等价的命题，在集合论的其他公理下，并且在通常的数学中更容易使用。

　　 设 \( S \) 是一个部分有序集合。\( S \) 中的链是一个在诱导的顺序下是全序的子集。佐恩引理指出，如果 \( S \) 中的每个链都有一个上界，那么 \( S \) 至少有一个最大元素，即一个不小于 \( S \) 中其他元素的元素。

　　 在佐恩引理的多数应用中，\( S \) 是一个集合族，顺序是集合包含关系，链的上界被取为其成员的并集。

　　 佐恩引理的一个应用例子是证明每个向量空间都有一个基。在这里，\( S \) 的元素是向量空间的线性无关子集。一个链的元素的并集是线性无关的，因为一个无限集合是线性无关的，当且仅当每个有限子集是线性无关的，而链的并集的每个有限子集都必须包含在链的某个成员中。因此，存在一个最大的线性无关集。由于最大性，这个线性无关集必须张成整个向量空间，因此是该空间的基。

　　 佐恩引理的另一个经典应用是证明每个真理想——即不是整个环的理想——都包含在一个最大理想中。在这里，\( S \) 是包含给定理想的所有真理想的集合。理想的链的并集仍是一个理想，因为理想的公理涉及有限个元素。真理想链的并集是一个真理想，因为否则 1 会属于这个并集，这就意味着它属于链的某个成员。

　　 **超限归纳法**

　　 **主要文章：** 良序 和 超限归纳法

　　 选择公理与每个集合上可以定义一个良序的事实是等价的，其中良序是一个全序，使得每个非空子集都有最小元素。

　　 良序集合的简单例子是自然数（按照自然顺序），以及对于每个 \( n \)，自然数的 \( n \)-元组集合，按字典顺序排列。

　　 良序允许数学归纳法的一种推广，称为超限归纳法。给定一个依赖于自然数的性质（谓词）\( P(n) \)，数学归纳法的事实是，要证明 \( P(n) \) 始终为真，只需要证明对于每个 \( n \)，有： \[ (m < n \implies P(m)) \implies P(n)~ \] 超限归纳法与此相同，只是将自然数替换为良序集合的元素。

　　 通常，如果分别证明三个案例，超限归纳法的证明会更容易，前两个案例与常规归纳法相同：

1. \( P(0) \) 成立，其中 \( 0 \) 表示良序集合的最小元素。
2. \( P(x) \implies P(S(x)) \)，其中 \( S(x) \) 表示 \( x \) 的后继元素，即比 \( x \) 大的最小元素。
3. \( (\forall y; \; y < x \implies P(y)) \implies P(x) \)，当 \( x \) 不是后继元素时。

　　 超限归纳法对于定义序数和基数非常重要。

10. 参见

• 集合代数
• 替代集合论
• 集合的范畴
• 类（集合论）
• 集合族
• 模糊集合
• 部件论
• 数学原理

11. 注释

　　 a.有时会使用一些排版变体，例如 \( \varphi \) [15] 或 \( \phi \) [16]。
b."单集合" 这一术语有时也会被使用 [14]。
c.这个性质等价于选择公理。
d.集合论的一致性不能在其内部证明。
e.Gödel [44] 和 Cohen [45] 分别证明了选择公理不能从剩余的集合论公理中证明或反驳。

12. 引用文献

1. Hilbert, David (1926), "Über das Unendliche", *Mathematische Annalen*, vol. 95, pp. 161–190, doi:10.1007/BF01206605, JFM 51.0044.02, S2CID 121888793 "Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können." 翻译见 Van Heijenoort, Jean, *On the infinite*, Harvard University Press
2. Cantor, Georg; Jourdain, Philip E.B. (Translator) (1915). *Contributions to the founding of the theory of transfinite numbers*. New York Dover Publications (1954 English translation). By an 'aggregate' (Menge) we are to understand any collection into a whole (Zusammenfassung zu einem Ganzen) M of definite and separate objects m of our intuition or our thought. Here: p.85
3. P. K. Jain; Khalil Ahmad; Om P. Ahuja (1995). *Functional Analysis*. New Age International. p. 1. ISBN 978-81-224-0801-0.
4. Samuel Goldberg (1 January 1986). *Probability: An Introduction*. Courier Corporation. p. 2. ISBN 978-0-486-65252-8.
5. Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein (2001). *Introduction To Algorithms*. MIT Press. p. 1070. ISBN 978-0-262-03293-3.
6. Halmos 1960, p. 1.
7. Maddocks, J. R. (2004). Lerner, K. Lee; Lerner, Brenda Wilmoth (eds.). *The Gale Encyclopedia of Science*. Gale. pp. 3587–3589. ISBN 0-7876-7559-8.
8. Devlin, Keith J. (1981). "Sets and functions". *Sets, Functions and Logic: Basic concepts of university mathematics*. Springer. ISBN 978-0-412-22660-1.
9. "Set - Encyclopedia of Mathematics". *encyclopediaofmath.org*. Retrieved 2025-02-06.
10. Publishers, HarperCollins. "The American Heritage Dictionary entry: set". *www.ahdictionary.com*. Retrieved 2025-02-06.
11. Halmos 1960, p. 2.
12. Marek Capinski; Peter E. Kopp (2004). *Measure, Integral and Probability*. Springer Science & Business Media. p. 2. ISBN 978-1-85233-781-0.
13. "Set Symbols". *www.mathsisfun.com*. Retrieved 2020-08-19.
14. Stoll, Robert (1974). *Sets, Logic and Axiomatic Theories*. W. H. Freeman and Company. pp. 5. ISBN 9780716704577.
15. Aggarwal, M.L. (2021). "1. Sets". *Understanding ISC Mathematics Class XI*. Vol. 1. Arya Publications (Avichal Publishing Company). p. A=3.
16. Sourendra Nath, De (January 2015). "Unit-1 Sets and Functions: 1. Set Theory". *Chhaya Ganit (Ekadash Shreni)*. Scholar Books Pvt. Ltd. p. 5.
17. Halmos 1960, p. 8.
18. K.T. Leung; Doris Lai-chue Chen (1 July 1992). *Elementary Set Theory, Part I/II*. Hong Kong University Press. p. 27. ISBN 978-962-209-026-2.
19. A. Kanamori, "The Empty Set, the Singleton, and the Ordered Pair", p.278. *Bulletin of Symbolic Logic* vol. 9, no. 3, (2003). Accessed 21 August 2023.
20. Charles Roberts (24 June 2009). *Introduction to Mathematical Proofs: A Transition*. CRC Press. p. 45. ISBN 978-1-4200-6956-3.
21. Johnson, David; Johnson, David B.; Mowry, Thomas A. (June 2004). *Finite Mathematics: Practical Applications* (Docutech ed.). W. H. Freeman. p. 220. ISBN 978-0-7167-6297-3.
22. Bello, Ignacio; Kaul, Anton; Britton, Jack R. (29 January 2013). *Topics in Contemporary Mathematics*. Cengage. p. 47. ISBN 978.
23. Epp, Susanna S. (4 August 2010). *Discrete Mathematics with Applications*. Cengage. p. 13. ISBN 978-0-495-39132-6.
24. Maurer, Stephen B.; Ralston, Anthony (21 January 2005). *Discrete Algorithmic Mathematics*. CRC Press. p. 11. ISBN 978-1-4398-6375-6.
25. "Introduction to Sets". *www.mathsisfun.com*. Retrieved 2020-08-19.
26. Van Dalen, D.; Doets, H. C.; De Swart, H. (9 May 2014). *Sets: Naïve, Axiomatic and Applied: A Basic Compendium with Exercises for Use in Set Theory for Non-Logicians, Working and Teaching Mathematicians and Students*. Elsevier Science. p. 1. ISBN 978-1-4831-5039-0.
27. Basta, Alfred; DeLong, Stephan; Basta, Nadine (1 January 2013). *Mathematics for Information Technology*. Cengage. p. 3. ISBN 978-1-285-60843-3.
28. Bracken, Laura; Miller, Ed (15 February 2013). *Elementary Algebra*. Cengage. p. 36. ISBN 978-0-618-95134-5.
29. Frank Ruda (6 October 2011). *Hegel's Rabble: An Investigation into Hegel's Philosophy of Right*. Bloomsbury Publishing. p. 151. ISBN 978-1-4411-7413-0.
30. John F. Lucas (1990). *Introduction to Abstract Mathematics*. Rowman & Littlefield. p. 108. ISBN 978-0-912675-73-2.
31. Weisstein, Eric W. "Set". *Wolfram MathWorld*. Retrieved 2020-08-19.
32. Ralph C. Steinlage (1987). *College Algebra*. West Publishing Company. ISBN 978-0-314-29531-6.
33. Felix Hausdorff (2005). *Set Theory*. American Mathematical Soc. p. 30. ISBN 978-0-8218-3835-8.
34. Halmos 1960, p. 3.
35. Tanton, James (2005). "Set theory". *Encyclopedia of Mathematics*. New York: Facts On File. pp. 460–61. ISBN 0-8160-5124-0.
36. Halmos 1960, p. 19.
37. Halmos 1960, p. 20.
38. Yiannis N. Moschovakis (1994). *Notes on Set Theory*. Springer Science & Business Media. ISBN 978-3-540-94180-4.
39. Karl J. Smith (7 January 2008). *Mathematics: Its Power and Utility*. Cengage Learning. p. 401. ISBN 978-0-495-38913-2.
40. John Stillwell (16 October 2013). *The Real Numbers: An Introduction to Set Theory and Analysis*. Springer Science & Business Media. ISBN 978-3-319-01577-4.
41. Cantor, Georg (1878). "Ein Beitrag zur Mannigfaltigkeitslehre". *Journal für die Reine und Angewandte Mathematik*. 1878 (84): 242–258. doi:10.1515/crll.1878.84.242 (inactive 1 November 2024).
42. David Tall (11 April 2006). *Advanced Mathematical Thinking*. Springer Science & Business Media. p. 211. ISBN 978-0-306-47203-9.
43. Cohen, Paul J. (December 15, 1963a). "The Independence of the Continuum Hypothesis". *Proceedings of the National Academy of Sciences of the United States of America*. 50 (6): 1143–1148. Bibcode:1963PNAS...50.1143C. doi:10.1073/pnas.50.6.1143. JSTOR 71858. PMC 221287. PMID 16578557.
44. Gödel 1938.
45. Cohen 1963b.

13. 参考文献

• Dauben, Joseph W. (1979). *Georg Cantor: His Mathematics and Philosophy of the Infinite*. Boston: Harvard University Press. ISBN 0-691-02447-2.
• Halmos, Paul R. (1960). *Naive Set Theory*. Princeton, N.J.: Van Nostrand. ISBN 0-387-90092-6.
• Stoll, Robert R. (1979). *Set Theory and Logic*. Mineola, N.Y.: Dover Publications. ISBN 0-486-63829-4.
• Velleman, Daniel (2006). *How To Prove It: A Structured Approach*. Cambridge University Press. ISBN 0-521-67599-5.
• Gödel, Kurt (9 November 1938). "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". *Proceedings of the National Academy of Sciences of the United States of America*. 24 (12): 556–557. Bibcode:1938PNAS...24..556G. doi:10.1073/pnas.24.12.556. PMC 1077160. PMID 16577857.
• Cohen, Paul (1963b). "The Independence of the Axiom of Choice" (PDF). *Stanford University Libraries*. Archived (PDF) from the original on 2022-10-09. Retrieved 2019-03-22.

14. 外部链接

• 维基词典中的集合定义
• 康托尔的《Beiträge zur Begründung der transfiniten Mengenlehre》（德文版）