光滑函数（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在数学分析中，函数的光滑性是一个由其定义域上连续导数的阶数（可微类，differentiability class）来衡量的性质。\(^\text{[1]}\)

　　 一个属于 $C^k$ 类的函数，意味着它至少是 $k$ 阶光滑的；换句话说，$C^k$ 类函数是在其定义域上具有连续的 $k$ 阶导数的函数。

　　 一个属于 $C^\infty$ 类的函数（也称为 $C^\infty$ 函数，读作 “C-infinity function”），是一个无穷可微函数，即拥有所有阶数导数的函数（这也意味着所有这些导数都是连续的）。

　　 通常情况下，术语光滑函数指的就是一个 $C^\infty$ 函数。但在某些问题的语境中，它也可能表示 “具有足够阶可微性” 的函数。

1. 可微类

　　 可微类是根据函数导数的性质对函数进行分类的一种方式，它衡量的是函数存在并且连续的最高阶导数的阶数。

　　 考虑实数轴上的一个开集 $U$，以及一个定义在 $U$ 上、取实值的函数 $f$。设 $k$ 是一个非负整数。如果函数 $f$ 的各阶导数 $f', f'', \dots, f^{(k)}$ 都存在并且在 $U$ 上连续，则称函数 $f$ 属于 $C^k$ 类。如果 $f$ 在 $U$ 上是 $k$ 阶可微的，那么它至少属于 $C^{k-1}$ 类，因为它的 $f', f'', \dots, f^{(k-1)}$ 都在 $U$ 上连续。如果函数 $f$ 在 $U$ 上有任意阶导数，则称它是无穷可微的、光滑的，或者是 $C^\infty$ 类。这意味着它的所有导数在 $U$ 上都是连续函数。\(^\text{[2]}\) 如果函数 $f$ 是光滑的（即 $f \in C^\infty$），并且它在定义域内任意一点的 Taylor 级数在该点的某个邻域内收敛并等于函数本身，则称 $f$ 属于 $C^\omega$ 类，也称为解析函数。存在一些函数是光滑但不是解析的，因此 $C^\omega$ 严格包含在 $C^\infty$ 之内。凸起函数就是这种性质的例子。

　　 换句话说：$C^0$ 类是所有连续函数的集合；$C^1$ 类是所有一阶导数存在且连续的函数，这类函数称为连续可微函数。因此，$C^1$ 函数正好是导数存在且导数属于 $C^0$ 类的函数。一般来说，可递归地定义这些类：$C^0$ 类：所有连续函数的集合；$C^k$ 类（$k>0$）：所有可微函数的集合，其导数属于 $C^{k-1}$ 类。由此可以得出：对于每个 $k>0$，有 $C^k \subset C^{k-1},$ 且严格包含（$C^k \subsetneq C^{k-1}$）。无穷可微函数的类 $C^\infty$ 是所有非负整数 $k$ 的 $C^k$ 类的交集。

示例

　　 示例：连续（C⁰）但不可微

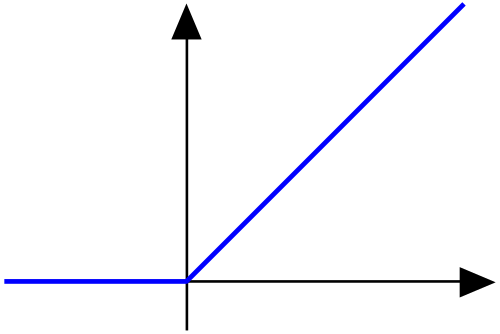
　　 函数 $$ f(x)= \begin{cases} x, & x \ge 0,\\ 0, & x < 0 \end{cases}~ $$ 是连续的，但在 $x = 0$ 处不可微，因此它属于 $C^0$ 类，但不属于 $C^1$ 类。

　　 示例：有限次可微函数（Cᵏ）

　　 对于每个偶数整数 $k$，函数 $$ f(x) = |x|^{k+1}~ $$ 在所有 $x$ 上都是连续且 $k$ 次可微的。然而，在 $x = 0$ 处，$f$ 并不是 $(k+1)$ 次可微的，因此 $f$ 属于 $C^k$ 类，但不属于任意 $C^j$ 类（其中 $j > k$）。

　　 示例：可微但导数不连续（非 $C^1$）

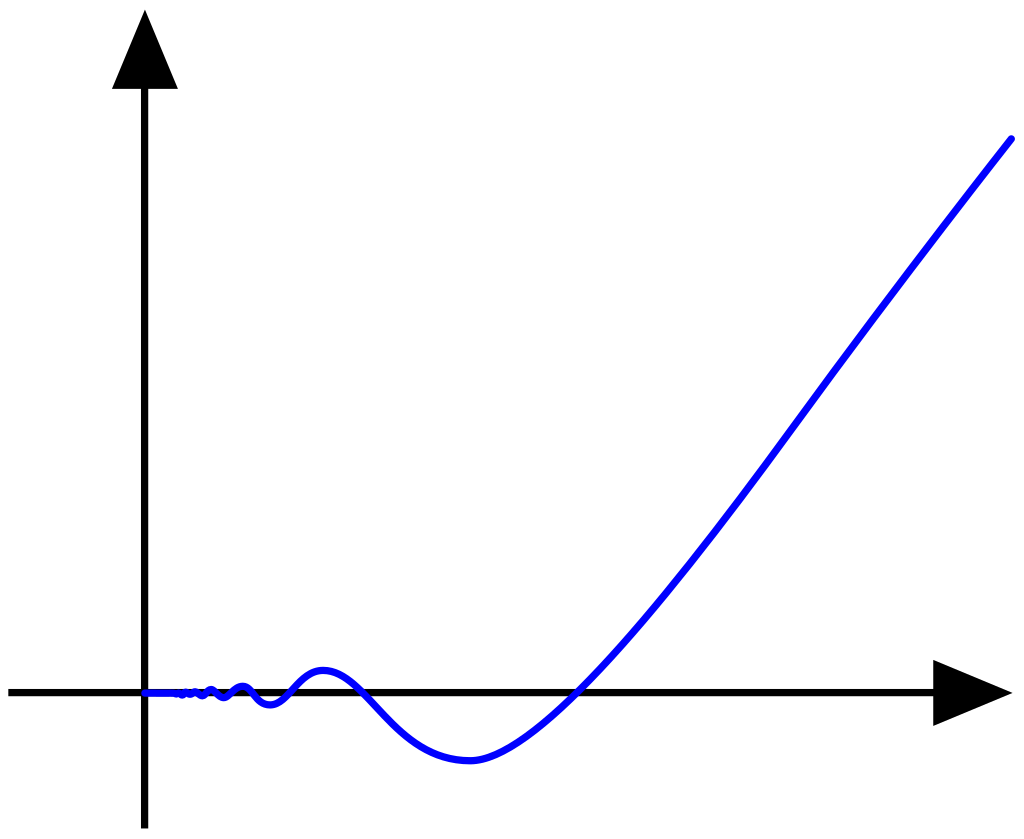
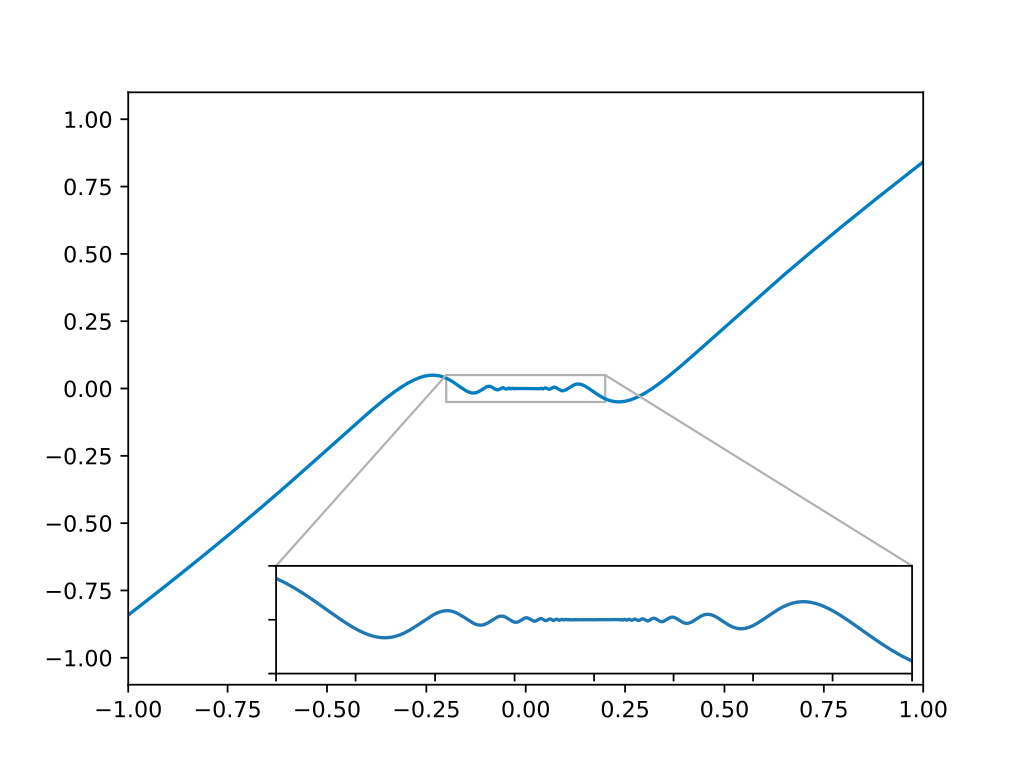
　　 函数 $$ g(x) = \begin{cases} x^2 \sin\left(\frac{1}{x}\right), & x \neq 0,\\ 0, & x = 0 \end{cases}~ $$ 是可微的，其导数为 $$ g'(x) = \begin{cases} -\cos\left(\frac{1}{x}\right) + 2x \sin\left(\frac{1}{x}\right), & x \neq 0,\\ 0, & x = 0 \end{cases}~ $$ 由于 $ \cos\left(1/x\right) $ 在 $x \to 0$ 时振荡，$g'(x)$ 在 0 处不连续。因此，$g(x)$ 是可微的，但不属于 $C^1$ 类。

　　 示例：可微但非 Lipschitz 连续

　　 函数 $$ h(x) = \begin{cases} x^{4/3} \sin\left(\frac{1}{x}\right), & x \neq 0,\\ 0, & x = 0 \end{cases}~ $$ 是可微的，但它的导数在某些紧集上无界。 因此，$h$ 是一个可微但不是局部 Lipschitz 连续的函数示例。

　　 示例：解析函数（$C^\omega$）

　　 指数函数 $e^x$ 是解析的，因此属于 $C^\omega$ 类（其中 $\omega$ 是最小的超限序数）。三角函数在其定义域内也是解析的，因为它们是复指数函数 $e^{ix} \quad \text{和} \quad e^{-ix}$ 的线性组合。

　　 示例：光滑函数（$C^\infty$）但非解析函数（$C^\omega$）

　　 凸起函数 $$ f(x) = \begin{cases} e^{-\frac{1}{1-x^2}}, & |x| < 1,\\ 0, & \text{其他情况} \end{cases}~ $$ 是光滑的，因此属于 $C^\infty$ 类，但在 $x = \pm 1$ 处不是解析的，因此不属于 $C^\omega$ 类。函数 $f$ 是一个具有紧支集的光滑函数的例子。

多变量可微类

　　 一个函数 $f: U \subseteq \mathbb{R}^n \to \mathbb{R}$，定义在 $\mathbb{R}^n$ 的开集 $U$ 上，若对于每组非负整数 $\alpha_1, \alpha_2, \ldots, \alpha_n$ 满足 $\alpha = \alpha_1 + \alpha_2 + \cdots + \alpha_n \le k$，所有的偏导数 $$ \frac{\partial^\alpha f}{\partial x_1^{\alpha_1}\,\partial x_2^{\alpha_2}\,\cdots\,\partial x_n^{\alpha_n}}(y_1, y_2, \ldots, y_n)~ $$ 都存在且在 $U$ 上连续，则称函数 $f$ 在 $U$ 上是 $C^k$ 类函数。等价地，如果 $f$ 的第 $k$ 阶 Fréchet 导数在 $U$ 的每一点都存在且连续，那么 $f$ 也是 $C^k$ 类的。如果函数 $f$ 在 $U$ 上连续，则称它是 $C$ 类或 $C^0$ 类函数。若 $f$ 是 $C^1$ 类函数，则称它是连续可微的。

　　 一个函数 $f: U \subset \mathbb{R}^n \to \mathbb{R}^m$，定义在 $\mathbb{R}^n$ 的开集 $U$ 上，如果它的每一个分量函数 $$ f_i(x_1, x_2, \ldots, x_n) = (\pi_i \circ f)(x_1, x_2, \ldots, x_n) = \pi_i(f(x_1, x_2, \ldots, x_n)), \quad i=1,2,3,\ldots,m,~ $$ 都是 $C^k$ 类的（其中 $\pi_i: \mathbb{R}^m \to \mathbb{R}$ 是自然投影，定义为 $\pi_i(x_1, x_2, \ldots, x_m) = x_i$），则称 $f$ 在 $U$ 上是 $C^k$ 类函数。如果 $f$ 在 $U$ 上连续，或者等价地，所有分量 $f_i$ 都是连续的，则称 $f$ 是 $C$ 类或 $C^0$ 类函数。

$C^k$ 函数空间

　　 设 $D$ 是实数轴上的一个开集。所有定义在 $D$ 上的 $C^k$ 实值函数的集合构成一个 Fréchet 向量空间，其拓扑由一列半范数族给出： $$ p_{K,m} = \sup_{x \in K} \big| f^{(m)}(x) \big|,~ $$ 其中 $K$ 是一列逐渐增大的紧集，它们的并集是 $D$，而 $m = 0, 1, \dots, k$。

　　 定义在 $D$ 上的 $C^\infty$ 函数的集合同样构成一个Fréchet 空间。使用的方法与上面相同，只是此时 $m$ 取遍所有非负整数。

　　 这些空间在许多需要函数具有某一阶导数的应用中自然出现；然而，尤其是在研究偏微分方程时，使用Sobolev 空间有时会更加有用。

2. 连续性

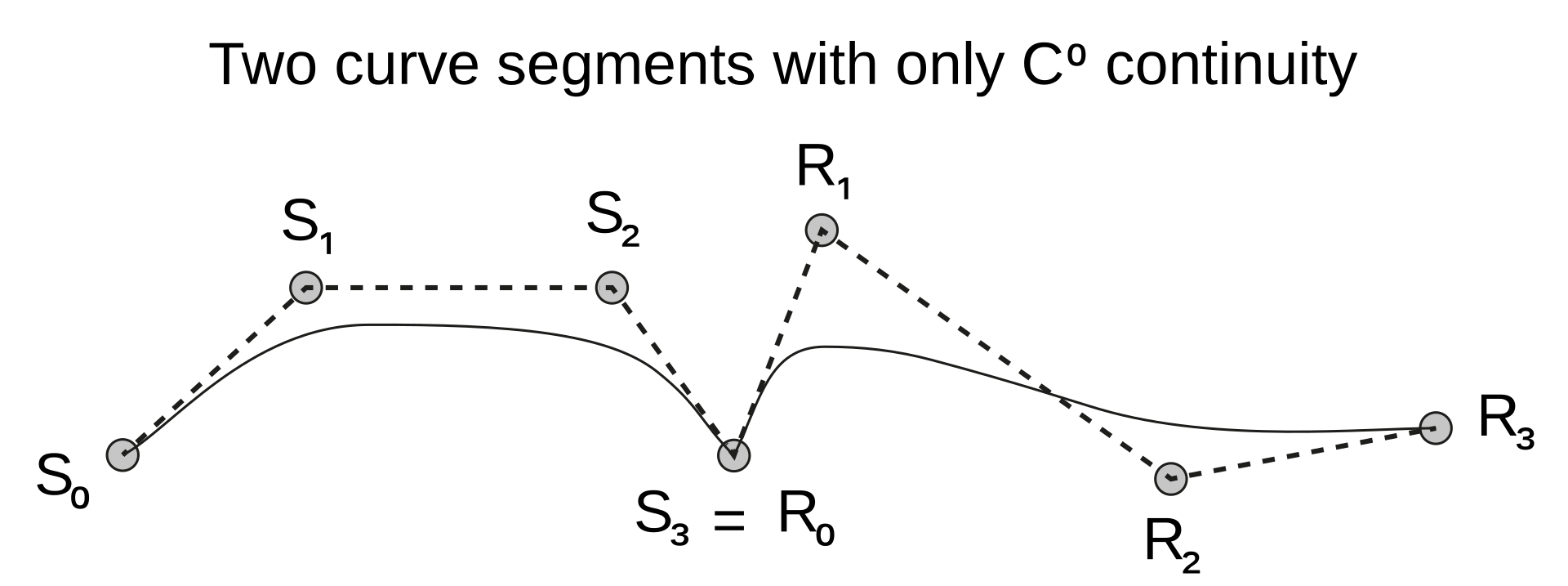
　　 参数连续性（parametric continuity，$C^k$）和几何连续性（geometric continuity，$G^n$）这两个术语是由 Brian Barsky 提出的，用来说明可以通过放宽参数沿曲线运动速度的限制来衡量曲线的光滑程度。\(^\text{[4][5][6]}\)

参数连续性

　　 参数连续性（$C^k$）是应用于参数曲线的一个概念，用于描述曲线沿长度方向参数值变化的平滑程度。一个（参数）曲线 $s: [0,1] \to \mathbb{R}^n$ 称为 $C^k$ 类，如果 $\frac{d^k s}{dt^k}$ 在区间 $[0,1]$ 上存在并且连续，其中端点 $0$ 和 $1$ 处的导数取单侧导数（在 $0$ 处取右导数，在 $1$ 处取左导数）。

　　 作为该概念的一个实际应用，描述物体随时间运动的曲线必须至少具有 $C^1$ 连续性，并且它的一阶导数可微，才能保证物体具有有限的加速度。而对于更平滑的运动，例如电影拍摄中相机的运动路径，则需要更高阶的参数连续性。

　　 参数连续性的阶数

　　 参数连续性的不同阶数可以描述如下：\(^\text{[7]}\)

• $C^0$：零阶导数连续（曲线本身连续）
• $C^1$：零阶和一阶导数连续
• $C^2$：零阶、一阶和二阶导数连续
• $C^n$：从零阶到第 $n$ 阶导数都连续

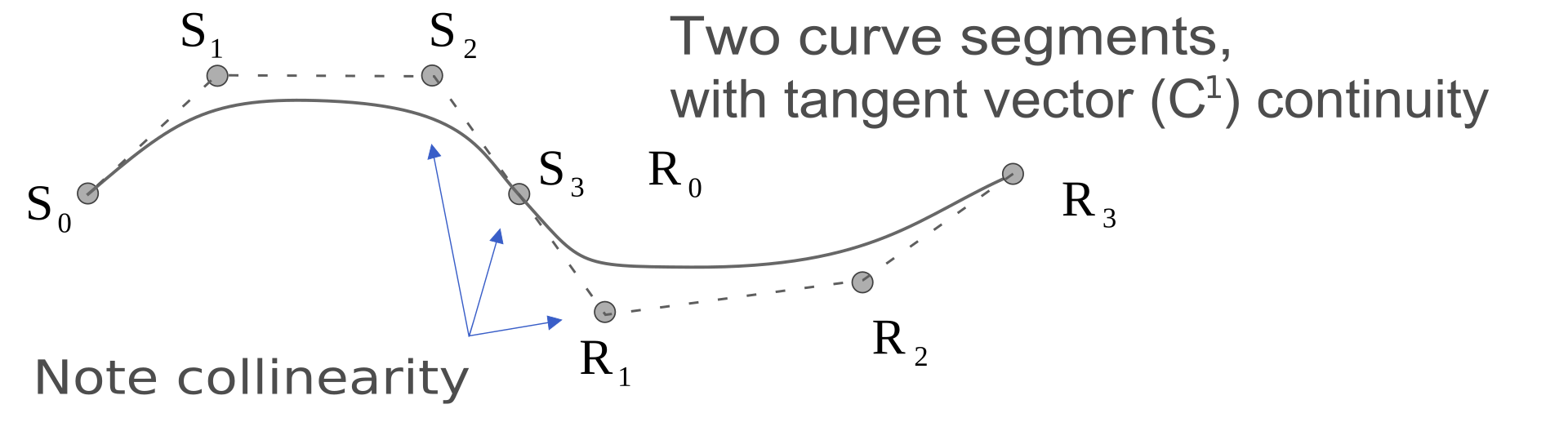
几何连续性

　　 一条曲线或曲面可以被描述为具有 $G^n$ 连续性，其中 $n$ 表示光滑程度的递增量。考虑曲线上某个点两侧的曲线片段：

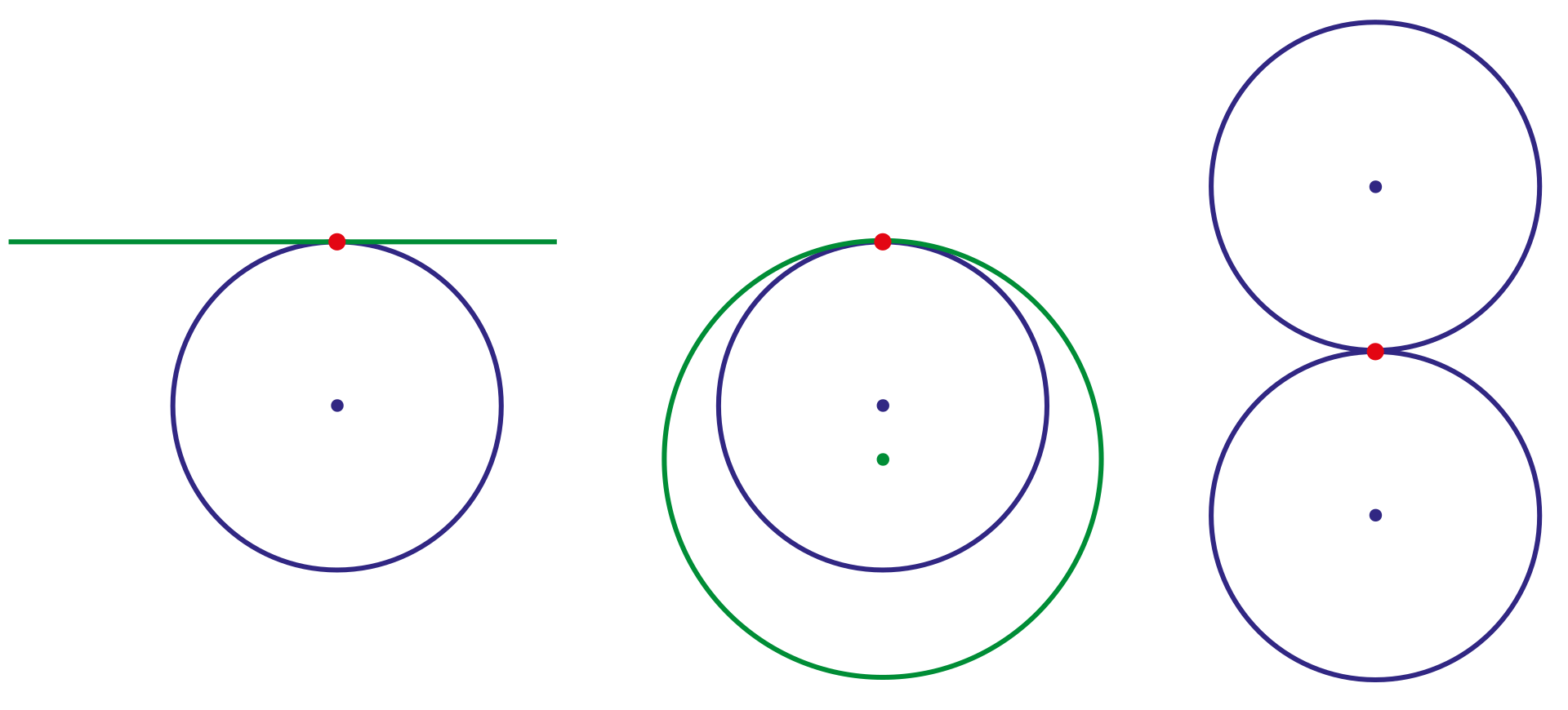
• $G^0$：两段曲线在连接点处相接触。
• $G^1$：两段曲线在连接点处还共享相同的切线方向。
• $G^2$：两段曲线在连接点处还共享相同的曲率中心。

　　 一般来说，如果曲线可以重新参数化，使其具有 $C^n$（参数意义上的）连续性，那么它们就具有 $G^n$ 连续性。\(^\text{[8][9]}\) 重新参数化后的曲线在几何上与原曲线完全相同，只是参数发生了改变。

　　 等价地，若两个向量函数 $f(t)\quad \text{和} \quad g(t)$ 满足 $f(1) = g(0)$，则当它们在连接点处满足称为 Beta 约束 的一组方程时，它们在该点具有 $G^n$ 连续性： $$ \begin{aligned} g^{(1)}(0) &= \beta_1 f^{(1)}(1)\\ g^{(2)}(0) &= \beta_1^{2} f^{(2)}(1) + \beta_2 f^{(1)}(1)\\ g^{(3)}(0) &= \beta_1^{3} f^{(3)}(1) + 3\beta_1 \beta_2 f^{(2)}(1) + \beta_3 f^{(1)}(1)\\ g^{(4)}(0) &= \beta_1^{4} f^{(4)}(1) + 6\beta_1^{2} \beta_2 f^{(3)}(1) + (4\beta_1\beta_3 + 3\beta_2^{2}) f^{(2)}(1) + \beta_4 f^{(1)}(1) \end{aligned}~ $$ 其中，$\beta_2$、$\beta_3$ 和 $\beta_4$ 是任意的，但 $\beta_1$ 被限制为正数。\(^\text{[8: 65 ]}\) 当 $n = 1$ 时，上式可以简化为 $f'(1) \neq 0$ 以 $f'(1) = k g'(0)$，其中 $k > 0$ 是一个标量（即两个向量的方向相同，但大小不一定相同）。

　　 虽然很明显，要让曲线看起来光滑至少需要 $G^1$ 连续性，但为了获得更好的美观效果，例如建筑设计和跑车设计中所追求的效果，往往需要更高等级的几何连续性。例如，车身上的反光效果只有在车身表面具有 $G^2$ 连续性时才会显得平滑。

　　 一个圆角矩形（四个角为 90 度圆弧）具有 $G^1$ 连续性，但不具备 $G^2$ 连续性。类似地，一个圆角立方体（角是球体的八分体，边是四分之一圆柱）也是如此。如果需要一条具有 $G^2$ 连续性且可编辑的曲线，通常会选择三次样条曲线；这种曲线在工业设计中被广泛应用。

3. 其他概念

与解析性的关系

　　 虽然所有解析函数在其解析域上都是 “光滑的”（即所有阶导数都是连续的），但如前面提到的凸起函数所示，反之在实数域上并不成立：存在光滑但并非解析的实函数。一些既光滑又在任何点都不解析的简单函数示例可以通过傅里叶级数构造出来；另一个例子是 Fabius 函数。尽管看起来这种函数似乎是例外，但事实上，解析函数在光滑函数中只占很小的比例；更严格地说，解析函数在光滑函数空间中构成了一个稀疏子集。此外，对于实数轴上的任意开子集 $A$，都存在一些光滑函数，它们仅在 $A$ 上解析，而在其他地方都不解析。

　　 这种情形可以类比实数轴上超越数的普遍存在性。在实数轴和光滑函数的集合中，我们最先想到的例子（代数数/有理数与解析函数）通常表现得更加 “规整”，但实际上，超越数和在任何点都不解析的光滑函数才占据了 “满测度”（其补集是稀疏的）。

　　 这种情况与复函数理论形成了鲜明对比。如果一个复函数在某个开集上仅可微一次，那么它在该开集上不仅是无穷可微的，而且还是解析的。

光滑的单位分解

　　 具有指定闭支集的光滑函数常用于构造光滑的单位分解（参见 partition of unity 和 topology glossary）；这种构造在研究光滑流形时至关重要，例如用来证明黎曼度量可以从局部定义推广到整体。一个简单的情形是实数轴上的凸起函数，即一个光滑函数 $f$，在区间 $[a,b]$ 之外取值为 0，并且在区间内部满足： $$ f(x) > 0, \quad a < x < b~ $$ 如果实数轴上有多个相互重叠的区间，可以在每个区间上构造一个这样的凸起函数，并在半无限区间 $(-\infty, c]$ 和 $[d, +\infty)$ 上也定义相应的函数，使得它们的和在整个实数轴上恒等于 1。

　　 需要注意的是，这种单位分解的构造不适用于全纯函数；它们在存在性和解析延拓上的不同表现，正是层论产生的根源之一。相比之下，光滑函数的层往往不携带太多拓扑信息。

流形上的光滑函数及流形之间的光滑映射

　　 给定一个维度为 $m$ 的光滑流形 $M$，以及其图册 $\mathfrak{U} = \{(U_\alpha, \phi_\alpha)\}_\alpha$，若映射 $f: M \to \mathbb{R}$ 满足：对于每个 $p \in M$，存在一个图册中的图 $(U, \phi) \in \mathfrak{U}$，使得 $p \in U$，且复合映射 $f \circ \phi^{-1} : \phi(U) \to \mathbb{R}$ 是从 $\mathbb{R}^m$ 的某个邻域到 $\mathbb{R}$ 的光滑函数（即所有阶数不超过某一阶的偏导数均连续），那么称 $f$ 是定义在 $M$ 上的光滑函数。光滑性可以通过包含 $p$ 的任意一张图来验证，因为不同图之间的过渡函数本身是光滑的。这保证了如果 $f$ 在某张图下在 $p$ 附近是光滑的，那么它在包含 $p$ 的任意其他图下也同样是光滑的。

　　 若 $F: M \to N$ 是从 $M$ 到 $n$ 维流形 $N$ 的一个映射，则当且仅当对于每个 $p \in M$，存在包含 $p$ 的图 $(U, \phi)$ 和包含 $F(p)$ 的图 $(V, \psi)$，使得 $F(U) \subset V$，且复合映射 $\psi \circ F \circ \phi^{-1} : \phi(U) \to \psi(V)$ 是从 $\mathbb{R}^m$ 到 $\mathbb{R}^n$ 的光滑函数时，称 $F$ 是光滑映射。

　　 流形之间的光滑映射可以诱导切空间之间的线性映射：对于 $F: M \to N$，在每个点 $p \in M$，其推前（pushforward 或微分）将 $p$ 处的切向量映射到 $F(p)$ 处的切向量：$F_{*,p}: T_p M \to T_{F(p)} N$。在切丛的层面上，推前是一个向量丛同态：$F_*: TM \to TN$。推前的对偶是拉回，它将 $N$ 上的余向量 “拉回” 到 $M$ 上的余向量，并将 $k$-形式拉回为 $k$-形式：$F^*: \Omega^k(N) \to \Omega^k(M)$。通过这种方式，流形之间的光滑函数可以传递局部数据，例如向量场和微分形式，将它们从一个流形运送到另一个流形，或者映射到欧几里得空间，以便在该空间中进行如积分等容易计算的操作。

　　 沿光滑函数的原像和推前一般情况下并不一定构成流形，除非有附加条件。对于正则点的原像（即微分在原像上不为零的点），原像确实是流形；这就是原像定理（类似地，沿嵌入映射的推前结果也是流形。\(^\text{[10]}\)

流形子集之间的光滑函数

　　 对于流形的任意子集，也有相应的光滑映射概念。如果 $f: X \to Y$ 是一个函数，其定义域和值域分别是流形的子集 $X \subseteq M\quad \text{和} \quad Y \subseteq N$，则称 $f$ 是光滑的，如果对于所有 $x \in X$，都存在一个包含 $x$ 的开集 $U \subseteq M$，以及一个光滑函数 $F: U \to N$，使得对于所有 $p \in U \cap X$，都有 $F(p) = f(p)$。

4. 参见

• Discontinuity– 对不连续点的数学分析
• Hadamard's lemma
• Non-analytic smooth function – 光滑但非解析的数学函数
• Quasi-analytic function
• Singularity (mathematics) – 函数、曲线或其他数学对象不再表现为常规行为的点
• Sinuosity – 波浪状函数中两点之间弧长与直线距离的比值
• Smooth scheme
• Smooth number – 仅有小质因子的整数（数论）
• Smoothing – 将近似函数拟合到数据的方法
• Spline – 由多项式分段定义的数学函数
• Sobolev mapping

5. 参考文献

1. Weisstein, Eric W. "Smooth Function". mathworld.wolfram.com. Archived from the original on 2019-12-16. Retrieved 2019-12-13.
2. Warner, Frank W. (1983). Foundations of Differentiable Manifolds and Lie Groups. Springer. p. 5 [Definition 1.2]. ISBN 978-0-387-90894-6. Archived from the original on 2015-10-01. Retrieved 2014-11-28.
3. Henri Cartan (1977). Cours de calcul différentiel. Paris: Hermann.
4. Barsky, Brian A. (1981). The Beta-spline: A Local Representation Based on Shape Parameters and Fundamental Geometric Measures* (Ph.D.). University of Utah, Salt Lake City, Utah.
5. Brian A. Barsky (1988). Computer Graphics and Geometric Modeling Using Beta-splines. Springer-Verlag, Heidelberg. ISBN 978-3-642-72294-3.
6. Richard H. Bartels; John C. Beatty; Brian A. Barsky (1987). An Introduction to Splines for Use in Computer Graphics and Geometric Modeling. Morgan Kaufmann. Chapter 13. Parametric vs. Geometric Continuity. ISBN 978-1-55860-400-1.
7. van de Panne, Michiel (1996). "Parametric Curves". Fall 1996 Online Notes. University of Toronto, Canada. Archived from the original on 2020-11-26. Retrieved 2019-09-01.
8. Barsky, Brian A.; DeRose, Tony D. (1989). "Geometric Continuity of Parametric Curves: Three Equivalent Characterizations". IEEE Computer Graphics and Applications. 9 (6): 60–68. doi:10.1109/38.41470. S2CID 17893586.
9. Hartmann, Erich (2003). "Geometry and Algorithms for Computer Aided Design" (PDF). Technische Universität Darmstadt. p. 55. Archived (PDF) from the original on 2020-10-23. Retrieved 2019-08-31.
10. Guillemin, Victor; Pollack, Alan (1974). Differential Topology. Englewood Cliffs: Prentice-Hall. ISBN 0-13-212605-2.