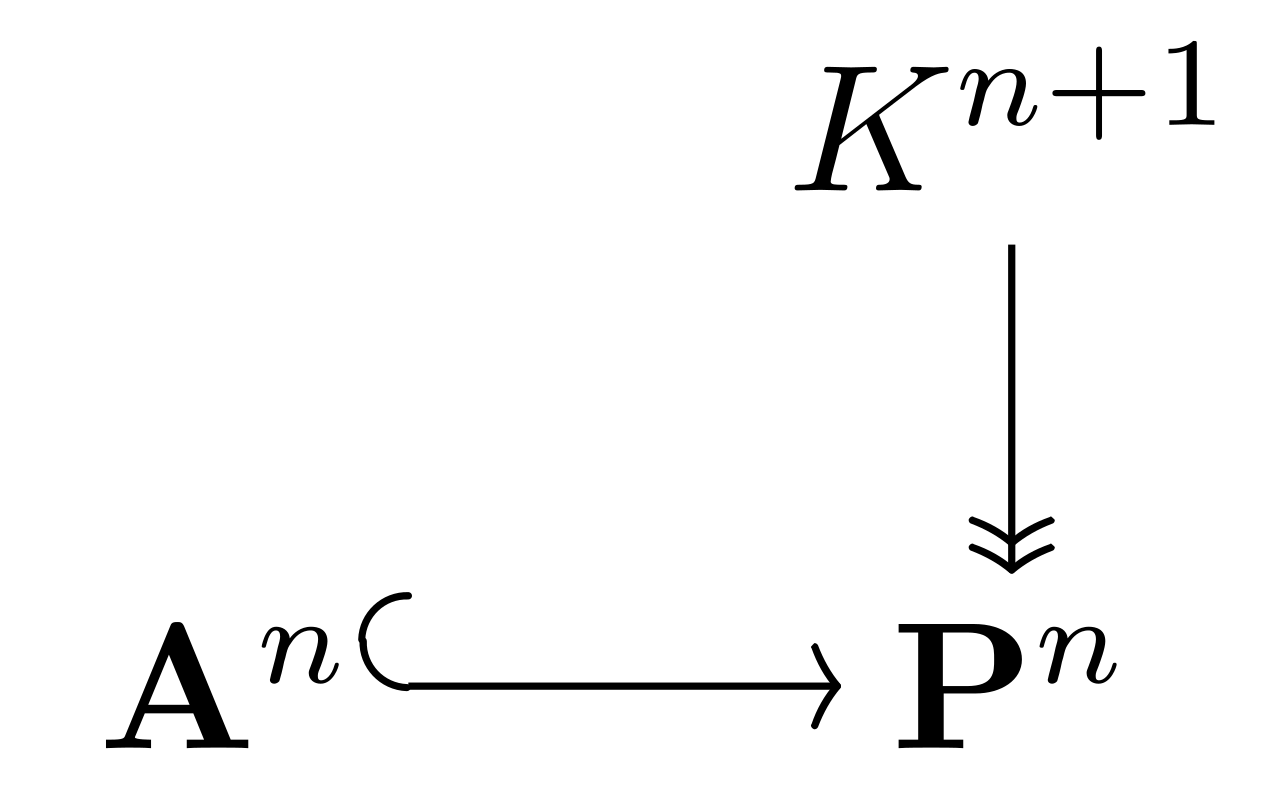仿射空间（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

图
图 1：在 $\mathbb{R}^3$ 中，蓝色的上平面 $P_2$ 不是一个向量子空间，因为：$\mathbf{0} \notin P_2$；$\mathbf{a} + \mathbf{b} \notin P_2$。因此，$P_2$ 是一个仿射子空间。它的方向（即与该仿射子空间关联的线性子空间）是绿色的下平面 $P_1$，这个平面是一个向量子空间。虽然向量 $\mathbf{a}$ 和 $\mathbf{b}$ 都属于 $P_2$，但它们的差向量是一个位移向量，它不属于 $P_2$，而是属于向量空间 $P_1$。

　　 在数学中，仿射空间是一种几何结构，它推广了欧几里得空间的一些性质，但这些性质与距离和角度测量无关，仅保留了平行性和平行线段长度比例等相关特性。仿射空间是仿射几何的基本背景。

　　 与欧几里得空间类似，仿射空间中的基本对象称为点，它们可以看作空间中的 “位置”，没有大小或形状，即零维对象。通过任意两点，可以画出一条无限延伸的直线（一维点集）；通过任意不共线的三点，可以画出一个平面（二维点集）；更一般地，任意 $k+1$ 个处于一般位置的点，可以确定一个 $k$ 维平面或仿射子空间。仿射空间的一个显著特征是平行线的概念：同一平面内的两条平行直线永不相交；同一平面内的非平行直线则必定在某一点相交。并且，对于任意一条直线和空间中的任意一点，总能画出一条通过该点且与原直线平行的直线。所有相互平行的直线属于同一个方向的等价类。

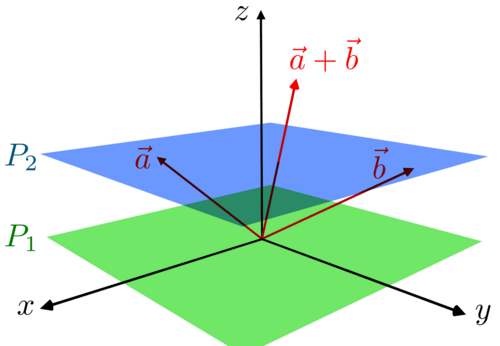
　　 与向量空间中的向量不同，仿射空间中没有一个特定的点作为原点。在仿射空间中：没有预定义的 “点与点相加” 或 “点与数相乘” 的概念。然而，对于任意一个仿射空间，可以通过两点之间的差来构造一个关联向量空间。这些差向量被称为：自由向量，位移向量，平移向量或简称平移 \(^\text{[1]}\)。同样，将一个位移向量加到某个点上是有意义的，这会生成一个新的点，即从原点沿该向量平移后的点。虽然点不能被随意相加，但可以取点的仿射组合：即系数和为 1 的加权和，这会产生另一个点。这些系数定义了经过这些点所在平面的重心坐标系。

　　 任意向量空间都可以被看作一个仿射空间，这相当于 “忘记零向量的特殊角色”。在这种情况下：向量空间中的元素既可以看作仿射空间中的点，也可以看作位移向量（平移）。当把零向量看作一个点时，它就被称为原点。将一个固定向量加到向量空间的某个线性子空间上，可以得到这个向量空间的一个仿射子空间。我们通常说，这个仿射子空间是通过某个平移向量将该线性子空间从原点平移得到的。在有限维情形下：这样的仿射子空间就是某个非齐次线性系统的解集；该仿射空间的位移向量则是对应齐次线性系统的解集，这是一个线性子空间。相比之下，线性子空间总是包含向量空间的原点。

　　 仿射空间的维数定义为其平移向量空间的维数：一维仿射空间称为仿射直线；二维仿射空间称为仿射平面；在 $n$ 维的仿射空间或向量空间中，维数为 $n-1$ 的仿射子空间称为仿射超平面。

1. 非正式描述

图
图 2：从 Alice 和 Bob 的视角来看原点的位置：Alice 视角下的向量计算用红色表示；Bob 视角下的向量计算用蓝色表示。

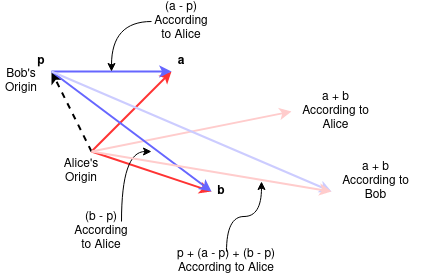
　　 仿射空间就是一个向量空间，在 “忘记哪个点是原点” 之后所剩下的结构。正如法国数学家 Marcel Berger 所说：“仿射空间不过是一个向量空间，我们试图通过加入平移，把原点从线性映射的结构中抹去。”\(^\text{[2]}\) 想象这样一个情境：Alice 知道某个点是真正的原点；而 Bob 认为另一个点 $p$ 才是原点。现在要把两个向量 $a$ 和 $b$ 相加：Bob 从点 $p$ 各自画一条箭头指向 $a$ 和 $b$，再通过平行四边形法则求出他认为的 $a + b$；但 Alice 知道，他实际上计算的是： $$ p + (a - p) + (b - p)~ $$ 同样地，Alice 和 Bob 也可以分别计算 $a$ 和 $b$ 的任意线性组合，或者某个有限向量集合的线性组合。一般情况下，他们会得到不同的结果。然而，如果某个线性组合的系数和等于 1，那么他们会得到完全相同的结果。

　　 例如：如果 Alice 走到了： $$ \lambda a + (1 - \lambda)b~ $$ 那么 Bob 会走到： $$ p + \lambda(a - p) + (1 - \lambda)(b - p) = \lambda a + (1 - \lambda)b~ $$ 只要满足：$\lambda + (1 - \lambda) = 1$ 无论他们各自认为哪个点是原点，都会用相同的线性组合描述同一个点。

　　 因此：只有 Alice 知道完整的线性结构；但 Alice 和 Bob 都知道相同的 “仿射结构”，即 “系数和等于 1 的线性组合” 的取值。任何一个具备这种 “仿射结构” 的集合，就是一个仿射空间。

2. 定义

　　 虽然仿射空间可以用公理化的方式来定义（见下文 § 公理部分），这种方法类似于欧几里得在《几何原本》中对欧几里得空间的定义，但为了方便，现代的大多数资料都会基于成熟的向量空间理论来定义仿射空间。

　　 一个仿射空间由以下部分组成：一个集合 $A$；一个向量空间 $\overrightarrow{A}$；以及 $\overrightarrow{A}$ 的加法群在 $A$ 上的一个自由且传递的作用。[3]

　　 其中：$A$ 中的元素称为点；与该仿射空间关联的向量空间 $\overrightarrow{A}$ 中的元素称为向量，也可以称为平移，有时也叫自由向量。

　　 上述定义可以更明确地表示为一个映射（通常记作 “加法”）： $$ \begin{aligned} A \times \overrightarrow{A} &\;\longrightarrow\; A \\ (a, v) &\;\longmapsto\; a + v, \end{aligned}~ $$ 并且这个映射满足以下性质[4][5][6]：

  1. 右单位元：
    $$ \forall a \in A, \quad a + 0 = a,~ $$ 其中 $0$ 是关联向量空间 $\overrightarrow{A}$ 的零向量。
  2. 结合律：
    $$ \forall v, w \in \overrightarrow{A},\; \forall a \in A, \quad (a + v) + w = a + (v + w),~ $$ 这里最后的 “+” 是指在 $\overrightarrow{A}$ 中的向量加法。
  3. 自由且传递的作用：
    对于任意 $a \in A$，映射 $$ \overrightarrow{A} \;\longrightarrow\; A: \quad v \;\longmapsto\; a + v~ $$ 是一个双射。
    前两个性质只是（右）群作用基本定义。第三个性质刻画了自由且传递的作用：传递性保证了映射是 “满射”；自由性则保证了映射是 “单射”。由前两个性质，还可以推出第四个性质：
  4. 一一对应的平移：
    对于任意 $v \in \overrightarrow{A}$，映射： $$ A \;\longrightarrow\; A: \quad a \;\mapsto\; a + v~ $$ 是一个双射。
    性质 3 通常可以用以下等价形式（第 5 个性质）表述：
  5. 减法：
    对于任意 $a, b \in A$，存在唯一的 $v \in \overrightarrow{A}$，记作： $b - a$,使得：$b = a + v$.

　　 另一种表达这个定义的方式是：仿射空间是一个向量空间加法群作用下的主齐性空间。 按定义，齐性空间是带有一个传递群作用的空间；对于主齐性空间，这种传递作用还必须是自由的。

减法与魏尔公理

　　 群作用的这些性质允许在仿射空间 $A$ 中定义点对之间的减法：对于有序点对 $(b, a)$，可以得到一个属于关联向量空间 $\overrightarrow{A}$ 的向量，记作：$b - a$，或 $\overrightarrow{ab}$。这个向量被定义为满足下式的唯一向量： $$ a + (b - a) = b~ $$ 其存在性来源于群作用的传递性，而唯一性来源于群作用的自由性。

　　 这种减法满足以下两个性质，被称为魏尔公理[7]：

  1. 唯一解公理 $\forall a \in A, \;\forall v \in \overrightarrow{A}, \;\exists! b \in A, \;\text{使得 } b - a = v$
  2. 链式相加公理 $\forall a, b, c \in A, \;(c - b) + (b - a) = c - a$。

　　 此外，仿射空间还满足平行四边形性质。对于四个点 $a, b, c, d$：如果 $b - a = d - c$，那么 $c - a = d - b$；反之亦然。这是魏尔第二公理的推论，因为：$ d - a = (d - b) + (b - a) = (d - c) + (c - a)$。

　　 因此，仿射空间也可以等价地定义为：一个点集 $A$；一个向量空 $\overrightarrow{A}$；以及一个满足魏尔公理的减法运算。在这种定义下，向量加点的运算可以通过魏尔第一个公理自然地导出。

3. 仿射子空间与平行性

　　 一个仿射空间 $A$ 的仿射子空间（在某些语境下也称为线性簇、平面，或者在实数域上称为线性流形 $B$，是满足以下条件的 $A$ 的子集：若 $a \in B$，则由 $\overrightarrow{B} = \{ b - a \;\mid\; b \in B \}$ 生成的集合是关联向量空间 $\overrightarrow{A}$ 的一个线性子空间。这个性质与选取的点 $a$ 无关，因此 $B$ 本身也是一个仿射空间，其关联向量空间就是 $\overrightarrow{B}$。

　　 在仿射空间 $A$ 中，所有仿射子空间都可以写成如下形式： $$ a + V = \{ a + w \;\mid\; w \in V \},~ $$ 其中：$a$ 是 $A$ 中的某个点；$V$ 是 $\overrightarrow{A}$ 的一个线性子空间。

　　 与某个仿射子空间关联的线性子空间通常被称为它的方向。如果两个子空间的方向相同，则称它们是平行的。

　　 由此可以推广普莱费尔公理：给定一个方向 $V$，对于 $A$ 中的任意一点 $a$，都存在且仅存在一个通过 $a$ 的、方向为 $V$ 的仿射子空间，这个子空间就是：$a + V$.

　　 此外，任意一个平移映射：$A \;\to\; A :\; a \;\mapsto\; a + v$ 都会将任意仿射子空间映射为一个与原子空间平行的子空间。

　　 在某些情况下，“平行” 这个术语也用于描述：如果一个仿射子空间的方向包含于另一个仿射子空间的方向，则这两个子空间也是平行的。

4. 仿射映射

　　 设有两个仿射空间 $A$ 和 $B$，它们的关联向量空间分别为 $\overrightarrow{A}$ 和 $\overrightarrow{B}$。从 $A$ 到 $B$ 的仿射映射（affine map 或 affine homomorphism）是一个映射： $$ f: A \;\longrightarrow\; B~ $$ 该映射满足： $$ \begin{aligned} \overrightarrow{f}: \overrightarrow{A} &\;\longrightarrow\; \overrightarrow{B} \\ b - a &\;\longmapsto\; f(b) - f(a) \end{aligned}~ $$ 其中 $\overrightarrow{f}$ 是一个良定义的线性映射。“良定义” 意味着：如果 $b - a = d - c$，则必有 $f(b) - f(a) = f(d) - f(c)$。

　　 由此可以得到，对于任意一点 $a \in A$ 和任意向量 $v \in \overrightarrow{A}$： $$ f(a + v) = f(a) + \overrightarrow{f}(v).~ $$ 因此，对于仿射空间 $A$ 中的任意一点 $b$，由于存在唯一的向量 $v$ 使得 $b = a + v$，所以仿射映射 $f$ 可以由：在某个点 $a$ 上的取值以及关联的线性映射 $\overrightarrow{f}$ 完全确定。

自同态

　　 一个仿射空间 $A$ 的仿射变换或自同态，是指从该空间映射到其自身的仿射映射。一个重要的例子是平移：给定一个向量 $\overrightarrow{v}$，可以定义平移映射：$T_{\overrightarrow{v}}: A \;\longrightarrow\; A$ 它将每个点 $a \in A$ 映射为：$a \;\longmapsto\; a + \overrightarrow{v}$。另一个重要的例子是以某个点为中心的线性映射：给定：一个点 $b \in A$，以及一个线性映射 $M$，可以定义仿射映射：$L_{M,b}: A \;\longrightarrow\; A$ 使得： $$ L_{M,b}(a) = b + M(a - b)~ $$ 对于所有 $a \in A$ 都成立。

　　 一旦选定某个点 $b$ 作为 “原点”，任何仿射映射都可以唯一地写成：一个平移，和一个以 $b$ 为中心的线性映射的组合。

5. 向量空间作为仿射空间

　　 每个向量空间 $V$ 都可以被看作自身上的仿射空间。这意味着：$V$ 的每个元素既可以看作点，也可以看作向量。这个仿射空间有时记作 $(V, V)$，以强调 $V$ 中元素的双重角色。当把零向量看作一个点时，常记为 $o$（或者大写 $O$，当点用大写字母表示时），并称为原点。

　　 如果 $A$ 是同一向量空间 $V$ 上的另一个仿射空间（即 $V = \overrightarrow{A}$），那么选择 $A$ 中的某个点 $a$ 可以定义一个唯一的仿射同构：这个同构在向量空间 $V$ 上是恒等映射；并把点 $a$ 映射为原点 $o$。换句话说，选择 $A$ 中的一个原点，就可以把仿射空间 $A$ 与 $(V, V)$ 在规范同构意义下视为相同。对应地，仿射空间 $A$ 也可以看作是向量空间 $V$ 的一个版本，只是 “原点的位置被遗忘了”。

6. 与欧几里得空间的关系

欧几里得空间的定义

　　 欧几里得空间（包括常见的一维直线、二维平面、三维空间，以及高维的类比空间）本质上都是仿射空间。

　　 在现代的多数定义中，欧几里得空间被定义为：一个仿射空间，其关联向量空间是一个有限维实内积空间，即一个带有正定二次型 $q(x)$ 的实数域向量空间。在这种定义下，两个向量 $x$ 和 $y$ 的内积通过如下对称双线性形式给出： $$ x \cdot y = \frac{1}{2} \big(q(x + y) - q(x) - q(y)\big)~ $$ 两个点 $A$ 和 $B$ 之间的欧几里得距离则是： $$ d(A, B) = \sqrt{q(B - A)}~ $$ 在较早的综合几何定义中：向量被定义为点对 $(A, B)$ 的等价类，等价关系是 “等势性”，即若点 $A, B, D, C$ 依次组成一个平行四边形，则 $(A, B)$ 与 $(C, D)$ 等价。在这种定义下：向量集合自然形成一个向量空间；欧几里得距离的平方构成这个向量空间上的一个二次型。可以直接验证，这种几何定义与现代的代数定义是等价的。

仿射性质

　　 在欧几里得几何中，常说的 “仿射性质” 是指一种可以在仿射空间中证明的性质，也就是说，这类性质不依赖于二次型或其对应的内积。

　　 换句话说，仿射性质是不涉及长度和角度的性质。典型示例：平行关系、切线的定义。 非示例：法线的定义，因为它依赖于角度的概念。等价地说，仿射性质就是在欧几里得空间中对所有仿射变换保持不变的性质。

7. 仿射组合与重心

　　 设 $a_1, a_2, \ldots, a_n$ 是仿射空间中的 $n$ 个点，$\lambda_1, \lambda_2, \ldots, \lambda_n$ 是底域中的 $n$ 个元素。

　　 1. 系数和为 0 的情况

　　 若：$\lambda_1 + \cdots + \lambda_n = 0$，则对任意两点 $o$ 和 $o'$，有： $$ \lambda_1 \overrightarrow{oa_1} + \cdots + \lambda_n \overrightarrow{oa_n} = \lambda_1 \overrightarrow{o'a_1} + \cdots + \lambda_n \overrightarrow{o'a_n}~ $$ 这说明这个向量的和与原点的选择无关，因此可以记为： $$ \lambda_1 a_1 + \cdots + \lambda_n a_n~ $$ 当：$n = 2$，$\lambda_1 = 1$、$\lambda_2 = -1$ 时，就得到了点的减法定义。

　　 2. 系数和为 1 的情况

　　 若：$\lambda_1 + \cdots + \lambda_n = 1$，选择一个原点 $o$，定义点 $g$ 使得： $$ \lambda_1 \overrightarrow{oa_1} + \cdots + \lambda_n \overrightarrow{oa_n} = \overrightarrow{og}~ $$ 可以证明，点 $g$ 的位置与原点的选择无关。因此： $$ g = \lambda_1 a_1 + \cdots + \lambda_n a_n~ $$ 这个点 $g$ 称为：点集 $\{a_i\}$ 在权重 $\{\lambda_i\}$ 下的重心，也可以说 $g$ 是这些点的仿射组合，系数为 $\{\lambda_i\}$。

8. 示例

9. 仿射生成与基

　　 对于仿射空间 $A$ 的任意一个非空子集 $X$：存在一个包含 $X$ 的最小仿射子空，称为 $X$ 的仿射生成。它等于所有包含 $X$ 的仿射子空间的交集。它的方向等于所有包含 $X$ 的仿射子空间的方向的交集。

　　 仿射生成的描述，$X$ 的仿射生成是 $X$ 中各点的所有有限仿射组合的集合。它的方向是集合 $\{x - y \mid x, y \in X\}$ 的线性生成空间。如果选取一个特定点 $x_0 \in X$，则方向也可以表示为集合 $\{x - x_0 \mid x \in X\}$ 的线性生成空间。因此，也可以说：$X$ 生成了它的仿射生成，而 $X$ 是它仿射生成的生成集。

　　 仿射无关与仿射基，如果 $X$ 的任一真子集的仿射生成，都是 $X$ 的仿射生成的真子空间，那么集合 $X$ 称为仿射无关，或简称为无关。一个仿射基，也称为重心框架（参见下文 “重心坐标” 部分），是既生成空间又无关的集合，即最小生成集。

　　 维度与仿射基，仿射空间的维数等于其关联向量空间的维数。对于一个有限维数为 $n$ 的仿射空间：仿射基是一个含有 $n+1$ 个点的无关集；等价地，仿射基是一个含有 $n+1$ 个点的生成集。

　　 换句话说：$\{x_0, x_1, \ldots, x_n\}$ 是仿射空间的一个仿射基，当且仅当 $\{x_1 - x_0, x_2 - x_0, \ldots, x_n - x_0\}$ 是其关联向量空间的一组线性基。

10. 坐标

　　 在仿射空间上，可以定义两类密切相关的坐标系。

重心坐标

　　 设 $A$ 是一个定义在域 $k$ 上、维数为 $n$ 的仿射空间，且 $\{x_0, x_1, \dots, x_n\}$ 是 $A$ 的一个仿射基。仿射基的性质意味着，对于 $A$ 中的任意一点 $x$，都存在唯一的一个 $(n+1)$-元组 $(\lambda_0, \lambda_1, \dots, \lambda_n)$，其元素属于域 $k$，并满足： $$ \lambda_0 + \lambda_1 + \cdots + \lambda_n = 1~ $$ 以及 $$ x = \lambda_0 x_0 + \lambda_1 x_1 + \cdots + \lambda_n x_n.~ $$ 这些 $\lambda_i$ 被称为点 $x$ 相对于仿射基 $\{x_0, x_1, \dots, x_n\}$ 的重心坐标。如果把各个 $x_i$ 看作具有 “重量”（或质量 $\lambda_i$ 的质点，那么点 $x$ 就是这些质点的重心。这也正是 “重心坐标” 这一术语的来源。

　　 重心坐标定义了仿射空间 $A$ 与 $k^{n+1}$ 中由方程 $\lambda_0 + \lambda_1 + \cdots + \lambda_n = 1$ 所确定的仿射子空间之间的一个仿射同构。

　　 对于无限维仿射空间，同样的定义依然适用，但仅使用有限和。这意味着对于每一个点，只有有限个坐标是非零的。

仿射坐标

　　 仿射标架是仿射空间中的一种坐标标架，由一个称为原点的点和该仿射空间所对应向量空间的一个线性基组成。更准确地说，对于一个仿射空间 $A$ 及其对应的向量空间 $\overrightarrow{A}$，原点 $o$ 属于 $A$，而线性基 $(v_1, v_2, \dots, v_n)$ 是 $\overrightarrow{A}$ 的一组基。（为简化符号，这里只讨论有限维的情况，无限维情形类似。）对于仿射空间 $A$ 中的每一个点 $p$，都存在唯一的一组来自底域的数 $\lambda_1, \lambda_2, \dots, \lambda_n$，使得： $$ p = o + \lambda_1 v_1 + \cdots + \lambda_n v_n,~ $$ 或等价地： $$ \overrightarrow{op} = \lambda_1 v_1 + \cdots + \lambda_n v_n.~ $$ 这些 $\lambda_i$ 就称为点 $p$ 相对于仿射标架 $(o, v_1, v_2, \dots, v_n)$ 的仿射坐标。

　　 例子：在欧几里得几何中，笛卡尔坐标就是相对于正交归一标架的仿射坐标。也就是说，这个仿射标架 $(o, v_1, \dots, v_n)$ 中，$(v_1, \dots, v_n)$ 构成一组正交归一基。

重心坐标与仿射坐标的关系

　　 重心坐标与仿射坐标密切相关，可以视为等价的表示方式。

　　 事实上，给定一个重心标架： $$ (x_0, x_1, \dots, x_n),~ $$ 可以直接推导出对应的仿射标架： $$ (x_0, \overrightarrow{x_0x_1}, \dots, \overrightarrow{x_0x_n}) = (x_0, x_1 - x_0, \dots, x_n - x_0)~ $$ 如果某个点相对于该重心标架的重心坐标为： $$ (\lambda_0, \lambda_1, \dots, \lambda_n),~ $$ 那么，该点相对于上述仿射标架的仿射坐标就是： $$ (\lambda_1, \dots, \lambda_n)~ $$ 反之，如果有一个仿射标架： $$ (o, v_1, v_2, \dots, v_n),~ $$ 那么： $$ (o,\, o+v_1,\, o+v_2,\, \dots,\, o+v_n)~ $$ 就是一个重心标架。

　　 如果某点相对于该仿射标架的仿射坐标为： $$ (\lambda_1, \lambda_2, \dots, \lambda_n),~ $$ 那么它相对于上述重心标架的重心坐标就是： $$ (1 - \lambda_1 - \cdots - \lambda_n,\, \lambda_1,\, \dots,\, \lambda_n)~ $$ 因此，重心坐标和仿射坐标几乎是等价的。不过，在大多数应用中，更倾向于使用仿射坐标，因为它涉及的独立坐标数量更少。然而，在某些问题中，如果关键点是仿射无关的，使用重心坐标有时能使计算更为简洁，下例就说明了这一点。

　　 三角形的例子

　　 一个非退化三角形的顶点构成了欧几里得平面中的一个仿射基。利用重心坐标，可以方便地描述三角形中许多与角度或距离无关的元素：顶点：重心坐标为 $(1, 0, 0)$、$(0, 1, 0)$ 和 $(0, 0, 1)$ 的点。边所在的直线：重心坐标中有一个坐标为零的所有点。边：重心坐标中有一个坐标为零，另外两个坐标为非负数的点。三角形的内部：所有坐标都为正数的点。中线：有两个坐标相等的点。重心：重心坐标为 $\left(\tfrac{1}{3}, \tfrac{1}{3}, \tfrac{1}{3}\right)$ 的点。

坐标变换

　　 重心坐标的情况

　　 重心坐标可以很方便地从一个基变换到另一个基。设 $\{x_0, x_1, \dots, x_n\}$ 和 $\{x'_0, x'_1, \dots, x'_n\}$ 是仿射空间 $A$ 的两组仿射基。对于 $A$ 中的任意一点 $x$，存在某个数列 $\{\lambda_0, \lambda_1, \dots, \lambda_n\}$，使得： $$ x = \lambda_0 x_0 + \lambda_1 x_1 + \cdots + \lambda_n x_n.~ $$ 同样，对于第一组基中的每一个基点 $x_i \in \{x_0, x_1, \dots, x_n\}$，在第二组基下可以表示为： $$ x_i = \lambda_{i,0} x'_0 + \cdots + \lambda_{i,j} x'_j + \cdots + \lambda_{i,n} x'_n,~ $$ 其中 $\{\lambda_{i,0}, \lambda_{i,1}, \dots, \lambda_{i,n}\}$ 是某个对应的系数序列。将第一组基下的表达式改写为第二组基下的形式，可以得到： $$ \begin{aligned} x &= \sum_{i=0}^n \lambda_i x_i \\[6pt] &= \sum_{i=0}^n \lambda_i \sum_{j=0}^n \lambda_{i,j} x'_j \\[6pt] &= \sum_{j=0}^n \left( \sum_{i=0}^n \lambda_i \lambda_{i,j} \right) x'_j. \end{aligned}~ $$ 因此，在第二组基下，点 $x$ 的重心坐标为：$\left\{\sum_i \lambda_i \lambda_{i,0},\;\sum_i \lambda_i \lambda_{i,1},\;\dots,\; \sum_i \lambda_i \lambda_{i,n}\right\}$ 这就给出了从第一组基到第二组基的重心坐标转换公式。

　　 仿射坐标的情况

　　 仿射坐标也可以方便地从一个基变换到另一个基。设 $o, \{v_1, v_2, \dots, v_n\}$ 和 $o', \{v'_1, v'_2, \dots, v'_n\}$ 是仿射空间 $A$ 的两组仿射标架。对于 $A$ 中的任意一点 $p$，存在唯一的一组来自底域的数列 $\lambda_1, \lambda_2, \dots, \lambda_n$，使得： $$ p = o + \lambda_1 v_1 + \cdots + \lambda_n v_n.~ $$ 同样，对于第一组标架中的基点，在第二组标架下可以表示为：

　　 原点 $o$： $$ o = o' + \lambda_{o,1} v'_1 + \cdots + \lambda_{o,j} v'_j + \cdots + \lambda_{o,n} v'_n,~ $$ 每个基向量 $v_i$： $$ v_i = \lambda_{i,1} v'_1 + \cdots + \lambda_{i,j} v'_j + \cdots + \lambda_{i,n} v'_n,~ $$ 其中，$\{\lambda_{o,1}, \dots, \lambda_{o,n}\}$ 和 $\{\lambda_{i,1}, \dots, \lambda_{i,n}\}$ 是相应的系数元组。将 $p$ 在第一组标架中的表达式改写为第二组标架下的表达式： $$ \begin{aligned} p &= o + \sum_{i=1}^{n} \lambda_i v_i \\ &= \left(o' + \sum_{j=1}^{n} \lambda_{o,j} v'_j\right) + \sum_{i=1}^{n} \lambda_i \sum_{j=1}^{n} \lambda_{i,j} v'_j\\ &= o' + \sum_{j=1}^{n} \left(\lambda_{o,j} + \sum_{i=1}^{n} \lambda_i \lambda_{i,j}\right) v'_j \end{aligned}~ $$ 因此，在第二组标架下，点 $p$ 的仿射坐标为： $$ \left\{\lambda_{o,1} + \sum_i \lambda_i \lambda_{i,1},\;\lambda_{o,2} + \sum_i \lambda_i \lambda_{i,2},\;\dots,\;\lambda_{o,n} + \sum_i \lambda_i \lambda_{i,n} \right\}~ $$ 这就给出了从第一组仿射标架到第二组仿射标架的坐标变换公式。

11. 仿射同态的性质

12. = 矩阵表示 =

　　 一个仿射变换 $T$ 在三维实射影空间 $\mathbb{P}^3(\mathbb{R}^3)$ 中通过一个具有特殊第四列的 $4 \times 4$ 矩阵实现： $$ A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & 0 \\ a_{21} & a_{22} & a_{23} & 0 \\ a_{31} & a_{32} & a_{33} & 0 \\ a_{41} & a_{42} & a_{43} & 1 \end{bmatrix} = \begin{bmatrix} T(1,0,0) & 0 \\ T(0,1,0) & 0 \\ T(0,0,1) & 0 \\ T(0,0,0) & 1 \end{bmatrix}~ $$ 该变换之所以是仿射而不是线性，是因为它包含了点 $(0,0,0)$；该点的变换结果揭示了仿射变换中的平移分量。

像与纤维

　　 设 $$ f: E \to F~ $$ 是一个仿射同态，其对应的线性映射为 $$ \vec{f}: \vec{E} \to \vec{F}.~ $$ 映射 $f$ 的像是 $F$ 的一个仿射子空间：$f(E) = \{ f(a) \mid a \in E \}$,其对应的向量空间是 $\vec{f}(\vec{E})$.由于仿射空间没有零元素，仿射同态没有核。然而，线性映射 $\vec{f}$ 是有核的。若记其核为 $K = \{ v \in \vec{E} \mid \vec{f}(v) = 0 \}$,那么，对于 $f(E)$ 中的任意一点 $x$，它的逆像 $ f^{-1}(x)$ 是 $E$ 的一个仿射子空间，其方向就是 $K$.这个仿射子空间称为 $x$ 的纤维。

投影

　　 一个重要的例子是**沿某一方向平行投影到某个仿射子空间**。这个例子之所以重要，在于欧几里得空间本质上是仿射空间，而这种类型的投影在欧几里得几何中具有基础性的意义。

　　 更具体地，设仿射空间 $E$ 的关联向量空间为 $\vec{E}$,令 $F$ 为一个方向为 $\vec{F}$ 的仿射子空间，同时令 $D$ 为 $\vec{E}$ 中 $\vec{F}$ 的一个补空间（即 $\vec{E}$ 中的每个向量都可以唯一地分解为一个属于 $\vec{F}$ 的向量和一个属于 $D$ 的向量之和）。对于 $E$ 中的每一点 $x$，它沿 $D$ 平行投影到 $F$ 的点 $p(x)$ 是 $F$ 中唯一满足 $$ p(x) - x \in D~ $$ 的点。这个投影 $p$ 是一个仿射同态，其对应的线性映射 $\vec{p}$ 定义为： $$ \vec{p}(x - y) = p(x) - p(y)~ $$ 其中 $x, y \in E$。

　　 该投影的像是子空间 $F$，而它的纤维是方向为 $D$ 的子空间。

商空间

　　 尽管仿射空间没有核的定义，但商空间是可以定义的。这是因为 “属于仿射同态的同一纤维” 构成了一个等价关系。

　　 设 $E$ 是一个仿射空间，$D$ 是其关联向量空间 $\vec{E}$ 中的一个线性子空间。则 $E$ 关于 $D$ 的商空间 $E / D$ 是指根据以下等价关系定义的商集：若 $$ x - y \in D,~ $$ 则 $x$ 与 $y$ 等价。

　　 该商空间 $E / D$ 本身是一个仿射空间，其关联向量空间是 $\vec{E} / D.$

　　 对于任意一个仿射同态 $E \to F$.其像与 $E$ 关于其对应线性映射的核的商空间同构。这就仿射空间的第一同构定理。

13. 公理

　　 仿射空间通常通过解析几何结合坐标或等价的向量空间方法来研究。但它们也可以通过综合几何的方式，用公理化体系来描述，尽管这种方法并不常见。对于仿射空间，有多种不同的公理体系。

　　 Coxeter（1969，第 192 页）将实数范围内的仿射几何作为一个特殊情形加以公理化，定义为：有序几何+ 仿射形式的德萨格定理+ 一个平面公理，即 “在平面中，给定一条直线和直线外的一点，最多只能有一条通过该点且不与该直线相交的直线”。

　　 仿射平面满足以下公理（Cameron 1991，第 2 章）：（其中，若两条直线相等或互不相交，则称它们平行）

　　 除了定义在域（或除环）上的仿射平面之外，还有许多非德萨格平面也满足这些公理。Cameron（1991，第 3 章）还给出了高维仿射空间的公理体系。

　　 纯粹公理化的仿射几何比仿射空间的概念更一般，相关内容详见 “仿射几何” 条目。

14. 与射影空间的关系

图
图 3

　　 仿射空间可以看作包含在射影空间中。例如，一个仿射平面可以通过从任意射影平面中移除一条直线及其上的所有点而获得；反之，任何仿射平面也可以通过添加一条 “无穷远直线” 来构造其闭包形式的射影平面，这条无穷远直线上的点对应于仿射平面中平行直线的等价类。在更高维空间中，也存在类似的构造方法。

　　 此外，射影空间中的某些变换若能保持仿射空间（等价于保持无穷远超平面作为一个整体不变），就会导出仿射空间上的变换。反之，任何仿射线性变换都可以唯一地扩展为一个射影线性变换，因此仿射群是射影群的一个子群。

　　 例如，莫比乌斯变换（即复射影直线或黎曼球面上的变换）在且仅在保持无穷远点不变时，才是复平面上的仿射变换。

15. 仿射代数几何

　　 在代数几何中，仿射簇（affine variety，或更一般的仿射代数集 affine algebraic set）定义为仿射空间中的一个子集，它由一组所谓的多项式函数在该仿射空间上的公共零点集构成。

　　 为了在仿射空间上定义多项式函数，需要先选定一个仿射参考系。在这种参考系下，多项式函数指的是这样一种函数：其在任意一点的值等于该点坐标的某个多元多项式的值。由于仿射坐标的变换可以通过坐标的线性（更准确地说是仿射）函数来表示，因此该定义不依赖于具体的坐标选择。

　　 在一个定义于域 $k$ 上、维数为 $n$ 的仿射空间 $\mathbb{A}_k^n$ 中，选择一组仿射坐标系会在 $\mathbb{A}_k^n$ 与仿射坐标空间 $k^n$ 之间建立一个仿射同构。这也解释了为什么许多教材为了简化记号，会写作 $\mathbb{A}_k^n = k^n$ 并将仿射代数簇定义为 $k^n$ 上多项式函数的公共零点集。[9]

　　 由于整个仿射空间本身就是零多项式的公共零点集，所以仿射空间本身也是一个仿射代数簇。

多项式函数环

　　 根据前述定义，选择仿射空间 $\mathbb{A}_k^n$ 的一个仿射参考系，可以将 $\mathbb{A}_k^n$ 上的多项式函数与 n 个变量的多项式对应起来，其中第 $i$ 个变量表示将一个点映射到其第 $i$ 个坐标的函数。因此，$\mathbb{A}_k^n$ 上的多项式函数集合形成一个 $k$-代数，记为 $k[\mathbb{A}_k^n],$ 它与多项式环 $k[X_1, X_2, \dots, X_n]$ 同构。

　　 当坐标系发生变化时，$k[\mathbb{A}_k^n]$ 与 $k[X_1, X_2, \dots, X_n]$ 之间的同构关系也会随之变化，这会在多项式环 $k[X_1, X_2, \dots, X_n]$ 上诱导出一个自同构，该自同构会把每个不定元映射到一个一次多项式。由此可以推出：总次数定义了 $k[\mathbb{A}_k^n]$ 的一个滤子（，并且这个滤子与坐标系的选择无关；总次数也定义了一个分次，但这个分次会依赖于坐标选择，因为仿射坐标的改变可能会把不定元映射为非齐次多项式。

Zariski 拓扑

　　 定义在拓扑域（如实数域或复数域）上的仿射空间具有自然拓扑。而 Zariski 拓扑则是在任意域上的仿射空间中定义的一种拓扑，它使得无论底层域是什么，都可以使用拓扑方法进行研究。

　　 Zariski 拓扑是仿射空间上的一种唯一拓扑，其闭集定义为仿射代数集（即多项式函数在仿射空间上的公共零点集）。在拓扑域上，由于多项式函数都是连续的，因此每个 Zariski 闭集在自然拓扑下也是闭集。换句话说，在拓扑域上，Zariski 拓扑比自然拓扑更粗糙。

　　 此外，存在一个从仿射空间到其多项式函数环的素理想集（即谱，spectrum）的自然单射。当选定仿射坐标后，这个映射会把坐标为 $(a_1, a_2, \dots, a_n)$ 的点映射到多项式环中的极大理想 $\langle X_1 - a_1, X_2 - a_2, \dots, X_n - a_n \rangle$。该映射是一个同胚（在仿射空间的 Zariski 拓扑与多项式函数环谱的 Zariski 拓扑之间）onto 其像。

　　 当底域是代数闭域时，这个性质在代数几何中尤为重要，因为此时上面的同胚恰好是仿射空间与其函数环所有极大理想集之间的对应关系。这正是 Hilbert 零点定理的体现。

　　 这也是 Grothendieck 模式理论的起点。在模式理论中，为了研究代数簇，不仅把仿射空间中的点作为 “点”，还将谱中的所有素理想也视为 “点”。这样做允许像拼接流形图册构造流形那样，将局部的代数簇拼接起来，从而构建更复杂的代数几何对象。

上同调

　　 与所有仿射簇一样，仿射空间上的局部数据总能拼接为全局数据：仿射空间的上同调是平凡的。更精确地说，对于所有相干层 $\mathbf{F}$ 和所有整数 $i > 0$，$H^i\left(\mathbb{A}_k^n, \mathbf{F}\right) = 0$。这一性质同样适用于所有其他仿射簇（参见 Serre 仿射性定理）。此外，仿射空间上的所有étale 上同调群也都是平凡的。特别地，每一个线丛都是平凡的。更一般地，Quillen–Suslin 定理表明：仿射空间上的每一个代数向量丛都是平凡的。

16. 参见

17. 注释

  1. “translation” 一词通常优于 “displacement vector”，因为后者容易引起误解，“displacement” 有时还包含旋转的含义。
  2. Berger 1987，第 32 页
  3. Berger, Marcel (1984), “Affine spaces”, Problems in Geometry, Springer, 第 11 页, ISBN 9780387909714
  4. Berger 1987，第 33 页
  5. Snapper, Ernst; Troyer, Robert J. (1989), Metric Affine Geometry, 第 6 页
  6. Tarrida, Agusti R. (2011), “Affine spaces”, Affine Maps, Euclidean Motions and Quadrics, Springer, 第 1–2 页, ISBN 9780857297105
  7. Nomizu & Sasaki 1994，第 7 页
  8. Strang, Gilbert (2009). Introduction to Linear Algebra (第 4 版). Wellesley: Wellesley-Cambridge Press. 第 460 页. ISBN 978-0-9802327-1-4
  9. Hartshorne 1977, 第 I 章，第 1 节

18. 参考文献


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利