巴拿赫-塔斯基定理（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：“一个球是否可以被分解为有限个点集，并重新组合成两个与原球相同的球？”

　　 巴拿赫–塔尔斯基悖论是集合论几何中的一个定理，其内容如下：给定三维空间中的一个实心球体，存在一种将该球体分解为有限个不相交子集的方式，这些子集可以以不同的方式重新组合，从而得到两个与原球体完全相同的副本。实际上，重新组合过程仅涉及移动和旋转这些部分，而不改变它们的原始形状。然而，这些部分本身并不是传统意义上的 “固体”，而是无穷多个点的散布。重构可以通过最少五个部分来实现。\(^\text{[1]}\)

　　 定理的另一种形式表述为：给定任意两个 “合理的” 固体物体（例如一个小球和一个巨大球），这两个物体的切割部分可以重新组合成对方。这通常被非正式地表述为 “一个豌豆可以被切割并重新组合成太阳”，并被称为“豌豆和太阳悖论”。

　　 该定理是一个真实悖论：它与基本的几何直觉相矛盾，但并不是错误的或自相矛盾的。通过将球体分割成部分并通过旋转和平移来移动它们，而没有任何拉伸、弯曲或添加新点，“将球体翻倍” 似乎是不可能的，因为所有这些操作从直觉上讲都应该保持体积不变。这样的操作保持体积的直觉并不是数学上荒谬的，甚至它也包含在体积的正式定义中。然而，这里不适用这种直觉，因为在这种情况下，无法定义所考虑子集的体积。重新组合它们会产生一个具有体积的集合，而这个体积恰好与开始时的体积不同。

　　 与大多数几何定理不同，这个结果的数学证明在关键的方面依赖于集合论公理的选择。它可以通过选择公理来证明，该公理允许构造不可测量的集合，即没有普通意义上体积的点集，而其构造需要不可数次的选择。\(^\text{[2]}\)

　　 2005 年曾证明，分解中的各个部分可以以一种方式选择，使它们可以连续地移动到适当的位置，而不会相互碰撞。\(^\text{[3]}\)

　　 正如 Leroy\(^\text{[4]}\) 和 Simpson\(^\text{[5]}\) 独立证明的那样，Banach–Tarski 悖论在使用局部空间而不是拓扑空间时不会违反体积。在这种抽象的设置中，可能存在没有点但仍然非空的子空间。悖论分解的部分在局部空间的意义上相互交叠得很厉害，以至于这些交集中的一些应该被赋予正的质量。允许将这种隐藏的质量考虑在内，局部空间理论使得欧几里得空间的所有子集（甚至所有子局部空间）都能得到令人满意的度量。

1. Banach 和 Tarski 的论文

　　 在 1924 年发表的一篇论文中，\(^\text{[6]}\) 斯特凡·巴拿赫和阿尔弗雷德·塔尔斯基给出了一个这种悖论分解的构造，基于朱塞佩·维塔利关于单位区间的早期工作，以及费利克斯·豪斯多夫对球体的悖论分解，并讨论了与欧几里得空间中各种维度的子集分解相关的若干问题。他们证明了以下更一般的命题，即 Banach-Tarski 悖论的强形式：

　　 给定任何两个欧几里得空间中至少三维的有界子集 \( A \) 和 \( B \)，且这两个子集都有非空的内部，则 \( A \) 和 \( B \) 可以被分解成有限个不相交的子集，\(A = A_1 \cup \cdots \cup A_k\),\(B = B_1 \cup \cdots \cup B_k \)(其中 \(k\) 为某个整数)，使得对于每一个 \( i \)（\( i \) 在 1 到 \( k \) 之间的整数），集合 \( A_i \) 和 \( B_i \) 是全等的。

　　 现在让 \( A \) 为原始的球体，\( B \) 为原始球体的两个平移副本的并集。则这一命题的意思是，原始的球体 \( A \) 可以被分割成若干个部分，然后通过旋转和平移，使得结果是包含两个 \( A \) 副本的整个集合 \( B \)。

　　 Banach-Tarski 悖论的强形式在一维和二维中是错误的，但巴拿赫和塔尔斯基表明，如果允许可数多个子集，类似的命题仍然成立。维度 1 和 2 与 3 及更高维度之间的差异，源于三维欧几里得运动群 \( E(n) \) 的更丰富结构。对于 \( n = 1, 2 \)，该群是可解的，但对于 \( n \geq 3 \)，它包含一个有两个生成元的自由群。约翰·冯·诺依曼研究了使得悖论分解成为可能的等价群的性质，并引入了可容许群的概念。他还在平面中发现了一个悖论的形式，使用保持面积的仿射变换代替通常的全等变换。

　　 塔尔斯基证明了可容许群恰好是那些不存在悖论分解的群。由于在巴拿赫-塔尔斯基悖论中只需要自由子群，这导致了长期存在的冯·诺依曼猜想，该猜想在 1980 年被反驳。

2. 形式处理

　　 巴拿赫-塔尔斯基悖论指出，普通欧几里得空间中的一个球体可以通过仅使用将其分割成子集、用全等的集合替换一个集合以及重新组合的操作来 “翻倍”。其数学结构通过强调欧几里得运动群的作用以及引入等分解集合和悖论集合的概念得到了极大阐明。假设 \( G \) 是一个作用于集合 \( X \) 的群。在最重要的特例中，\( X \) 是一个 \( n \)-维欧几里得空间（对于整数 \( n \)），而 \( G \) 由所有 \( X \) 的等距变换组成，即保持距离的 \( X \) 到自身的变换，通常表示为 \( E(n) \)。两个几何图形如果可以相互转换，则称它们是全等的，这一术语将扩展到一般的 \( G \)-作用。若集合 \( A \) 和 \( B \) 可以被分割成相同个数的、分别与 \( G \) 全等的部分，则称 \( A \) 和 \( B \) 是 \( G \)-等分解的，或称与 \( G \) 相对于等分解。这个定义了 \( X \) 中所有子集之间的一个等价关系。正式地，如果存在非空集合 \(A_1, \dots, A_k, \quad B_1, \dots, B_k\) 使得 \[ A = \bigcup _{i=1}^{k}A_{i}, \quad B = \bigcup _{i=1}^{k}B_{i},~ \] \[ A_i \cap A_j = B_i \cap B_j = \emptyset \quad \text{for all } 1 \leq i < j \leq k,~ \] 并且存在元素 \( g_i \in G \) 使得 \[ g_i(A_i) = B_i \quad \text{for all } 1 \leq i \leq k,~ \] 则可以说 \( A \) 和 \( B \) 是用 \( k \) 个部分 \( G \)-等分解的。如果集合 \( E \) 有两个不相交的子集 \( A \) 和 \( B \)，使得 \( A \) 和 \( E \)，以及 \( B \) 和 \( E \) 都是 \( G \)-等分解的，则称 \( E \) 是悖论的。

　　 使用这些术语，巴拿赫-塔尔斯基悖论可以重新表述为：

　　 三维欧几里得球体与其两个副本是等分解的。 事实上，由 Raphael M. Robinson 提出了一个明确的结果：\(^\text{[7]}\) 将球体翻倍可以用五个部分完成，而少于五个部分将不足以完成。

　　 巴拿赫-塔尔斯基悖论可以通过指出，在悖论的强形式中，对于两个集合，总是存在一个双射函数，可以将一个形状中的点一对一地映射到另一个形状中。在乔治·坎托尔集合论的语言中，这两个集合具有相同的基数。因此，如果将群扩展以允许 \( X \) 的任意双射，那么所有具有非空内部的集合都会变得全等。同样，一个球体可以通过拉伸变成更大或更小的球体，换句话说，通过应用相似变换。因此，如果群 \( G \) 足够大，就可以找到一些 \( G \)-等分解的集合，它们的 “大小” 各不相同。此外，由于可数集合可以变成其两个副本，因此可以预期，使用可数多个部分可能以某种方式完成这一操作。

　　 另一方面，在巴拿赫-塔尔斯基悖论中，分割的部分是有限的，且允许的等价变换是欧几里得全等变换，这些变换保持体积。然而，尽管如此，它们最终还是能够将球体的体积翻倍。虽然这无疑令人惊讶，但在悖论分解中使用的一些部分是不可测集，因此它们的体积（更准确地说是勒贝格测度）并未定义，因此这种分割无法以实际的方式完成。事实上，巴拿赫-塔尔斯基悖论表明，在三维及更高维的欧几里得空间的所有子集上，无法找到一个有限可加的测度（或 Banach 测度），该测度对欧几里得运动是不变的，并且在单位立方体上取值为 1。在他的后期工作中，塔尔斯基证明了，反过来，这种类型的悖论分解的不存在意味着存在一个有限可加的不变测度。

　　 下面给出的 “翻倍球体” 形式悖论的证明核心是一个显著的事实：通过一个欧几里得等距变换（并重新命名元素），可以将一个特定的集合（本质上是单位球面）分成四部分，然后将其中一部分旋转，使其变成它本身加上其他两个部分。这可以从 \(F_2\) 群的 \(F_2\) 悖论分解中相对容易地得到，\(F_2\) 是一个有两个生成元的自由群。Banach 和 Tarski 的证明依赖于豪斯多夫几年前发现的一个类似事实：空间中单位球体的表面是三个集合 \( B \)，\( C \)，\( D \) 和一个可数集 \( E \) 的不相交并集，其中，\( B \)，\( C \)，\( D \) 成对全等，另一方面，\( B \) 与 \( C \) 和 \( D \) 的并集全等。这通常被称为 豪斯多夫悖论。

与早期工作的联系及选择公理的作用

　　 Banach 和 Tarski 明确承认，朱塞佩·维塔利在 1905 年构造的以他名字命名的集合、豪斯多夫的悖论（1914），以及巴拿赫在 1923 年的早期论文，是他们工作的先驱。维塔利和豪斯多夫的构造依赖于采尔梅洛的选择公理（“AC”），该公理在 Banach-Tarski 论文中同样至关重要，既用于证明他们的悖论，也用于证明另一个结果：

　　 两个欧几里得多边形，其中一个严格包含另一个，是不可等分解的。

　　 他们指出：

　　 Le rôle que joue cet axiome dans nos raisonnements nous semble mériter l'attention （这个公理在我们推理中所起的作用似乎值得关注）

　　 他们指出，虽然第二个结果完全符合几何直觉，但其证明比悖论的证明更为依赖选择公理（AC）。因此，Banach 和 Tarski 暗示，选择公理不应仅仅因为它产生了悖论分解而被拒绝，因为这样的论点也会破坏几何直觉性陈述的证明。

　　 然而，在 1949 年，A. P. Morse 表明，关于欧几里得多边形的陈述可以在 ZF 集合论中证明，因此不需要选择公理。\(^\text{[8]}\) 在 1964 年，保罗·科恩证明了选择公理与 ZF 独立——也就是说，选择公理不能从 ZF 中证明。\(^\text{[9]}\) 选择公理的一个较弱版本是依赖选择公理（dependent choice，DC），并且已经证明，DC 不能证明巴拿赫-塔尔斯基悖论，即：

　　 巴拿赫-塔尔斯基悖论不是 ZF 或 ZF+DC 的定理，假设它们的一致性。\(^\text{[10]}\)

　　 大量的数学研究依赖于选择公理。正如斯坦·瓦根在其专著的最后指出的那样，巴拿赫-塔尔斯基悖论对于纯数学的作用比对于基础问题更为重要：它激发了一个富有成果的新研究方向——群的可容许性，这与基础问题无关。

　　 在 1991 年，利用当时由马修·福尔曼和弗里德里希·韦伦的最新结果，\(^\text{[11]}\) 雅努什·帕夫利科夫斯基证明了巴拿赫-塔尔斯基悖论可以从 ZF 加上哈恩-巴拿赫定理推出。\(^\text{[12]}\) 哈恩-巴拿赫定理不依赖于完整的选择公理，但可以使用选择公理的一个较弱版本——超滤子引理来证明。

3. 证明的概述

　　 这里给出了一个与 Banach 和 Tarski 所给证明相似但不完全相同的证明概述。本质上，球体的悖论分解通过以下四个步骤实现：

  1. 找到两个生成元的自由群的悖论分解。
  2. 找到一个在三维空间中的旋转群，该群同构于两个生成元的自由群。
  3. 利用该群的悖论分解和选择公理，生成空心单位球的悖论分解。
  4. 将球体的分解扩展到实心单位球的分解。

　　 下面将更详细地讨论这些步骤。

步骤 1

图
图 2：\( F_2 \) 的 Cayley 图，显示了对集合 \( S(a) \) 和 \( aS(a^{-1}) \) 的分解。沿着图中水平边缘向右行进表示将 \( F_2 \) 的一个元素左乘以 \( a \)；沿着图中垂直边缘向上行进表示将 \( F_2 \) 的一个元素左乘以 \( b \)。集合 \( S(a) \) 的元素是绿色点；集合 \( aS(a^{-1}) \) 的元素是蓝色点或带有蓝色边框的红色点。带有蓝色边框的红色点是集合 \( S(a^{-1}) \) 的元素，而 \( S(a^{-1}) \) 是 \( aS(a^{-1}) \) 的子集。

　　 由两个生成元 \( a \) 和 \( b \) 生成的自由群由所有可以从四个符号 \( a \)、\( a^{-1} \)、\( b \) 和 \( b^{-1} \) 组成的有限字符串构成，且其中不允许 \( a \) 紧邻 \( a^{-1} \)，也不允许 \( b \) 紧邻 \( b^{-1} \)。这样的字符串可以通过连接两个字符串并反复将 “禁止” 的子字符串替换为空字符串来转换为此类字符串。例如：将 \( abab^{-1}a^{-1} \) 与 \( abab^{-1}a \) 连接得到 \( abab^{-1}a^{-1}abab^{-1}a \)，其中包含子字符串 \( a^{-1}a \)，因此可以简化为 \( abab^{-1}bab^{-1}a \)，接着包含子字符串 \( b^{-1}b \)，再简化为 \( abaab^{-1}a \)。可以验证，这些字符串在这个操作下的集合构成一个群，单位元是空字符串 \( e \)。这个群可以称为 \( F_2 \)。

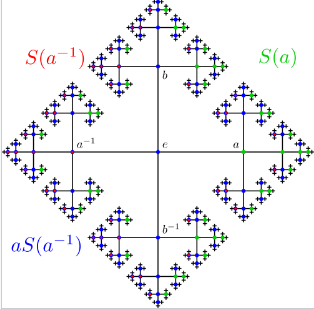
　　 群 \( F_2 \) 可以通过以下方式 “悖论性分解”：让 \( S(a) \) 是 \( F_2 \) 中由所有以 \( a \) 开头的字符串组成的子集，类似地定义 \( S(a^{-1}) \)、\( S(b) \) 和 \( S(b^{-1}) \)。显然， \[ F_2 = \{ e \} \cup S(a) \cup S(a^{-1}) \cup S(b) \cup S(b^{-1})~ \] 但同时， \[ F_2 = aS(a^{-1}) \cup S(a),~ \] 以及 \[ F_2 = bS(b^{-1}) \cup S(b),~ \] 其中符号 \( aS(a^{-1}) \) 表示将所有属于 \( S(a^{-1}) \) 的字符串与 \( a \) 连接在一起。

　　 这正是证明的核心。例如，在集合 \( aS(a^{-1}) \) 中，可能有一个字符串 \( aa^{-1}b \)，由于规则要求 \( a \) 不能出现在 \( a^{-1} \) 旁边，因此它简化为字符串 \( b \)。类似地，\( aS(a^{-1}) \) 包含所有以 \( a^{-1} \) 开头的字符串（例如，字符串 \( aa^{-1}a^{-1} \) 被简化为 \( a^{-1} \)）。通过这种方式，\( aS(a^{-1}) \) 包含所有以 \( b \)、\( b^{-1} \) 和 \( a^{-1} \) 开头的字符串，以及空字符串 \( e \)。

　　 群 \( F_2 \) 被切割成四个部分（加上单元素集合 \( \{e\} \)），然后通过与 \( a \) 或 \( b \) 相乘将其中两个 “移位”，再将它们 “重新组合” 成两个部分，一个部分形成 \( F_2 \) 的一个副本，另一个部分形成 \( F_2 \) 的另一个副本。这正是要对球体执行的操作。

步骤 2

　　 为了找到一个三维空间的自由旋转群，即一个与自由群 \( F_2 \) 行为相同（或 “同构”）的群，选择两个正交轴（例如，x 轴和 z 轴）。然后，令 \( A \) 是绕 x 轴旋转 \( \theta = \arccos \left( \frac{1}{3} \right) \) 的旋转，令 \( B \) 是绕 z 轴旋转 \( \theta \) 的旋转（这里也可以使用许多其他合适的无理倍数的 \( \pi \) 来替代）。\(^\text{[13]}\)

　　 由 \( A \) 和 \( B \) 生成的旋转群将被称为 \( H \)。令 \( \omega \) 为 \( H \) 中的一个元素，该元素从绕 z 轴的正向旋转开始，即一个形式为 \(\omega = \ldots b^{k_3} a^{k_2} b^{k_1}\) 的元素，其中 \(k_1 > 0,\ k_2, k_3, \ldots, k_n \neq 0,\ n \geq 1\). 可以通过归纳法证明，\( \omega \) 将点 \( (1, 0, 0) \) 映射到 \(\left( \frac{k}{3^N}, \frac{l \sqrt{2}}{3^N}, \frac{m}{3^N} \right)\) 对于某些 \( k, l, m \in \mathbb{Z} \)，\( N \in \mathbb{N} \)。通过对 \( k, l \) 和 \( m \) 取模 3 进行分析，可以证明 \( l \neq 0 \)。同样的论证（通过问题的对称性）在 \( \omega \) 从绕 z 轴的负向旋转或绕 x 轴的旋转开始时也成立。这表明，如果 \( \omega \) 由 \( A \) 和 \( B \) 中的非平凡词生成，那么 \( \omega \neq e \)。因此，群 \( H \) 是一个自由群，且与 \( F_2 \) 同构。

　　 这两个旋转的行为与群 \( F_2 \) 中的元素 \( a \) 和 \( b \) 完全相同：现在，群 \( H \) 具有悖论性分解。

　　 这个步骤无法在二维中执行，因为它涉及三维空间中的旋转。如果围绕同一轴进行两个非平凡的旋转，则得到的群要么是 \( \mathbb{Z} \)（如果两个角度之间的比值是有理数），要么是由两个元素生成的自由阿贝尔群；无论哪种情况，它都不具备步骤 1 中所要求的性质。

　　 使用积分四元数对某些特殊正交群中自由群存在性的替代算术证明，导致了旋转群的悖论性分解。\(^\text{[14]}\)

步骤 3

　　 单位球面 \( S^2 \) 被群 \( H \) 的作用分成了轨道：当且仅当存在群 \( H \) 中的一个旋转将第一个点移到第二个点时，两个点属于同一轨道。（注意，点的轨道是 \( S^2 \) 中的稠密集。）可以使用选择公理从每个轨道中选择一个点；将这些点收集成一个集合 \( M \)。群 \( H \) 对一个给定轨道的作用是自由的和传递的，因此每个轨道可以与 \( H \) 对应。换句话说，\( S^2 \) 中的每个点都可以通过应用群 \( H \) 中的适当旋转，将 \( M \) 中的适当元素映射到该点。由于这一点，群 \( H \) 的悖论性分解导致了 \( S^2 \) 的悖论性分解，将 \( S^2 \) 分成四个部分 \( A_1, A_2, A_3, A_4 \)，如下所示： \[ A_1 = S(a)M \cup M \cup B~ \] \[ A_2 = S(a^{-1})M \setminus B~ \] \[ A_3 = S(b)M~ \] \[ A_4 = S(b^{-1})M~ \] 其中我们定义 \[ S(a)M = \{ s(x) \mid s \in S(a), x \in M \}~ \] 对于其他集合同理，并且我们定义 \[ B = a^{-1}M \cup a^{-2}M \cup \dots~ \] （\( F_2 \) 的五个 “悖论” 部分没有被直接使用，因为它们在翻倍后会将 \( M \) 留作额外的一部分，这是由于单元素集合 \( \{e\} \) 的存在。）

　　 现在，球面的大部分已经被分成了四个集合（每个集合在球面上都是稠密的），当其中的两个集合旋转时，结果是原来所得到的结果的两倍： \[ aA_2 = A_2 \cup A_3 \cup A_4~ \] \[ bA_4 = A_1 \cup A_2 \cup A_4~ \]

步骤 4

　　 最后，将 \( S^2 \) 上的每个点与原点连接一个半开区间；然后，\( S^2 \) 的悖论性分解就会导致实心单位球的悖论性分解，去掉球心的点。（这个中心点需要更多的注意；见下文。）

　　 注意：这个概述省略了一些细节。必须小心那些恰好位于群 \( H \) 中某些旋转轴上的球面上的点。然而，这样的点只有可数多个，像球心的点一样，可以修补证明来考虑它们。（见下文。）

一些细节，补充说明

　　 在步骤 3 中，球面被分割成了我们群 \( H \) 的轨道。为了简化证明，省略了固定于某些旋转的点的讨论；由于 \( F_2 \) 的悖论性分解依赖于移动某些子集，因此某些点被固定可能会引起一些麻烦。由于 \( S^2 \) 的任何旋转（除了零旋转）都有恰好两个固定点，并且因为 \( H \) 是与 \( F_2 \) 同构的可数群，所以 \( S^2 \) 中有可数多个点是某个旋转在 \( H \) 中固定的。将这个固定点的集合记为 \( D \)。步骤 3 证明了 \( S^2 - D \) 存在悖论性分解。

　　 接下来需要证明的是以下命题：\( S^2 - D \) 与 \( S^2 \) 是等分解的。

　　 证明。令 \( \lambda \) 是通过原点的某条直线，并且不与 \( D \) 中的任何点相交。由于 \( D \) 是可数的，这是可能的。令 \( J \) 是角度集合 \( \alpha \)，使得对于某个自然数 \( n \) 和某个 \( P \in D \)，旋转 \( r(n\alpha)P \) 也在 \( D \) 中，其中 \( r(n\alpha) \) 是绕 \( \lambda \) 旋转 \( n\alpha \)。那么 \( J \) 是可数的。因此，存在一个角度 \( \theta\) 不在 \( J \) 中。令 \( \rho \) 是绕 \( \lambda \) 旋转 \( \theta \) 的旋转。然后，\( \rho \) 在 \( S^2 \) 上作用，没有在 \( D \) 中的固定点，即 \( \rho^n(D) \) 与 \( D \) 不相交，并且对于自然数 \( m < n \)，\( \rho^n(D) \) 与 \( \rho^m(D) \) 不相交。令 \( E \) 为 \( \rho^n(D) \) 的不相交并集，其中 \( n = 0, 1, 2, \dots \)。那么 \[ S^2 = E \cup (S^2 - E) \sim \rho(E) \cup (S^2 - E) = (E - D) \cup (S^2 - E) = S^2 - D,~ \] 其中 \( \sim \) 表示 “是等分解的”。

　　 对于步骤 4，已经证明了去掉一个点的球体存在悖论性分解；剩下要证明的是去掉一个点的球体与球体是等分解的。考虑球体内的一条圆，包含球体中心的点。通过类似于证明命题时所用的论证，可以看到完整的圆与去掉球体中心点的圆是等分解的。（基本上，圆上的可数个点可以通过旋转映射到自身加上一个点。）注意，这涉及绕原点以外的点旋转，因此巴拿赫-塔尔斯基悖论涉及的是欧几里得三维空间的等距变换，而不仅仅是 \( SO(3) \) 变换。

　　 利用以下事实：如果 \( A \sim B \) 且 \( B \sim C \)，则 \( A \sim C \)。将 \( A \) 分解为 \( C \) 可以使用的部分数等于将 \( A \) 转换为 \( B \) 所需部分数与将 \( B \) 转换为 \( C \) 所需部分数的乘积。

　　 上述证明需要 \( 2 \times 4 \times 2 + 8 = 24 \) 个部分——一个因子 2 用于去除固定点，一个因子 4 来自步骤 1，一个因子 2 用于重新创建固定点，另有 8 个用于第二个球体的中心点。但在步骤 1 中，当将 \( \{e\} \) 和所有形如 \( a^n \) 的字符串移动到 \( S(a^{-1}) \) 时，对除一个轨道之外的所有轨道执行此操作。将这个最后一个轨道的 \( \{e\} \) 移动到第二个球体的中心点。这将总数减少到 16 + 1 个部分。通过更多的代数运算，也可以将固定轨道分解为与步骤 1 中相同的 4 个集合。这会给出 5 个部分，这是最优解。

4. 从一个球体中获得无限多个球体

　　 利用 Banach-Tarski 悖论，可以从欧几里得 \( n \)-空间中的一个球体获得 \( k \) 个球体的副本，其中任意整数 \( n \geq 3 \) 和 \( k \geq 1 \)，即一个球体可以被切割成 \( k \) 个部分，使得每个部分都与原始球体大小相同的球体等分解。利用自由群 \( F_2 \)（秩为 2）承认一个可数无限秩的自由子群的事实，类似的证明可以得出单位球面 \( S^{n-1} \) 可以被分割成可数无限多个部分，每个部分都与 \( S^{n-1} \) 等分解（使用两个部分）。通过使用旋转群 \( SO(n) \) 的解析性质，\( SO(n) \) 是一个联通的解析李群，进一步可以证明，球面 \( S^{n-1} \) 可以被分割成与实数一样多的部分（即 \( 2^{\aleph_0} \) 个部分），使得每个部分与 \( S^{n-1} \) 使用两个部分旋转后等分解。这些结果随后可以推广到去掉原点的单位球体。2010 年瓦列里·楚尔金的一篇文章给出了巴拿赫-塔尔斯基悖论连续版本的新证明。\(^\text{[14]}\)

5. 冯·诺依曼悖论在欧几里得平面中的表现

　　 在欧几里得平面中，相对于欧几里得运动群等分解的两个图形必然具有相同的面积，因此，使用仅仅是欧几里得全等变换的 Banach-Tarski 类型的正方形或圆盘的悖论性分解是不可能的。约翰·冯·诺依曼给出了平面和更高维度情形之间区别的概念性解释：与三维中的旋转群 \( SO(3) \) 不同，欧几里得平面上的运动群 \( E(2) \) 是可解的，这意味着在 \( E(2) \) 和 \( \mathbb{R}^2 \) 上存在一个有限可加的测度，该测度在平移和旋转下是不变的，从而排除了非忽略集合的悖论性分解。冯·诺依曼随后提出了以下问题：如果允许更大的等价群，这样的悖论性分解是否可以构造？

　　 显然，如果允许相似变换，那么平面中的任何两个正方形即使没有进一步细分，也会变得等价。这促使我们将注意力限制在保持面积的仿射变换群 \( SA_2 \) 上。由于面积保持不变，任何关于这个群的正方形的悖论性分解将由于与巴拿赫-塔尔斯基悖论性分解相同的原因而显得反直觉。事实上，群 \( SA_2 \) 包含特殊线性群 \( SL(2, \mathbb{R}) \) 作为一个子群，而 \( SL(2, \mathbb{R}) \) 又包含自由群 \( F_2 \)（具有两个生成元）作为其子群。这使得巴拿赫-塔尔斯基悖论的证明在平面中得以模仿成为可能。这里的主要难点在于单位正方形在特殊线性群 \( SL(2, \mathbb{R}) \) 的作用下并不保持不变，因此不能像上述巴拿赫-塔尔斯基悖论证明的第三步那样，简单地将悖论性分解从群转移到正方形。此外，群的固定点带来了一些困难（例如，原点在所有线性变换下都是固定的）。这就是为什么冯·诺依曼使用了更大的群 \( SA_2 \)，包括平移，并且他在 1929 年构造了关于这个扩展群的单位正方形的悖论性分解。通过应用 Banach-Tarski 方法，正方形的悖论可以进一步强化如下：

　　 任何两个具有非空内部的欧几里得平面中的有界子集，在保持面积的仿射映射下是等分解的。

　　 正如冯·诺依曼所指出：\(^\text{[16]}\)

　　 “因此，在平面中，已经不存在一个非负的可加测度（对于该测度，单位正方形的测度为 1），该测度对所有 \( A_2 \) 中的变换保持不变。”

　　 进一步解释，这个问题的关键在于是否存在一个有限可加的测度（在某些变换下保持不变），这取决于允许哪些变换。平面中的 Banach 测度，在平移和旋转下保持不变，但对于非等距变换，即使它们保持多边形的面积，也不能保持测度不变。平面上的点（除了原点）可以分为两个稠密的集合，可以称为 \( A \) 和 \( B \)。如果给定多边形的 \( A \) 点通过某个保持面积的变换被变换，而 \( B \) 点通过另一个变换被变换，那么这两个集合可以变成两个新多边形中 \( A \) 点的子集。新的多边形的面积与旧的多边形相同，但这两个变换后的集合不能具有与之前相同的测度（因为它们只包含部分 \( A \) 点），因此不存在一个 “有效的” 测度。

　　 冯·诺依曼在研究 Banach-Tarski 现象过程中孤立出的群类，证明对许多数学领域非常重要：这些群是可容许群，或具有不变均值的群，包括所有有限群和所有可解群。一般而言，当用于等分解定义中的等价关系的群不是可容许群时，就会出现悖论性分解。

近期进展

6. 另见

7. 笔记

  1. 陶哲轩 (2011). 《测度论导论》(PDF). 第 3 页. 原(PDF)文件于 2021 年 5 月 6 日存档.
  2. Wagon, 推论 13.3
  3. 特雷弗·M·威尔逊 (2005 年 9 月). “巴拿赫-塔斯基悖论的一个连续运动版本：德格鲁特问题的解”. 《符号逻辑杂志》. 70 卷(第 3 期): 946–952. CiteSeerX 10.1.1.502.6600. doi:10.2178/jsl/1122038921. JSTOR 27588401. S2CID 15825008.
  4. 奥利维尔·勒鲁瓦 (1995). 《正则场所中的测度理论，或：巴拿赫-塔斯基悖论中的隐藏交集》 (报告). arXiv:1303.5631.
  5. 亚历克斯·辛普森 (2012 年 11 月 1 日). 《测度、随机性与子区域》. 《纯粹与应用逻辑年鉴》. 163 卷(第 11 期): 1642–1659. doi:10.1016/j.apal.2011.12.014. hdl:20.500.11820/47f5df74-8a53-452a-88c0-d5489ee5d659.
  6. 斯特凡·巴拿赫; 阿尔弗雷德·塔斯基 (1924). 《论点集分解为互相同余的部分》 (PDF). 《数学基础》(法语). 6: 244–277. doi:10.4064/fm-6-1-244-277.
  7. 拉斐尔·M·罗宾逊(1947). 《论球体的分解》. 《数学基础》. 34: 246–260. doi:10.4064/fm-34-1-246-260.（本文基于对豪斯多夫悖论的分析，解决了冯·诺依曼于 1929 年提出的问题。）
  8. 安东尼·莫尔斯 (1949). 《正方形是正规的》. 《数学基础》. 36: 35–39. doi:10.4064/fm-36-1-35-39. ISSN 0016-2736.
  9. 保罗·J·科恩 (1963). 《连续统假设的独立性》. 《美国国家科学院院刊》. 50 卷(第 6 期): 1143–1148. Bibcode:1963PNAS...50.1143C. doi:10.1073/pnas.50.6.1143. ISSN 0027-8424. PMC 221287. PMID 16578557.
  10. 瓦贡, 推论 13.3
  11. M·福尔曼; F·韦伦 (1991). 《哈恩-巴拿赫定理蕴含非勒贝格可测集的存在性》 (PDF). 《数学基础》. 138: 13–19. doi:10.4064/fm-138-1-13-19.
  12. 亚努什·帕夫利科夫斯基 (1991). 《哈恩-巴拿赫定理蕴含巴拿赫-塔斯基悖论》 (PDF). 《数学基础》. 138: 21–22. doi:10.4064/fm-138-1-21-22.
  13. 瓦贡, 第 16 页.
  14. 不变测度、扩展器与性质 T 马克西姆·贝尔热龙
  15. V·A·丘尔金 (2010). 《豪斯多夫-巴拿赫-塔斯基悖论的一个连续版本》. 《代数与逻辑》. 49 卷(第 1 期): 81–89. doi:10.1007/s10469-010-9080-y. S2CID 122711859.（俄语全文可通过 Mathnet.ru 页面获取。）
  16. 在第 85 页。冯·诺依曼，J. (1929)。“Zur allgemeinen Theorie des Masses”（PDF）。《Fundamenta Mathematicae》。13: 73–116。doi:10.4064/fm-13-1-73-116。
  17. Laczkovich, Miklós (1999)。“在 SL2(R)下的悖论集合”。《匈牙利科学大学数学学报》。Eötvös Sect. Math. 42: 141–145。
  18. Satô, Kenzi (2003)。“在平面上作用的局部交换自由群”。《Fundamenta Mathematicae》。180 (1): 25–34。doi:10.4064/fm180-1-3。
  19. Laczkovich, Miklós (1999)。“在 SL2(R)下的悖论集合”。《匈牙利科学大学数学学报》。Eötvös Sect. Math. 42: 141–145。
  20. Tomkowicz, Grzegorz（2011）。“一个分段线性变换自由群”。《Colloquium Mathematicum》。125（2）：141–146。doi:10.4064/cm125-2-1。
  21. Adams, John Frank（1954）。“关于球面的分解”。《伦敦数学会杂志》。29：96–99。doi:10.1112/jlms/s1-29.1.96。
  22. Mycielski, Jan（1955）。“关于球面悖论”。《Fundamenta Mathematicae》。42（2）：348–355。doi:10.4064/fm-42-2-348-355。
  23. Tomkowicz, Grzegorz（2017）。“关于满足多重全等关系的双曲平面分解”。《伦敦数学会通报》。49：133–140。doi:10.1112/blms.12024。S2CID 125603157。
  24. Mycielski, Jan（1989）。“双曲平面上的巴拿赫-塔斯基悖论”。《Fundamenta Mathematicae》。132（2）：143–149。doi:10.4064/fm-132-2-143-149。
  25. Mycielski, Jan；Tomkowicz, Grzegorz（2013）。“双曲平面上的巴拿赫-塔斯基悖论（Ⅱ）”。《Fundamenta Mathematicae》。222（3）：289–290。doi:10.4064/fm222-3-5。
  26. Tomkowicz, Grzegorz（2017）。“某些完备流形中的巴拿赫-塔斯基悖论”。《美国数学会会刊》。145（12）：5359–5362。doi:10.1090/proc/13657。
  27. Mycielski, Jan；Wagon, Stan（1984）。“等距变换的大自由群及其几何性质”。《L’Enseignement Mathématique》。30：247–267。
  28. Tomkowicz, Grzegorz（2018）。“一个适当不连续的仿射变换自由群”。《几何专刊》（*Geom. Dedicata*）。197：91–95。doi:10.1007/s10711-018-0320-y。S2CID 126151042。
  29. Mycielski, Jan；Tomkowicz, Grzegorz（2019）。“关于等测集通过可数分解的等价性”。《伦敦数学会通报》。51：961–966。doi:10.1112/blms.12289。S2CID 209936338。
  30. Simon, Robert；Tomkowicz, Grzegorz（2024）。“一个来自连续染色规则的测度论悖论”。《数学年刊》（*Math. Ann.*）。389（2）：1441–1462。arXiv:2203.11158。doi:10.1007/s00208-023-02644-4。
  31. Tomkowicz, Grzegorz（2024）。“关于有界悖论集合与李群的问题”。《几何专刊》（*Geom. Dedicata*）。218（3）：72。doi:10.1007/s10711-024-00923-1。

8. 参考文献

9. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利