布劳威尔不动点定理（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 布劳威尔不动点定理是拓扑学中的一个不动点定理，以 L. E. J.布劳威尔命名。该定理指出：对于任意一个将非空紧致凸集映射到其自身的连续函数 $f$，总存在一点 $x_0$，使得 $f(x_0) = x_0$。最简单的形式是将一个闭区间 $I$（实数集中的）映射到自身的连续函数，或将一个闭圆盘 $D$ 映射到自身的情形。比这更一般的形式是：将欧几里得空间中的非空紧致凸子集 $K$ 映射到自身的连续函数。

　　 在众多不动点定理中，\(^\text{[1]}\) 布劳威尔不动点定理尤为著名，部分原因是它在数学的众多领域中都有广泛应用。在其原始领域中，这一结果是刻画欧几里得空间拓扑性质的关键定理之一，与约旦曲线定理、毛球定理、维数不变性定理以及博苏克–乌拉姆定理并列为拓扑学的基本定理之一。\(^\text{[2]}\) 它还被用于证明关于微分方程的重要结论，因此通常出现在微分几何的入门课程中。此外，它也出现在一些出人意料的领域，比如博弈论。在经济学中，布劳威尔不动点定理及其推广——卡库塔尼不动点定理，是 20 世纪 50 年代经济学诺贝尔奖得主肯尼斯·阿罗和热拉尔·德布鲁提出的一般均衡存在性证明的核心工具。

　　 这一定理最初是在研究微分方程的背景下被法国数学家们提出的，代表人物有昂利·庞加莱和夏尔·埃米尔·皮卡尔。要证明诸如庞加莱–本迪克松定理这样的结果，需要运用拓扑方法。这一领域在 19 世纪末开启，催生了定理的若干版本。对于 $n$ 维闭球中可微映射的情形，最早由雅克·阿达马于 1910 年给出证明；而对连续映射的一般情形，则由布劳威尔于 1911 年完成证明。\(^\text{[5]}\)

1. 陈述

　　 布劳威尔不动点定理有多种表述方式，取决于其应用的上下文以及推广的程度。最简单的形式如下：

　　 在平面上

　　 每一个从闭圆盘映射到其自身的连续函数至少有一个不动点。\(^\text{[6]}\)

　　 这个结论可以推广到任意有限维度：

　　 在欧几里得空间中

　　 每一个从欧几里得空间中闭球映射到其自身的连续函数都有一个不动点。\(^\text{[7]}\)

　　 稍微更一般一点的版本是：

　　 凸紧致集

　　 每一个从欧几里得空间中非空凸紧致子集 $K$ 映射到自身的连续函数都有一个不动点。\(^\text{[9]}\)

　　 一个更加广义的形式通常以另一个名称广为人知：

　　 舍乌德尔不动点定理

　　 每一个从巴拿赫空间中非空凸紧致子集 $K$ 映射到自身的连续函数都有一个不动点。\(^\text{[10]}\)

2. 先决条件的重要性

　　 该定理仅对自同态函数（即定义域与值域相同的函数）成立，并且要求集合是非空、紧致（即有界并闭合）且凸的（或者与凸集同胚）。下面的示例将说明这些先决条件为何是必要的。

函数 $f$ 作为自同态映射的情况

　　 考虑函数 $$ f(x) = x + 1~ $$ 其定义域为 $[-1, 1]$，而值域为 $[0, 2]$。因此，$f$ 并不是一个**自同态映射**（即定义域和值域不同的函数）。

有界性

　　 考虑函数 $$ f(x) = x + 1~ $$ 这是一个从实数集 $\mathbb{R}$ 映射到自身的连续函数。由于它将每个点都向右平移，因此不可能存在不动点。空间 $\mathbb{R}$ 是凸的和闭合的，但它不是有界的。

闭合性

　　 考虑函数 $$ f(x) = \frac{x + 1}{2}~ $$ 这是一个从开区间 $(-1, 1)$ 映射到自身的连续函数。由于点 $x = 1$ 不属于该开区间，因此在定义域中不存在满足 $f(x) = x$ 的点，即该函数在开区间上没有不动点。集合 $(-1, 1)$ 是凸的、是有界的，但它不是闭合的。另一方面，函数 $f$ 在闭区间 $[-1, 1]$ 上确实有不动点，即 $x = 1$ 闭区间 $[-1, 1]$ 是紧致的（即同时是闭的和有界的），而开区间 $(-1, 1)$ 则不是。

凸性

　　 对于布劳威尔不动点定理而言，凸性并不是绝对必要的条件。因为该定理中涉及的属性（连续性、是否为不动点）在同胚变换下是不变的，所以布劳威尔不动点定理等价于那些将定义域要求为闭单位球 $D^n$ 的形式。出于同样的原因，定理也适用于任何与闭单位球同胚的集合（因此这些集合也是闭的、有界的、连通的、无洞的，等等）。

　　 下面这个例子说明了：布劳威尔不动点定理不适用于存在 “空洞” 的定义域。考虑函数 $f(x) = -x$ 它是一个从单位圆映射到自身的连续函数。由于对于单位圆上的任何点 $x$，都有 $-x \ne x$，因此 $f$ 没有不动点。类似的例子也适用于 $n$ 维球面（或者任何不包含原点的对称区域）。单位圆是闭合且有界的，但它存在一个空洞（因此不是凸的）。相反地，函数 $f$ 在单位圆盘内是有不动点的，因为它将原点映射为自己。

　　 对布劳威尔不动点定理在 “无洞” 区域上的形式推广，可以通过 Lefschetz 不动点定理来导出 \(^\text{[11]}\)。

注

　　 该定理中的连续函数不要求是双射或满射。

3. 插图说明

　　 布劳威尔不动点定理有一些 “现实世界” 的形象例证。以下是几个例子：

  1. 皱纸叠放
    拿两张大小相同的坐标方格纸，一张平铺在桌面上，另一张则不撕裂地揉皱，然后随意放置在那张平铺的纸上，只要揉皱纸的边界没有超出平铺纸的边缘，必然存在揉皱纸上的某个点正好位于平铺纸上相同坐标位置的正上方。 这是布劳威尔不动点定理在二维情形（$n = 2$）的一个推论，应用在这样一个连续映射上：它将揉皱纸上每个点的坐标，映射为其正下方平铺纸上对应点的坐标。
  2. 地图定位
    拿一张国家的普通地图，将它摊开放置在该国家的某个位置上，总会存在一个 “你在这里” 的点，地图上的这个点刚好对应实际国家中的同一个点。
  3. 鸡尾酒搅拌
    在三维情形中，布劳威尔不动点定理的一个结果是：无论你如何搅拌一杯美味的鸡尾酒（或奶昔），当液体静止下来时，总有一点液体回到了搅拌前在杯子里的同一位置。 前提是：每个点最终的位置是其初始位置的连续函数；搅拌后液体仍然处于原始体积之内；杯子的形状以及液体表面维持一个凸形状的空间。如果点了 “摇而非搅” 的鸡尾酒，这种搅动过程打破了 “凸性” 条件（因为摇晃过程中的液体状态处于非凸的惯性运动封闭体积中），那么定理将不再适用，此时液体的每个点都可能被移动到一个不同于原位置的地方。

4. 直观解释

布劳威尔的解释

　　 据说，这一定理起源于布劳威尔对一杯精品咖啡的观察。\(^\text{[12]}\) 当他搅拌咖啡以溶解一块方糖时，他注意到：似乎总有一个点是静止不动的。他据此得出结论：在任何时刻，液面上总存在一个没有运动的点。\(^\text{[13]}\) 不过，这个不动点未必是视觉上看起来静止的那个点，因为涡流的中心本身也会有轻微的移动。这个结果并不直观，因为原先的不动点在另一个不动点出现时可能会变得可动。

　　 据说布劳威尔还补充道：“我可以用另一种方式来表述这个精彩的结果：我拿一张水平的纸片，再拿一张一模一样的纸，把它揉皱，然后摊开，放在第一张纸上。那么，揉皱纸上必定存在一个点，它正好和下面那张纸上的对应点重合。”\(^\text{[13]}\) 布劳威尔所谓的 “摊开”，是像用熨斗那样将其压平，但不消除折痕和皱纹。不同于咖啡杯的例子，这个揉皱纸的例子还展示了可能存在不止一个不动点。这也使得布劳威尔的不动点定理与其他定理（如斯特凡·巴拿赫的不动点定理）区分开来，后者往往保证不动点的唯一性。

一维情况

图
图 1

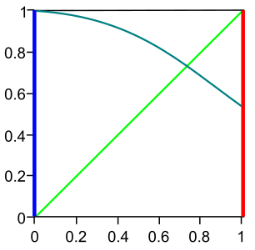
　　 在一维中，这一结果是直观且容易证明的。设有一个连续函数 $f$，定义在闭区间 $[a, b]$ 上，且函数值也落在该区间内。所谓函数有一个不动点，就是说它的图像（图中深绿色曲线）与定义在同一区间 $[a, b]$ 上的恒等函数 $x \mapsto x$（图中浅绿色对角线）相交。

　　 直观地看，任何从正方形左边到右边的连续曲线，必然会与那条绿色对角线相交。为了证明这一点，考虑函数 $g(x) = f(x) - x$。那么在端点 $a$ 处有 $g(a) \ge 0$，在 $b$ 处有 $g(b) \le 0$。根据**介值定理**，函数 $g$ 在区间 $[a, b]$ 上必有一个零点；这个零点就是一个不动点。

　　 据说布劳威尔曾这样表达这个观点：“我们不去研究一个表面，而是用一根绳子来说明这个定理。我们先把绳子拉直，再重新折叠它，然后将折叠后的绳子压平。一定存在一个点，其在压平后的位置与其在原始未折叠绳子中的位置保持一致。”\(^\text{[13]}\)

5. 历史

　　 布劳威尔不动点定理是代数拓扑学早期的重要成果之一，它奠定了后续一系列更一般不动点定理的基础，这些定理在泛函分析中具有重要意义。维数 $n = 3$ 的情形最早由皮尔斯·博尔于 1904 年证明，并发表在《纯粹与应用数学杂志》上 \(^\text{[14]}\)。随后，L. E. J. 布劳威尔于 1909 年也给出了证明。雅克·阿达马于 1910 年证明了一般情形 \(^\text{[4]}\)，而布劳威尔在同年也找到了一个不同的证明 \(^\text{[5]}\)。

　　 由于这些早期的证明都是非构造性的间接证明，因此与布劳威尔所倡导的 “直觉主义” 数学理念相悖。尽管布劳威尔定理所保证的不动点的存在并不是构造性的（在数学建构主义意义上），但如今已经发展出了近似计算这些不动点的方法 \(^\text{[15][16]}\)。

发现之前

图
图 2：该定理适用于任何圆盘形区域，并保证其中存在一个不动点。

　　 在 19 世纪末，关于太阳系稳定性的古老问题 \(^\text{[17]}\) 重新成为数学界关注的焦点。\(^\text{[18]}\) 要解决这一问题，需要全新的方法。正如亨利·庞加莱在研究三体问题时指出的那样，想要找到一个精确解几乎是不可能的：“没有什么比三体问题更能体现动力学中难题的棘手程度，特别是当不存在统一积分，而博林级数又发散时。”\(^\text{[19]}\) 他还指出，寻找近似解也同样无效：“我们越是试图得到精确的近似，结果反而会越来越不精确。”\(^\text{[20]}\)

图
图 3：对于在无界区域内的流动，或在具有“空洞”的区域内的流动，该定理不适用。

　　 他研究了一个类似 “咖啡杯中表面运动” 的问题：在一个由恒定流动驱动的表面上，轨迹的一般行为如何？\(^\text{[21]}\) 庞加莱发现，答案可归结于我们今天所说的 “包含轨迹区域的拓扑性质”。如果该区域是紧的（即既闭又有界），那么轨迹要么趋于静止，要么趋近于一个极限环。\(^\text{[22]}\) 庞加莱进一步指出：如果该区域的拓扑类型类似于圆盘（如咖啡杯液面），那么一定存在一个不动点。这个不动点在将初始点映射到短时间 $t$ 后的新位置的函数下是不变的。而如果区域是一个环形带，或不是封闭的，\(^\text{[23]}\) 那么就未必存在不动点。

　　 为了更好地理解微分方程，一个新的数学分支应运而生。庞加莱称其为 “位形分析”。《法兰西大百科全书》将其定义为研究 “在不撕裂对象的前提下，连续变形中保持不变的性质” 的数学分支。\(^\text{[24]}\) 早在 1886 年，庞加莱就已经证明了一个结果，其实质与布劳威尔不动点定理是等价的，\(^\text{[25]}\) 尽管当时他尚未意识到两者的联系。\(^\text{[26]}\) 此后不久，他发展出了一种更强有力的工具，用于理解位形分析——即如今所谓的 “基本群”，有时也称为 “庞加莱群”。\(^\text{[27]}\) 这种方法可用于对该不动点定理的一个非常简洁的证明。

　　 庞加莱的方法在思想上类似于他的同时代人埃米尔·皮卡尔的做法。皮卡尔推广了柯西–李普希茨定理，[28] 他的方法建立在一个后来被正式形式化并以 “巴拿赫不动点定理” 命名的结果之上。与庞加莱使用拓扑性质不同，皮卡尔的方法依赖于函数满足 “压缩映射” 性质。

最初的证明

　　 在 20 世纪初，拓扑分析逐渐引起人们的关注。然而，那时尚未意识到一个等价于本文所述定理的重要性。拉脱维亚数学家皮尔斯·博尔）将拓扑方法应用于微分方程的研究 \(^\text{[29]}\)。早在 1904 年，他就证明了该定理在三维情况下的成立 \(^\text{[14]}\)，但他的成果并未引起关注 \(^\text{[30]}\)。

　　 最终，是布劳威尔赋予了该定理崇高的地位。他的目标与庞加莱不同，这位数学家更关注数学基础问题，尤其是数理逻辑与拓扑。他最初的兴趣源于试图解决希尔伯特的第五问题 \(^\text{[31]}\)。1909 年，在一次巴黎之行中，他结识了亨利·庞加莱、雅克·阿达玛和埃米尔·博雷尔。此次交流使布劳威尔认识到深入理解欧几里得空间的重要性，并促成了他与阿达玛之间富有成果的书信往来。接下来的四年里，他专注于这方面若干重要定理的证明。1912 年，他证明了二维球面上的 “毛球定理”，以及任意连续映射将二维球映射到自身时必存在不动点的定理 \(^\text{[32]}\)。这两项结果本身并非全新。正如阿达玛所指出，庞加莱早已证明了一个与毛球定理等价的定理 \(^\text{[33]}\)。布劳威尔的革命性贡献在于他系统性地采用了当时刚发展出的数学工具，如同伦，这一概念正是庞加莱群（即基本群）的核心思想。次年，阿达玛将该定理推广到任意有限维空间，不过采用了不同的方法。汉斯·弗罗伊登塔尔对两者角色的评价是：“与布劳威尔革命性的方法相比，阿达玛的方法更为传统；但阿达玛在布劳威尔思想诞生中的作用更像是助产士，而非单纯的旁观者。”\(^\text{[34]}\)

　　 布劳威尔的方法很快结出硕果。1910 年，他也找到了一个适用于任意有限维空间的证明 \(^\text{[5]}\)，并由此推导出其他关键定理，如维度不变性定理 \(^\text{[35]}\)。在这一工作背景下，布劳威尔还将约旦曲线定理推广至任意维度，并建立了与连续映射的度数相关的基本性质 \(^\text{[36]}\)。这一数学分支，最初由庞加莱构想、由布劳威尔发展，后来在 1930 年代更名为代数拓扑 \(^\text{[37]}\)。

反响

图
图 4：约翰·纳什在博弈论中运用了该定理，以证明均衡策略组合的存在性。

　　 该定理的价值在多个方面得到了体现。20 世纪期间，数学界发展出了众多不动点定理，甚至形成了一个专门的数学分支——不动点理论 \(^\text{[38]}\)。在所有这些定理中，布劳威尔不动点定理大概是最重要的一个 \(^\text{[39]}\)。它也是拓扑流形拓扑结构的奠基性定理之一，常被用来证明其他重要结果，例如乔丹曲线定理 \(^\text{[40]}\)。

　　 除了适用于某些 “压缩” 映射的不动点定理之外，还有许多直接或间接从布劳威尔定理出发发展而来的定理。例如，一个从欧几里得空间中封闭球映射到其边界的连续映射，不可能在边界上是恒等映射。类似地，博苏克–乌拉姆定理指出，从 $n$ 维球面连续映射到 $\mathbb{R}^n$ 的函数，必然存在一对对踵点被映射到同一个点。在有限维情况下，勒夫谢茨不动点定理从 1926 年起提供了一种计数不动点的方法。到了 1930 年，布劳威尔不动点定理被推广到了巴拿赫空间 \(^\text{[41]}\)，这个推广版本被称为绍德尔不动点定理，而后又被 $S$. 柿谷进一步推广到值为集合的函数 \(^\text{[42]}\)。此外，在拓扑学以外的领域，人们也可以见到该定理及其变种的身影。它可用于证明哈特曼–格罗布曼定理，该定理描述了某些微分方程在特定平衡点附近的定性行为。同样地，布劳威尔定理还可用于证明中心极限定理。某些偏微分方程解的存在性证明中也能找到它的身影 \(^\text{[43]}\)。

　　 其他领域也受到了影响。在博弈论中，约翰·纳什使用该定理证明了在 Hex 游戏中白方必有必胜策略 \(^\text{[44]}\)。在经济学中，P. Bich 指出该定理的某些推广对于博弈论中的经典问题、一般均衡理论（如霍特林法则）、金融均衡以及不完全市场等问题具有重要价值 \(^\text{[45]}\)。

　　 布劳威尔的声望并不仅限于其拓扑学成果。他那几大拓扑定理的证明都不是构造性的 \(^\text{[46]}\)，这正是促使他提出 “构造性” 概念的重要动因。他由此成为直觉主义数学哲学的创始人和坚定捍卫者，这一思想体系当时是对集合论的直接挑战 \(^\text{[47]}\)。布劳威尔本人甚至否定了他最初给出的那个不动点定理的证明。

6. 证明概要

使用 “映射次数（degree）” 的证明

　　 布劳威尔在 1911 年给出的原始证明依赖于连续映射的 “映射次数” 这一概念，该概念源于微分拓扑中的思想。现代关于该证明的阐述可见于文献中，例如 Milnor（1965）【48】【49】。

　　 设 $K = \overline{B(0)}$ 表示以原点为中心的单位闭球，即 $\mathbb{R}^n$ 中的闭单位球。为简便起见，设 $f: K \to K$ 是一个连续可微的映射。一个点 $p \in B(0)$（单位开球）被称为 $f$ 的正则值，如果在 $f^{-1}(p)$ 的每个点上，$f$ 的雅可比矩阵是非奇异的（即可逆）。根据反函数定理，$f^{-1}(p)$ 中的每个点都位于 $B(0)$ 的内部（即 $K$ 的内部）。我们定义 $f$ 在正则值 $p \in B(0)$ 处的映射次数如下： $$ \deg_p(f) = \sum_{x \in f^{-1}(p)} \operatorname{sign} \det(df_x)~ $$ 其中 $df_x$ 表示在点 $x$ 处的微分，也就是雅可比矩阵，$\operatorname{sign} \det(df_x)$ 表示其行列式的符号（+1 或 -1）。

　　 这个 “次数” 粗略地说就是落在 $p$ 附近一个小开集上的 $f$ 原像有多少 “层”，如果这些 “层” 的方向相反，则它们将以相反的符号计数。这个概念可以视为将绕数推广到高维空间的方式。

　　 映射次数的性质与不动点的存在性证明

　　 映射次数满足同伦不变性这一重要性质：设 $f$ 和 $g$ 是两个连续可微的函数，定义同伦 $H_t(x) = t f(x) + (1 - t) g(x)$，其中 $0 \leq t \leq 1$。若点 $p$ 是每个 $H_t$ 的正则值，则有：$\deg_p f = \deg_p g$

　　 若函数 $f$ 在 $K$ 的边界上没有不动点（即 $f(x) \neq x$ 对所有 $x \in \partial K$ 成立），则可以定义如下函数： $$ g(x) = \frac{x - f(x)}{\sup_{y \in K} |y - f(y)|}~ $$ 该函数 $g$ 是良定义的，并可进一步构造同伦： $$ H(t, x) = \frac{x - t f(x)}{\sup_{y \in K} |y - t f(y)|}~ $$ 这定义了从恒等映射 $\text{id}(x) = x$ 到 $g(x)$ 的一个同伦。

　　 恒等映射在任意点（包括原点）上的映射次数是 1，因此由同伦不变性知：$\deg_0 g = 1 $ 于是其原像不为空：$g^{-1}(0) \neq \varnothing$ 而 $g(x) = 0$ 的解恰好满足 $x = f(x)$，即为原函数 $f$ 的不动点。

　　 进一步推广

　　 为了使该结论适用于所有连续函数，而不仅限于可微函数，还需将 “映射次数” 的定义扩展到包括奇异值（即雅可比奇异点）以及任意连续函数。这可以借助同调理论来完成，从而更简洁严密地构造映射次数。因此，现代数学中，布劳威尔不动点定理的证明常使用代数拓扑中的同调工具完成，成为文献中广泛接受的标准证明方式。

使用 “毛球定理” 的一种证明方法

　　 毛球定理断言：在奇维欧几里得空间中的单位球面 $S$ 上，不存在一个处处非零的连续切向量场 $\mathbf{w}$。（切向量场意味着：对于每个单位向量 $\mathbf{x}$，都有 $\mathbf{w}(\mathbf{x}) \cdot \mathbf{x} = 0$）。该定理有时也被形象地描述为：“地球上总有一个没有风的点”。Milnor（1978）中提供了该定理的一个初等证明。

　　 我们首先假设 $\mathbf{w}$ 是一个连续可微的切向量场。通过缩放，我们可以设 $\mathbf{w}$ 是单位切向量场，即满足 $\|\mathbf{w}(x)\| = 1$。我们将其沿径向扩展到靠近球面的一个小球壳区域 $A$。当 $t$ 足够小时，定义映射： $$ f_t(\mathbf{x}) = \mathbf{x} + t \mathbf{w}(\mathbf{x})~ $$ 易见其是 $A$ 上的一个压缩映射，其像的体积是关于 $t$ 的一个多项式。然而另一方面，由于压缩性质，$f_t$ 应该将 $S$ 同胚地映射到 $\sqrt{1 + t^2} \cdot S$，将 $A$ 映射到 $\sqrt{1 + t^2} \cdot A$。如果空间维度 $n$ 是奇数，那么 $(1 + t^2)^{n/2}$ 并不是一个多项式，这就导致矛盾。

　　 如果 $\mathbf{w}$ 只是一个连续的单位切向量场，那么根据 Weierstrass 逼近定理，它可以被逼近为一个从 $A$ 映射到欧几里得空间的多项式映射 $\mathbf{u}$。对其作正交投影得到：$\mathbf{v}(\mathbf{x}) = \mathbf{u}(\mathbf{x}) - (\mathbf{u}(\mathbf{x}) \cdot \mathbf{x}) \cdot \mathbf{x}$ 则 $\mathbf{v}$ 是一个在 $A$ 上处处非零的多项式切向量场，归一化后 $\mathbf{v} / \|\mathbf{v}\|$ 是一个光滑单位切向量场，这与毛球定理矛盾。

　　 将毛球定理用于布劳威尔不动点定理的证明

　　 假设维数 $n$ 是偶数。如果存在一个没有不动点的连续映射 $f$，从单位闭球 $B$ 映到自身，定义： $$ \mathbf{w}(\mathbf{x}) = (1 - \mathbf{x} \cdot \mathbf{f}(\mathbf{x})) \, \mathbf{x} - (1 - \mathbf{x} \cdot \mathbf{x}) \, \mathbf{f}(\mathbf{x})~ $$ 由于 $f$ 无不动点，内部点 $\mathbf{x}$ 满足 $\mathbf{w}(\mathbf{x}) \neq 0$，而在边界 $S$ 上有：$\mathbf{x} \cdot \mathbf{w}(\mathbf{x}) = 1 - \mathbf{x} \cdot \mathbf{f}(\mathbf{x}) > 0$ 我们构造辅助空间 $W = V \times \mathbb{R}$，其点为 $\mathbf{y} = (\mathbf{x}, t)$。定义向量场： $$ \mathbf{X}(\mathbf{x}, t) = (-t \, \mathbf{w}(\mathbf{x}), \, \mathbf{x} \cdot \mathbf{w}(\mathbf{x}))~ $$ 该向量场在 $W$ 的单位球面上连续，并满足切向量条件 $\mathbf{y} \cdot \mathbf{X}(\mathbf{y}) = 0$。而且 $\mathbf{X}$ 无零点（即处处非零），从而矛盾。故原假设不成立，存在不动点。

　　 奇数维情形怎么办？

　　 当 $n$ 为奇数时，可以考虑维数 $n+1$ 的单位闭球 $B$，并构造映射：$F(\mathbf{x}, y) = (f(\mathbf{x}), 0)$ 再应用偶数维的结果即可。

　　 结语

　　 这种证明仅使用初等技巧，不依赖代数拓扑中的深层工具（如 Borsuk–Ulam 定理），因此适合入门学习。而更一般的推广则需代数拓扑支持。

一种使用同调或上同调的证明方法

　　 该证明利用了这样一个观察：n 维圆盘 $D^n$ 的边界是 $S^{n-1}$，即 $(n-1)$ 维球面。

图
图 5：收缩映射 $F$ 的示意图

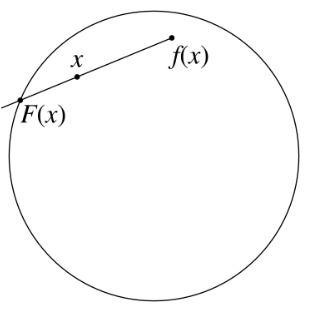
　　 假设，为了反证，我们有一个连续函数 $f : D^n \to D^n$，它没有不动点。这意味着对圆盘 $D^n$ 中的每一个点 $x$，点 $x$ 和 $f(x)$ 都是不同的。由于它们不同，我们可以从 $f(x)$ 朝着 $x$ 的方向作出一条唯一的射线，并沿着这条射线延伸，直到它与边界 $S^{n-1}$ 相交（见图示）。我们将这个交点记为 $F(x)$，于是定义了一个函数 $F : D^n \to S^{n-1}$，将圆盘中的每个点映射到其对应的边界交点。

　　 作为一个特殊情况，当 $x$ 本身就在边界上时，那么交点 $F(x)$ 必然就是 $x$ 本身。

　　 因此，函数 $F$ 是一种特殊类型的连续函数，被称为 “收缩映射”：即值域（在此为 $S^{n-1}$）中的每一个点在映射下都是一个不动点。

　　 直观上，我们会觉得将 $D^n$ 收缩映射到其边界 $S^{n-1}$ 是不可能的；对于 $n = 1$ 的情形，这一点甚至更加明显，因为 $S^0$（即闭区间 $D^1$ 的两个端点）甚至不是连通的。$n = 2$ 的情况就不那么显而易见了，但可以借助基本的代数拓扑工具来证明其不可能性：该收缩映射将诱导出一个从 $D^2$ 的基本群到 $S^1$ 的基本群的满射，而前者是平凡群（trivial group），而后者同构于整数群 $\mathbb{Z}$，这显然是不可能的。此外，$n = 2$ 的情况也可以通过与向量场不消失定理的矛盾来加以证明。

　　 然而，对于 $n > 2$ 的情形，证明这种收缩映射不可能存在就更为复杂。一种方法是使用同调群（homology groups）：我们知道 $H_{n-1}(D^n)$ 是平凡的，而 $H_{n-1}(S^{n-1})$ 是无限循环群（即 $\mathbb{Z}$）。这就表明不能存在这样的收缩映射，因为该映射将诱导一个从 $H_{n-1}(S^{n-1})$ 到 $H_{n-1}(D^n)$ 的单射群同态，这是不可能的。

　　 同样地，这种收缩映射的不可能性还可以通过欧几里得空间 $\mathbb{E}^n$ 的开子集的 de Rham 上同调来证明。对于 $n \geq 2$，点 $0$ 被去除后的空间 $U = \mathbb{E}^n \setminus \{0\}$ 的 de Rham 上同调在 0 次和 $n-1$ 次时是一维的，其余次上同调群为零。如果收缩映射存在，那么 $U$ 就必须是可收缩的，而这将导致其 $n-1$ 次的 de Rham 上同调为零，与实际情况矛盾 \(^\text{[51]}\)。

使用斯托克斯定理的证明

　　 与使用同调理论证明 Brouwer 不动点定理的思路类似，该证明也归结为证明不存在从球体 $B$ 到其边界 $\partial B$ 的连续收缩映射 $F$。在这种情况下，可以假设 $F$ 是光滑的，因为可以通过 Weierstrass 逼近定理，或者通过与具有足够小支集和单位积分的非负光滑 “凸起函数” 卷积（即 “平滑处理”）来逼近它。

　　 若 $\omega$ 是定义在边界上的体积形式，则由斯托克斯定理可得： $$ 0 < \int_{\partial B} \omega = \int_{\partial B} F^{*}(\omega) = \int_{B} dF^{*}(\omega) = \int_{B} F^{*}(d\omega) = \int_{B} F^{*}(0) = 0,~ $$ 这给出了一个矛盾。

　　 更一般地说，这说明不存在从任何非空、光滑、定向、紧致流形 $M$ 到其边界的光滑收缩映射。这个使用斯托克斯定理的证明与使用同调理论的证明密切相关，因为形式 $\omega$ 生成了 de Rham 上同调群 $H^{n-1}(\partial M)$，根据 de Rham 定理，该群与同调群 $H_{n-1}(\partial M)$ 同构 \(^\text{[52][53][54]}\)。

组合证明

　　 Brouwer 不动点定理（BFPT）可以借助于 Sperner 引理 进行证明。下面我们给出一个特殊情形的证明概要：设 $f$ 是从标准 $n$-单纯形（standard $n$-simplex） $$ \Delta^n = \left\{ P \in \mathbb{R}^{n+1} \,\middle|\, \sum_{i=0}^{n} P_i = 1 \text{ 且 } P_i \geq 0 \text{ 对所有 } i \right\}~ $$ 到其自身的函数。对于每一个点 $P \in \Delta^n$，有 $f(P) \in \Delta^n$ 因此，它们坐标之和相等： $$ \sum_{i=0}^{n} P_i = 1 = \sum_{i=0}^{n} f(P)_i~ $$ 由鸽巢原理可知，对于每一个 $P \in \Delta^n$，必存在某个索引 $j \in \{0, \ldots, n\}$，使得该维度上的坐标满足： $$ P_j \geq f(P)_j~ $$ 更进一步地，如果 $P$ 落在 $\Delta^n$ 的某个 $k$ 维子面（sub-face）上，那么同样的道理可以应用，且此时的索引 $j$ 可以从该子面上非零的 $k + 1$ 个坐标中选出。

　　 现在我们使用这个事实来构造一个 Sperner 染色。对于 $\Delta^n$ 的任意一个三角剖分，我们对每个顶点 $P$ 染色：颜色为一个满足 $f(P)_j \leq P_j$ 的索引 $j$。

　　 这种染色方式就是符合 Sperner 引理 的染色。由 Sperner 引理可知，必然存在一个 $n$ 维单纯形，其顶点被染上了 $n + 1$ 种不同的颜色。

　　 由于 $f$ 是连续的，当我们选择任意精细的三角剖分时，可以使这个单纯形足够小。因此，存在某个点 $P$，其所有坐标都满足：$f(P)_j \leq P_j \quad \text{对所有 } j$

　　 然而，由于 $P$ 与 $f(P)$ 的所有坐标之和都等于 1，因此上述所有不等式实际上都必须是等式，即：$f(P)_j = P_j \quad \text{对所有 } j$ 因此，我们得到： $$ f(P) = P~ $$ 即 $P$ 是函数 $f$ 的一个 不动点。这就是 Brouwer 不动点定理的结论。

赫希的证明方法

　　 还有一种简洁的证明方式，来自莫里斯·赫希，该方法基于 “不可微缩（不可微分收缩映射）” 的原理。设 $f$ 是从 $n$ 维欧几里得空间中的单位球 $D^n$ 映射到自身的连续函数，并假设 $f$ 没有不动点。由于 $f$ 连续且 $D^n$ 是紧致的，可以推出存在某个 $\varepsilon > 0$，使得对于所有 $x \in D^n$，都有 $\|x - f(x)\| > \varepsilon$ 接下来，可以通过 Weierstrass 逼近定理 或使用带光滑支撑的 bump 函数进行卷积，将 $f$ 逼近为一个光滑函数，并且保留 “没有不动点” 的性质。此时，可以像先前那样定义一个收缩映射：将 $x$ 映射为从 $x$ 指向 $f(x)$ 的射线与 $\partial D^n$（球面边界）交点，这样我们得到一个从 $D^n$ 到 $\partial D^n$ 的光滑映射。 根据 Sard 定理，该收缩映射必须在边界 $\partial D^n$ 上存在一个正则值 $p$，该点在边界上的限制映射（即恒等映射）也是正则的。于是，点 $p$ 的原像 $f^{-1}(p)$ 将是一个带边界的一维流形（1-manifold with boundary）。这样的流形的边界至少包含两个端点，而这些端点必须落在原始球体的边界上。这意味着：单位球边界 $\partial D^n$ 上的一个点的原像中包含另一个边界点，这与定义中的收缩映射 $D^n \to \partial D^n$ 相矛盾。因为收缩映射要求对边界点的原像只能是它自身。

　　 R. Bruce Kellogg、Tien-Yien Li 和 James A. Yorke 将 Hirsch 的证明转化为一个可计算的证明。他们指出：这个收缩映射实际上在除了不动点以外的所有地方都定义良好。对于几乎所有边界上的点 $q$（假设不是不动点），上述所说的一维流形确实存在，而且唯一的可能是从 $q$ 通向某个不动点。这就构成了一条轨迹。由于从 $q$ 追踪这条路径直到不动点在数值上是很容易实现的，因此这个方法本质上是可计算的。他们还提出了一个概念上类似的、基于同伦证明的路径追踪版本，可以推广到许多相关问题中。

使用有向面积的证明

　　 在不依赖于萨德定理的情况下，有一种上述证明的变体如下：若 $r: B \to \partial B$ 是一个光滑的收缩映射，我们考虑一个光滑的变形：$g^t(x) := t r(x) + (1 - t)x$ 并定义如下的光滑函数： $$ \varphi(t) := \int_B \det Dg^t(x)\,dx~ $$ 在积分符号下求导可以验证，$\varphi'(t) = 0$ 对所有 $t$ 都成立，因此 $\varphi(t)$ 是一个常数函数。但这导致矛盾，因为 $\varphi(0)$ 是单位球的 $n$ 维体积，而 $\varphi(1) = 0$。几何直观是：$\varphi(t)$ 表示 $g^t(B)$ 的有向面积（即：球经过 $g^t$ 映射后的 Lebesgue 测度，考虑重数与方向），在连续变形中应保持不变（在一维情形中尤为明显）。然而，随着参数 $t$ 从 0 变到 1，$g^t$ 从单位映射逐渐变成收缩映射 $r$，而 $r$ 的像落在球的边界上，边界是零测度集合，导致 $\varphi(1) = 0$，因此矛盾出现。

使用游戏 Hex 的证明

　　 David Gale 给出了一种完全不同的证明，基于棋类游戏 Hex。关于 Hex 的基本定理（最早由 John Nash 证明）是：Hex 不可能出现平局；先手总有必胜策略（虽然该定理是不可构造的，对于 $10 \times 10$ 或更大的棋盘，至今尚无完整策略）。这个结论实际上等价于二维 Brouwer 不动点定理。推广到 $n$ 维的 Hex 游戏，可以证明 Brouwer 定理在一般维度上等价于 Hex 的确定性定理。

使用 Lefschetz 不动点定理的证明

　　 Lefschetz 不动点定理指出，如果 $f$ 是一个从有限单纯复形 $B$ 映射到自身的连续映射，并且它只有孤立的不动点，那么不动点的 “带重数计数”（重数可能为负）等于 Lefschetz 数： $$ \sum_n (-1)^n \operatorname{Tr}(f|H_n(B))~ $$ 特别地，若 Lefschetz 数不为零，则 $f$ 必有不动点。若 $B$ 是一个球（或者更一般地是可收缩空间），那么 Lefschetz 数为 1，因为它唯一非零的单纯同调群是 $H_0(B)$，而 $f$ 在该群上作为恒等映射作用，因此 $f$ 存在不动点。

在弱逻辑系统中的证明

　　 在 “逆数学” 框架中，Brouwer 不动点定理可以在系统 WKL₀ 中证明。同时，在基础系统 RCA₀ 上，Brouwer 关于单位方形的定理反过来也可以推出弱 König 引理，从而精确刻画了 Brouwer 不动点定理的逻辑强度。

7. 推广

　　 布劳威尔不动点定理是许多更一般形式不动点定理的出发点。最直接的推广是将其应用于无限维空间，例如用任意希尔伯特空间的单位球代替欧几里得空间。然而，这种推广并不成立。主要问题在于：无限维希尔伯特空间中的单位闭球不是紧的。例如，在希尔伯特空间 ℓ²（即所有平方可和实数或复数序列的空间）中，考虑如下从 ℓ² 的单位闭球映射到自身的函数 $f : \ell^2 \to \ell^2$，它将序列 $(x_n)$ 映射到序列 $(y_n)$，定义为： $$ y_0 = \sqrt{1 - \|x\|_2^2}, \quad y_n = x_{n-1} \quad \text{对于 } n \geq 1~ $$ 不难验证，这个映射是连续的，其值域在 ℓ² 的单位球面上，但它没有不动点。

　　 因此，布劳威尔不动点定理在无限维空间中的各种推广都必须加入某种形式的紧致性假设，通常还需要凸性假设。关于这类定理的讨论，详见 “无限维空间中的不动点定理”。

　　 布劳威尔定理在有限维空间中也有进一步推广，适用于更广泛的空间类别：如果 $X$ 是有限多个可链连续统的笛卡尔积，那么对于任意连续映射 $f: X \rightarrow X$，都存在不动点。

　　 其中，可链连续统是指一个（通常但并非必须是度量空间的）紧致豪斯多夫空间，其任意开覆盖都存在一个有限开覆盖 $\{U_1, \dots, U_m\}$，满足只有当 $|i - j| \leq 1$ 时，$U_i \cap U_j \neq \emptyset$。这类空间的例子包括紧致连通的线性有序空间，特别是实数的闭区间。

　　 Kakutani 不动点定理是布劳威尔定理的另一方向推广：它仍在 $\mathbb{R}^n$ 中，但考虑的是上半连续的集合值函数（即将集合中的每个点映射到该集合的子集的函数）。它同样要求集合是紧的且是凸的。

　　 Lefschetz 不动点定理适用于（几乎）任意紧致拓扑空间，并给出了一个以奇异同调为条件的不动点存在判据；在单位 $n$ 维闭球 $D^n$ 的情形下，该条件恒成立，因此也就推出了布劳威尔不动点定理。

8. 等价结果

　　 有若干不动点定理存在三种等价变体：一种是代数拓扑版本，一种是组合版本，还有一种是集合覆盖版本。每种变体都可以通过完全不同的方法单独证明，但同一行中的任意一种变体也都可以归约为该行中的其他两种。此外，顶行中的每一个结果也都可以从同一列中其下方的结果推导出来 \(^\text{[63]}\)。

图
图 6

9. 参见

10. 注释

  1. 例如：F 与 V·Bayart，《Théorèmes du point fixe》，载于 [Bibm@th.net](mailto:Bibm@th.net)，[已于 2008 年 12 月 26 日存档于 Wayback Machine]。
  2. 参见 D. Leborgne《Calcul différentiel et géométrie》第 15 页，Puf 出版社（1982），ISBN 2-13-037495-6。
  3. 更准确地说，根据《Encyclopédie Universalis》：“Il en a démontré l'un des plus beaux théorèmes, le théorème du point fixe, dont les applications et généralisations, de la théorie des jeux aux équations différentielles, se sont révélées fondamentales.”（他证明了最优美的定理之一，即不动点定理，其在博弈论到微分方程的应用和推广被证明是基础性的。）——引自 G. Sabbagh 撰写的《Luizen Brouwer》。
  4. 雅克·阿达玛（：《关于克罗内克指标若干应用的笔记》，收录于 Jules Tannery 编著《单变量函数理论导论》（Introduction à la théorie des fonctions d'une variable，第 2 卷），第二版，A. Hermann & Fils 出版，巴黎 1910 年，第 437–477 页（法文）。
  5. 布劳威尔（Brouwer, L. E. J.）(1911)，《Über Abbildungen von Mannigfaltigkeiten》（关于流形的映射），载《Mathematische Annalen》（德文），第 71 卷，第 97–115 页，doi:10.1007/BF01456931，S2CID 177796823。
  6. D. Violette，《Sperner 引理在三角形中的应用》（Applications du lemme de Sperner pour les triangles），《Bulletin AMQ》，第 XLVI 卷第 4 期（2006），第 17 页。[已于 2011 年 6 月 8 日存档于 Wayback Machine]
  7. D. Leborgne《Calcul différentiel et géométrie》第 15 页，Puf 出版社（1982），ISBN 2-13-037495-6。
  8. 本版本直接从前述版本推出，因为欧几里得空间中每个凸紧子集都与与其维度相同的闭球同胚；参见 Monique Florenzano (2003)，《General Equilibrium Analysis: Existence and Optimality Properties of Equilibria》，Springer，第 7 页，ISBN 9781402075124，检索日期：2016-03-08。
  9. V. 与 F·Bayart，《Point fixe, et théorèmes du point fixe》，载于 Bibmath.net，[已于 2008 年 12 月 26 日存档于 Wayback Machine]。
  10. C. Minazzo 与 K. Rider，《不动点定理及其在微分方程中的应用》，尼斯-索菲亚·安提波利斯大学，[已于 2018-04-04 存档于 Wayback Machine]。
  11. Jim Belk，《为什么凸性是布劳威尔不动点定理的必要条件？》（Why is convexity a requirement for Brouwer fixed points?），Math StackExchange，检索于 2015 年 5 月 22 日。
  12. 该轶事的意义在于其直观性和教学价值，但其真实性值得怀疑。如历史部分所示，该定理的起源并非布劳威尔的工作。早在 20 多年前，庞加莱就已证明了一个等价的结果，而在布劳威尔之前五年，P·博尔已证明了三维情形。
  13. 此引述最初来自一档电视节目：Archimède，Arte，1999 年 9 月 21 日。
  14. 博尔（1904），“Über die Bewegung eines mechanischen Systems in der Nähe einer Gleichgewichtslage”（关于机械系统在平衡位置附近的运动），《J. Reine Angew. Math.》第 127 卷第 3/4 期，第 179–276 页。
  15. Stephan Karamardian (1977)，《Fixed points: algorithms and applications》，纽约：Academic Press，ISBN 978-0-12-398050-2。
  16. Vasile Istrăţescu (1981)，《Fixed point theory》，多德雷赫特-波士顿：D. Reidel Publishing Co.，ISBN 978-90-277-1224-0。
  17. 参见 F. Brechenmacher，《L'identité algébrique d'une pratique portée par la discussion sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des planètes》（通过讨论用于确定行星长期不等式的方程而形成的实践的代数身份），法国国家科学研究中心（CNRS）北加来海峡数学研究联合会。
  18. 亨利·庞加莱于 1889 年因其在三体问题相关研究方面的工作赢得了瑞典国王设立的数学竞赛奖项：引自 Jacques Tits，《2004 年国家纪念活动》，法国文化与传播部网站。
  19. 亨利·庞加莱，《天体力学的新方法》，T·戈捷-维拉尔出版社，第 3 卷，第 389 页（1892）；1987 年布朗沙尔出版社巴黎新版。
  20. 引自亨利·庞加莱的一段话，原文载于：P. A. Miquel，《无序范畴》，[2016 年 3 月 3 日存档于 Wayback Machine]，发布于 “法语人文学科研究人员协会” 网站。
  21. 该问题在以下文章中进行了研究：Poincaré, H.（1886），“论由微分方程定义的曲线”，《纯与应用数学杂志》，第 2 系第 4 卷，第 167–244 页。
  22. 这一结论源于庞加莱–本迪克松定理。
  23. 在区间 ]0, 1[^2 上的数乘变换 x ↦ x/2 没有不动点。
  24. “研究的是当一个图形被任意连续地变形（例如球面的变形）而不撕裂时，其不变量性质（例如球面上绘制的对象的相关性质）。” 引自：C. Houzel、M. Paty，《庞加莱，亨利（1854–1912）》，《大英百科全书》，阿尔班·米歇尔出版社，巴黎，1999 年，第 696–706 页，[2010 年 10 月 8 日存档于 Wayback Machine]。
  25. 庞加莱定理的表述见：V. I. Istratescu，《不动点理论导论》（Fixed Point Theory: An Introduction），Kluwer Academic Publishers（2001 年再版），第 113 页，ISBN 1-4020-0301-3。
  26. Voitsekhovskii, M.I.（2001）[1994]，“Brouwer 定理”，收录于《数学百科全书》（Encyclopedia of Mathematics），EMS Press，ISBN 1-4020-0609-8。
  27. 让·迪厄多内（1989），《代数与微分拓扑史，1900–1960》，波士顿：Birkhäuser，第 17–24 页，ISBN 978-0-8176-3388-2。
  28. 例如，参见：Émile Picard，《关于将逐次逼近法应用于某些常微分方程研究的探讨》，载于《数学杂志》，第 217 页（1893 年）[2011 年 7 月 16 日存档于 Wayback Machine]。
  29. J. J. O'Connor 和 E. F. Robertson 编写的关于 Piers Bohl 的传记。
  30. Myskis, A. D. 与 Rabinovic, I. M.（1955）：《拉脱维亚数学家 P. G. Bohl 首次证明将球面连续映射到自身的情形下的不动点定理》，载于《数学科学进展》（俄文），第 10 卷第 3 期，第 188–192 页。
  31. J. J. O'Connor 和 E. F. Robertson 编写的关于 Luitzen Egbertus Jan Brouwer 的传记。
  32. Hans Freudenthal（1975）：“现代拓扑学的摇篮，依据 Brouwer 的未刊稿”，载于《数学史》，第 2 卷第 4 期，第 495–502 页 [第 495 页]。doi:10.1016/0315-0860(75)90111-1。
  33. 同上文，第 501 页。文中指出：“虽然在更粗略的假设下，这一性质已由 H. Poincaré 证明。”
  34. 如果流形的一个开子集与 n 维欧几里得空间的一个开子集同胚，而 p 是正整数但不等于 n，则该开子集绝不可能与 p 维欧几里得空间的开子集同胚。
  35. J. J. O'Connor 和 E. F. Robertson 的关于 Brouwer 的文章。
  36. “代数拓扑” 一词最早出现于 1931 年，由 David van Dantzig 提出：J. Miller，《拓扑代数》，收录于 “数学词汇的最早已知用法” 网站（2007）。
  37. V. I. Istratescu，《不动点理论导论》，Kluwer Academic Publishers（2001 年新版），ISBN 1-4020-0301-3。
  38. “……Brouwer 不动点定理，也许是不动点定理中最重要的一个。” ——摘自 V. I. Istratescu，《不动点理论导论》，第 xiii 页。
  39. 例如：S. Greenwood 与 J. Cao，《Brouwer 不动点定理与约旦曲线定理》，奥克兰大学（新西兰）。
  40. Schauder, J.（1930）：《函数空间中的不动点定理》，载于《数学研究》，第 2 卷，第 171–180 页。doi:10.4064/sm-2-1-171-180。
  41. Kakutani, S.（1941）：《Brouwer 不动点定理的一种推广》，载于《杜克数学杂志》，第 8 卷第 3 期，第 457–459 页。doi:10.1215/S0012-7094-41-00838-4。
  42. 这些例子引自：F. Boyer，《不动点定理及其应用》，CMI，保罗·塞尚大学（2008–2009）[2010 年 8 月 1 日存档于 WebCite]。
  43. 有关背景和参考资料，参见 “六角棋（Hex）” 词条。
  44. P. Bich，《Schauder 不动点定理的不连续扩展及其在经济学中的若干应用》，庞加莱研究所，巴黎（2007 年）[2011 年 6 月 11 日存档于 Wayback Machine]。
  45. 有关详细解释，参见：J. P. Dubucs（1988），“L. J. E. Brouwer：拓扑与构造主义”，载于《科学史评论》，第 41 卷第 2 期，第 133–155 页。doi:10.3406/rhs.1988.4094。
  46. 后来人们发现，Brouwer 反对的形式主义在适当修改后也可以用于形式化直觉主义。更多内容可参见 “构造集合论”。
  47. Milnor（1965），第 1–19 页。
  48. Gerald Teschl（2019）：“第 10 章 Brouwer 映射度”，载于《线性与非线性泛函分析专题》（PDF），美国数学学会，《研究生数学导读》系列，[2022-10-09 PDF 存档]，2022 年 2 月 1 日访问。
  49. Milnor（1978）。
  50. Madsen & Tornehave（1997），第 39–48 页。
  51. Boothby（1971）。
  52. Boothby（1986）。
  53. Dieudonné（1982）。
  54. Hirsch（1988）。
  55. Kellogg、Li 与 Yorke（1976）。
  56. Chow、Mallet-Paret 与 Yorke（1978）。
  57. Kulpa（1989）。
  58. David Gale（1979）：“六角棋游戏与 Brouwer 不动点定理”，《美国数学月刊》，第 86 卷第 10 期，第 818–827 页。doi:10.2307/2320146。JSTOR 2320146。
  59. Hilton 与 Wylie（1960）。
  60. Spanier（1966）。
  61. Eldon Dyer（1956）：“一个不动点定理”，载于《美国数学学会会刊》，第 7 卷第 4 期，第 662–672 页。doi:10.1090/S0002-9939-1956-0078693-4。
  62. Kathryn L. Nyman 与 Francis Edward Su（2013），“一个可直接推出 Sperner 引理的 Borsuk–Ulam 等价命题”，《美国数学月刊》，第 120 卷第 4 期，第 346–354 页。doi:10.4169/amer.math.monthly.120.04.346。JSTOR 10.4169/amer.math.monthly.120.04.346。MR 3035127。

11. 参考文献

12. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利