安培力定律（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在静磁学中，两根载流导线之间的吸引或排斥力（见下方第一幅图）通常被称为安培力定律。这种力的物理来源是每根导线根据毕奥-萨伐尔定律产生磁场，而另一根导线则根据洛伦兹力定律受到磁力作用。

1. 公式

特殊情况：两条直平行导线

　　 安培力定律中最为人熟知且最简单的例子（在 2019 年 5 月 20 日之前[1]）用来定义电流的国际单位制（SI）单位安培。该定律表述，两条直平行导线之间的每单位长度的磁力为： \[ \frac{F_m}{L} = 2k_{\text{A}} \frac{I_1 I_2}{r},~ \] 其中：\( k_{\text{A}} \) 是由毕奥-萨伐尔定律定义的磁力常数；\( \frac{F_m}{L} \) 是单位长度上的总磁力（在较短导线上，较长导线被近似为相对于较短导线无限长）；\( r \) 是两导线之间的距离；\( I_1 \) 和 \( I_2 \) 是两导线中传输的直流电流。

　　 这种公式在以下情况下是良好的近似：如果一根导线的长度远大于另一根，可以将较长的导线近似为无限长； 如果两根导线之间的距离相对于导线的长度较小（使得无限长导线近似成立），但同时相对于导线的直径又较大（使得导线可以被近似为无限细的线）。\( k_{\text{A}} \) 的值取决于所选的单位系统，而 \( k_{\text{A}} \) 的值决定了电流单位的大小。

　　 在国际单位制（SI）中[2][3]： \[ k_{\text{A}} = \frac{\mu_0}{4\pi},~ \] 其中：\( \mu_0 \) 是磁常数（在国际单位中，称为真空磁导率）。

　　 SI 单位中，磁常数的值为： \[ \mu_0 = 1.25663706212(19) \times 10^{-6} \, \text{H/m}.~ \]

一般情况

　　 针对任意几何形状的磁力的一般公式基于迭代线积分，并将毕奥-萨伐尔定律和洛伦兹力结合在一个公式中，具体如下：[4][5][6] \[ \mathbf{F}_{12} = \frac{\mu_0}{4\pi} \int_{L_1} \int_{L_2} \frac{I_1 d\boldsymbol{\ell}_1 \times \left( I_2 d\boldsymbol{\ell}_2 \times \hat{\mathbf{r}}_{21} \right)}{|r|^2},~ \] 其中：

　　 若需确定材料介质中导线之间的磁力，则需要将磁常数 \( \mu_0 \) 替换为介质的实际磁导率。

　　 通过展开向量三重积并应用斯托克斯定理，该定律可以以以下等效形式重写：[7] \[ \mathbf{F}_{12} = -\frac{\mu_0}{4\pi} \int_{L_1} \int_{L_2} \frac{\left( I_1 d\boldsymbol{\ell}_1 \cdot I_2 d\boldsymbol{\ell}_2 \right) \hat{\mathbf{r}}_{21}}{|r|^2}.~ \] 在这种形式下，可以立即看出，由导线 2 对导线 1 施加的力与由导线 1 对导线 2 施加的力大小相等方向相反，这与牛顿第三定律一致。

2. 历史背景

图
图 1：安培原始实验的示意图

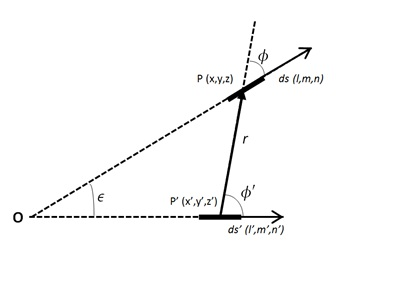
　　 1873 年，詹姆斯·克拉克·麦克斯韦推导出了通常表述的安培力定律，这是与安培和高斯的原始实验一致的多种表达式之一。关于两个直线电流 \(I\) 和 \(I'\) 之间的力的 \(x\) 分量（见相邻图示），安培在 1825 年和高斯在 1833 年分别给出了如下公式：[8] \[ dF_x = kII' ds' \int ds \frac{ \cos\left(x ds\right) \cos\left(r ds'\right) - \cos\left(rx\right) \cos\left(ds ds'\right) }{r^2}.~ \] 安培之后，众多科学家（包括威廉·韦伯、鲁道夫·克劳修斯、麦克斯韦、伯恩哈德·黎曼、赫尔曼·格拉斯曼和瓦尔特·里茨）对这一表达式进行了发展，试图寻找磁力的基本表达式。通过微分计算可以得到： \[ \frac{ \cos\left(x\,ds\right) \cos\left(r\,ds'\right) }{r^2} = - \cos\left(rx\right) \frac{\cos \varepsilon - 3 \cos \phi \cos \phi'}{r^2},~ \] 以及： \[ \frac{ \cos\left(rx\right) \cos\left(ds\,ds'\right) }{r^2} = \frac{ \cos\left(rx\right) \cos \varepsilon}{r^2}.~ \] 基于这些表达式，安培力定律可以进一步表示为： \[ dF_x = kII' ds' \int ds' \cos\left(rx\right) \frac{2 \cos \varepsilon - 3 \cos \phi \cos \phi'}{r^2}.~ \] 此外，使用以下关系： \[ \frac{\partial r}{\partial s} = \cos \phi,\ \frac{\partial r}{\partial s'} = -\cos \phi',~ \] 以及： \[ \frac{\partial^2 r}{\partial s \partial s'} = \frac{-\cos \varepsilon + \cos \phi \cos \phi'}{r}.~ \] 可以将安培的结果表示为： \[ d^2F = \frac{kII' ds ds'}{r^2} \left( \frac{\partial r}{\partial s} \frac{\partial r}{\partial s'} - 2r \frac{\partial^2 r}{\partial s \partial s'} \right).~ \] 麦克斯韦指出，该表达式中可以添加关于函数 \(Q(r)\) 的导数项，这些项在积分时会相互抵消。麦克斯韦给出了与实验事实一致的 “最通用形式”： \[ d^2F_x = kII' ds ds' \frac{1}{r^2} \left[ \left( \frac{\partial r}{\partial s} \frac{\partial r}{\partial s'} - 2r \frac{\partial^2 r}{\partial s \partial s'} + r \frac{\partial^2 Q}{\partial s \partial s'} \right) \cos\left(rx\right) + \frac{\partial Q}{\partial s'} \cos\left(x\,ds\right) - \frac{\partial Q}{\partial s} \cos\left(x\,ds'\right) \right].~ \]

　　 麦克斯韦指出，对于一个封闭电路，函数 \(Q(r)\) 的形式无法通过实验直接确定。假设 \(Q(r)\) 的形式为： \[ Q = -\frac{(1+k)}{2r}.~ \] 我们得到 ds 上由 ds' 施加的力的一般表达式： \[ d^{2}\mathbf{F} = -\frac{kII'}{2r^{2}} \left[ \left(3-k\right)\hat{\mathbf{r}}_{1}\left(d\mathbf{s} \, d\mathbf{s}'\right) - 3\left(1-k\right)\hat{\mathbf{r}}_{1}\left(\hat{\mathbf{r}}_{1} d\mathbf{s}\right)\left(\hat{\mathbf{r}}_{1} d\mathbf{s}'\right) - \left(1+k\right)d\mathbf{s}\left(\hat{\mathbf{r}}_{1} d\mathbf{s}'\right) - \left(1+k\right)d\mathbf{s}'\left(\hat{\mathbf{r}}_{1} d\mathbf{s}\right) \right].~ \] 通过对 \(s'\) 的积分可以消去 \(k\)，从而恢复安培和高斯给出的原始表达式。因此，就安培的原始实验而言，\(k\) 的取值并没有实际意义。安培取 \(k = -1\)；高斯取 \(k = +1\)，格拉斯曼和克劳修斯也取 \(k = +1\)，不过克劳修斯忽略了 \(S\) 分量。在非以太电子理论中，韦伯取 \(k = -1\)，而黎曼取 \(k = +1\)。里兹在其理论中未明确指定 \(k\) 的值。如果取 \(k = -1\)，我们得到安培的表达式： \[ d^{2}\mathbf{F} = -\frac{kII'}{r^{3}}\left[2\mathbf{r}(d\mathbf{s} \, d\mathbf{s'}) - 3\mathbf{r}(\mathbf{r} d\mathbf{s})(\mathbf{r} d\mathbf{s'})\right]~ \] 如果取 \(k=+1\)，我们得到： \[ d^{2}\mathbf{F} = -\frac{kII'}{r^{3}}\left[\mathbf{r}(d\mathbf{s} \, d\mathbf{s'}) - d\mathbf{s}(\mathbf{r} \, d\mathbf{s'}) - d\mathbf{s'}(\mathbf{r} \, d\mathbf{s})\right]~ \]

　　 利用三重叉积的矢量恒等式，可以将结果表示为： \[ d^{2}\mathbf{F} = \frac{kII'}{r^{3}}\left[\left(d\mathbf{s} \times d\mathbf{s'} \times \mathbf{r}\right) + d\mathbf{s'}(\mathbf{r} \, d\mathbf{s})\right]~ \] 对 \(d\mathbf{s'}\) 积分时，第二项为零，因此可以得到麦克斯韦形式的安培力定律： \[ \mathbf{F} = kII'\iint \frac{d\mathbf{s} \times (d\mathbf{s'} \times \mathbf{r})}{|r|^{3}}~ \]

3. 从一般公式推导平行直导线的情形

　　 从一般公式开始： \[ \mathbf{F}_{12} = \frac{\mu_{0}}{4\pi} \int_{L_{1}} \int_{L_{2}} \frac{I_{1} d\boldsymbol{\ell}_{1} \times (I_{2} d\boldsymbol{\ell}_{2} \times \hat{\mathbf{r}}_{21})}{|r|^{2}},~ \] 假设导线 2 位于 \(x\)-轴上，导线 1 位于 \(y=D, z=0\)，与 \(x\)-轴平行。令 \(x_1, x_2\) 分别表示导线 1 和导线 2 的微小线元的 \(x\)-坐标。换句话说，导线 1 的微小线元位于 \((x_1, D, 0)\)，而导线 2 的微小线元位于 \((x_2, 0, 0)\)。根据线积分的性质：\(d\boldsymbol{\ell}_1 = (dx_1, 0, 0)\) 且 \(d\boldsymbol{\ell}_2 = (dx_2, 0, 0).\)

　　 此外， \[\hat{\mathbf{r}}_{21} = \frac{1}{\sqrt{(x_1-x_2)^2 + D^2}}(x_1-x_2, D, 0),~\] 且 \[|r| = \sqrt{(x_1-x_2)^2 + D^2}.~\] 因此积分为： \[ \mathbf{F}_{12} = \frac{\mu_0 I_1 I_2}{4\pi} \int_{L_1} \int_{L_2} \frac{(dx_1, 0, 0) \times \left[(dx_2, 0, 0) \times (x_1-x_2, D, 0)\right]}{|(x_1-x_2)^2 + D^2|^{3/2}}.~ \] 计算叉积： \[ \mathbf{F}_{12} = \frac{\mu_0 I_1 I_2}{4\pi} \int_{L_1} \int_{L_2} dx_1 dx_2 \frac{(0, -D, 0)}{|(x_1-x_2)^2 + D^2|^{3/2}}~ \] 接下来对 \(x_2\) 从 \(-\infty\) 到 \(+\infty\) 积分： \[ \mathbf{F}_{12} = \frac{\mu_0 I_1 I_2}{4\pi} \frac{2}{D}(0, -1, 0) \int_{L_1} dx_1.~ \] 如果导线 1 也是无限长的，则积分会发散，因为两条无限长平行导线之间的总吸引力是无限大的。实际上，我们真正关心的是导线 1 单位长度上的吸引力。因此，假设导线 1 有一个很大但有限的长度 \(L_1\)。那么导线 1 受到的力矢量为： \[ \mathbf{F}_{12} = \frac{\mu_0 I_1 I_2}{4\pi} \frac{2}{D}(0, -1, 0)L_1.~ \] 正如预期的那样，导线受到的力与其长度成正比。单位长度上的力为： \[ \frac{\mathbf{F}_{12}}{L_1} = \frac{\mu_0 I_1 I_2}{2\pi D}(0, -1, 0)~ \] 力的方向沿 \(y\)-轴，这表示如果电流是平行的，导线 1 会被拉向导线 2。单位长度的力大小与上文给出的 \(\frac{F_m}{L}\) 表达式一致。

4. 著名推导

　　 按时间顺序排列：

5. 另见

6. 参考文献和注释

　　
1. "第 26 届 CGPM 决议" (PDF). BIPM. 检索于 2020 年 8 月 1 日。
2. Raymond A Serway & Jewett JW (2006). Serway 的物理学原理：基于微积分的文本 (第四版). 贝尔蒙特，加利福尼亚：汤普森 Brooks/Cole. 第 746 页. ISBN 0-534-49143-X。
3. Paul M. S. Monk (2004). 物理化学：理解我们的化学世界. 纽约：奇切斯特：Wiley. 第 16 页. ISBN 0-471-49181-0。
4. 此表达式的被积函数出现在关于定义安培的官方文档中。BIPM SI Units brochure, 8th Edition, 第 105 页。
5. Tai L. Chow (2006). 现代视角下的电磁理论导论. 波士顿：Jones and Bartlett. 第 153 页. ISBN 0-7637-3827-1。
6. 安培力定律。参见 “积分方程” 部分获取公式。
7. Christodoulides, C. (1988). “安培和毕奥-萨伐尔静磁力定律在线电流元形式中的比较”. 美国物理学杂志. 56 (4): 357–362. Bibcode:1988AmJPh..56..357C. doi:10.1119/1.15613。
8. O'Rahilly, Alfred (1965). 电磁理论. Dover. 第 104 页. (参见 Duhem, P. (1886). "关于安培定律". 理论物理学杂志. 5 (1): 26–29. doi:10.1051/jphystap:018860050020601. 检索于 2015 年 1 月 7 日，该文出现在 Duhem, Pierre Maurice Marie (1891). *电与磁的教程. 第 3 卷. 巴黎: Gauthier-Villars.)
9. Petsche, Hans-Joachim (2009). 赫尔曼·格拉斯曼传记. 巴塞尔波士顿：Birkhäuser. 第 39 页. ISBN 9783764388591。
10. Maxwell, James Clerk (1904). 电磁学教程. 牛津. 第 173 页。

7. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利