分子动理论(高中)
贡献者: pinganananan; addis
1. 分子动理论
对于分子的直观认识
当不需要区分分子、原子或者离子在化学变化中所起的作用不同时,而仅仅研究物体的热运动性质以及规律,可以将组成物体的微粒统称为分子。
我们不能直接观察分子,而必须借助高分辨率的显微镜,比如说扫描隧道显微镜1。这说明分子的尺度十分小,大概在 $10^{-10}\mathrm{m}$ 数量级。直观来感受的话,分子的大小比之于弹珠,则相当于一颗苹果与地球的体积相比拟。
与此同时,由于物质是由分子组成的,所以我们还能合理得到一个结论,即:在宏观尺度中,物质中所包含分子的数目很多,为 $10^{23}$ 数量级。事实上,$1\mathrm{mol}$ 的任何物质都含有相同的粒子数,这个数目为阿伏伽德罗常数,$N_A=6.02214076\times 10^{23}\mathrm{mol^{-1}}$。由于物体是由大量分子组成的,因此在后续我们研究中,认为体系均满足热力学极限2。
分子热运动
在生活中我们可以发现,不同种的物质能够相互进入彼此,这类现象叫做扩散。这种现象并非是由外力引起的,也即并非是由于重力作用、对流等造成,而是物质分子自身具有永不停息的无规则运动的体现,这种无规则的运动称之为布朗运动。
布朗运动最开始由英国植物学家布朗在显微镜下观察到,他发现悬浮在水中的花粉颗粒会进行移动,将其运动轨迹连接起来可以发现这样的运动是无规则的。布朗证明,这种移动并非由于花粉颗粒具有生命而产生。当花粉颗粒越小,则运动就越明显,这是由于花粉越小,单位时间内撞击花粉表面的水分子数目就越不平衡,另外,花粉越小,它的质量也就越小,运动状态就越容易发生改变,布朗运动也就越明显。
同样,升温也可以加剧花粉颗粒的运动。在扩散现象中,温度越高,扩散也就越快。由于这种分子运动和温度之间的密切相关关系,因此,我们将分子这种永不停息的无规则运动叫做热运动。温度是分子热运动剧烈程度的标志。
分子间作用力
通过对日常生活的观察,我们知道气体很容易被压缩,这是因为气体分子之间存在很大的空隙。而两种不同液体相互混合之后,总体积会小于原先单独体积的加和;紧紧压在一起的金块和铅块可以彼此渗透;这些现象说明,液体和固体的分子之间也存在着间隙。
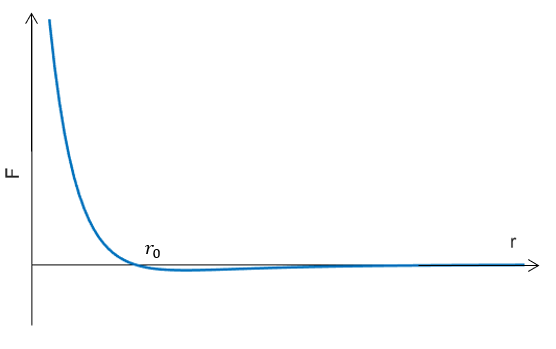
分子之间具有间隙,而非紧紧的挤压在一块,这说明分子之间存在排斥力;但是大量分子仍然可以聚集在一起形成物体,而没有散开,这说明分子之间存在引力。研究表明,分子之间的相互作用力 $F$ 和分子之间的距离 $r$ 关系如图所示:
当 $r< r_0$ 时,分子之间表现为排斥力;当 $r>r_0$ 时,分子之间表现为吸引力;而当 $r=r_0$ 时,分子之间作用力为 $0$,处于平衡位置。
分子间作用力是由于带电粒子的相互吸引所引起的,又称范德瓦尔斯力。后续我们将在原子物理中学习到范德瓦尔斯力更为详细的微观成因。
分子动理论
总结起来,分子动理论指的是通过研究微观粒子热运动来分析物质的热学性质和规律所建立的理论。其基本内容在上述段落中已经有所介绍,总结概括为以下三点:
- 物体是由大量分子组成的;
- 分子在做永不停息的无规则热运动;
- 分子之间存在这相互作用力;
这三点就是分子动理论的基本内容。人们利用分子动理论来对大量分子求统计平均,以此来建立宏观量和相应的微观量统计平均值之间的关系。我们将在下述对分子运动更进一步的分析中使用到分子动力学的观点。
2. 分子运动速率分布规律
由于分子运动是无规则的,所以在任一时刻,任何分子运动的方向和速率都具有偶然性,与此同时,所要研究的对象又包含极其大量的分子,因此我们无法通过详细求解每一个分子的运动状态来得到整体的性质。但是大量随机事件的整体往往会表现出一定的规律性,满足统计规律,大量分子的整体运动也不例外,我们将从这个角度出发,来分析分子运动的一般规律。
气体分子运动的特点
和固体与液体相比,气体分子之间的距离很大,而且分子的大小相对于分子间距很小,因此可以将气体分子视作质点,另一方面,由于气体分子间距很大,因此分子间相互作用力很弱,所以可以认为气体分子运动状态的改变来源于气体分子的相互碰撞和与器壁的碰撞,而在不受力的时候做匀速直线运动。
但是根据我们之前的叙述,组成宏观物体的气体分子数目仍然十分巨大,无法通过分析每一个分子的运动来得到整体的性质,所以只能通过统计的方法来对分子运动进行分析。合理推知,由于分子的数密度很大、分子间碰撞频繁,所以在某一时刻时朝各个方向运动的分子数目应该几乎相等,在空间上是均匀的,满足平移对称性。
分子运动速率分布图像
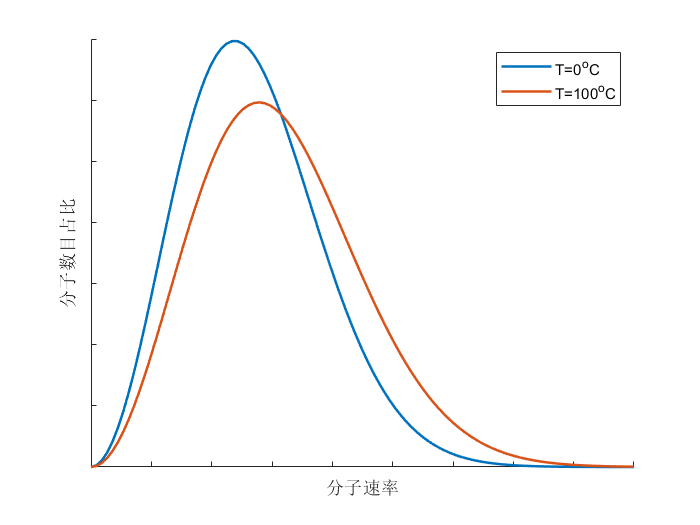
当我们考虑大量分子的运动速率时,可以发现其服从一定的分布规律,定性的示意图可以绘制如下:
从图中可以看出,某一温度下的气体,分子的运动速率都是 “中间大、两头小” 的,即运动速率特别大和特别小的分子数目都相对较少,这也符合我们统计学的常识。而将不同温度的气体运动速率进行比较,可以发现温度高的气体,其分子运动速率相对较快,具有最大比例的运动速率区间表现为高温大于低温,这也是” 温度越高,分子热运动越剧烈” 的体现。
气体压强的微观解释
气体对容器具有压强,从分子动理论的角度来看,这个压强来源于分子的热运动。当气体分子随机的和容器壁发生碰撞时,由于其动量的改变,会对容器壁产生作用力。考虑大量气体的影响则产生了压强,由于分子的数目足够多,所以在任意时刻碰撞到容器壁的分子给予容器壁的力差不多,因此压强可以看作是不变的。
稍作说明,如果将气体分子和容器壁的碰撞视为弹性碰撞,气体分子碰撞前动量为 $mv$,碰撞后为 $-mv$,则在碰撞过程中,气体分子受到的冲量为 $$F\Delta t=-mv-(mv)=-2mv~,$$ 受到的作用力则为 $$F=-\dfrac{2mv}{\Delta t}~.$$ 根据牛顿第三定律,这单个分子对容器壁产生的力为 $$F^\prime=-F=\dfrac{2mv}{\Delta t}~,$$ 如果将大量分子的撞击都考虑进去,则可以得到容器壁所受的压强。
由上述说明可知,容器受到气体的压强主要受两个方面的影响:
- 容器中气体分子的数密度;
- 容器中气体分子运动的平均速率;
可知,容器中气体分子的数密度越大,则单位时间内和容器壁碰撞的气体分子数目就越多,容器壁受到的平均作用力就越大;而容器中气体分子运动的平均速率越大,则每次碰撞改变的动量就越多,容器壁所受到的平均作用力也越大。
3. 分子动能和分子势能
分子动能
我们知道,分子在永不停息的做无规则热运动,所以分子具有动能。在对于热现象的研究中,我们关心大量分子集体表现出来的热学性质,因此,这里重要的是所有分子动能的平均值,也叫作分子热运动的平均动能。
和普通物体的物理规律一样,在温度升高时,由于分子热运动加剧,平均速度更快,因此平均动能也越大,温度越低时则越小。由此,我们可以从分子动力学的角度理解温度的微观含义。
分子势能
分子间也存在着势能,其大小由分子间的相对位置决定。由图 4 所示,当分子之间的距离是无穷大时,可以规定分子间的势能为 $0$,而分子距离无限小的时候,排斥力会非常大,分子间势能也将非常大。实际上,势能对距离求导可以得到分子间的作用力,因此在图中我们可以看到,当分子间作用力等于 $0$,也即分子处于平衡位置时,分子间的势能达到最小值。 需要指出,分子间的作用力是保守力,也即做功和路径无关。当物体的体积变化时,分子间的距离将随之发生改变,因此会改变分子的势能。
物体的内能
由上可知,温度和体积的改变分别可以通过影响分子的平均动能和平均势能的方式来改变大量分子所具有的能量。我们将物体中所有分子的热运动动能与分子势能的总和叫做物体的内能。内能是所有物体都具有的。
需要提醒注意的是,内能可以理解为 “物体内在固有的某种能量”,当物体作为整体进行运动时,比如说具有速度或者具有高度,这时候的动能和势能是由物体的机械运动决定的,是机械能的一部分,对物体本身的内容没有贡献。
1. ^ 扫描隧道显微镜是一种可以个探测物质表面结构的仪器。其工作原理是利用探针和物质表面的相互作用来获得物质表面结构的图像信息,分辨尺度为原子尺度。
2. ^ 热力学极限是指粒子数(或者体积)趋近于无限大时的极限。