Minimax 搜索和 Alpha-Beta 剪枝

                     

贡献者： int256

　　 本文中，使用孩子节点表示在树中、深度仅更深一层，并且与其直接相邻的节点（也就是进行深度优先搜索过程中在当前节点下，再向下搜索一层可以达到的节点）。使用叶子节点表示最深一层节点。

1. Minimax 搜索（极小化极大搜索）

　　 首先值得提出的一点，这个搜索算法并不适用于围棋的布局、中盘等局面，更适合末期或象棋（对于前期也不是很适合，尤其是分支有很多的时候）或 Tick-Tack-Toe（井字棋）等，读者可以在学习完本文后思考其原因。

　　 在双方博弈类型的搜索中，例如棋类的最优化搜索，如果我们是 AI，我们会希望，走下这一步棋后，我们的最大的失败可能最小。为什么这里是 “最大的失败可能” 而失败可能不是一个定值呢？因为对方的可能下法不止一种，对于每一种对方的下法，我们也都有一个 “失败的可能性”（实际上这里是一个最小值，我们选择下最优的下法让我们失败的可能性最小），我们需要使用这些失败的可能性的总体的最大值来评估这步棋的好坏。

　　 所以可以发现，这是一个使得某个最大值（失败的可能性）最小的算法，所以叫做极小化极大搜索（Minimax 搜索）。有的地方也叫做 Minmax 搜索。

　　 那么实际上搜索进行的是，” 你一步我一步 “的方法。也就是，循环以下过程：

  1. AI（“我”）先选择最优的方法下棋；
  2. 对方（“你”）再选对于你来说最优、也就是对我来说最差的一个方法下棋。

　　 考虑一个经过一些常规剪枝技巧的、搜索树为二叉树的对弈。我们模拟搜索并且步骤也遵循递归的步骤，通过模拟的过程来学习 Minimax 搜索方法。

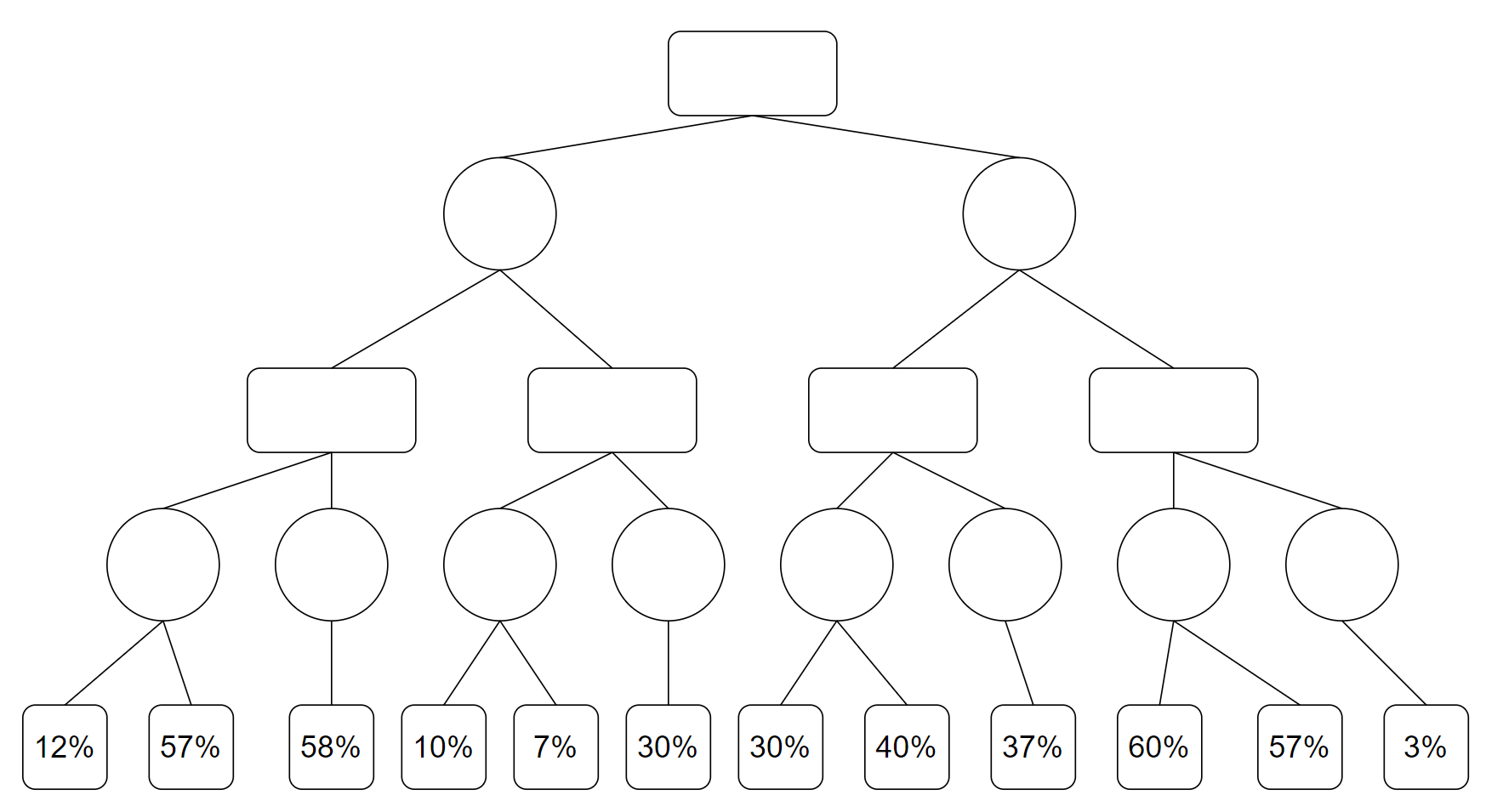
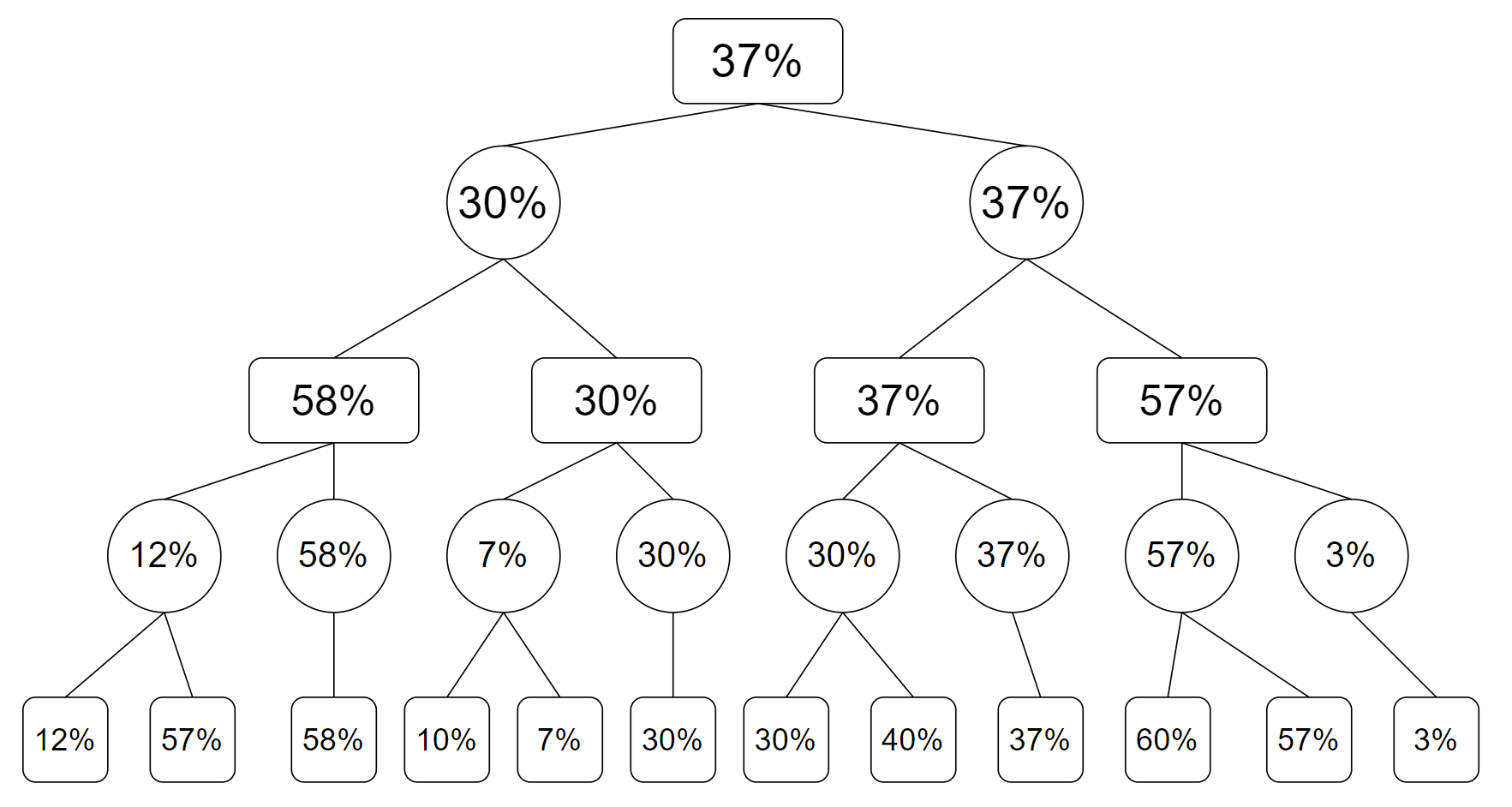
　　 假若现在应当 AI 下棋，我们向后搜索 $4$ 步棋，绘制出搜索树并且标出叶子节点的一个 “估价”（也就是 AI，“我”，的胜率）：

图
图 1：模拟搜索树（仅叶子节点）

　　 其中，圆角方框为 AI 需要下棋，圆形为对方需要下棋。

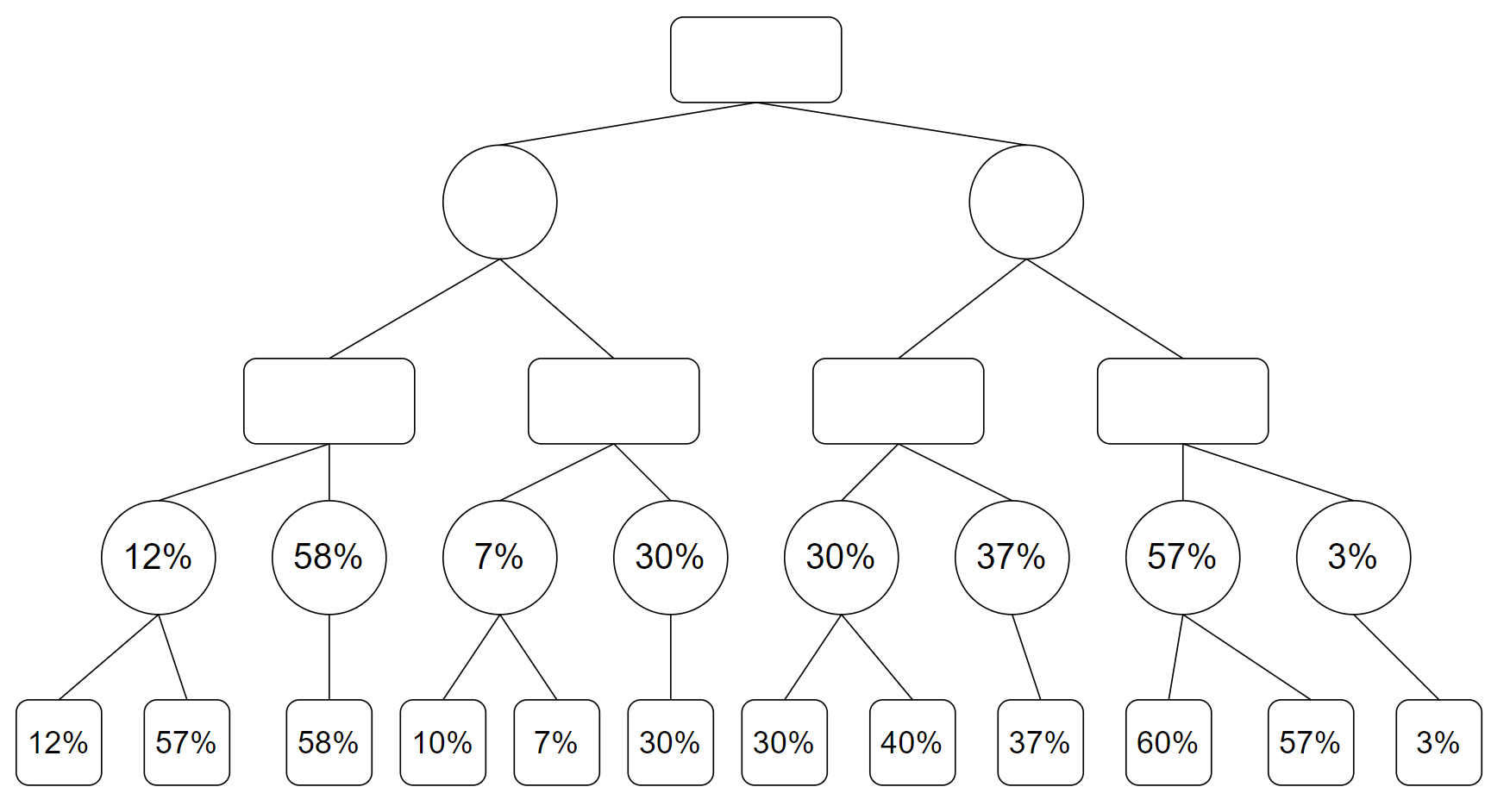
　　 那么，在对方下棋（也就是圆形的节点）进行搜索的时候，对方如果是 “足够聪明的”，会选择让我们的胜率最小，也就是失败率最大的下法。也就是对所有这些可能胜率求最小值，模拟搜索过程进行更新后得到新的搜索树：

图
图 2：模拟搜索树（更新一层后）

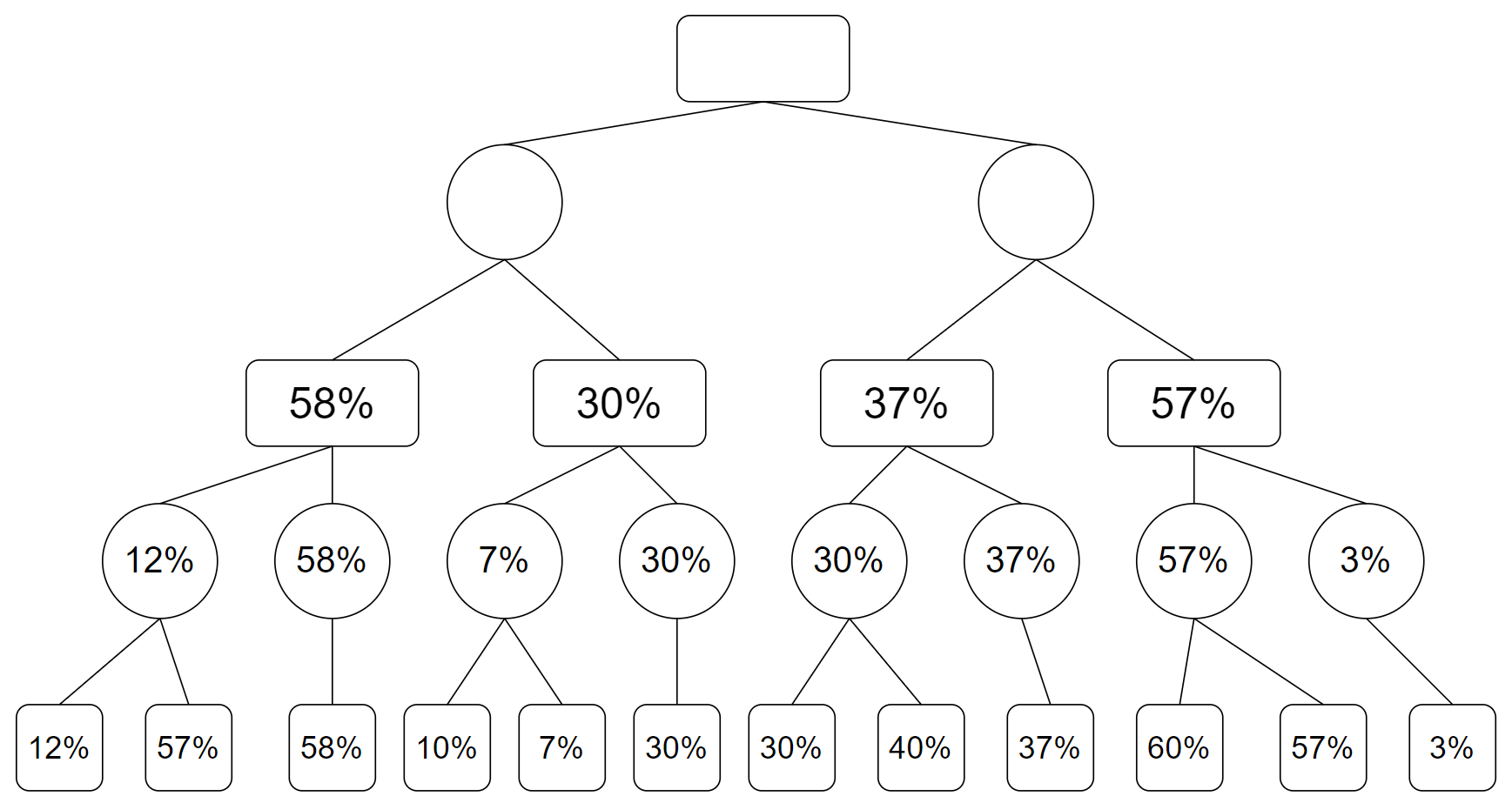
　　 之后向上一步，轮到 AI 下棋，AI 会选择使自己胜率最大的，也就是对所有可能胜率求最大值，这次更新后为：

图
图 3：模拟搜索树（更新两层后）

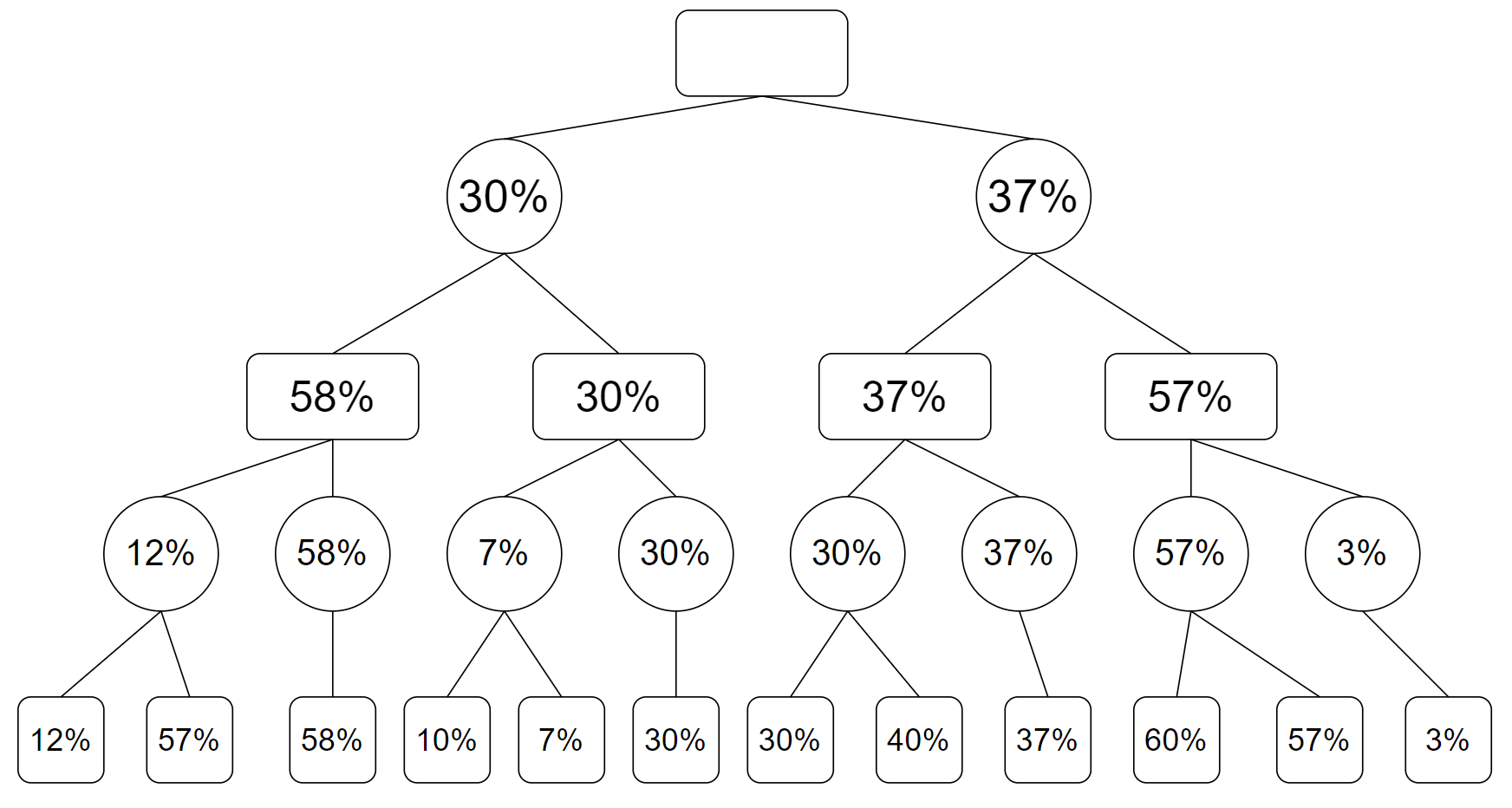
　　 现在这轮，又轮到对方下棋，对方这时候下棋仍然会选择使我们胜率最低的下法，也就是求最小值，这一次更新后的搜索树为：

图
图 4：模拟搜索树（更新三层后）

　　 最后回到了搜索的根节点，这一步是 AI 下棋，选择使得自己胜率最大的方法下棋，也就是对所有这些胜率求最大值，得到最终的搜索树：

图
图 5：模拟搜索树（最终，仅更新胜率）

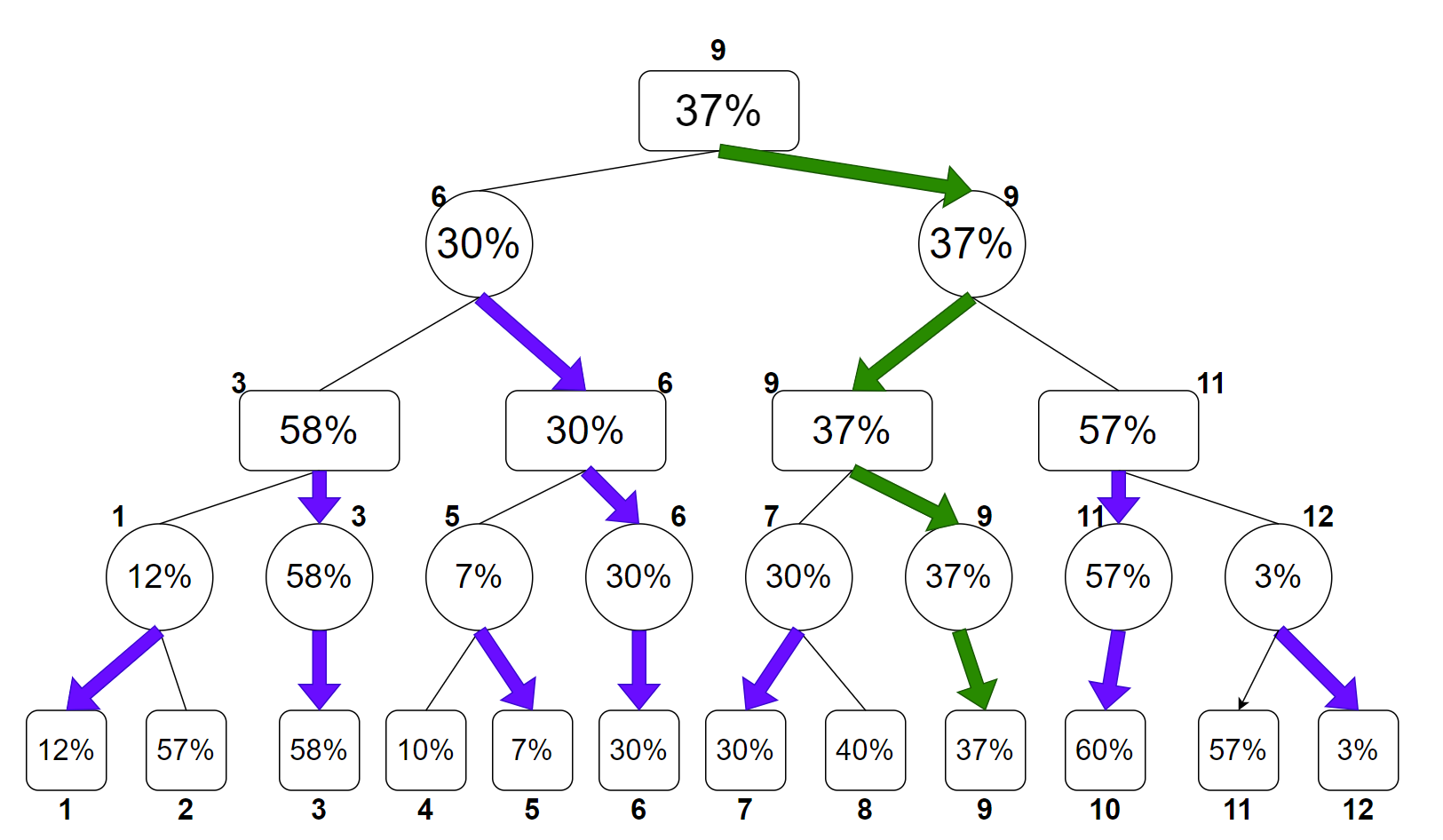
　　 这就是朴素 Minimax 算法的搜索过程，当然实际搜索还会记录路径信息，也就是我们这一步棋要如何下。带更新路径信息的搜索树如下：

图
图 6：带记录路径信息的搜索树（最终形态）

　　 其中，绿色路径为最终选择路径，紫色为该节点可以选择的、这个节点该下棋的一方可以选择的最优下法。

　　 需要注意的是，实际情况中，搜索不是一层一层进行的，而是按递归的顺序（节点本身-左孩子到右孩子-节点本身-回溯）进行遍历的。

　　 不难发现，我们在交替取 min 和 max，同时记录这最大（小）值是从哪个孩子节点回溯来的，于是可以写出 Minimax 搜索的朴素方法的代码： 

int MiniMax(int dep); 
int Evaluate(); // 计算当前棋盘我方胜率情况 
void genMoves(); // 生成走法 
bool nxtMove(); // 选择下一个走法，并返回是否还有走法 
void doMove(); //  走这步棋 
void undoMove(); // 撤销这步棋（回溯）
int getMoveID(); // 获取这步棋走法的 ID 
int trueMoveID; // 最终选择的走法的 ID 

int MiniMax(int dep) {
	int best = -101;
	// 初始最大胜率赋值为一个极大负值，后面求最大值会更新掉 
	
	if(dep <= 0) return Evaluate(); 
	
	genMoves();
	int score; // 当前最优胜率 
	while(nxtMove()) {
		doMove();
		score = -MiniMax(dep - 1);		
		undoMove();
		if(score > best) {
			trueMoveID = getMoveID();
			best = score;
		}
	}
	return best;
}
这里用到了一个 trick（代码技巧）叫做负值最大算法，搜索过程中通过将当前分数记录为相反数便可以一直使用最大值来更新最高胜率。（敌方胜率的相反数最大，即敌方胜率最小，也就是我方胜率最大。）

2. Alpha-Beta 剪枝

　　 Alpha-Beta 剪枝是这类搜索的一个常用技巧，其中 Alpha（$\alpha$）表示目前所有可能解中的最大下界，Beta（$\beta$）表示目前所有可能解中的最小上界。

　　 我们来观测一个一共 $3$ 层的搜索树（算上根节点），并在模拟一部分搜索的过程中了解 Alpha-Beta 剪枝的原理。

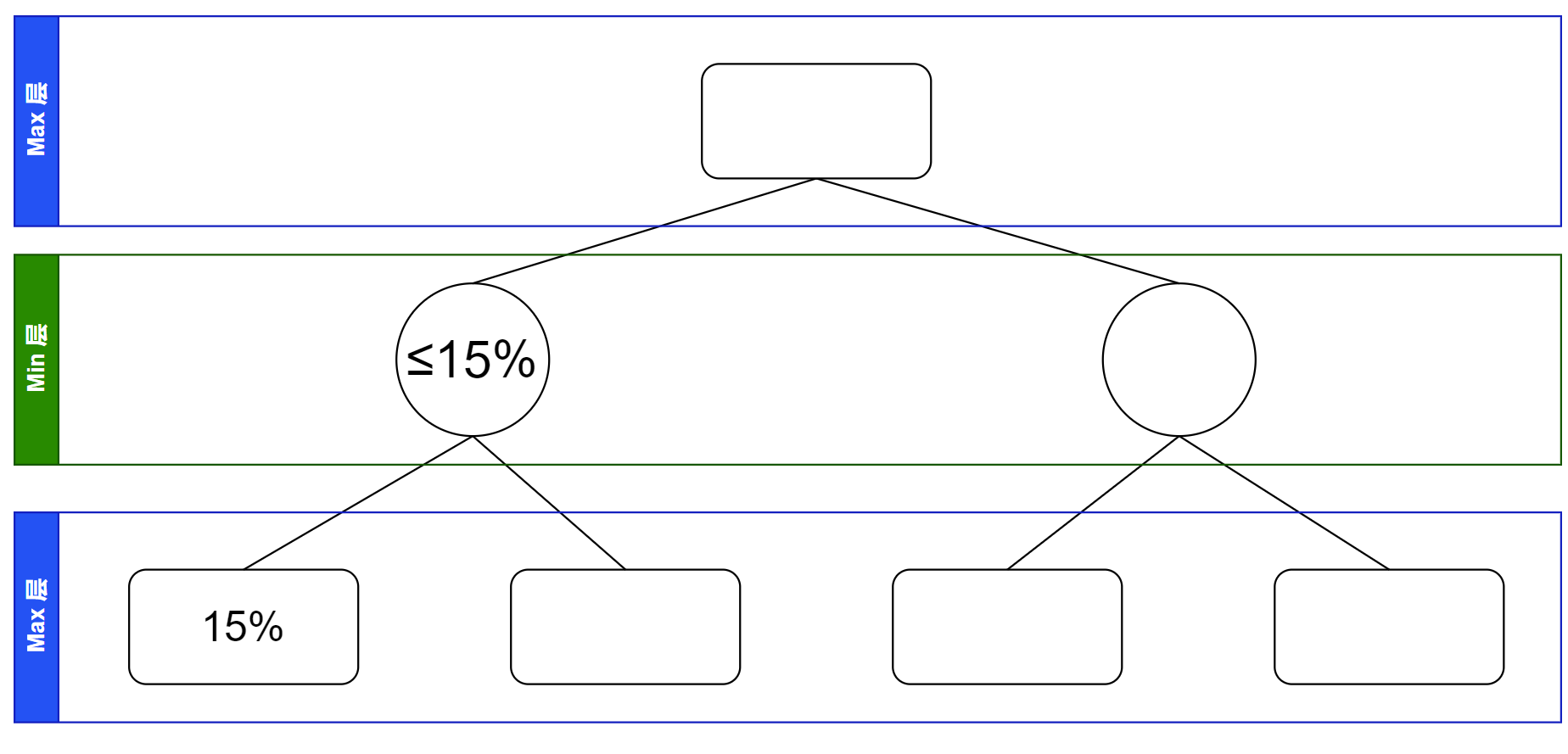
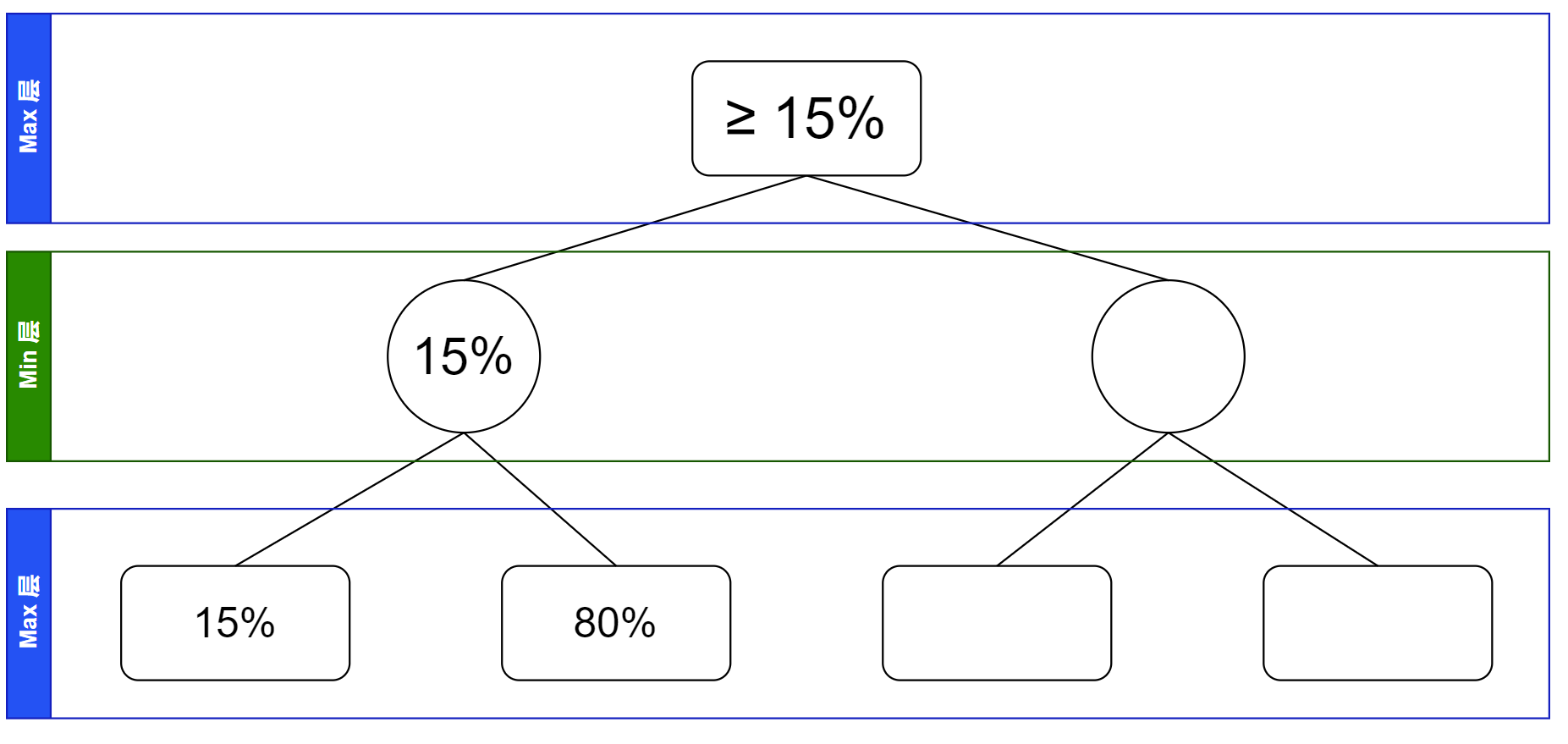
　　 首先搜索到第一个叶子节点，假若这处计算出胜率为 $15\%$，那么他的父亲结点是对所有孩子求最小值，所以一定 $\le 15\%$。可以记录并画出模拟搜索树如下图。

图
图 7：搜索到第一个叶子节点的模拟搜索树

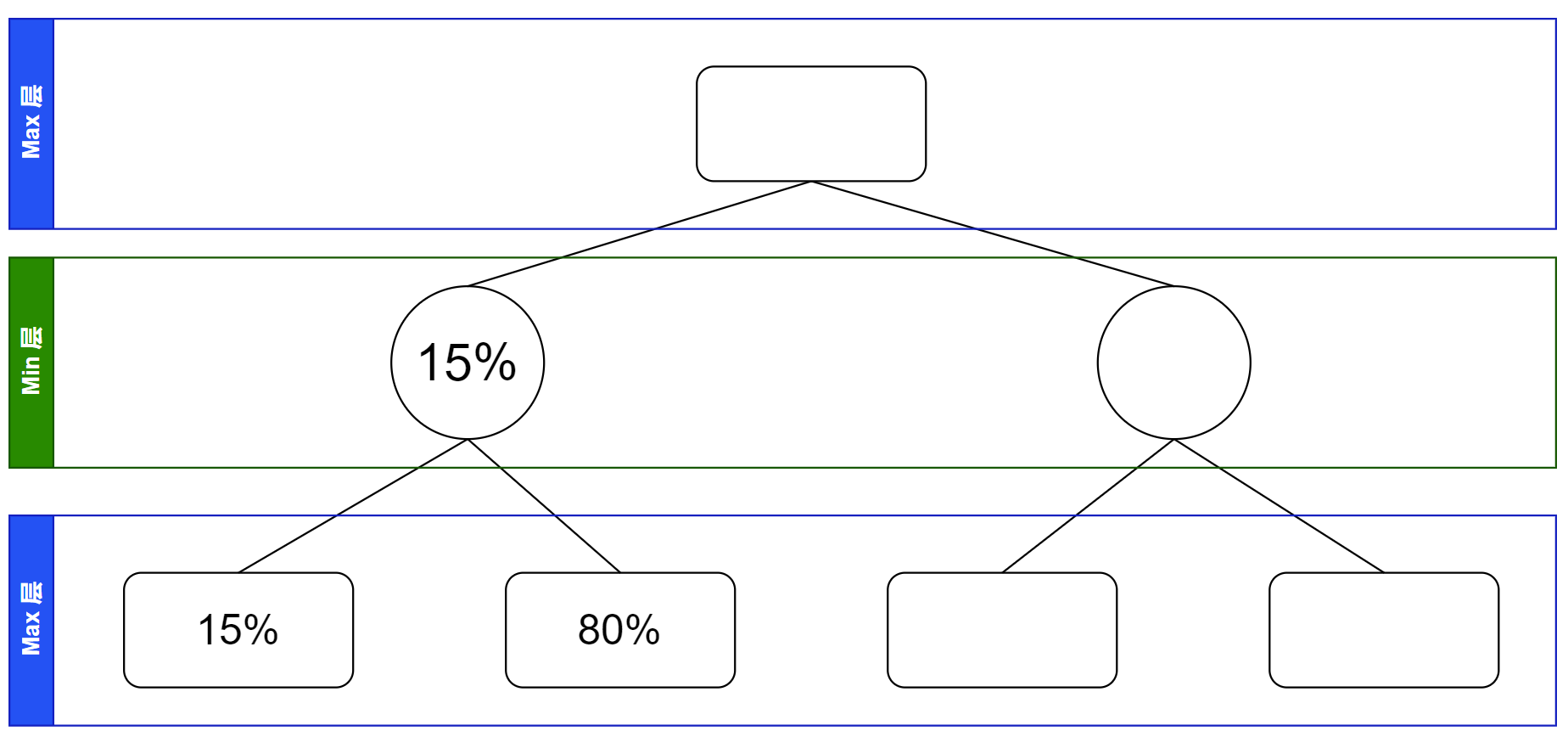
　　 接下来搜索到下一个叶子节点，假若这处计算出胜率为 $80\%$，则这两个叶子节点的父亲节点的值也可以确定了。在不考虑更新 “各节点的取值范围” 的前提下先绘制出模拟搜索树如下。

图
图 8：搜索到第二个叶子节点的模拟搜索树

　　 可以发现，这个时候可以确定根节点的值应当是 $\ge 15\%$ 的，所以可以记录下来这个信息，同时这将帮助剩余部分的搜索。

图
图 9：记录根节点取值范围信息

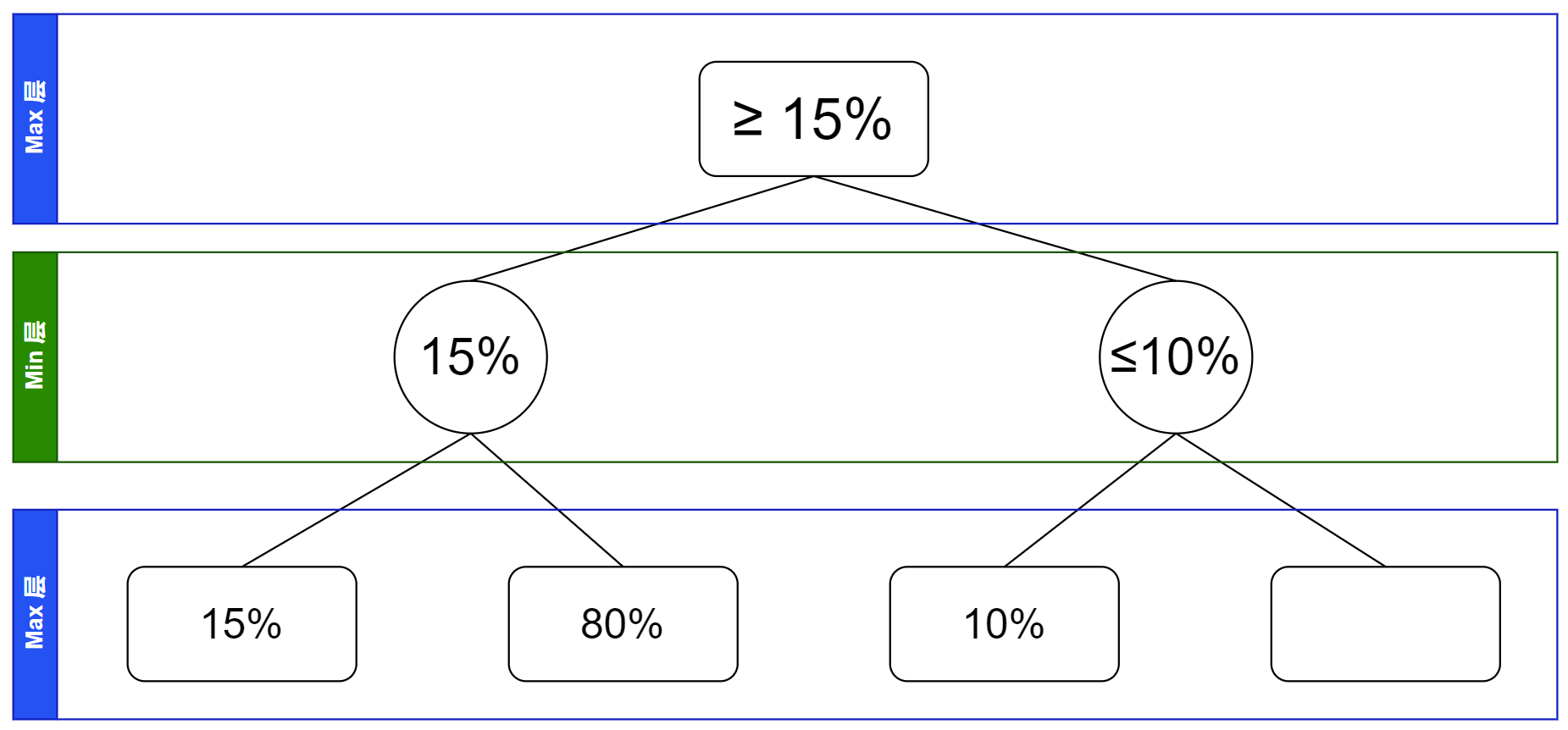
　　 接下来仍按递归的顺序进行搜索，轮到搜索第三个叶子节点了。假若这处计算出胜率为 $10\%$，那么他父亲结点的值就一定是 $\le 10\%$ 的，可以画出下图。

图
图 10：搜索到第三个叶子节点的模拟搜索树

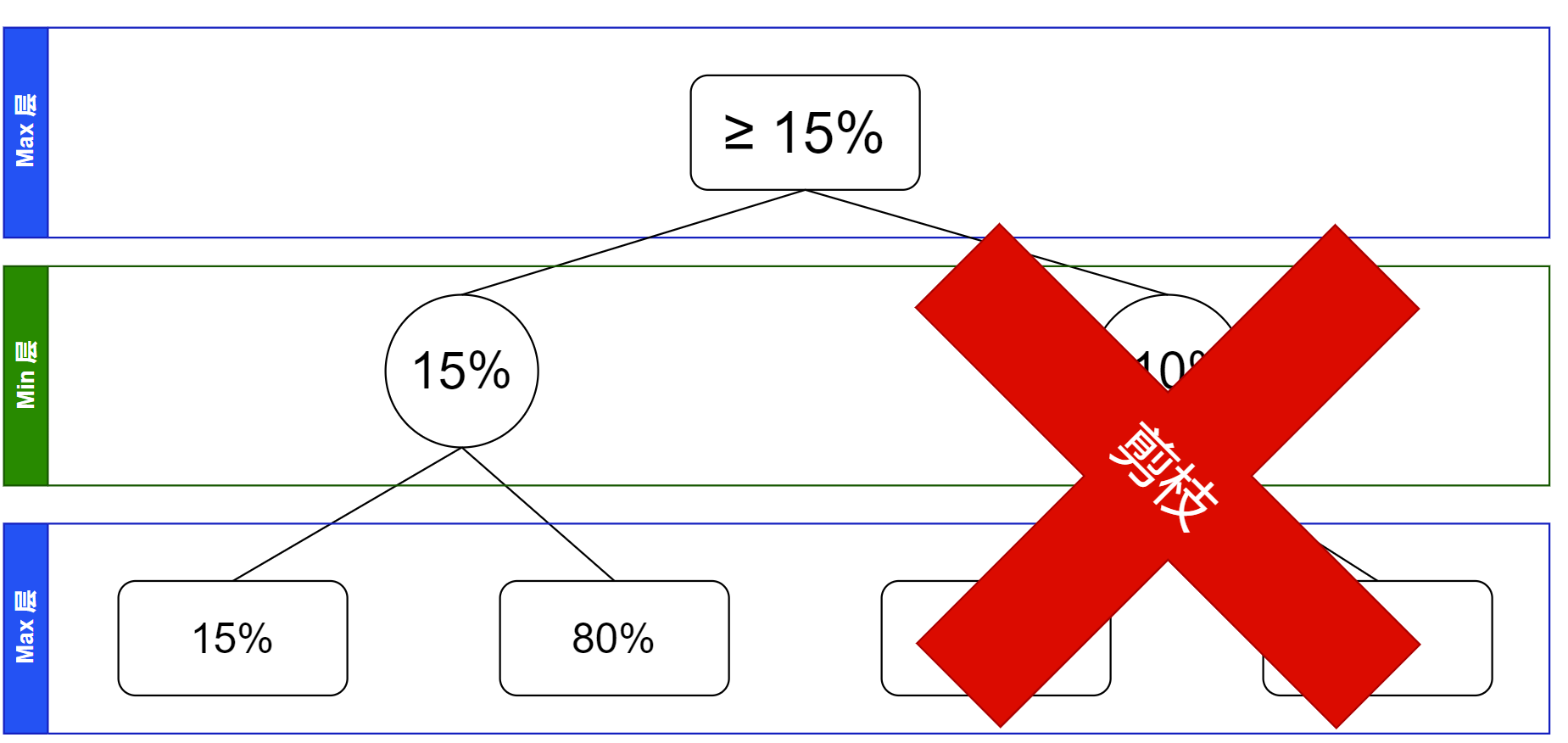
　　 我们发现，根节点是对所有其孩子节点求最大值，但当前这节点的取值范围的最大值小于了根节点的取值范围的最小值，所以无论怎样根节点都不会取这个节点的值了。那么这个节点的整个子树都可以剪枝掉，如图。

图
图 11：剪枝后的模拟搜索树

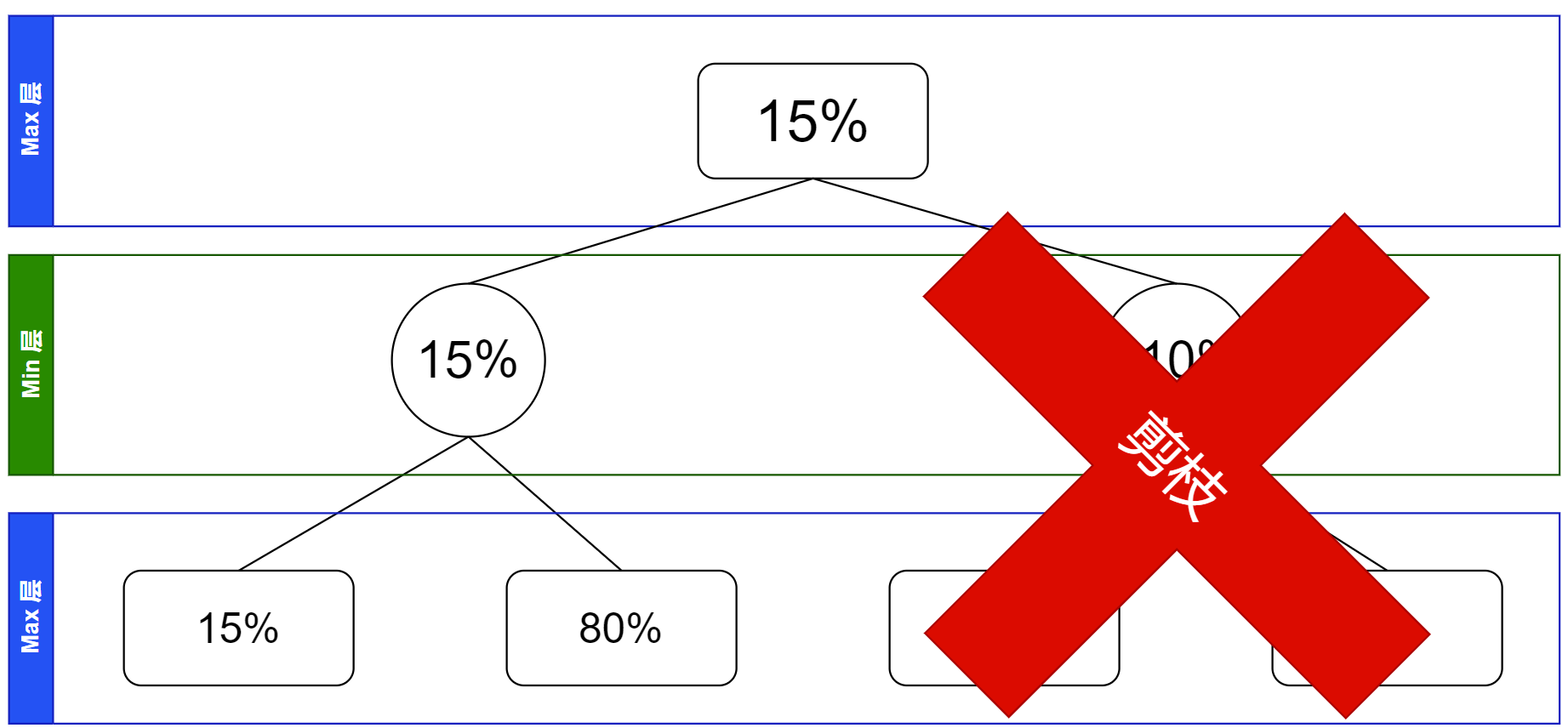
　　 于是也就可以确定根节点的值是 $15\%$，完成了搜索。

图
图 12：模拟搜索树最终形态

　　 这个过程其实就是一个形象的 $\alpha-\beta$ 剪枝，也就是当一个节点的取值范围偏离，使得他不会对父亲节点的最终结果有贡献的时候，把这偏离的节点的整个子树都剪枝。

剪枝原理

　　 首先，引入 $\alpha$ 和 $\beta$ 两个值：

　　 $\alpha$：我方节点能取得的最小值（极大节点的下界）。

　　 $\beta$：对方节点能取得的最大值（极小节点的上界）。

　　 每个节点都会有其 $\alpha$ 值和 $\beta$ 值，这可能是已经搜索过的子树贡献来的，也可能是从父节点第一次搜索时继承来的。 这个继承的目的是为了每次节点可以直接使用自己的值，而不对父亲节点产生影响。例如图 10 中在第一次访问到根节点的右孩子（而非回溯过程）的时候，它就会有一个从根节点继承来的 $\alpha = 15\%$。叶子节点不继承 $\alpha$、$\beta$ 信息，仅对父节点贡献信息。

　　 那么显然，一个节点及其子树要被剪枝会发生在其 $\alpha \ge \beta$ 的前提下。这会使得他对父亲节点的最终值没有贡献。

　　 为此重新绘制一个包含 $\alpha$、$\beta$ 信息记录的搜索树并再次给出模拟的搜索过程，以便理解。 在这搜索过程中，节点空白表示还没有访问过，一旦访问过就会记录信息，初始的 $\alpha$、$\beta$ 值是直接从父节点继承（直接复制）来的。 蓝色节点表示当前正在访问的节点，红色箭头表示回溯过程并传递子节点信息、更新父节点的 $\alpha$ 与 $\beta$ 值，绿色箭头是搜索路径。

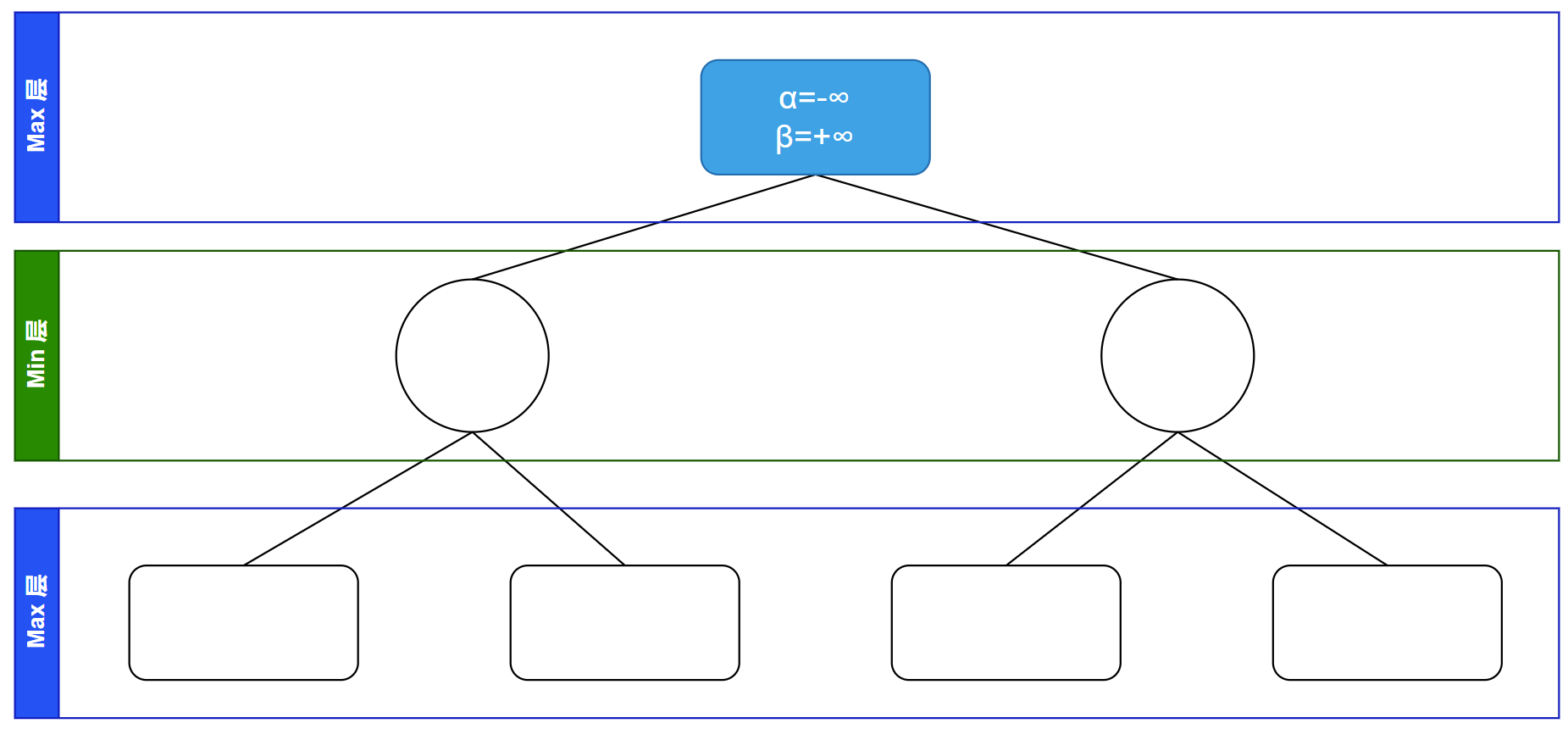
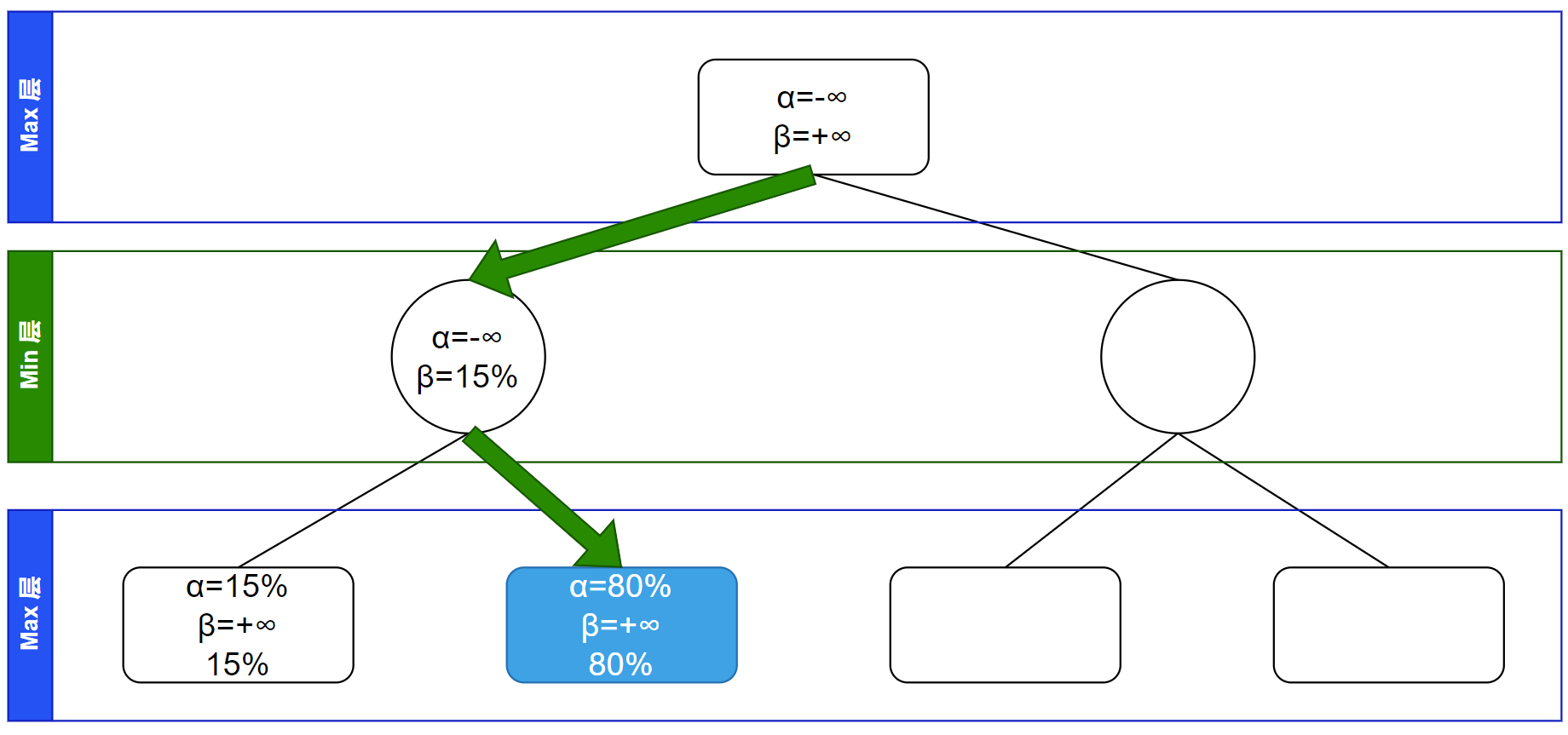
　　 最开始的时候搜索递归访问到根节点，初始 $\alpha$、$\beta$ 值：

图
图 13：步骤 $1$

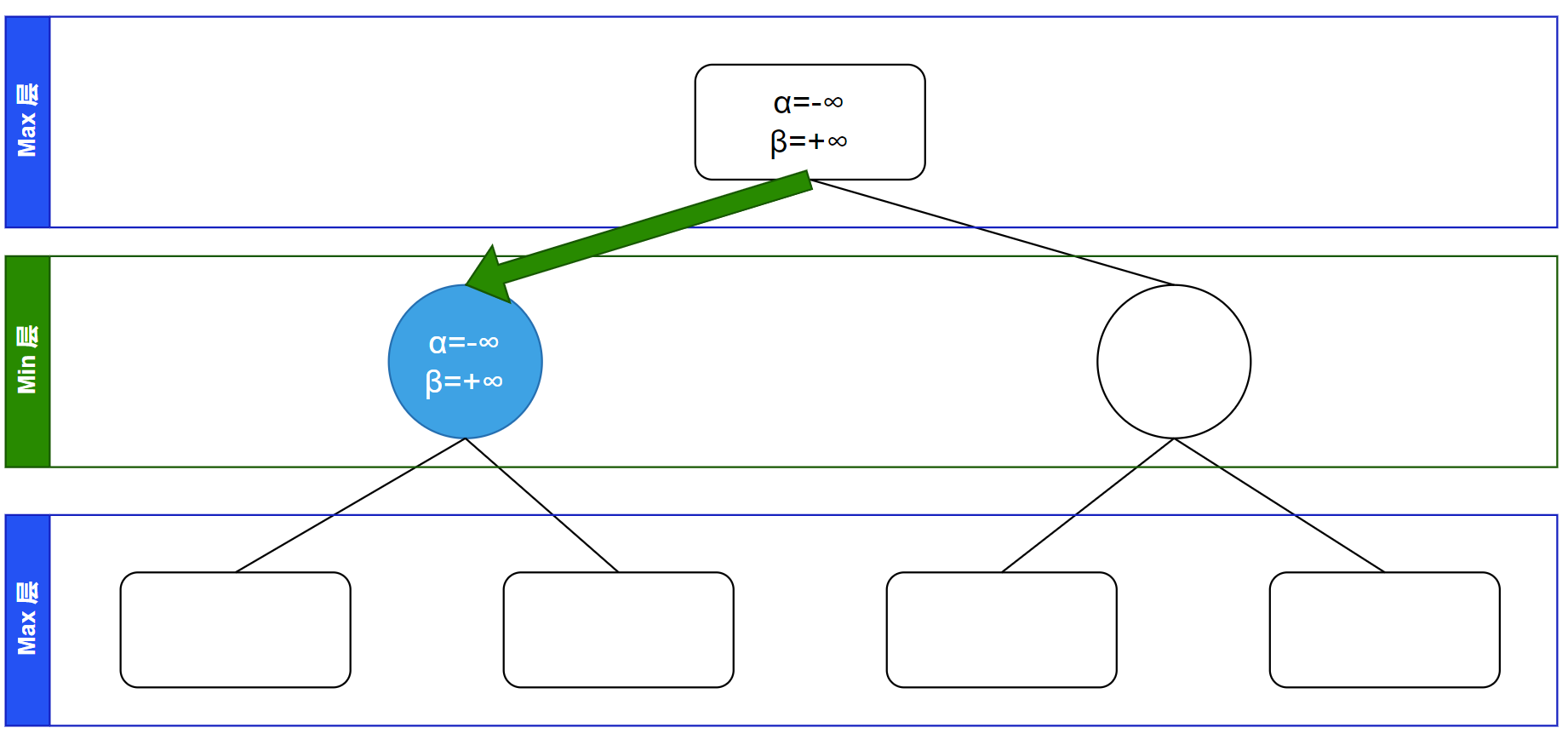
　　 接下来递归访问到最左侧孩子节点，继承其父亲结点的 $\alpha$、$\beta$ 值（直接复制）：

图
图 14：步骤 $2$

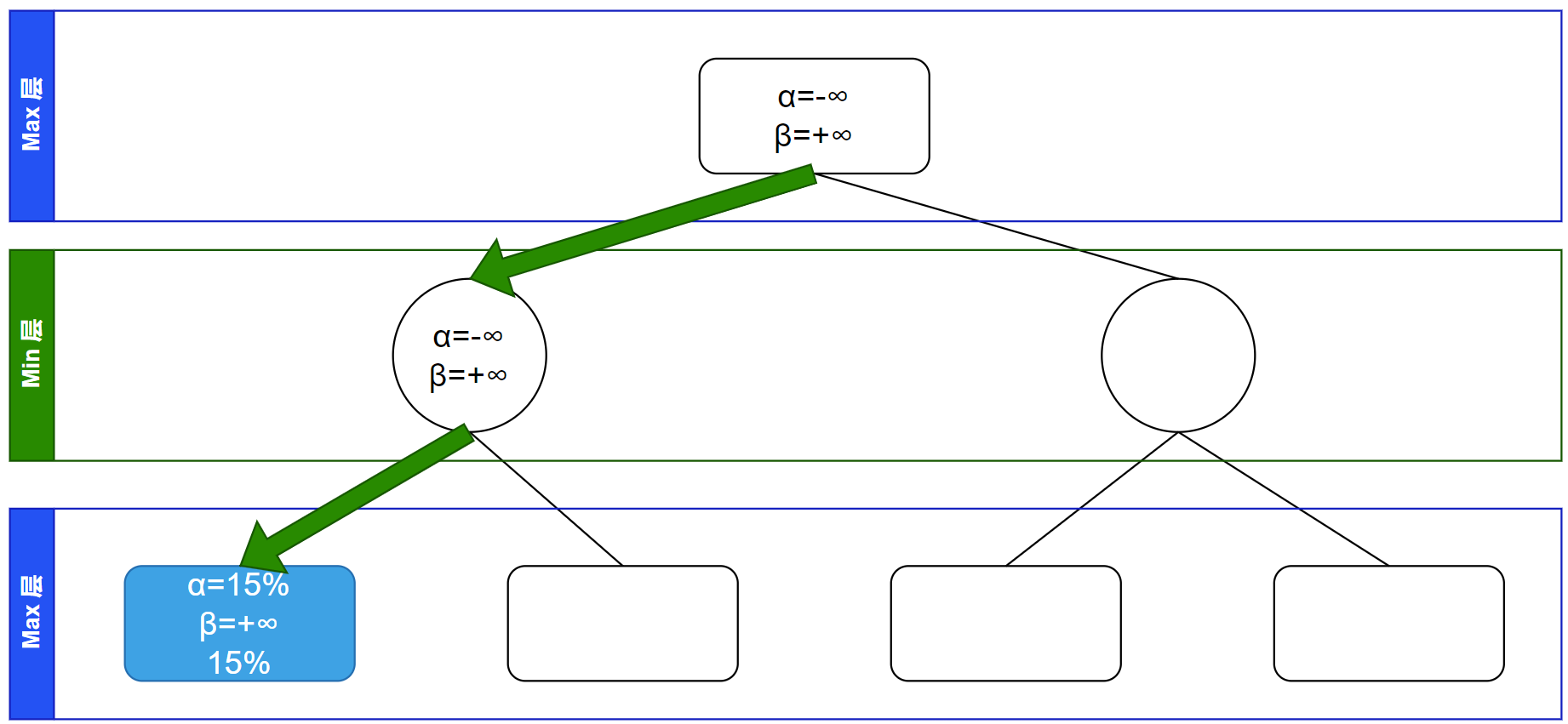
　　 继续递归，访问到第一个叶子节点，叶子节点不继承信息、仅自更新其自己 $\alpha$、$\beta$ 信息。由于是 Max 层，更新 $\alpha$ 信息：

图
图 15：步骤 $3$

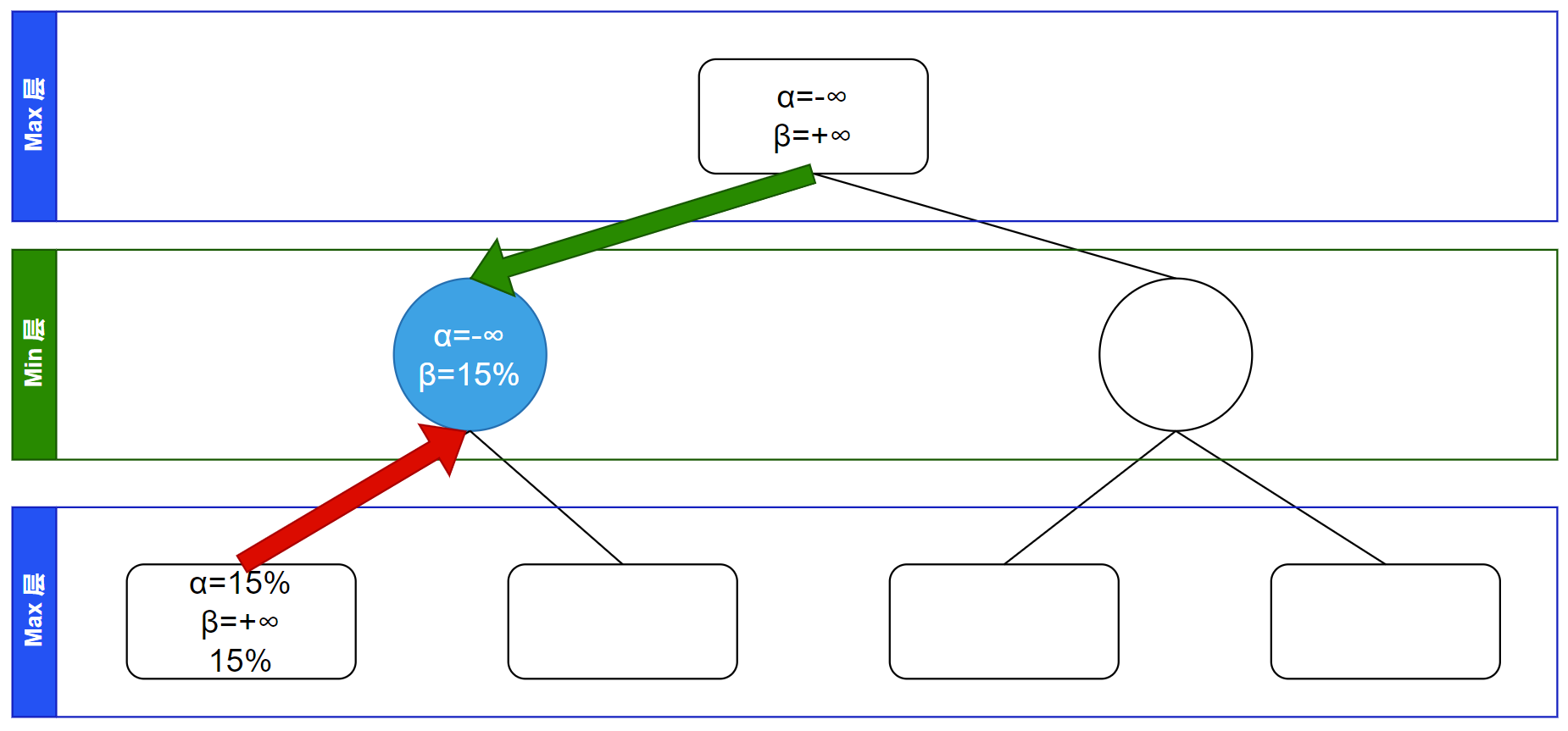
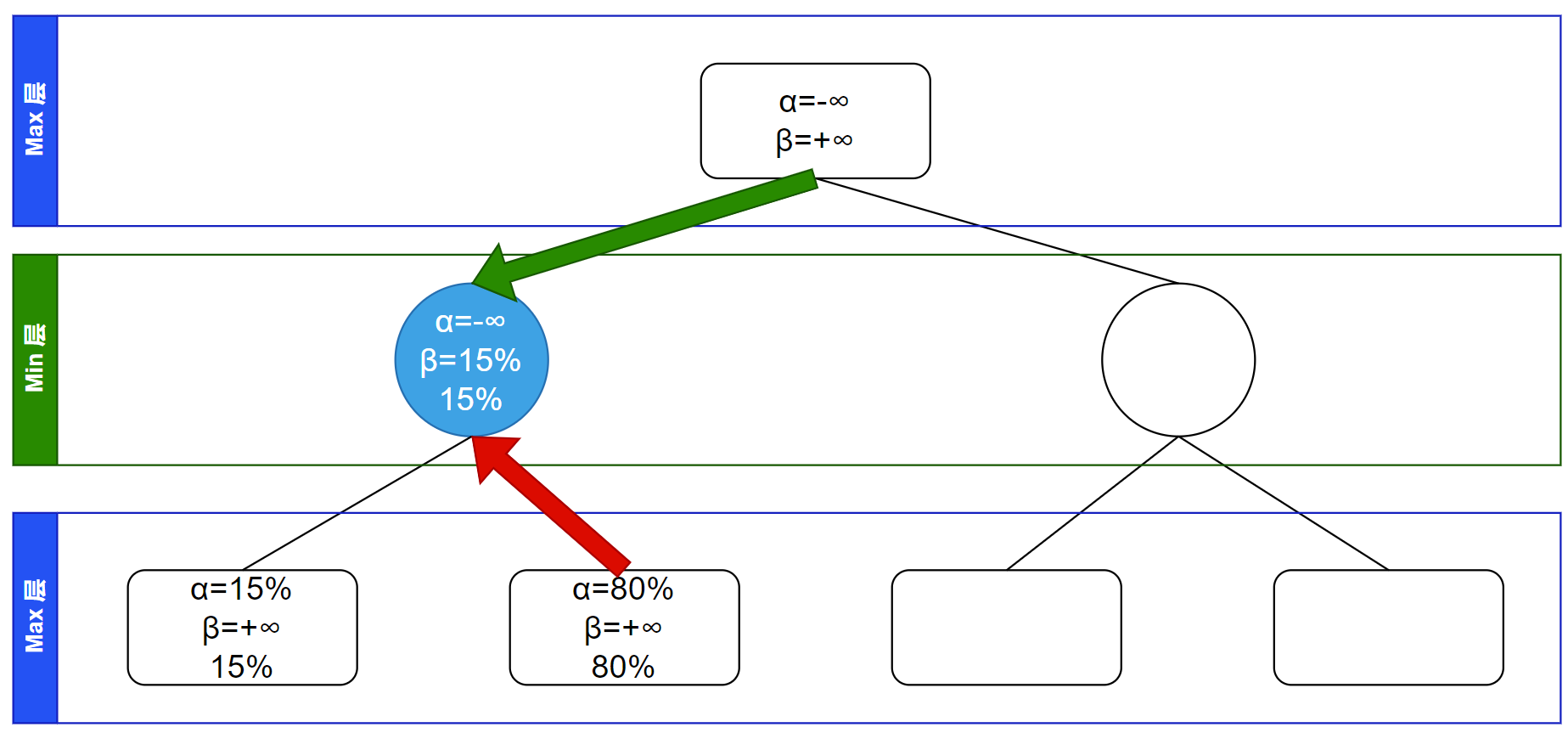
　　 这条搜索到底，向前回溯，回溯过程中传递孩子节点信息给父亲并更新父亲节点的 $\alpha$、$\beta$ 信息。因为父节点在 Min 层，所以更新 $\beta$ 信息：

图
图 16：步骤 $4$

　　 之后继续递归搜索，轮到下一个叶子节点，仍然不考虑继承、仅自更新 $\alpha$、$\beta$ 信息。因为是在 Max 层所以更新自己的 $\alpha$ 信息。

图
图 17：步骤 $5$

　　 回溯，在 Min 层所以更新 $\beta$ 值（$\beta$ 值取各子节点的所有 $\alpha$、$\beta$ 值的最小值）。此时访问完该节点的所有子节点，同时可以计算出胜率信息并记录：

图
图 18：步骤 $6$

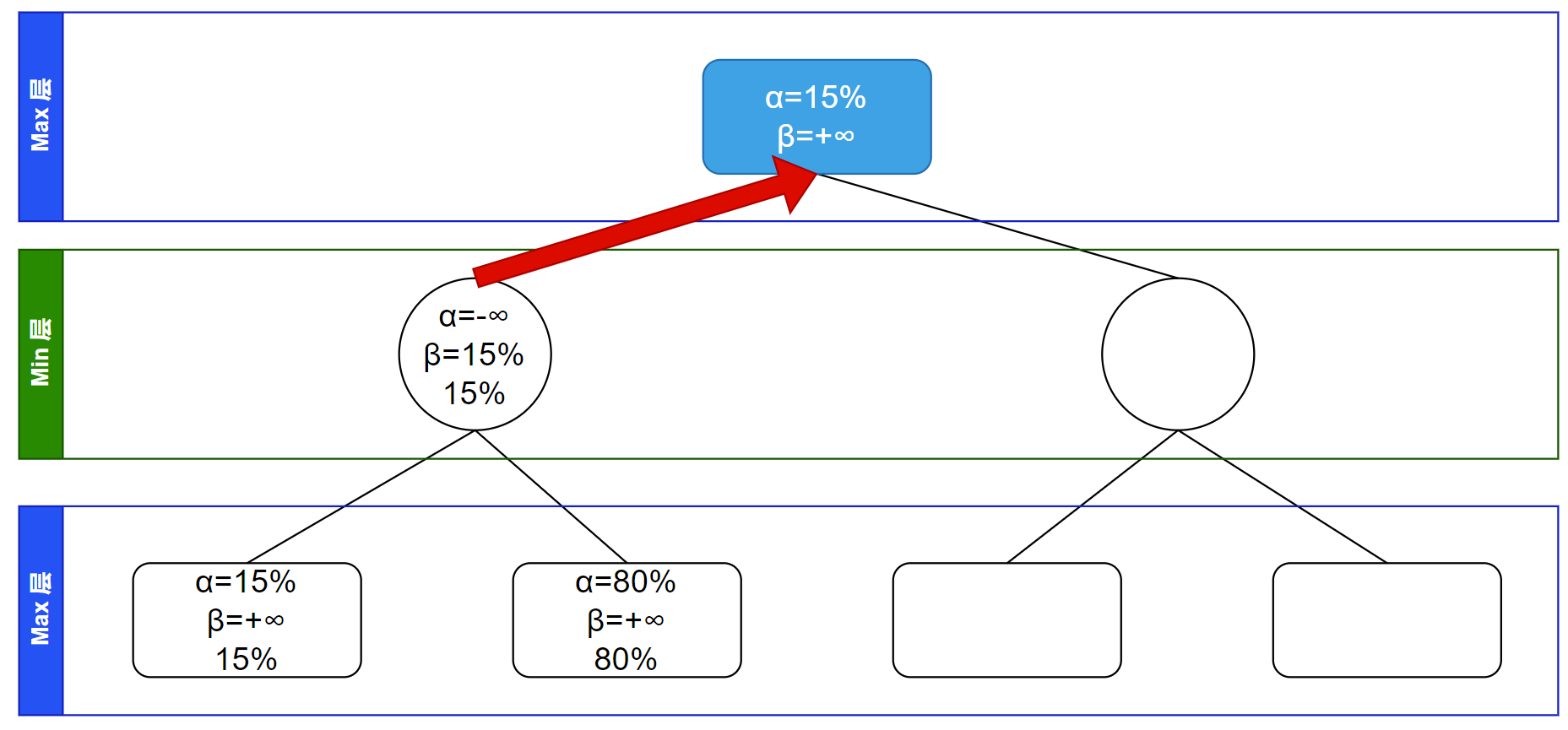
　　 继续回溯，回溯到了根节点，因为在 Max 层所以更新 $\alpha$ 值（$\alpha$ 值取各子节点的所有 $\alpha$、$\beta$ 值的最大值）：

图
图 19：步骤 $7$

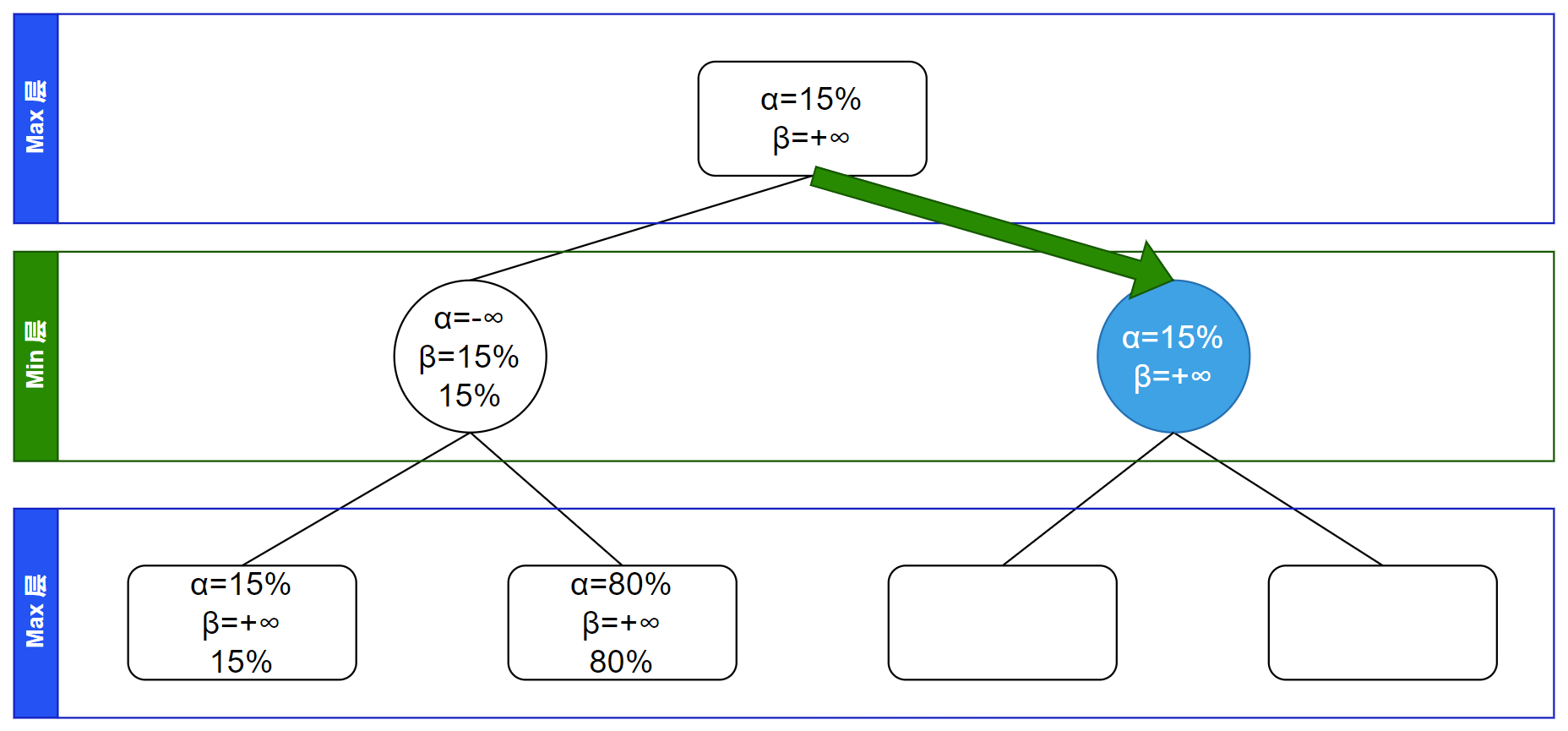
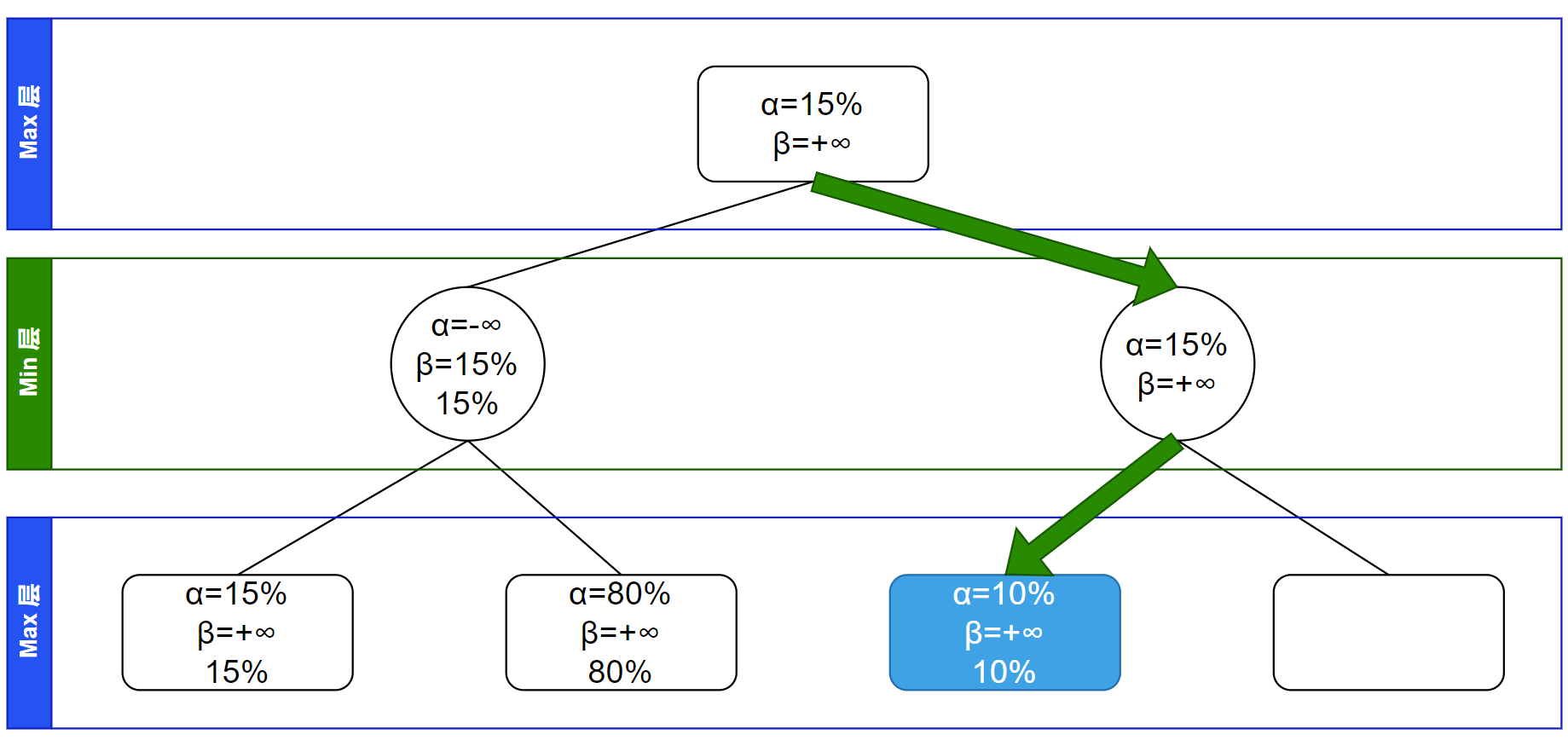
　　 接下来继续搜索，该递归访问根节点的下一子节点，继承 $\alpha$、$\beta$ 信息：

图
图 20：步骤 $8$

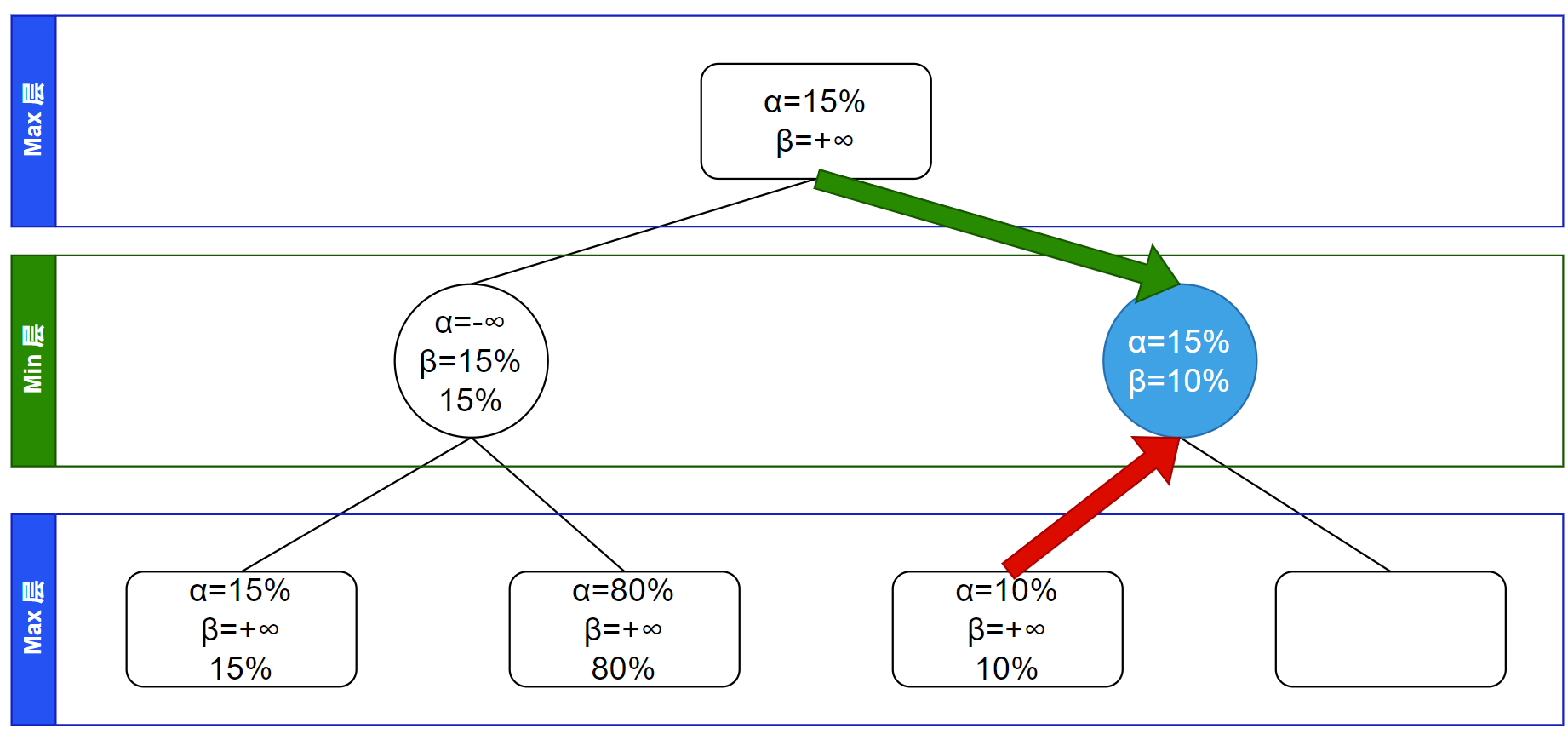
　　 继续递归，访问到其第一个子节点，这是叶子节点，不继承信息并自更新 $\alpha$、$\beta$ 信息（因为在 Max 层所以更新 $\alpha$ 信息）：

图
图 21：步骤 $9$

　　 回溯，在 Min 层所以更新 $\beta$ 信息为各子节点的所有 $\alpha$、$\beta$ 值的最小值：

图
图 22：步骤 $10$

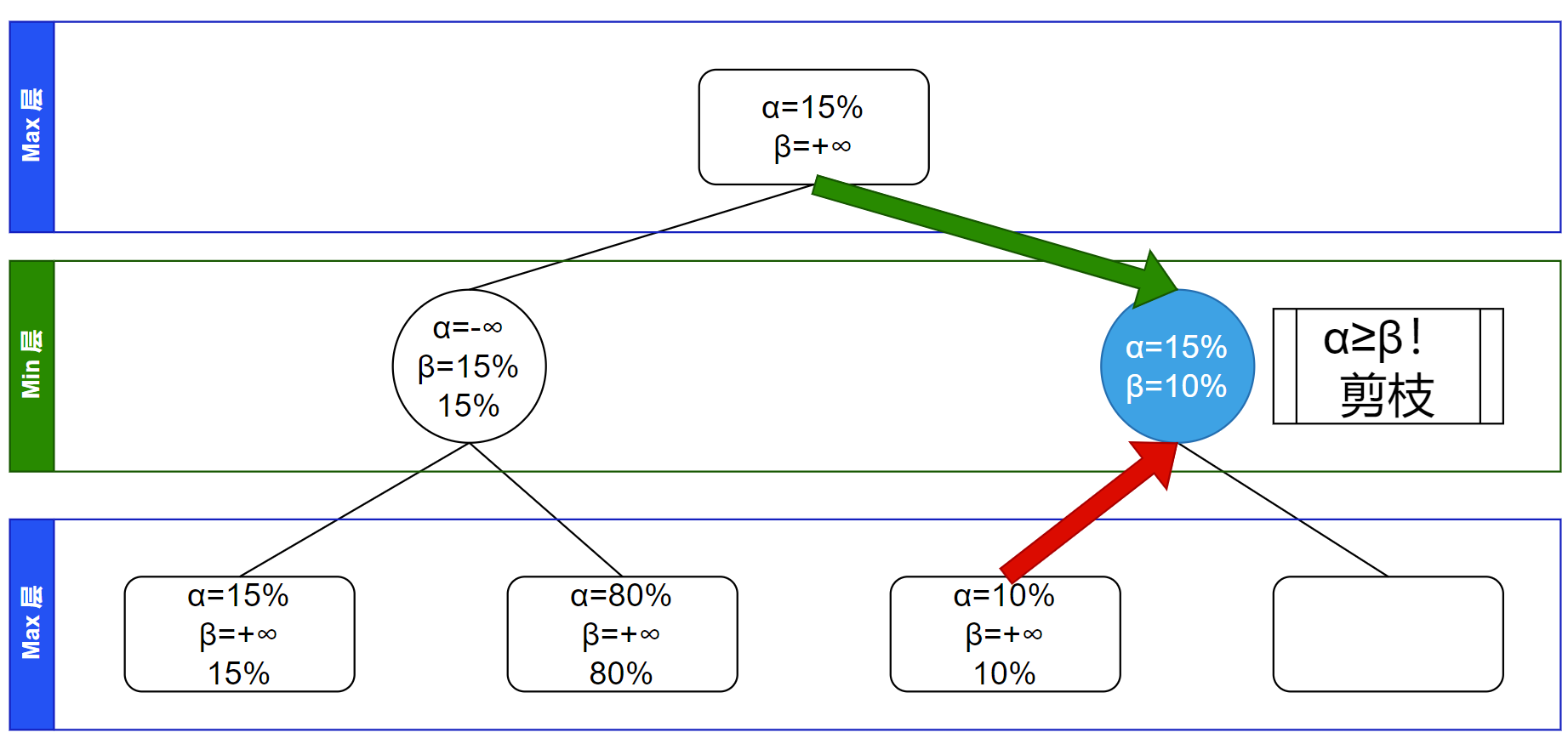
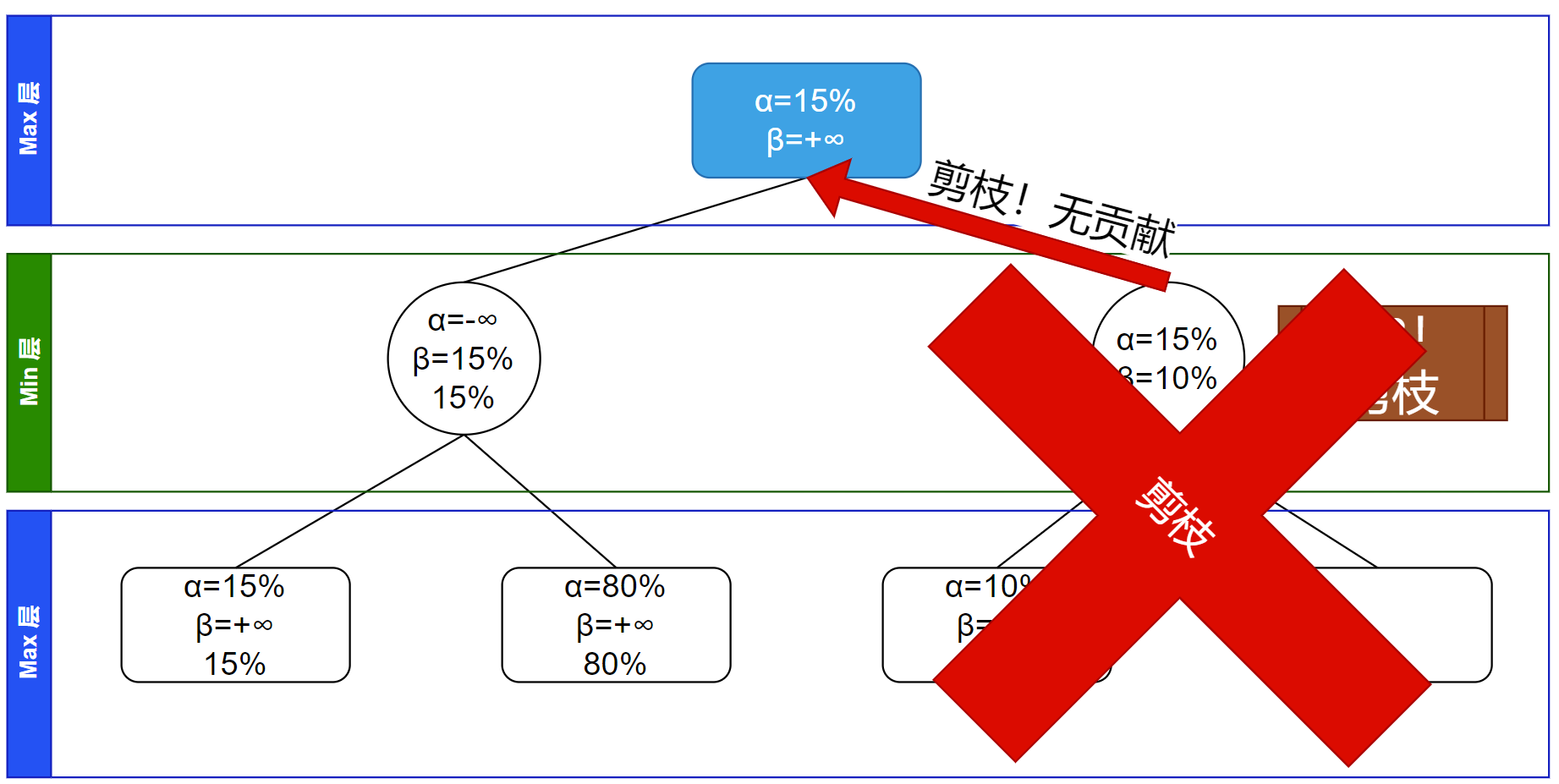
　　 此时发现这节点的 $\alpha \ge \beta$，这说明他不会对父节点贡献一个更优的信息了。剪枝，不再进行后面的搜索：

图
图 23：步骤 $11$

　　 $\alpha-\beta$ 剪枝对应于遍历这当前节点的所有子节点的循环被跳出（break 掉），所以不继续搜索这节点的子树：

图
图 24：步骤 $12$

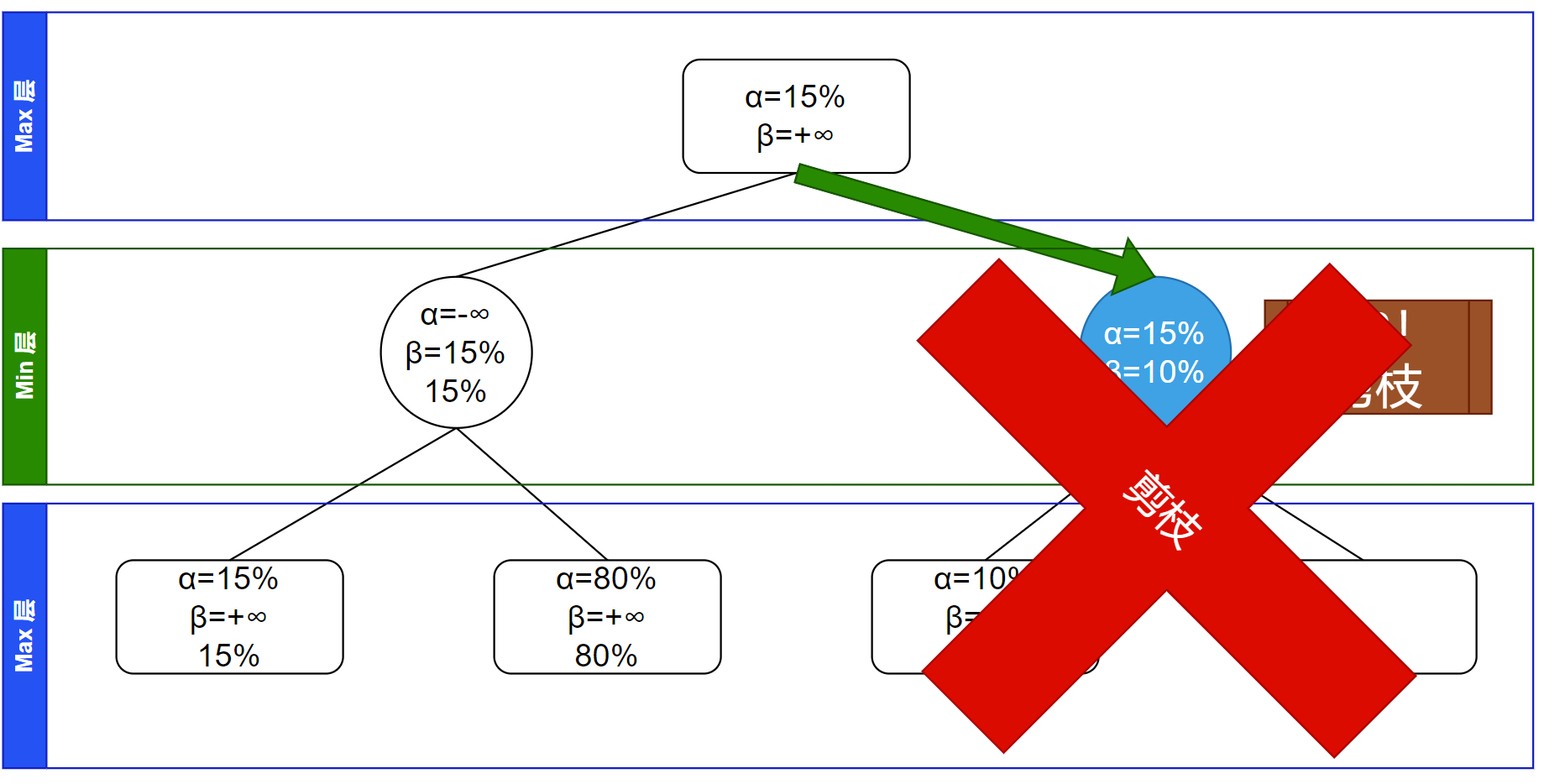
　　 回溯，因为剪枝了所以不传递信息，剪枝掉的节点的信息不会对其父节点产生贡献，所以可以不考虑传递信息的问题：

图
图 25：步骤 $13$

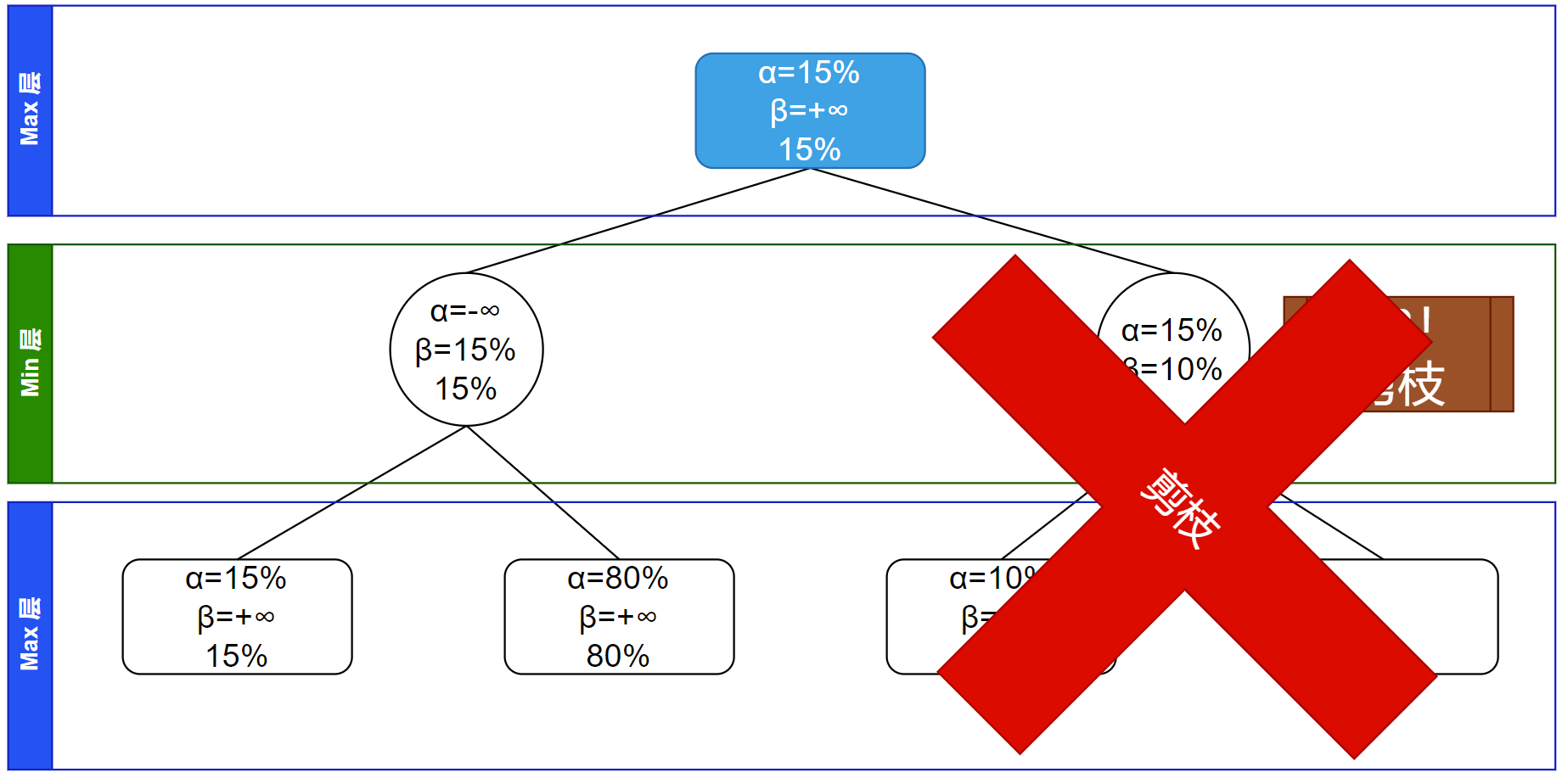
　　 发现没有其他可以搜索的内容，根节点的所有子节点都已经访问过，搜索结束，同时可以更新根节点的胜率信息，得到为全体子节点的最大值（因为在 Max 层）$15\%$：

图
图 26：步骤 $14$

代码实现

int alphabeta(node, dep, alpha, beta, isMax) {      
    if(dep == 0 || isLeafNode(node))// 是叶子节点
        return Evaluate();// 计算当前棋盘局面的胜率
    if(isMax) { // 在 Max 层
        for(auto child: childs[node]) {// 遍历子节点
            alpha = max(alpha,// alpha 更新为所有子节点的各α、β之最大值
			            alphabeta(child, dep-1, alpha, beta, not(isMax)))   
            if(alpha >= beta)  break;// 剪枝
        }
        return alpha
    }
    else {
        for(auto child: childs[node]) {
        	beta= min(beta,// beta 更新为所有子节点的各α、β之最小值
			          alphabeta(child, dep-1, alpha, beta, not(isMax))) 
            if(alpha >= beta)  break;// 剪枝
		}
        return beta;
    }
}

// to call: 
alphabeta(root, dep, -infty, +infty, true)

                     

© 小时科技 保留一切权利