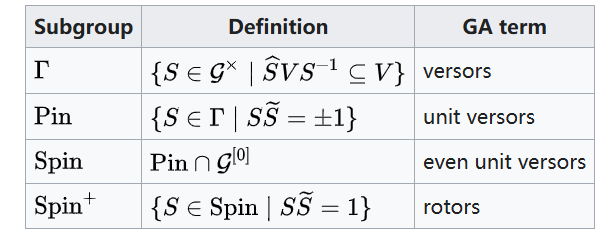几何代数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学中，几何代数（geometric algebra，亦称为 Clifford 代数）是一种能够表示和操作几何对象（如向量）的代数。几何代数建立在两个基本运算之上：加法与几何乘积。向量的乘法会生成更高维的对象，称为多向量。与其他用于处理几何对象的形式体系相比，几何代数的一个显著特征是它支持向量的除法（尽管通常不能对所有元素都定义），并且允许不同维度对象之间的加法。

　　 几何乘积最早由赫尔曼·格拉斯曼简要提出 \(^\text{[1]}\)，他当时主要致力于发展与之密切相关的外代数。1878 年，威廉·金顿·克利福德在格拉斯曼工作的基础上大幅扩展，形成了如今通常被称为 Clifford 代数的体系（尽管克利福德本人选择称其为 “几何代数”）。克利福德将 Clifford 代数及其乘法定义为格拉斯曼代数与哈密顿四元数代数的统一体。进一步引入格拉斯曼外积的对偶，可以得到 Grassmann–Cayley 代数。在 1990 年代末期，基于平面的几何代数以及共形几何代数（CGA）分别为欧几里得几何和经典几何提供了框架 \(^\text{[2]}\)。在实际应用中，这些运算及其若干衍生操作，使得代数中的元素、子空间与运算可以自然地对应到几何解释。然而，数十年来几何代数一度被忽视，其发展被当时新兴的向量分析（主要用于描述电磁学）所掩盖。直到 1960 年代，大卫·赫斯特尼斯再次推广 “几何代数” 这一术语，并强调它在相对论物理学中的重要性 \(^\text{[3]}\)。

　　 标量和向量在几何代数中具有其通常的解释，并且构成了代数中的不同子空间。双向量提供了一种比三维向量分析中的伪向量更自然的表示方式。伪向量通常通过叉乘得到，用来描述有向面积、有向旋转角、力矩、角动量以及磁场等物理量。三向量可以表示有向体积，依此类推。几何代数中的一种元素称为刀片，它可用于表示子空间以及到该子空间的正交投影。旋转与反射也能作为代数的元素来表示。与传统的向量代数不同，几何代数能够自然而然地适应任意维度以及任意二次型，例如相对论中的情况。

　　 在物理学中，几何代数的应用实例包括时空代数（以及较少使用的物理空间代数）。几何分析是几何代数的扩展，它结合了微分与积分，可以用来建立其他理论，例如复分析与微分几何——其方法是使用 Clifford 代数来取代传统的微分形式。

　　 几何代数的推广者中，最著名的是大卫·赫斯特尼斯 \(^\text{[4]}\) 和克里斯·多兰 \(^\text{[5]}\)，他们认为几何代数应当成为物理学的首选数学框架。支持者声称，它在许多领域中（包括经典力学、量子力学、电磁理论以及相对论）都能提供简洁而直观的描述 \(^\text{[6]}\)。此外，几何代数还在计算机图形学 \(^\text{[7]}\) 与机器人学中找到了计算工具的用途。

1. 定义与记号

　　 几何代数有多种不同的定义方式。赫斯特尼斯最初采用的是一种公理化方法，\(^\text{[8]}\) 这种方法 “充满几何意义”，并且与普遍的 Clifford 代数等价。\(^\text{[9]}\) 设 $V$ 是定义在一个域 $F$ 上的有限维向量空间，并带有一个对称双线性型（即内积，\(^\text{[b]}\) 例如欧几里得或洛伦兹度量）$g : V \times V \to F $,则二次空间 $(V, g)$ 的几何代数就是 Clifford 代数 $\operatorname{Cl}(V, g)$,其元素称为多向量。Clifford 代数通常被定义为张量代数的商代数。然而这种定义过于抽象，因此下列给出一种不依赖抽象代数的定义。

　　 定义

　　 一个带幺元的结合代数 $\operatorname{Cl}(V, g)$，若满足以下条件，则称为二次空间 $(V, g)$ 的 Clifford 代数 \(^\text{[10]}\)：

　　 为了涵盖退化对称双线性型的情况，最后一个条件必须加以修正。\(^\text{[c]}\) 可以证明，这些条件唯一地刻画了几何积。

　　 在本文的其余部分中，仅考虑实数情形，即 $F = \mathbb{R}$.记号 $\mathcal{G}(p,q)$（分别为 $ \mathcal{G}(p,q,r)$）将用来表示其双线性型 $g$ 的符号(signature)为 $(p,q)$（分别为 $(p,q,r)$）的几何代数。

　　 代数中的乘法称为几何积，而其所包含的外代数中的乘法称为外积（exterior product，常被称为楔积或外积 \(^\text{[d]}\)）。按照惯例，这两者的记号分别是：几何积：并列书写（即省略任何显式的乘号）；外积：使用符号 $\wedge$。

　　 上面给出的几何代数的定义仍然有些抽象，因此我们在这里总结一下几何积的性质。对于任意多向量 $A, B, C \in \mathcal{G}(p,q)$,有：

　　 至于外积，它也具有相同的性质，但最后一条被替换为：$a \wedge a = 0, \quad a \in V$

　　 请注意，在上述最后一个性质中，如果 $g$ 不是正定的，那么实数 $g(a,a)$ 不必是非负的。几何积的一个重要性质是存在可逆元素。对于一个向量 $a$，如果 $a^{2} \neq 0$,那么其逆元 $a^{-1}$ 存在，并且 $a^{-1} = g(a,a)^{-1} a$。然而，代数中的一个非零元素并不一定都有乘法逆元。例如，如果 $u \in V$ 且 $u^{2} = 1$,那么元素 $\frac{1}{2}(1+u)$ 既是一个非平凡的幂等元，又是一个非零的零因子，因此没有逆元 \(^\text{[e]}\)）。

　　 通常，我们会把 $\mathbb{R}$ 与 $V$ 分别与它们在自然嵌入 $\mathbb{R} \to \mathcal{G}(p,q), \quad V \to \mathcal{G}(p,q)$ 下的像识别起来。在本文中，这种识别被默认采用。自始至终，“标量” 与 “向量” 这两个术语，分别指的是 $\mathbb{R}$ 与 $V$ 的元素（以及它们在该嵌入下的像）。

几何积

图
图 1：给定两个向量 $a$ 和 $b$，若它们的几何积 $ab$ 是反对易的，则说明它们是垂直的（上图），因为 $a \cdot b = 0$；若它们的几何积是对易的，则说明它们是平行的（下图），因为 $a \wedge b = 0$。

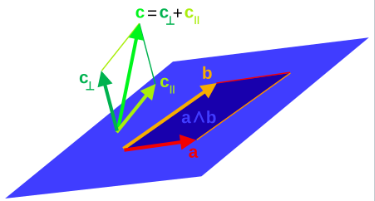
　　 对于向量 $a$ 和 $b$，任意两个向量的几何积可以写成对称部分与反对称部分的和： $$ ab = \tfrac{1}{2}(ab + ba) + \tfrac{1}{2}(ab - ba).~ $$ 因此，我们可以将向量的内积定义为： $$ a \cdot b := g(a, b),~ $$ 这样，对称部分就可以写为： $$ \tfrac{1}{2}(ab + ba) = \tfrac{1}{2}\left((a+b)^{2} - a^{2} - b^{2}\right) = a \cdot b.~ $$ 反过来说，双线性型 $g$ 完全由代数结构决定。反对称部分则是两个向量的外积，即包含在其中的外代数的乘积： $$ a \wedge b := \tfrac{1}{2}(ab - ba) = -(b \wedge a).~ $$ 于是，通过简单相加：$ab = a \cdot b + a \wedge b$ 这就是几何积的非广义（即向量形式）的表达式。

图
图 2：实外代数中次数为 $n$ 的元素的几何解释：当 $n=0$ 时，表示一个带符号的点；当 $n=1$ 时，表示一个有向线段（即向量）；当 $n=2$ 时，表示一个有向平面元；当 $n=3$ 时，表示一个有向体积。$n$ 个向量的外积可以形象化为任意一个 $n$ 维形状（例如 $n$-平行多胞体、$n$-椭球体）；其大小对应于超体积，而其取向由其 $(n-1)$ 维边界的方向，以及内部位于哪一侧所决定 \(^\text{[14][15]}\)。

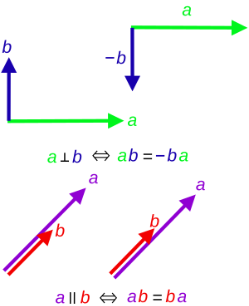
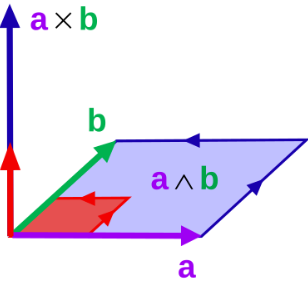
　　 内积与外积与标准向量代数中的一些熟悉概念相关。几何上，当两个向量 $a$ 和 $b$ 的几何积等于它们的内积时，它们是平行的；而当几何积等于它们的外积时，它们是垂直的。在一个几何代数中，如果任意非零向量的平方均为正数，那么两个向量的内积就可以看作是标准向量代数中的点积；而两个向量的外积则可以理解为由它们构成的平行四边形的带符号面积。在三维空间中，若二次型是正定的，则两个向量的叉积与它们的外积密切相关。

　　 大多数有研究价值的几何代数都具有非退化二次型。如果二次型完全退化，那么任意两个向量的内积恒为零，此时几何代数就会简化为一个外代数。除非特别说明，本文只讨论非退化几何代数。

　　 外积可以自然地扩展为代数中任意两个元素之间的结合的双线性二元运算，并满足以下恒等式： $$ 1 \wedge a_i = a_i \wedge 1 = a_i~ $$ $$ a_1 \wedge a_2 \wedge \cdots \wedge a_r = \frac{1}{r!}\sum_{\sigma \in S_r}\operatorname{sgn}(\sigma)\, a_{\sigma(1)}a_{\sigma(2)}\cdots a_{\sigma(r)},~ $$ 其中，求和是对所有指标的排列进行的，$\operatorname{sgn}(\sigma)$ 表示排列 $\sigma$ 的符号，$a_i$ 是向量（而不是代数中的一般元素）。 由于代数中的每个元素都可以表示为这种形式的乘积之和，这就为代数中任意两个元素定义了外积。由定义可知，外积构成一个交替代数。

　　 Clifford 代数的等价结构方程为 \(^\text{[16][17]}\)： $$ a_1 a_2 a_3 \dots a_n =\sum_{i=0}^{\lfloor \frac{n}{2} \rfloor}\; \sum_{\mu \in \mathcal{C}} (-1)^k \, \operatorname{Pf}\!\bigl(a_{\mu_1}\cdot a_{\mu_2},\dots,a_{\mu_{2i-1}}\cdot a_{\mu_{2i}}\bigr)\; a_{\mu_{2i+1}} \wedge \dots \wedge a_{\mu_n},~ $$ 其中，$\operatorname{Pf}(A)$ 是矩阵 $A$ 的 Pfaffian（帕夫算子）； $\mathcal{C}={\binom{n}{2i}}$ 表示将 $n$ 个指标划分为 $2i$ 个和 $n-2i$ 个部分的所有组合； $k$ 表示该组合的奇偶性。

　　 Pfaffian 为外代数提供了一种度量。正如 Claude Chevalley 指出的那样，当二次型为零时，Clifford 代数会退化为外代数。\(^\text{[18]}\) 从几何角度看，可以通过单形来发展 Clifford 代数，这样就能理解 Pfaffian 所起的作用。\(^\text{[19]}\) 这种推导方式也使 Pascal 三角形与单形之间建立了更好的联系，因为它为 Pascal 三角形第一列的 “1” 提供了一个解释。

刀、阶与基

　　 一个由 $r$ 个线性无关向量的外积构成的多向量称为刀，并称它的阶为 $r$\(^\text{[f]}\)。一个由若干个同阶 $r$ 的刀相加得到的多向量称为（同质的）$r$ 阶多向量。根据几何代数的公理及其封闭性，每一个几何代数中的多向量都可以表示为若干刀的和。

　　 设有一组 $r$ 个线性无关向量 $\{a_{1}, \ldots, a_{r}\}$，它们张成向量空间的一个 $r$ 维子空间。由此可以定义一个实对称矩阵（类似于 Gram 矩阵）： $$ [\mathbf{A}]_{ij} = a_i \cdot a_j~ $$ 根据谱定理，矩阵 $\mathbf{A}$ 可以通过一个正交矩阵 $\mathbf{O}$ 对角化为对角矩阵 $\mathbf{D}$： $$ \sum_{k,l} [\mathbf{O}]_{ik}\,[\mathbf{A}]_{kl}\,[\mathbf{O}^{\mathrm{T}}]_{lj} = \sum_{k,l} [\mathbf{O}]_{ik}\,[\mathbf{O}]_{jl}\,[\mathbf{A}]_{kl} = [\mathbf{D}]_{ij}~ $$ 由此定义一组新的向量 $\{e_{1}, \ldots, e_{r}\}$，称为正交基向量，它们由正交矩阵变换得到： $$ e_i = \sum_{j} [\mathbf{O}]_{ij}\, a_j~ $$ 由于正交变换保持内积，因此有 $e_i \cdot e_j = [\mathbf{D}]_{ij}$ 于是 $\{e_1, \ldots, e_r\}$ 互相正交。换句话说，两个不同的向量 $e_i \neq e_j$ 的几何积完全由它们的外积决定，更一般地： $$ \begin{aligned} e_1 e_2 \cdots e_r &= e_1 \wedge e_2 \wedge \cdots \wedge e_r \\ &=\left(\sum_{j} [\mathbf{O}]_{1j} a_j\right) \wedge \left(\sum_{j} [\mathbf{O}]_{2j} a_j\right) \wedge \cdots \wedge \left(\sum_{j} [\mathbf{O}]_{rj} a_j\right) \\ &= (\det \mathbf{O}) \, a_1 \wedge a_2 \wedge \cdots \wedge a_r \end{aligned}~ $$ 因此，每一个 $r$ 阶刀都可以写成 $r$ 个向量的外积。更一般地，如果允许退化几何代数，那么正交矩阵被一个分块矩阵所取代，其中非退化部分仍是正交的，而对角矩阵在退化维度上含有零值。若将非退化子空间中的新向量按如下方式归一化： $$ \widehat{e_i} = \frac{1}{\sqrt{|e_i \cdot e_i|}} \, e_i,~ $$ 那么这些归一化后的向量必须平方为 $+1$ 或 $-1$。根据 Sylvester 惯性定理，对角矩阵中平方为 $+1$ 的向量总数，以及平方为 $-1$ 的向量总数都是不变量。由此推广，记平方为 $+1$ 的基向量数为 $p$，平方为 $-1$ 的基向量数为 $q$，它们都是不变量。（若考虑退化情况，平方为零的基向量数也同样是不变量，并且可能非零。）我们将这种代数记作 $\mathcal{G}(p,q)$。例如：$\mathcal{G}(3,0)$ 对应三维欧几里得空间，$\mathcal{G}(1,3)$ 对应相对论时空，$\mathcal{G}(4,1)$ 对应三维空间的共形几何代数。

　　 所有可能的由 $n$ 个正交基向量按递增顺序相乘所形成的积（包括作为空积的 $1$），构成了整个几何代数的一个基（类似于 PBW 定理的情形）。例如，几何代数 $\mathcal{G}(3,0)$ 的一个基为： $$ \{1, e_{1}, e_{2}, e_{3}, e_{1}e_{2}, e_{2}e_{3}, e_{3}e_{1}, e_{1}e_{2}e_{3}\}~ $$ 以这种方式形成的基称为几何代数的标准基。对于向量空间 $V$ 的任一组正交基，都将生成另一组标准基。每一个标准基包含 $2^n$ 个元素。几何代数中的任意多向量都可以表示为标准基元素的线性组合。若标准基元素记作 $\{B_i \mid i \in S\}$，其中 $S$ 是一个指标集合，则任意两个多向量的几何积为： $$ \left(\sum_{i} \alpha_i B_i\right)\left(\sum_{j} \beta_j B_j\right) = \sum_{i,j} \alpha_i \beta_j B_i B_j .~ $$ 术语 “$k$-向量” 常用来描述只包含单一阶次元素的多向量。在高维空间中，有些这样的多向量并不是刀（即不能分解为 $k$ 个向量的外积）。例如，在 $\mathcal{G}(4,0)$ 中：$e_1 \wedge e_2 + e_3 \wedge e_4$ 就不能被分解。通常，这类代数元素没有直接的几何对象解释，但它们可能表示某些几何量，例如旋转。只有 $0$-、$1$-、$(n-1)$- 和 $n$-向量在 $n$ 维空间中总是刀。

向量子

　　 一个 $k$-versor 是可以表示为 $k$ 个可逆向量的几何积的多向量。\(^\text{[g][21]}\) 四元数中的单位四元数（最初由哈密顿称为 versors）可以与三维空间中的转子对应，就像二维实转子包含了复数一样；具体细节可参见 Dorst\(^\text{[22]}\)。

　　 一些作者使用 “versor 积” 一词来指代经常出现的一种情况：即一个操作数被 “夹在” 两个算子之间。旋转和反射（包括它们的外射 outermorphism）的描述就是这种 “夹心” 形式的例子。这些外射具有特别简单的代数形式。\(^\text{[h]}\) 具体来说，形如

　　 $V \to V : a \mapsto RaR^{-1}$ 的向量映射可以扩展为外射：$\mathcal{G}(V) \to \mathcal{G}(V) : A \mapsto RAR^{-1}$.

　　 由于算子和操作数都是 versor，因此还可能存在其他形式的例子，例如旋转一个转子、或者反射一个旋量——只要能为这些运算赋予某种几何或物理意义即可。

　　 根据 Cartan–Dieudonné 定理，每一个等距变换都可以表示为对超平面的反射。而既然复合的反射能产生旋转，那么正交变换就是 versor。

　　 在群论意义上，对于一个实的、非退化的几何代数 $\mathcal{G}(p,q)$，若将群 $\mathcal{G}^{\times}$ 识别为几何代数中所有可逆元素的群，Lundholm 给出了一个证明，说明 “versor 群”$\{v_{1} v_{2}\cdots v_{k} \in \mathcal{G} \mid v_{i} \in V^{\times}\}$（即所有可逆 versor 的集合）等同于 Lipschitz 群 $\Gamma$（又称 Clifford 群，不过 Lundholm 并不提倡这种叫法）\(^\text{[23]}\)。

Lipschitz 群的子群

　　 我们将次数对合记作 $\widehat{S}$，转置记作 $\widetilde{S}$。

　　 虽然 Lipschitz 群（定义为 $\{S \in \mathcal{G}^{\times} \mid \widehat{S} V S^{-1} \subseteq V\}$）和 versor 群（定义为 $\Bigl\{\prod_{i=0}^{k} v_i \ \Bigm| \ v_i \in V^{\times}, \ k \in \mathbb{N}\Bigr\}$）有不同的定义，但它们实际上是同一个群。Lundholm 将 Pin 群 $\operatorname{Pin}$、Spin 群 $\operatorname{Spin}$、以及正旋子群 $\operatorname{Spin}^{+}$ 定义为 Lipschitz 群的子群。\(^\text{[24]}\)

图
图 3

　　 多种关于旋量的分析都使用几何代数（GA）作为表示方法。\(^\text{[25]}\)

分级投影

　　 可以通过几何积自然诱导出的外积，在几何代数上建立一个 $\mathbb{Z}$-分级向量空间结构。

　　 由于在正交向量上几何积与外积相等，因此可以方便地利用一个正交基 $\{e_{1}, \ldots , e_{n}\}$ 来构造这种分级。

　　 几何代数中是 1 的数量倍的元素为 0 次（grade 0），称为标量。在 $\{e_{1}, \ldots , e_{n}\}$ 张成空间中的元素为 1 次（grade 1），即通常的向量。在 $\{e_{i}e_{j}\mid 1\leq i< j\leq n\}$ 张成空间中的元素为 2 次（grade 2），称为双向量。这一术语可以继续推广，直到最高次的 $n$-向量。另一种叫法是：$n$-向量称为伪标量；$(n-1)$-向量称为伪向量；以此类推。代数中的许多元素并不属于这种分级体系，因为它们是不同次数元素的和，这类元素称为混合次数。多向量的分级与最初选取的基无关。

　　 需要注意的是，这是一种向量空间的分级，但不是代数的分级。因为一个 $r$-刃（$r$-blade）与一个 $s$-刃的乘积，包含在从 0 次到 $(r+s)$-次刃的张成空间中，所以几何代数实际上是一个滤代数。

　　 一个多向量 $A$ 可以通过分级投影算子 $\langle A\rangle_r$ 来分解，该算子输出 $A$ 的 $r$ 次部分。因此： $$ A = \sum_{r=0}^{n} \langle A \rangle_{r}~ $$ 例如，两个向量的几何积：$ab = a \cdot b + a \wedge b = \langle ab \rangle_{0} + \langle ab \rangle_{2}$ 因为 $\langle ab \rangle_{0} = a \cdot b$，$\langle ab \rangle_{2} = a \wedge b$，而对除 $0$ 与 $2$ 之外的 $i$，都有 $\langle ab \rangle_{i} = 0$。

　　 一个多向量 $A$ 也可以分解为偶次部分与奇次部分，分别是所有偶次数分量与所有奇次数分量的和： $$ A^{[0]} = \langle A \rangle_{0} + \langle A \rangle_{2} + \langle A \rangle_{4} + \cdots~ $$ $$ A^{[1]} = \langle A \rangle_{1} + \langle A \rangle_{3} + \langle A \rangle_{5} + \cdots~ $$ 这可以看作是把原本的 $\mathbf{Z}$-分级向量空间退化为 $\mathbf{Z}_2$-分级向量空间的结果。几何积遵守这种更粗的分级，因此几何代数不仅是一个 $\mathbf{Z}_2$-分级向量空间，还是一个 $\mathbf{Z}_2$-分级代数（又称超代数，superalgebra）。

　　 若限制在偶次部分，两个偶元素的乘积仍然是偶的。这意味着偶多向量形成一个偶子代数。一个 $n$ 维几何代数的偶子代数，与一个 $(n-1)$ 维的完整几何代数代数同构（但不保留滤过结构或分级结构）。例如：$\mathcal{G}^{[0]}(2,0) \cong \mathcal{G}(0,1)$ 和 $\mathcal{G}^{[0]}(1,3) \cong \mathcal{G}(3,0)$

空间的表示

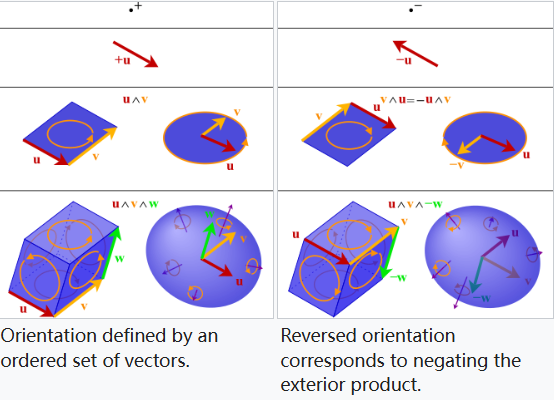
　　 几何代数用刀刃来表示向量空间 $V$ 的子空间，因此它们与来自 $V$ 的向量共存于同一个代数中。一个 $k$ 维子空间 $W \subseteq V$，可以通过选取一个正交基 $\{b_{1}, b_{2}, \ldots, b_{k}\}$，并使用几何积构造出刀刃 $ D = b_{1} b_{2} \cdots b_{k}$.存在多个刀刃可以表示同一个子空间 $W$；凡是表示 $W$ 的刀刃，都是 $D$ 的标量倍。它们可以分成两类：$D$ 的正倍数与负倍数。正倍数被称为与 $D$ 具有相同的定向，而负倍数则具有相反的定向。

　　 刀刃之所以重要，是因为几何操作（如投影、旋转和反射）依赖于外积下的可分解性，而这种可分解性由受限类别的 $n$-刀刃所提供，而当 $n \geq 4$ 时，一般的 $n$-级多向量并不具备这种性质。

单位拟标量

　　 在几何代数（GA）中，单位拟标量是一类重要的刀刃。对于向量空间 $V$ 的一个非退化子空间 $W$，其单位拟标量是由 $W$ 的一个正交归一基的向量相乘得到的刀刃。可以证明，如果 $I$ 和 $I'$ 都是 $W$ 的单位拟标量，则有 $I =\pm I', \quad I^{2} = \pm 1$.如果不选择正交归一基来表示 $W$，那么通过 Plücker 嵌入得到的是外代数中的一个向量，但仅能确定到一个比例因子。在几何代数与外代数之间的向量空间同构下，这对应于所有 $\alpha I$（其中 $\alpha \neq 0$）的等价类。正交归一化能够消除这种比例因子的歧义，但仍然会保留正负号的不确定性。

　　 设想构造几何代数 $\mathcal{G}(n,0)$，即在 $\mathbb{R}^n$ 上配备熟知的正定内积。若给定 $\mathbb{R}^n$ 中的一个平面（二维子空间），可以找到一个张成该平面的正交归一基 $\{b_{1}, b_{2}\}$，于是得到表示该平面的单位拟标量 $I = b_{1} b_{2}$.在由 $b_{1}, b_{2}$ 张成的平面内，任意两个向量的几何积都属于集合 $\{\alpha_{0}+\alpha_{1} I \mid\alpha_{i} \in \mathbb{R}\}$,也就是说，它必定是一个标量（0-向量）与一个双向量（2-向量）的和。

　　 根据几何积的性质，有 $I^{2} = b_{1} b_{2} b_{1} b_{2} = - b_{1} b_{2} b_{2} b_{1} = -1$.这种与虚数单位的相似性并非偶然：子空间 $\{\alpha_{0} + \alpha_{1} I \mid \alpha_{i} \in \mathbb{R}\}$ 作为 $\mathbb{R}$-代数同构于复数。因此，对于每一个二次型是正定的二维子空间，几何代数中都嵌入了一份复数的拷贝。

　　 有时在物理方程中可以辨认出虚数单位的存在。这类单位源自实代数中许多平方等于 $-1$ 的量，而这些量由于代数性质及其子空间间的相互作用而具有几何意义。

　　 在几何代数 $\mathcal{G}(3,0)$ 中，进一步出现了一个熟悉的情形。给定一个由正交归一向量 $e_{i}$ 组成的标准基，则所有二向量的集合由 $$ \{e_{3}e_{2}, \; e_{1}e_{3}, \; e_{2}e_{1}\}~ $$ 张成。若将它们分别标记为 $i$、$j$、$k$（暂时偏离我们使用大写字母的约定），那么由零向量与二向量张成的子空间正好是 $\{\alpha_{0} + i\alpha_{1} + j \alpha_{2} + k \alpha_{3} \mid \alpha_{i} \in \mathbb{R}\}$.这一集合正是 $\mathcal{G}(3,0)$ 的偶子代数，并且作为 $\mathbb{R}$-代数同构于四元数，另一种重要的代数系统。

内积与外积的扩展

　　 在几何代数中，将外积从向量扩展到整个代数是常见做法。这可以通过前面提到的 分级投影算子来实现： $$ C \wedge D := \sum_{r,s} \langle \langle C \rangle_{r} \langle D \rangle_{s} \rangle_{r+s}\text{（外积）}~ $$ 这种推广与前面基于反对称化的定义是一致的。另一个与外积相关的推广是换位子积：$C \times D := \tfrac{1}{2}(CD - DC)$（换位子积）\(^\text{[i]}\) 回归是外积的对偶（在此语境下，分别对应于 “交” 和 “并”）。元素的对偶表示允许在刀片 $C$ 和 $D$ 的情况下，定义它们的交（或 “meet”），其中对偶是相对于包含 $C$ 与 $D$ 的某个刀片来取的（最小的此类刀片就是 “join”）\(^\text{[27]}\)： $$ C \vee D := \big( (C I^{-1}) \wedge (D I^{-1}) \big) I~ $$ 其中 $I$ 是该代数的单位拟标量。与外积类似，回归积也是结合的。\(^\text{[28]}\)

　　 向量上的内积也可以推广，但有不止一种且互不等价的方式。Dorst (2002) 的论文对几何代数中发展出的几种不同的内积及其相互关系做了全面的论述，本文中的符号也取自该论文。许多作者在他们选择的推广中仍然使用与向量内积相同的符号（例如 Hestenes 和 Perwass）。目前尚未形成一致的记号体系。

　　 在这些向量内积的不同推广中，有： $$ C \;\rfloor\; D := \sum_{r,s} \langle \langle C \rangle_r \langle D \rangle_s \rangle_{s-r}\text{（左收缩）}~ $$ $$ C \;\lfloor\; D := \sum_{r,s} \langle \langle C \rangle_r \langle D \rangle_s \rangle_{r-s}\text{（右收缩）}~ $$ $$ C * D := \sum_{r,s} \langle \langle C \rangle_r \langle D \rangle_s \rangle_{0}\text{（标量积）}~ $$ $$ C \bullet D := \sum_{r,s} \langle \langle C \rangle_r \langle D \rangle_s \rangle_{|s-r|}\text{（“粗点积”或“胖点积”）}~ $$ Dorst（2002）提出了一个观点：与其使用 Hestenes 的内积，不如使用收缩，因为它们在代数上更规则，并且具有更清晰的几何解释。许多涉及收缩的恒等式在不对输入做任何限制的情况下都成立。例如： $$ C \;\rfloor\; D = (C \wedge (D I^{-1})) I~ $$ $$ C \;\lfloor\; D = I \big( (I^{-1} C) \wedge D \big)~ $$ $$ (A \wedge B) * C = A * (B \;\rfloor\; C)~ $$ $$ C * (B \wedge A) = (C \;\lfloor\; B) * A~ $$ $$ A \;\rfloor\; (B \;\rfloor\; C) = (A \wedge B) \;\rfloor\; C~ $$ $$ (A \;\rfloor\; B) \;\lfloor\; C = A \;\rfloor\; (B \;\lfloor\; C)~ $$ 使用左收缩作为向量内积的推广有若干优点，例如：恒等式 $ab = a \cdot b+ a \wedge b$ 能够自然推广为 $aB = a \;\rfloor\; B + a \wedge B$ 其中 $a$ 是任意向量，$B$ 是任意多向量。此外，投影运算 $\mathcal{P}_{b}(a) = (a \cdot b^{-1}) b$ 也能被推广为 $\mathcal{P}_{B}(A) = (A \;\rfloor\; B^{-1}) \;\rfloor\; B$ 其中 $B$ 是任意刀，$A$ 是任意多向量（在 $B$ 退化为零刀的情况下需作轻微修改，见下文）。

对偶基

　　 设 $\{e_{1},\ldots ,e_{n}\}$ 是向量空间 $V$ 的一组基，即 $n$ 个线性无关的向量，张成了 $n$ 维向量空间 $V$。与 $\{e_{1},\ldots ,e_{n}\}$ 对偶的基是对偶空间 $V^{*}$ 中的一组元素，它与这组基构成一个双正交系统，记作 $\{e^{1},\ldots ,e^{n}\}$，其满足条件 $$ e^{i}\cdot e_{j} = \delta^{i}{}_{j},~ $$ 其中 $\delta$ 是克罗内克 δ。

　　 如果在 $V$ 上给定一个非退化的二次型，则 $V^{*}$ 可以自然地与 $V$ 等同，此时对偶基可以被看作是 $V$ 中的元素，但它们一般并不与原始基向量相同。

　　 进一步地，若给定 $V$ 的几何代数（GA），则设 $$ I = e_{1} \wedge \cdots \wedge e_{n}~ $$ 是由基 $\{e_{1},\ldots ,e_{n}\}$ 构造的伪标量（pseudoscalar，注意它不一定平方为 $\pm 1$）。对偶基向量可以通过以下公式构造： $$ e^{i} = (-1)^{i-1} \big( e_{1} \wedge \cdots \wedge \check{e}_{i} \wedge \cdots \wedge e_{n} \big) I^{-1},~ $$ 其中 $\check{e}_{i}$ 表示在楔积中省略第 $i$ 个基向量。

　　 对偶基也称为倒易基或倒易标架。

　　 对偶基的一个主要用途是将向量分解为分量。给定一个向量 $a$，可以定义标量分量 $a^{i}$ 为 $$ a^{i} = a \cdot e^{i},~ $$ 于是向量 $a$ 可以分解为基向量的分量形式： $$ a = \sum_{i} a^{i} e_{i}.~ $$ 我们同样可以定义另一种标量分量 $a_{i}$ 为 $$ a_{i} = a \cdot e_{i},~ $$ 于是向量 $a$ 也可以用对偶基来分解为： $$ a = \sum_{i} a_{i} e^{i}.~ $$ 如上所定义的几何代数向量子空间的对偶基，可以推广到覆盖整个代数。\(^\text{[29]}\) 为了简洁，我们使用单个大写字母来表示一组有序的向量指标。即写作 $$ J = (j_{1}, \dots , j_{n}) \ ,~ $$ 其中 $j_{1} < j_{2} < \cdots < j_{n}$。于是一个基底刀片（basis blade）可写为 $$ e_{J} = e_{j_{1}} \wedge e_{j_{2}} \wedge \cdots \wedge e_{j_{n}} \ .~ $$ 与之对应的倒易刀片则将指标顺序反转： $$ e^{J} = e^{j_{n}} \wedge \cdots \wedge e^{j_{2}} \wedge e^{j_{1}} \ .~ $$ 类似于向量的情况，可以证明 $$ e^{J} * e_{K} = \delta^{J}_{K} \ ,~ $$ 其中 $*$ 表示标量积。

　　 给定一个多向量 $A$，我们可以定义标量分量为 \(^\text{[30]}\) $$ A^{ij\cdots k} = (e^{k} \wedge \cdots \wedge e^{j} \wedge e^{i}) * A \ ,~ $$ 据此，$A$ 可以分解为分量刀片： $$ A = \sum_{i< j<\cdots < k} A^{ij\cdots k} \, e_{i} \wedge e_{j} \wedge \cdots \wedge e_{k} \ .~ $$ 我们也可以换一种方式定义标量分量： $$ A_{ij\cdots k} = (e_{k} \wedge \cdots \wedge e_{j} \wedge e_{i}) * A \ ,~ $$ 据此，$A$ 可以分解为： $$ A = \sum_{i< j<\cdots < k} A_{ij\cdots k} \, e^{i} \wedge e^{j} \wedge \cdots \wedge e^{k} \ .~ $$

线性函数

　　 虽然旋量（versor）更容易使用，因为它可以直接在代数中表示为多向量，但旋量只是多向量上线性函数的一个子群，在必要时仍然可以使用。一个维数为 $n$ 的向量空间的几何代数由 $2^{n}$ 个基元素张成。若一个多向量用代数基底的系数构成的 $2^{n} \times 1$ 实列向量矩阵表示，那么该多向量的所有线性变换都可以表示为一个 $2^{n} \times 2^{n}$ 实矩阵的矩阵乘法。

　　 然而，这种一般的线性变换允许任意的不同阶次之间的交换，例如把一个标量 “旋转” 成一个向量，这在几何上没有明显的解释。

　　 更值得关注的是从向量到向量的一般线性变换。在自然限制为保持所诱导的外代数结构时，该线性变换的外延映射就是旋量的唯一扩展。\(^\text{[k]}\) 如果 $f$ 是一个将向量映射到向量的线性函数，那么它的外延映射就是满足如下规则的函数： $$ \underline{\mathsf{f}}(a_{1}\wedge a_{2}\wedge \cdots \wedge a_{r}) \;=\; f(a_{1}) \wedge f(a_{2}) \wedge \cdots \wedge f(a_{r})~ $$ 对于一个刀片成立，并且通过线性性推广到整个代数。

2. 几何的建模

　　 尽管很多注意力都集中在共形几何代数（CGA）上，但几何代数（GA）并不只是单一的一个代数，而是一个具有相同基本结构的代数家族。\(^\text{[31]}\)

向量空间模型

　　 $\mathcal{G}(2,0)$ 的偶子代数与复数同构。可以这样看：把一个向量 $P$ 按正交归一基展开，然后用基向量 $e_{1}$ 左乘，得到 $$ Z = e_{1}P = e_{1}(x e_{1} + y e_{2}) = x(1) + y(e_{1}e_{2}),~ $$ 其中我们将 $i \mapsto e_{1}e_{2}$，因为 $$ (e_{1}e_{2})^{2} = e_{1}e_{2}e_{1}e_{2} = -e_{1}e_{1}e_{2}e_{2} = -1.~ $$ 类似地，$\mathcal{G}(3,0)$ 的偶子代数，其基为 $\{1, \; e_{2}e_{3}, \; e_{3}e_{1}, \; e_{1}e_{2}\}$,与四元数同构，可以通过如下对应关系看出：$i \mapsto -e_{2}e_{3}, \quad j \mapsto -e_{3}e_{1}, \quad k \mapsto -e_{1}e_{2}$.

　　 每个结合代数都有矩阵表示；将三个笛卡尔基向量替换为泡利矩阵，就得到 $\mathcal{G}(3,0)$ 的一个表示：

　　 $$ e_{1} = \sigma_{1} = \sigma_{x} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad e_{2} = \sigma_{2} = \sigma_{y} = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}, \quad e_{3} = \sigma_{3} = \sigma_{z} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.~ $$ 点乘 “泡利向量”（一个二重矢）：

　　 $\sigma = \sigma_{1}e_{1} + \sigma_{2}e_{2} + \sigma_{3}e_{3} $ 与任意向量 $a$ 和 $b$ 相乘，得到：$(\sigma \cdot a)(\sigma \cdot b) = a \cdot b + a \wedge b$（等价地，从式子直接观察可得：$ a \cdot b + i \sigma \cdot (a \times b)$）。

时空模型

　　 在物理学中，几何代数的主要应用是闵可夫斯基 $3+1$ 时空的几何代数 $\mathcal{G}(1,3)$，称为时空代数 \(^\text{[3]}\)；或者较少使用的 $\mathcal{G}(3,0)$，被解释为物理空间代数。

　　 在 STA 中，时空中的点可以简单地用向量表示；而在 APS 中，$(3+1)$ 维时空中的点则用副向量表示，它由三维空间向量加上一维标量（时间）组成。

　　 在时空代数中，电磁场张量可以用双向量表示为：$F= (E+icB)\gamma_0$\(^\text{[32]}\) 其中：$i = \gamma_0\gamma_1\gamma_2\gamma_3$ 是单位伪标量（或四维体积元）；$\gamma_0$ 是时间方向上的单位向量；$E$ 和 $B$ 分别是经典的电场向量与磁场向量（它们的时间分量为零）。利用四维电流 $J$，麦克斯韦方程便可以改写为该代数框架下的形式。

图
图 4

　　 在几何微积分中，向量的并列书写（如 $DF$）表示的是几何乘积，它可以分解为以下两部分：$DF = D \;\rfloor\; F + D \wedge F$ 其中：$D$ 是任意时空中的**协向量导数，在平直时空中退化为常见的 $\nabla$；$\bigtriangledown$（▽）在闵可夫斯基 $4$-维时空中的作用类似于欧几里得 $3$-维空间中的 $\nabla$，并且它与达朗贝尔算子 $\Box$ 的关系是：$\Box = \bigtriangledown^2$ 事实上，对于由指向未来的类时向量 $\gamma_0$ 所表示的观察者，有： $$ \gamma_0 \cdot \bigtriangledown = \frac{1}{c} \frac{\partial}{\partial t}~ $$ $$ \gamma_0 \wedge \bigtriangledown = \nabla~ $$ 洛伦兹度量空间中的推动具有与欧几里得空间中旋转相同的数学表达式 $e^{\beta}$，其中：$\beta$ 是由时间方向与相关空间方向生成的双向量；在欧几里得情形下，$\beta$ 则由两个空间方向生成。这使得两者之间的 “类比” 几乎达到了完全对应的程度。

　　 狄拉克矩阵是 $\mathcal{G}(1,3)$ 的一种表示形式，这说明了它们与物理学家使用的矩阵表示是等价的。

齐次模型

　　 齐次模型通常指一种射影表示，其中向量空间的一维子空间的元素代表几何中的点。

　　 在一个 $n$ 维空间的几何代数中，旋量表示一组具有 $n(n-1)/2$ 个自由度的变换，这些自由度对应于旋转。例如：当 $n = 3$ 时，自由度为 3；当 $n = 4$ 时，自由度为 6。几何代数常用于建模射影空间，即作为齐次模型：点、直线、平面等用代数中一类等价元素表示，这些元素之间相差一个可逆的标量因子。

　　 在一个 $n+1$ 维空间中，旋量拥有 $n(n-1)/2 + n$ 个自由度，这与 $n$ 维空间中旋转和平移的自由度总数一致。

　　 这种情况出现在射影几何代数中，它被用于表示欧几里得几何中的欧几里得等距变换 \(^\text{[33][34][35]}\)，因此涵盖了工程领域中绝大多数的几何应用。在该模型中，通过向三维欧几里得空间添加一个退化维度，构造出代数 $\mathcal{G}(3,0,1)$ 通过对适当子空间的识别，可以用该代数中的元素分别表示点、直线和平面。在这个框架下，向量乘积可以表示所有正向的欧几里得等距变换（它们在三维空间中总是螺旋运动），以及所有非正向的欧几里得等距变换，包括反射、旋转反射、平移反射以及点反射。此外，PGA 还能从 $\mathcal{G}(3,0,1)$ 中推导出投影、交会和角度公式；通过对代数进行极小的扩展，还可以推导出距离与连接。

　　 PGA 是一个将几何代数与齐次几何表示结合起来的广泛应用的系统。除了 PGA 外，还有其他一些齐次模型。例如，下面将讨论的保形模型就是齐次的，“圆锥几何代数”\(^\text{[36]}\) 也是如此。此外，“基于平面的几何代数” 则提供了椭圆几何和双曲几何的齐次模型，并将它们与基于 PGA 推导出的欧几里得几何进行了比较。

保形模型

图
图 5

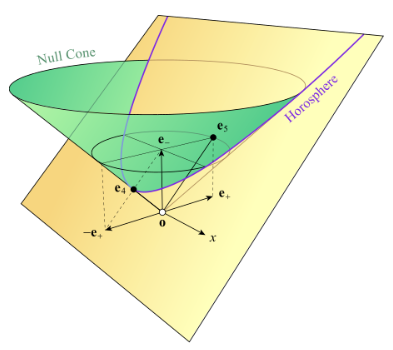
　　 在几何代数框架下，欧几里得空间 $\mathbb{E}^3$（连同一个无穷远保形点）通过将欧几里得点识别为 5 维 CGA 向量子空间的 4 维零锥中的一维子空间，被射影嵌入到保形几何代数 $\mathcal{G}(4,1)$ 中。这种表示允许将所有保形变换都表达为旋转或反射，并且保持协变性，还将射影几何中的关联关系扩展到了圆、球等曲面对象。

　　 具体来说，在生成 $\mathcal{G}(3,0)$ 的向量空间基底上，增加两个相互正交的基向量 $e_{+}$ 和 $e_{-}$，并定义它们满足：$e_{+}^2 = +1, \quad e_{-}^2 = -1$ 接着定义零向量：
原点对应的点：$n_{\text{o}} = \frac{1}{2}(e_{-} - e_{+})$
无穷远的保形点：$n_{\infty} = e_{-} + e_{+}$ 并且满足：
$n_{\infty} \cdot n_{\text{o}} = -1$

　　 （一些文献中会把 $e_4 = n_{\text{o}}$，$e_5 = n_{\infty}$\(^\text{[37]}\)。）这种构造与射影几何中齐次坐标的处理方式有一定相似之处。在该框架下，$\mathbb{R}^3$ 中的欧几里得变换可以建模为 $\mathbf{R}^{4,1}$ 某个子空间中的正交变换。

　　 CGA 是几何代数中一个快速发展、不断演化的研究领域，目前也在探索其在相对论物理中的应用潜力。

模型表

　　 请注意，在此列表中，参数 $p$ 和 $q$ 可以互换，名称依然适用；例如，仅需进行极少的调整即可（参见符号约定）。例如，$\mathcal{G}(3,1,0)$ 和 $\mathcal{G}(1,3,0)$ 都被称为时空代数 \(^\text{[38]}\)。

表1：
名称 符号 刀刃，例如代数可表示的定向几何对象 旋量，例如代数可表示的保持方向的变换 备注
双曲数 $\mathcal{G}(1,0,0)$ 点 此处 $p$ 和 $q$ 不能互换
复数 $\mathcal{G}(0,1,0)$ 点 此处 $p$ 和 $q$ 不能互换
对偶数 $\mathcal{G}(0,0,1)$ 点 此处 $p$ 和 $q$ 不能互换
向量空间几何代数 物理空间代数 $\mathcal{G}(3,0,0)$ 过原点的平面和直线 旋转，例如 $\mathrm{SO}(3)$ 最早由威廉·克利福德发现的几何代数
射影几何代数、刚体几何代数、基于平面的几何代数 $\mathcal{G}(3,0,1)$ 空间中任意位置的平面、直线和点 旋转和平移，例如刚体运动 $\mathrm{SE}(3)$，也称为 $\mathrm{SO}(3,0,1)$ 对符号进行轻微修改即可用于建模双曲空间和椭圆空间（详见主条目）。无法建模整个“射影”群。
时空代数 $\mathcal{G}(3,1,0)$ 时空中经过原点的体、平面和直线 旋转与时空推动，例如 $\mathrm{SO}(3,1)$（洛伦兹群） 是规范引力理论的基础。
射影化时空代数 $\mathcal{G}(3,1,1)$ 时空中的体、平面、直线和点（事件） 旋转、平移和时空推动（庞加莱群，Poincaré group）
保形几何代数 $\mathcal{G}(4,1,0)$ 空间中任意位置的球体、圆、点对（或偶极子）、圆点、平点、直线和平面 保持角度的空间变换（保形群 $\mathrm{SO}(4,1)$）
保形时空代数 $\mathcal{G}(4,2,0)$ 时空中的球体、圆、平面、直线、光锥、匀加速物体的轨迹 时空的保形变换，例如保持时空间隔弧长上快速度的变换 与扭量理论相关。
母代数 \(^\text{[41]}\) $\mathcal{G}(3,3,0)$ 未知 射影群
圆锥曲线几何代数 二次保形二维几何代数 \(^\text{[42][36]}\) $\mathcal{G}(5,3,0)$ 点、点对/点三元组/点四元组、圆锥曲线、最多由 6 个独立圆锥曲线组成的线束 反射、平移、旋转、缩放以及其他变换 圆锥曲线可以通过控制点以及圆锥曲线的线束构造出来。
二次保形几何代 \(^\text{[43]}\) $\mathcal{G}(9,6,0)$ 点、最多由 8 个点组成的点组、二次曲面、圆锥曲线、二次曲面上的圆锥曲线（如球面圆锥曲线）、最多由 9 个二次曲面组成的线束 反射、平移、旋转、缩放及其他变换 二次曲面可以通过控制点构造，并且可以确定其表面法线。
双重保形几何代数 \(^\text{[44]}\) $\mathcal{G}(8,2,0)$ 点、达布圆环面、二次曲面 反射、平移、旋转、缩放及其他变换 利用两个独立的 CGA 基底的双向量来表示具有 15 个唯一系数的 5×5 对称“矩阵”。但这种方法的代价是失去了通过点进行交点运算和构造的能力。

3. 向量空间模型中的几何解释

投影与拒斥

图
图 6：在三维空间中，双向量 $a \wedge b$ 定义了一个二维平面子空间（浅蓝色，沿指示方向无限延伸）。任意三维空间中的向量 $c$ 都可以分解为：在该平面上的投影 $c_{\parallel}$；从该平面上的拒斥 $c_{\perp}$。

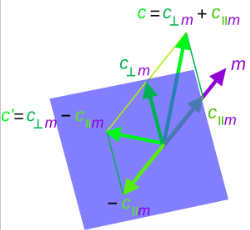
　　   对于任意向量 $a$ 和任意可逆向量 $m$： $$ a = a m m^{-1} = (a \cdot m + a \wedge m)m^{-1} = a_{\parallel m} + a_{\perp m},~ $$ 其中，向量 $a$ 在 $m$ 上的投影为： $$ a_{\parallel m} = (a \cdot m)m^{-1},~ $$ 而向量 $a$ 相对于 $m$ 的拒斥为： $$ a_{\perp m} = a - a_{\parallel m} = (a \wedge m)m^{-1}.~ $$ 利用 $k$-刃 $B$ 来表示向量空间 $V$ 的一个子空间，并且由于任意多向量最终都可以用向量表达，这一概念可以推广为： 将任意多向量 $A$ 投影到任意可逆 $k$-刃 $B$ 上： $$ \mathcal{P}_{B}(A) = (A \;\rfloor\; B) \;\rfloor\; B^{-1},~ $$ 而拒斥部分定义为： $$ \mathcal{P}_{B}^{\perp}(A) = A - \mathcal{P}_{B}(A).~ $$ 投影与拒斥可以推广到零刃 $B$，方法是将逆元 $B^{-1}$ 替换为相对于收缩乘积的伪逆 $B^{+}$\(^\text{[m]}\)。对于非零刃，这种推广后的投影结果与原始定义的结果是一致的 \(^\text{[45][46]}\)。对于零刃 $B$，应使用先进行第一次收缩，再作用于伪逆的投影定义 \(^\text{[n]}\)，只有这样，结果才能确保位于 $B$ 所表示的子空间内 \(^\text{[45]}\)。该投影通过线性性可以推广到任意多向量 $A$\(^\text{[o]}\)。然而，投影在 $B$ 上不是线性的，并且无法推广到不是刃的对象 $B$。

反射

　　 超平面中的简单反射可以通过与单个向量的共轭运算在几何代数中方便地表示。这些反射运算可用于生成一般旋转反射和旋转的群。

图
图 7：向量 $c$ 沿向量 $m$ 的反射。只有 $c$ 在 $m$ 方向上的分量会被取反。

　　 向量 $c$ 关于向量 $m$ 的反射（等价于在与 $m$ 正交的超平面上的反射），实际上就是将 $c$ 在 $m$ 方向上的分量取反。反射后的结果为： $$ c' = -c_{\parallel m} + c_{\perp m} = -(c \cdot m)m^{-1} + (c \wedge m)m^{-1} = (-m \cdot c - m \wedge c)m^{-1} = -m c m^{-1}.~ $$ 当空间维数 $n \geq 4$ 时，这并不是唯一可以视为 “反射” 的一般操作。一般反射可以表示为任意奇数次单轴反射的复合。因此，向量 $a$ 的一般反射 $a'$ 可写为： $$ a \;\mapsto\; a' = - M a M^{-1},~ $$ 其中： $$ M = p q \cdots r, \quad M^{-1} = (p q \cdots r)^{-1} = r^{-1} \cdots q^{-1} p^{-1}.~ $$ 如果定义沿着一个非零向量 $m$ 对向量乘积的反射为：该乘积中的每个向量都沿着同一个 $m$ 进行反射，那么：对于奇数个向量的乘积（例如 $a b c$）： $$ (abc)' = a'b'c' = (-mam^{-1})(-mbm^{-1})(-mcm^{-1}) = -ma(m^{-1}m)b(m^{-1}m)cm^{-1} = -mabc m^{-1}.~ $$ 对于偶数个向量的乘积（例如 $a b c d$）： $$ (abcd)' = a'b'c'd' = (-mam^{-1})(-mbm^{-1})(-mcm^{-1})(-mdm^{-1}) = m a b c d m^{-1}.~ $$ 由于任意多向量最终都可以用向量表示，任意多向量 $A$ 的一般反射（使用任意反射旋量 $M$）可以写为： $$ A \;\mapsto\; M \alpha(A) M^{-1},~ $$ 其中 $\alpha$ 是一种关于向量空间原点反射的自同构（$v \mapsto -v$），并且通过线性扩展作用于整个代数。

旋转

图
图 8：在一个平面内旋转向量的旋量，会使向量旋转角度 $\theta$。也就是说：$x \;\mapsto\; R_{\theta} \, x \, \widetilde{R}_{\theta}$ 表示向量 $x$ 绕该平面旋转角度 $\theta$。其中，向量 $u$ 和 $v$ 之间的夹角为：$\theta / 2.$ 类似的解释也适用于用一般多向量 $X$ 代替向量 $x$ 的情形。\(^\text{[13]}\)

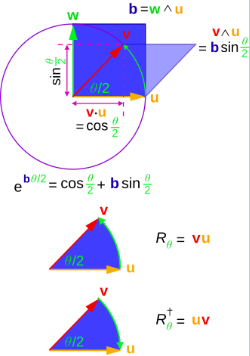
　　 如果我们有一个向量乘积 $R = a_1 a_2 \cdots a_r$，则它的逆序记作： $$ \widetilde{R} = a_r \cdots a_2 a_1.~ $$ 举例：假设 $R = a b$，那么： $$ R \widetilde{R} = a b b a = a b^2 a = a^2 b^2 = b a^2 b = b a a b = \widetilde{R} R.~ $$ 通过缩放 $R$ 使得：$R \widetilde{R} = 1$，则有： $$ (R v \widetilde{R})^2 = R v^2 \widetilde{R} = v^2 R \widetilde{R} = v^2,~ $$ 这意味着变换 $R v \widetilde{R}$ 保持向量 $v$ 的长度不变。此外，还可以证明： $$ (R v_1 \widetilde{R}) \cdot (R v_2 \widetilde{R}) = v_1 \cdot v_2,~ $$ 因此，变换 $R v \widetilde{R}$ 同时保持长度和角度，所以它可以被识别为一次旋转或旋转反射。如果 $R$ 可以表示为偶数个向量的乘积，则 $R$ 是一次纯旋转，称为旋量，它是几何代数中所谓向量乘子的一个实例。

　　 旋转向量的一般方法是构造如下形式的多向量：$R = e^{-B\theta / 2}$，其中： $\theta$ 表示旋转角度，$B$ 是定义旋转平面和方向的 2-刃。

　　 旋量是四元数在 $n$ 维空间中的推广。

4. 示例与应用

由向量张成的平行多胞体的超体积

　　 对于由向量 $a$ 和 $b$ 张成的平行四边形，有： $$ a \wedge b = \bigl((a \wedge b)b^{-1}\bigr)b = a_{\perp b} b~ $$ 由此可知，外积 $a \wedge b$ 在几何上等同于 “高” 与 “底” 的乘积，即平行四边形的面积。

　　 类似地，对于由任意多个向量 $a_1, a_2, \ldots, a_n$ 张成的 $n$ 维平行多胞体，它们的外积：$\bigwedge_{i=1}^n a_i$ 的模长等于该 $n$ 维平行多胞体的体积。需要注意的是，$n$-向量本身并不一定真的具有平行多胞体的几何形状——这只是一个方便的可视化方法。无论其几何形状如何，其体积的大小总是等于相应平行多胞体的体积。

直线与平面的交点

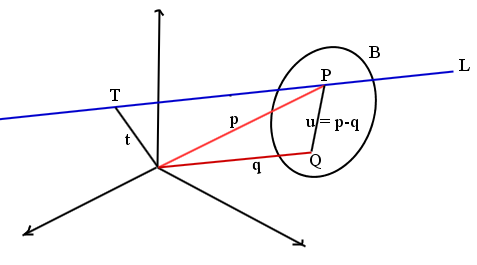
　　 我们可以用参数形式定义直线：$p = t + \alpha v$，其中：$p$ 和 $t$ 分别是点 $P$ 和点 $T$ 的位置向量，$v$ 是直线的方向向量。

图
图 9：一条由点 T 和 P（待求点）定义的直线 L，以及一条由包含点 P 和 Q 的双向量 B 定义的平面。

　　 于是有： $$ B \wedge (p - q) = 0~ $$ $$ B \wedge (t + \alpha v - q) = 0~ $$ 解得： $$ \alpha = \frac{B \wedge (q - t)}{B \wedge v},~ $$ 进而得到直线与平面的交点： $$ p = t + \left(\frac{B \wedge (q - t)}{B \wedge v}\right)v.~ $$

旋转系统

　　 在几何代数中，旋转量（如力矩或角动量）用双向量来表示。设在一个任意平面上存在一条圆轨迹，该平面由一组正交单位向量 $\widehat{u}$ 和 $\widehat{v}$ 定义，用角度 $\theta$ 来参数化该轨迹： $$ \mathbf{r} = r (\widehat{u} \cos\theta + \widehat{v} \sin\theta) = r \widehat{u} (\cos\theta + \widehat{u} \widehat{v} \sin\theta)~ $$ 将该平面的单位双向量定义为虚数单位： $$ i = \widehat{u} \widehat{v} = \widehat{u} \wedge \widehat{v},~ $$ 并且： $$ i^2 = -1,~ $$ 则该轨迹向量可以方便地写成复指数形式： $$ \mathbf{r} = r \widehat{u} e^{i\theta}.~ $$ 对角度 $\theta$ 求导： $$ \frac{d\mathbf{r}}{d\theta} = r \widehat{u} i e^{i\theta} = \mathbf{r} i.~ $$

图
图 10：叉乘与外积的关系。图中红色部分表示单位法向量和“平行”的单位双向量。

　　 例如，力矩通常定义为垂直力分量的大小乘以距离，或者说是单位角度的功。 因此，由力 $F$ 产生的力矩（功 $W$ 随角度的变化率）为： $$ \tau = \frac{dW}{d\theta} = F \cdot \frac{d\mathbf{r}}{d\theta} = F \cdot (\mathbf{r} i).~ $$ 在三维向量分析中，旋转量通常使用叉乘表示。结合选定的有向体积元 $I$，可以通过以下对偶关系将其与几何代数中的外积联系起来，从而更自然地用双向量解释这些量： $$ a \times b = -I (a \wedge b).~ $$ 与传统的叉乘形式 $\tau = \mathbf{r} \times F$ 不同，几何代数中的力矩表示不会引入一个法向方向的额外向量：这种向量在二维中是不存在的；在高于三维的空间中也不是唯一的。在几何代数的表示中，单位双向量直接描述了旋转所在的平面及其方向，而旋转的方向（旋转的正负方向）则由向量 $\widehat{u}$ 和 $\widehat{v}$ 之间的夹角来决定。

5. 几何微积分

　　 几何微积分将几何代数的形式体系扩展到微分与积分，包括微分几何与微分形式的内容 \(^\text{[47]}\)。

　　 本质上，向量导数的定义是使几何代数版本的格林公式成立： $$ \int_{A} dA \, \nabla f = \oint_{\partial A} dx \, f~ $$ 由此，可以将导数写作几何乘积的形式： $$ \nabla f = \nabla \cdot f + \nabla \wedge f,~ $$ 从而有效地推广了斯托克斯定理（包括其微分形式版本）。在一维情况下，当 $A$ 是一个起点为 $a$，终点为 $b$ 的曲线时： $$ \int_{A} dA \, \nabla f = \oint_{\partial A} dx \, f~ $$ 化简为： $$ \int_{a}^{b} dx \, \nabla f = \int_{a}^{b} dx \cdot \nabla f = \int_{a}^{b} df = f(b) - f(a),~ $$ 这就是积分微积分基本定理。

　　 此外，几何微积分还发展出了向量流形的概念，以及几何积分理论，后者推广了传统的微分形式理论。

6. 历史

20 世纪之前

　　 几何与代数的联系最早可追溯到公元前 3 世纪欧几里得的《几何原本》（参见古希腊几何代数）。然而，本篇文章所指的几何代数（GA）直到 1844 年才真正发展起来，并被系统化地用于描述空间的几何性质与变换。在这一年，赫尔曼·格拉斯曼提出了几何代数的概念，将其定义为一种类似命题演算的计算体系，能够完整编码空间的几何信息。\(^\text{[48]}\) 格拉斯曼的代数体系可以应用于多种类型的空间，其中主要包括：欧几里得空间，仿射空间，射影空间；在格拉斯曼之后，1878 年，威廉·金登·克利福德在研究格拉斯曼代数的同时，将其与威廉·罗恩·哈密顿的四元数理论结合进行分析（Clifford 1878）。在克利福德看来：四元数描述的是某些变换（他称之为旋量 rotors）；而格拉斯曼代数描述的是空间的几何属性（如长度、面积和体积等 “Strecken”）。克利福德的主要贡献是：在现有的格拉斯曼代数上引入了一种新的运算——几何积，从而使四元数能够自然地嵌入该代数体系之中。随后在 1886 年，鲁道夫·利普希茨进一步推广了克利福德对四元数的解释，并将其应用于 $n$ 维空间中的旋转几何。这些发展最终为 20 世纪数学家们对克利福德代数的形式化和深入研究奠定了基础。

　　 然而，19 世纪的另一项革命性发展几乎完全掩盖了几何代数的光芒，那就是向量分析，由乔赛亚·威拉德·吉布斯和奥利弗·赫维赛德独立发展完成。向量分析的诞生，源于詹姆斯·克拉克·麦克斯韦在研究电磁学时的需求，特别是为了更简便地表达和处理某些偏微分方程。与新兴的几何代数的严格体系相比，向量分析更加直观易懂，因而迅速获得物理学家和数学家的青睐，并成为他们首选的几何工具。尤其是在 1901 年，埃德温·比德韦尔·威尔逊根据吉布斯的讲义出版了极具影响力的教科书《向量分析（Vector Analysis）》之后，向量分析的地位更是得到了广泛确立与普及。

　　 更具体地说，几何代数的发展经历了三条主要路径：四元数分析由哈密顿于 1843 年提出，并在 1878 年被克利福德几何化为旋量；几何代数由格拉斯曼于 1844 年提出；向量分析在 19 世纪末由吉布斯和赫维赛德从四元数分析发展而来。四元数分析在向量分析中的遗产，体现在 $\mathbf{R}^3$ 的基向量记作 $i$、$j$、$k$，这本质上把 $\mathbf{R}^3$ 看作 “纯虚数四元数” 的空间。从几何代数的角度来看：时空代数的偶子代数与三维欧几里得空间的几何代数是同构的四元数则与三维欧几里得空间几何代数的偶子代数同构。这种同构关系把这三条发展路径统一在同一个理论框架下。

20 世纪至今

　　 在整个 20 世纪，克利福德代数的研究一直在默默推进，这主要得益于抽象代数学家如埃利·卡当、赫尔曼·外尔和克洛德·谢瓦莱等人的工作。几何化方法的几何代数在 20 世纪经历了多次复兴：数学领域，埃米尔·阿廷的著作《Geometric Algebra》\(^\text{[49]}\) 讨论了与多种几何（如仿射几何、射影几何、辛几何和正交几何）相关的代数结构。物理领域，几何代数作为一种 “新的” 数学工具重新被引入，用于处理经典力学和电磁学，并扩展到量子力学、规范理论等更复杂的主题。\(^\text{[5]}\) 大卫·赫斯特尼斯重新诠释了泡利矩阵和狄拉克矩阵，分别将其视为空间和时空中的向量，并成为推动几何代数现代应用的主要倡导者之一。

　　 计算机图形学与机器人学，几何代数被重新用于高效表示旋转和其他变换。在机器人学（螺旋理论、利用向量乘子的运动学与动力学）、计算机视觉、控制以及神经计算（几何学习）等领域，几何代数的应用得到了广泛探索（参见 Bayro 2010）。

7. 参见

8. 注释

　　
a.“通用” 代数指的是满足所有定义方程的最 “完整” 或最不退化的代数。在本文中，“克利福德代数” 指的就是通用克利福德代数。

b.在几何代数中，术语内积是指 1-向量子空间上的对称双线性形式，等价于伪欧几里得向量空间中的标量积，而不是赋范向量空间中的内积。一些作者可能将内积的概念扩展到整个代数，但在这一点上并没有统一共识。即使在几何代数相关的著作中，这个术语也并非普遍采用。
c.内积的定义条件也可以替换为以下之一 \(^\text{[11][12]}\)：任意一组线性无关向量的乘积不能落在标量域 $F$ 内，或代数的维度必须是 $2^{\dim V}$。
d.几何代数中使用的术语外积与数学其他领域中 “外积” 一词的含义不一致。
e.已知 $u^2 = 1$，则有：$\left(\tfrac{1}{2}(1+u)\right)^2 = \tfrac{1}{4}(1 + 2u + uu)= \tfrac{1}{4}(1 + 2u + 1)= \tfrac{1}{2}(1+u)$,这表明 $\tfrac{1}{2}(1+u)$ 是幂等元。并且：$\tfrac{1}{2}(1+u)(1-u)= \tfrac{1}{2}(1 - uu)= \tfrac{1}{2}(1 - 1)= 0$,这说明它是一个非零零因子。
f.“级” 是指代数在外积下的分级结构（即 $\mathbb{Z}$-分级）中，同类齐次元素的 “次数”，而不是指在几何乘积下的分级。
g.Hestenes “复兴并适度推广了 Hamilton 四元数演算中的一个已废弃术语”，将 $k$-向量乘子定义为可以分解为 $k$ 个向量乘积的多向量。\(^\text{[20]}\)
h.只有保持双线性形式的线性变换的外延映射才符合这种描述；而一般情况下，外延映射并不能直接通过代数运算来表示。
i.“[…] 外积运算与并关系本质上具有相同的含义。格拉斯曼–凯莱代数将交关系视为其对应概念，并提供了一个统一的框架，使这两种运算能够在同一层级上被处理 […]格拉斯曼本人将交运算定义为外积的对偶运算，但后来的数学家通过一种称为 shuffle 的过程，独立于外积定义了交运算，因此该交运算也被称为 shuffle 乘积。研究表明，这是一种反对称运算，并且满足结合律，从而形成了一种独立的代数结构。因此，格拉斯曼–凯莱代数实际上同时具备两种代数结构：一种基于外积（或并 join）；另一种基于 shuffle 乘积（或交 meet）。因此，这一结构也被称为 “双代数”，并且这两种结构互为对偶。\(^\text{[26]}\)”
j.这不应与 Hestenes 的不规则广义定义混淆：$C \bullet_{\text{H}} D := \sum_{r \neq 0, s \neq 0} \left\langle \langle C \rangle_{r} \langle D \rangle_{s} \right\rangle_{|s-r|}$ 其中，这种区分性的符号来自 Dorst、Fontijne 和 Mann（2007，第 590 页，附录 B.1），强调在这种乘积下必须单独处理标量分量。
k.通常还会附加条件：$\underline{\mathsf{f}}(1) = 1$ 以确保零映射的唯一性。 l.该定义遵循 Dorst、Fontijne 和 Mann（2007）以及 Perwass（2009）的工作——Dorst 使用的左收缩取代了 Perwass 所用的 “粗点” 内积，这与 Perwass 所提出的 “向量 $A$ 的级别不能超过 $B$ 的级别” 的约束保持一致。
m.Dorst 似乎只是直接假定存在 $B^{+}$，使得：$B \;\rfloor\; B^{+} = 1$,而 Perwass（2009）则明确给出了定义：$B^{+} =B^{\dagger}/(B \;\rfloor\; B^{\dagger})$,其中 $B^{\dagger}$ 是 $B$ 的共轭，这与 $B$ 的逆序仅差一个符号。
n.也就是说，投影必须定义为：$\mathcal{P}_{B}(A) = (A \;\rfloor\; B^{+}) \;\rfloor\; B$,而不能写作：$(A \;\rfloor\; B) \;\rfloor\; B^{+}$,尽管对于非零刃 $B$ 来说，这两者是等价的。

9. 参考文献

  1. Hestenes 1986，第 6 页
  2. Li 2008，第 411 页
  3. Hestenes 1966
  4. Hestenes 2003
  5. Doran 1994
  6. Lasenby, Lasenby & Doran 2000
  7. Hildenbrand 等，2004
  8. Hestenes & Sobczyk 1984，第 3–5 页
  9. Aragón, Aragón & Rodríguez 1997，第 101 页
  10. Lounesto 2001，第 190 页
  11. Lounesto 2001，第 191 页
  12. Vaz & da Rocha 2016，第 58 页，定理 3.1
  13. Hestenes 2005
  14. Penrose 2007
  15. Wheeler, Misner & Thorne 1973，第 83 页
  16. Wilmot 1988a，第 2338 页
  17. Wilmot 1988b，第 2346 页
  18. Chevalley 1991
  19. Wilmot 2023
  20. Hestenes & Sobczyk 1984，第 103 页
  21. Dorst, Fontijne & Mann 2007，第 204 页
  22. Dorst, Fontijne & Mann 2007，第 177–182 页
  23. Lundholm & Svensson 2009，第 58 页及后续内容
  24. Lundholm & Svensson 2009，第 58 页
  25. Francis & Kosowsky 2008
  26. Kanatani 2015，第 112–113 页
  27. Dorst & Lasenby 2011，第 443 页
  28. Vaz & da Rocha 2016，第 2.8 节
  29. Hestenes & Sobczyk 1984，第 31 页
  30. Doran & Lasenby 2003，第 102 页
  31. Dorst & Lasenby 2011，序言第 vi 页
  32. Electromagnetism using Geometric Algebra versus Components，检索于 2013-03-19
  33. Selig 2005
  34. Hadfield & Lasenby 2020
  35. Projective Geometric Algebra，projectivegeometricalgebra.org，检索于 2023-10-03
  36. Hrdina, Návrat & Vašík 2018
  37. Lengyel 2024
  38. Wu 2022
  39. Sokolov 2013
  40. Lasenby 2004
  41. Dorst 2016
  42. Perwass 2009
  43. Breuils 等，2019
  44. Easter & Hitzer 2017
  45. Dorst, Fontijne & Mann 2007，第 3.6 节，第 85 页
  46. Perwass 2009，第 3.2.10.2 节，第 83 页
  47. Hestenes & Sobczyk 1984
  48. Grassmann 1844
  49. Artin 1988

10. 参考文献与延伸阅读

11. 外部链接

　　 早期文献与研究

　　 研究团体与资源

                     

© 保留一切权利