抽象代数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：魔方的所有排列构成一个群，这是抽象代数中的一个基本概念。

　　 在数学中，更具体地说，在代数学中，抽象代数或现代代数是研究代数结构的学科。代数结构是指带有特定运算作用于其元素的集合。\(^\text{[1]}\) 代数结构包括群、环、域、模、向量空间、格以及域上的代数。抽象代数这一术语是在 20 世纪早期提出的，用来将其与代数学的旧分支区分开来，更具体地，是为了区别于初等代数，即使用变量来表示数进行计算和推理的部分。如今，抽象的代数观点已成为高等数学中如此根本的内容，以至于通常直接称为 “代数”，而 “抽象代数” 这一术语除了在教学中很少再被使用。

　　 代数结构及其相关的同态构成数学上的范畴。范畴论提供了一个统一的框架，用来研究各种结构中类似的性质和构造。

　　 一般代数是一个相关学科，研究将不同类型的代数结构作为单一对象来对待。例如，在一般代数中，群的结构是一个单一的对象，被称为群的多类。

1. 历史

　　 在 19 世纪之前，代数被定义为对多项式的研究。\(^\text{[2]}\) 随着更复杂的问题和解法的发展，抽象代数在 19 世纪逐渐产生。具体的问题和例子来自数论、几何、分析以及代数方程的解。如今被认为是抽象代数组成部分的大多数理论，最初只是来自数学各个分支的一些零散事实的集合，随后逐渐形成了一个共同的主题，作为核心将各种结果汇集起来，并最终在一套共同概念的基础上实现统一。这种统一发生在 20 世纪的前几十年，促成了对群、环、域等各种代数结构的形式公理化定义。\(^\text{[3]}\) 这一历史发展过程几乎与流行教材中的处理方式相反，例如范德瓦尔登的 《现代代数》\(^\text{[4]}\)，这些教材通常在每一章开头给出某种结构的形式定义，然后再给出具体的实例。\(^\text{[5]}\)

初等代数

　　 对多项式方程或代数方程的研究有着悠久的历史。大约公元前 1700 年，巴比伦人已经能够解出以文字题形式给出的二次方程。这个 “文字题” 阶段被称为修辞代数，并且一直到 16 世纪都是主流方法。公元 830 年，花拉子米首次提出 “algebra（代数）” 一词，但他的工作完全属于修辞代数。完全符号化的代数直到弗朗索瓦·维埃特 1591 年的《新代数》才出现，即便如此，其中仍有一些拼写出的词语，直到笛卡尔 1637 年的《几何学》才被赋予统一的符号表示。\(^\text{[6]}\) 对符号方程求解的正式研究促使莱昂哈德·欧拉在 18 世纪末接受当时被认为是 “荒谬” 的根，例如负数和虚数。\(^\text{[7]}\) 然而，大多数欧洲数学家直到 19 世纪中叶仍然抗拒这些概念。\(^\text{[8]}\)

　　 乔治·皮考克 1830 年的《代数论》是第一次尝试将代数完全建立在严格的符号基础之上。他区分了新的符号代数与旧的算术代数。在算术代数中，$a - b$ 被限制为 $a \geq b$，而在符号代数中，所有的运算规则在没有任何限制的情况下成立。利用这一点，皮考克能够证明类似 $(-a)(-b) = ab$ 这样的法则：只需令 $a = 0,\ c = 0$ 代入 $(a - b)(c - d) = ac + bd - ad - bc$ 即可成立。皮考克使用他称为等价形式永久性原理来为他的论证辩护，但他的推理存在归纳法问题。\(^\text{[9]}\) 例如，$\sqrt{a}\sqrt{b} = \sqrt{ab}$ 对于非负实数成立，但对一般复数却不成立。

早期群论

　　 数学的几个领域共同促成了对群的研究。拉格朗日 1770 年对五次方程解的研究，促成了多项式的伽罗瓦群的诞生。高斯 1801 年对费马小定理的研究引出了模 $n$ 的整数环、模 $n$ 的整数乘法群，以及更一般的循环群和阿贝尔群的概念。克莱因 1872 年的埃尔朗根纲领研究几何学，并引出了对称群，例如欧几里得群和射影变换群。1874 年，李引入了李群理论，旨在发展 “微分方程的伽罗瓦理论”。1876 年，庞加莱和克莱因引入了莫比乌斯变换群，以及它的子群，例如模群和 Fuchs 群，其基础是分析中自守函数的研究。\(^\text{[10]}\)

　　 群的抽象概念在 19 世纪中叶缓慢发展起来。1832 年，伽罗瓦首次使用 “群” 一词 \(^\text{[11]}\)，表示在复合运算下封闭的一个置换集合。\(^\text{[12]}\) 阿瑟·凯莱 1854 年的论文《论群论》将群定义为一个带有结合性复合运算和单位元 $1$ 的集合，这在今天被称为幺半群。\(^\text{[13]}\)1870 年，克罗内克定义了一种抽象的二元运算，该运算是封闭的、交换的、结合的，并且具有左消去性质 $b \neq c \to a \cdot b \neq a \cdot c$\(^\text{[14]}\) 类似于有限阿贝尔群的现代运算规律。\(^\text{[15]}\) 韦伯 1882 年对群的定义是一个封闭的二元运算，它满足结合律并具有左右消去性。\(^\text{[16]}\)1882 年，沃尔特·冯·迪克首次要求逆元必须作为群定义的一部分。\(^\text{[17]}\)

　　 一旦抽象群的概念形成，各种结果就被重新用这种抽象框架加以表述。例如，西罗定理在 1887 年被弗罗贝尼乌斯直接根据有限群的运算规律重新证明，尽管弗罗贝尼乌斯指出该定理可由关于置换群的柯西定理以及 “每个有限群都是某个置换群的子群” 这一事实推出。\(^\text{[18][19]}\) 奥托·赫尔德在这一领域尤为高产：他在 1889 年定义了商群，1893 年定义了群自同构以及单群，并且完成了约旦–赫尔德定理。德德金和米勒独立地刻画了哈密顿群并引入了两个元素的换子的概念。伯恩赛德、弗罗贝尼乌斯和莫利安（Molien）在 19 世纪末建立了有限群的表示论。\(^\text{[18]}\)J. A. de Séguier 1905 年的专著《抽象群论要素》以抽象、一般的形式呈现了其中许多成果，把 “具体的” 群 relegated 到附录中，尽管它仅限于有限群。第一本关于有限与无限抽象群的专著是 O. K. Schmidt 1916 年的《抽象群论》。\(^\text{[20]}\)

早期环论

　　 非交换环论起始于将复数扩展为超复数，尤其是威廉·罗恩·哈密顿在 1843 年提出的四元数。不久之后，许多其他数系陆续出现。1844 年，哈密顿提出双四元数，凯莱引入了八元数，格拉斯曼引入了外代数。[21] 1848 年，詹姆斯·科克尔提出四维复数，[22] 1849 年提出共四元数。[23] 威廉·金登·克利福德在 1873 年引入了分裂双四元数。此外，凯莱在 1854 年引入了实数和复数上的**群代数，并在 1855 年和 1858 年的两篇论文中引入了方阵。[24]

　　 当足够多的例子被发现后，下一步就是对它们进行分类。在 1870 年的一部专著中，本杰明·皮尔斯对维数低于 6 的 150 多种超复数系进行了分类，并给出了结合代数的明确定义。他定义了幂零元和幂等元，并证明了任何代数必定包含其中之一。他还定义了皮尔斯分解。弗罗贝尼乌斯在 1878 年和查尔斯·桑德斯·皮尔斯在 1881 年独立证明，唯一的有限维除环是 $\mathbb{R}$ 上的实数、复数和四元数。在 1880 年代，基林和埃利·卡当证明了半单李代数可以分解为若干个单李代数，并对所有单李代数进行了分类。受此启发，在 1890 年代，卡当、弗罗贝尼乌斯和莫利安独立证明：有限维结合代数在 $\mathbb{R}$ 或 $\mathbb{C}$ 上可以唯一分解为一个幂零代数和一个半单代数的直和，后者是若干个单代数的乘积，而这些单代数是除代数上的方阵代数。卡当是第一个定义直和和单代数概念的人，而这些概念后来证明影响极大。在 1907 年，韦德伯恩将卡当的结果推广到任意域，这些结果如今被称为韦德伯恩主定理和阿廷–韦德伯恩定理。[25]

　　 对于交换环，多个领域的研究共同促成了交换环理论的发展。[26] 高斯在 1828 年和 1832 年的两篇论文中提出了高斯整数，并证明它们构成一个唯一分解整环，同时证明了双二次互反律。大约在同一时期，雅可比和艾森斯坦为艾森斯坦整数证明了三次互反律。[25]

　　 对费马大定理的研究引出了代数整数。1847 年，加布里埃尔·拉梅曾认为自己证明了 FLT，但他的证明是错误的，因为他假设所有圆分域都是 UFD。然而，正如库默尔所指出的，$\mathbb{Q}(\zeta_{23})$ 并不是一个 UFD。[27] 在 1846 年和 1847 年，库默尔引入了理想数，并证明了圆分域中对理想素数的唯一分解性。[28] 德德金在 1871 年推广了这一结果，证明了代数数域的整数环中任一非零理想可以唯一分解为若干素理想的乘积，这是德德金整环理论的前身。总体而言，德德金的工作奠定了代数数论这一学科。[29]

　　 在 1850 年代，黎曼引入了黎曼曲面的基本概念。黎曼的方法依赖于他称之为狄利克雷原理的假设，[30] 但在 1870 年被魏尔斯特拉斯提出质疑。很久以后，在 1900 年，希尔伯特通过发展变分法中的直接方法，为黎曼的方法提供了严谨的依据。[31]在 1860 年代和 1870 年代，克莱布施、戈尔丹、布里尔，尤其是 M. 诺特（M. Noether）研究了代数函数和代数曲线。尤其是诺特研究了一个多项式成为多项式环 $\mathbb{R}[x,y]$ 中由两条代数曲线生成的理想的元素所需的条件，尽管诺特当时并未使用这种现代语言。1882 年，德德金和韦伯类比德德金早期在代数数论中的工作，创建了代数函数域理论，从而首次给出了黎曼曲面的严格定义，并严格证明了黎曼–罗赫定理。克罗内克在 1880 年代、希尔伯特在 1890 年、拉斯克在 1905 年以及麦考莱在 1913 年进一步研究了隐含在 E. 诺特工作中的多项式环的理想结构。拉斯克证明了拉斯克–诺特定理的一个特殊情形，即多项式环中的每个理想都是有限个初等理想的交集；麦考莱则证明了这种分解的唯一性。[32]总体而言，这些工作推动了代数几何的发展。[26]

　　 1801 年，高斯引入了整数上的二次二元型并定义了它们的等价关系。他进一步定义了这些型的判别式，这是二元型的不变量。1860 年代至 1890 年代之间，不变量理论逐渐发展并成为代数学的一个主要领域。凯莱、西尔维斯特、戈尔丹等人找到了雅可比行列式和黑塞行列式，用于处理二元四次型和三次型。[33] 1868 年，戈尔丹证明了复数域上一个二元型的不变量的分次代数是有限生成的，即它有一个基。[34] 希尔伯特在 1885 年写了一篇关于不变量的论文，并在 1890 年证明了任何次数或任意变量数的型都有一个基。他进一步在 1890 年推广这一结果，提出了著名的希尔伯特基定理。[35]

　　 这些理论建立之后，直到几十年后抽象的环概念才逐渐出现。第一次公理化的定义是亚伯拉罕·弗兰克尔在 1914 年给出的。[35] 他的定义主要是标准的公理：一个集合带有两个运算——加法，其构成一个群（不一定交换），以及乘法，其满足结合律、对加法的分配律并且具有单位元。[36] 此外，他还提出了关于 “正则元” 的两个公理，这些公理受到关于 $p$ 进数（$p$-adic numbers）研究的启发，但排除了现今常见的环，如整数环。这些公理使得弗兰克尔能够证明加法是交换的。[37] 弗兰克尔的工作旨在将施泰尼茨 1910 年对域的定义推广到环上，但它与已有的关于具体系统的研究没有关联。园正三 1917 年的定义是第一个等价于现今定义的环的定义。[38]

　　 1920 年，埃米·诺特与 W. Schmeidler 合作发表了一篇关于理想理论的论文，其中他们在环中定义了左理想和右理想。次年，她发表了一篇划时代的论文《环域中的理想理论》，分析了与（数学）理想相关的升链条件。这篇论文产生了 “诺特环” 一词，以及其他多个被称为 “诺特型” 的数学对象。[39][40] 著名代数学家卡普兰斯基称这项工作是 “革命性的”；[39] 许多看似与多项式环性质紧密联系的结果被证明仅从一个公理便可推出。[41] 阿廷受到诺特工作的启发，提出了降链条件。这些定义标志着抽象环论的诞生。[42]

早期域论

　　 1801 年，高斯引入了模 $p$ 的整数，其中 $p$ 是一个质数。1830 年，伽罗瓦将其推广到具有 $p^n$ 个元素的有限域。[43] 1871 年，理查德·德德金提出，对于一个在四则运算下封闭的实数或复数集合，[44] 使用德语词 Körper（意为 “身体” 或 “整体”），以暗示一个有机封闭的实体。英语术语 “field（域）” 是摩尔在 1893 年引入的。[45]1881 年，利奥波德·克罗内克定义了他称之为有理性域的概念，在现代术语中即为有理分式域。[46] 第一个明确的抽象域定义是海因里希·马丁·韦伯在 1893 年提出的。该定义缺少了乘法的结合律，但涵盖了有限域以及代数数论和代数几何中的域。[47]1910 年，施泰尼茨综合了迄今为止积累的抽象域论知识。他以公理化方式给出了现代定义下的域，按特征数对它们进行了分类，并证明了许多如今常见的定理。[48]

其他主要领域

现代代数

　　 19 世纪末至 20 世纪初，数学的方法论发生了转变。抽象代数在 20 世纪初逐渐兴起，当时被称为现代代数。它的研究是推动数学具有更高逻辑严谨性的努力的一部分。最初，古典代数中的假设——整个数学（以及自然科学的主要部分）都依赖于此——采取了公理化系统的形式。数学家们不再满足于建立具体对象的性质，而是开始将注意力转向一般理论。对某些代数结构的形式化定义在 19 世纪开始出现。例如，各种置换群的研究结果逐渐被视为关于抽象群一般概念的通用定理的具体实例。对各种数学对象的结构和分类问题成为研究的焦点。[50]

　　 这些过程贯穿于整个数学领域，但在代数中尤为显著。通过基本运算和公理给出形式化定义的方法被应用于许多基本的代数结构，如群、环和域。因此，群论和环论等逐渐在纯数学中占据一席之地。埃尔恩斯特·施泰尼茨对一般域的代数研究、戴维·希尔伯特、埃米尔·阿廷和埃米·诺特对交换环及一般环的代数研究，建立在埃尔恩斯特·库默尔、利奥波德·克罗内克和理查德·德德金的工作之上，这些学者研究了交换环中的理想；同时乔治·弗罗贝尼乌斯和伊赛·舒尔对群的表示论也作出了重要贡献。这些成果共同塑造了抽象代数的框架。19 世纪最后四分之一和 20 世纪最初四分之一的发展，系统地呈现在巴特尔·范德瓦尔登的《现代代数》中。这部两卷本专著于 1930–1931 年出版，将代数的研究方向从方程理论重新定位到代数结构理论。[51]

2. 基本概念

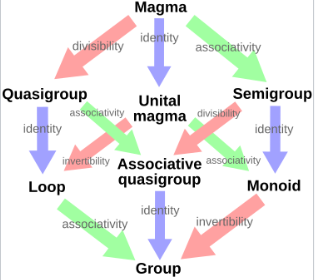
　　 通过抽象掉不同层次的细节，数学家们定义了许多代数结构，这些结构被应用于数学的各个领域。例如，几乎所有被研究的系统都是**集合（sets）**，因此它们满足集合论的定理。在这些集合中，如果定义了一种二元运算，就形成了**幺半群（magmas）**，因此关于幺半群的概念和关于集合的概念都适用。我们可以对代数结构施加额外的约束，例如**结合性（associativity）**（从而形成**半群（semigroups）**）；单位元（identity）和逆元（inverses）（从而形成**群（groups）**）；以及其他更复杂的结构。随着附加结构的增加，可以证明更多的定理，但一般性（generality）会降低。代数对象的 “**层次结构（hierarchy）**”（以一般性为衡量）会产生相应理论的层次结构：例如，在研究\*\*环（rings）**时（环是带有某些公理的两个二元运算的代数对象），可以使用**群论（group theory）\*\*的定理，因为一个环在其中一个运算下是一个群。总体而言，一般性与理论的丰富性之间存在平衡：更一般的结构通常具有更少的非平凡定理和更少的应用。

图
图 2：介于幺半群和群之间的代数结构。例如，幺半群是带有单位元的半群。

　　 具有单一二元运算的代数结构示例有：

　　 包含多个运算的示例有：

3. 抽象代数的分支

群论

　　 一个群是一个集合 $G$ 以及一个 “群乘法）”，即一个二元运算 $\cdot : G \times G \rightarrow G$。该群满足以下定义公理（参见 Group (mathematics) § Definition）：

　　 单位元：存在一个元素 $e$ 使得对每个 $a \in G$ 都有 $e \cdot a = a \cdot e = a$。

　　 逆元：对每个 $a \in G$ 存在一个元素 $b$ 使得 $a \cdot b = b \cdot a = e$。

　　 结合性：对每个 $a,b,c \in G$ 都有 $(a \cdot b) \cdot c = a \cdot (b \cdot c)$。

环论

　　 一个环是一个集合 $R$ 配备了两个二元运算：加法：$(x,y) \mapsto x + y$，乘法：$(x,y) \mapsto xy$。 满足以下公理：

4. 应用

　　 由于其高度的普适性，抽象代数被应用于数学和科学的许多领域。例如，代数拓扑使用代数对象来研究拓扑空间。2003 年被证明的庞加莱猜想断言：流形的基本群可以用来确定该流形是否为一个球面，该基本群编码了连通性的信息。代数数论研究各种推广整数集的数环。利用代数数论的工具，安德鲁·怀尔斯证明了费马大定理。

　　 在物理学中，群用于表示对称操作，使用群论可以简化微分方程。在规范理论中，对局域对称性的要求可以用来推导描述系统的方程。描述这些对称性的群是李群，而研究李群和李代数可以揭示许多关于物理系统的重要信息。例如，在一个理论中，力的载体的数目等于其李代数的维度；如果李代数是非阿贝尔的，这些玻色子会与它们所介导的力相互作用。[52]

5. 参见

6. 参考文献

  1. Finston, David R.; Morandi, Patrick J. (2014 年 8 月 29 日). *《抽象代数：结构与应用》。Springer 出版社，第 58 页。ISBN 978-3-319-04498-9。我们对抽象代数的研究大多涉及对结构及其运算的分析。
  2. Kleiner 2007，第 1 页。
  3. Kleiner 2007，第 xi–xii 页。
  4. van der Waerden, Bartel Leendert (1949). 《现代代数》。第 I 卷。Fred Blum 翻译。纽约：Frederick Ungar Publishing Co. MR 0029363。
  5. Kleiner 2007，第 41 页。
  6. Kleiner 2007，第 1–13 页。
  7. Euler, Leonard (1748). *《无穷分析导论（拉丁文）。第 1 卷。瑞士卢塞恩：Marc Michel Bosquet & Co. 第 104 页。
  8. Martinez, Alberto (2014). 《负数数学》。Princeton University Press，第 80–109 页。
  9. Kleiner 2007，第 13–14 页。
  10. Kleiner 2007，第 17–22 页。
  11. O'Connor, John J.; Robertson, Edmund F.，“抽象群概念”，圣安德鲁斯大学 MacTutor 数学史档案。
  12. Kleiner 2007，第 23 页。
  13. Cayley, A. (1854). “论群论及其符号方程 $\theta^n = 1$ 的依赖关系（On the theory of groups, as depending on the symbolic equation $\theta^n = 1$）”。《哲学杂志》，第 4 系列，7 (42): 40–47。doi:10.1080/14786445408647421。
  14. Kronecker, Leopold (1895). “一些理想复数类数性质的说明”。见 Hensel, Kurt (编). 《利奥波德·克罗内克全集：由普鲁士科学院委托出版。莱比锡、柏林：B.G. Teubner 出版社，第 275 页。
  15. Kleiner 2007，第 27 页。
  16. Kleiner 2007，第 32 页。
  17. Kleiner 2007，第 33 页。
  18. Kleiner 2007，第 34 页。
  19. Frobenius, G. (2008 年 4 月) [1887]. “Sylow 定理的新证明”。《纯粹与应用数学杂志》（德文）。1887 (100)。由 Gutfraind, Sasha 翻译：179–181。doi:10.1515/crll.1887.100.179。S2CID 117970003。
  20. Kleiner 2007，第 35 页。
  21. Kleiner 2007，第 42–43 页。
  22. Cockle, James (1848). “关于一些类似四元数的函数及代数中的一种新虚数”。《伦敦、爱丁堡与都柏林哲学杂志及科学期刊》，第 33 卷。Taylor & Francis 出版社：435–439 页。doi:10.1080/14786444808646139。
  23. Cockle, James (1849). “关于涉及多于一个虚数的代数系统”。《伦敦、爱丁堡与都柏林哲学杂志及科学期刊》，第 35 卷。Taylor & Francis 出版社：434–437 页。doi:10.1080/14786444908646384。
  24. Kleiner 2007，第 43 页。
  25. Kleiner 2007，第 43–47 页。
  26. Kleiner 2007，第 42 页。
  27. Kleiner 2007，第 48 页。
  28. Kleiner 2007，第 50 页。
  29. Kleiner 2007，第 51–52 页。
  30. Kleiner 2007，第 54 页。
  31. Monna 1975，第 55–56 页，引用 Hilbert, David (1905)，“关于狄利克雷原理”，《纯粹与应用数学杂志》（德文），第 129 卷，第 63–67 页。
  32. Kleiner 2007，第 54–57 页。
  33. Kleiner 2007，第 57–58 页。
  34. Gordan, Paul (1868)，“证明：二元型的每个协变式与不变量都是有限个此类型的系数为数值的整函数”，《纯粹与应用数学杂志》，1868 年，第 69 期，第 323–354 页，doi:10.1515/crll.1868.69.323，S2CID 120689164。
  35. Kleiner 2007，第 58 页。
  36. Frankel, A. (1914)，“关于零因子与环的分解”，J. Reine Angew. Math.，第 145 卷，第 139–176 页。
  37. Corry, Leo (2000 年 1 月)，“抽象环定义的起源”，Modern Logic，8 (1–2)：5–27。ISSN 1047-5982。
  38. Kleiner 2007，第 58–59 页。
  39. Kimberling 1981，第 18 页。
  40. Dick, Auguste (1981)，《埃米·诺特：1882–1935》，H. I. Blocher 翻译，Birkhäuser 出版社，ISBN 3-7643-3019-8，第 44–45 页。
  41. Kleiner 2007，第 59 页。
  42. Kleiner 2007，第 60 页。
  43. Kleiner 2007，第 70 页。
  44. Kleiner 2007，第 66 页。
  45. “数学中某些词汇最早已知用法”。
  46. Kleiner 2007，第 67 页。
  47. Kleiner 2007，第 72–73 页。
  48. Kleiner 2007，第 74–76 页。
  49. Hart, Roger (2011). 《线性代数的中国根源》。马里兰州巴尔的摩：约翰斯·霍普金斯大学出版社。ISBN 978-0-8018-9958-4。OCLC 794700410。
  50. Gray, Jeremy (2018). 《抽象代数史：从代数方程到现代代数》。Springer 本科数学系列，Springer Cham。doi:10.1007/978-3-319-94773-0。ISBN 978-3-319-94772-3。2025 年 2 月 10 日检索。
  51. Corry, Leo. “结构代数”。大英百科全书。2024 年 12 月 16 日存档。2025 年 2 月 10 日检索。 1930 年出版了一本教材，展示了该学科全新的形象。这本书是荷兰数学家 Bartel van der Waerden 的《现代代数》。自 1924 年以来，他曾在德国哥廷根听埃米·诺特的课，在汉堡听埃米尔·阿廷的课。van der Waerden 对该学科的新阐释颠倒了古典代数的概念层次结构。群、域、环以及其他相关概念成为研究的核心，因为它们都是某种更一般的、潜在的概念——代数结构的实例。
  52. Schumm, Bruce (2004). 《深层事物》。巴尔的摩：约翰斯·霍普金斯大学出版社。ISBN 0-8018-7971-X。

参考书目

7. 延伸阅读

8. 外部链接

                     

© 保留一切权利