树形动态规划
贡献者: 有机物
树形 $\texttt{dp}$ 顾名思义就是在树上做 $\texttt{dp}$。通常是从根节点开始遍历整棵树,在回溯的时候从子节点往上更新父节点的信息。对于特殊的节点,如根节点或叶子节点需要进行特殊的处理。因为树的遍历需要用到递归,所以树形 $\texttt{dp}$ 一般是根据递归实现的。所以树形 $\texttt{dp}$ 较为抽象,可以画图理解。
树形 $\texttt{dp}$ 的框架:
void dfs(int u, int father) // father 是 u 节点的父节点
{
for (int i = h[u]; ~i; i = ne[i]) // 遍历每条边
{
int j = e[i];
if (j == father) continue; // 如果是双向边需要特判,不往回重复搜索
dfs(j); // 递归搜索
f[j] <-- f[u] // 回溯的时候,用子节点更新父节点
}
}
简化题意:有 $n$ 节点构成一课树,每个节点有一个值 $w_i$,要求整棵树的权值最大值,如果一个节点的父节点加进了答案,那么这个节点就不能加进答案。
这是一个树的模型,因此可以通过树形 $\texttt{dp}$ 来求解。
- 状态表示:
(1):$f(u, 0)$:表示从 $u$ 的子树中选,且不选 $u$ 的子节点权值最大值。
(2):$f(u, 1)$:表示从 $u$ 的子树中选,且选择 $u$ 的子节点权值最大值。
- 状态计算:
(1):$f(u, 0) = \sum_{s_i \in \text{son}(u)} \max(f(s_i, 0), f(s_i, 1))$
(2):$f(u, 1) = \sum_{s_i \in \text{son}(u)} f(s_i, 0)$
因为没选 $u$ 这个节点,那么子节点可选可不选,因此求两者的最大值,如果选择了 $u$ 这个节点,那么子节点一定不能选。
每次 $\texttt{dfs}$ 的时候初始化每个节点的 $f(u, 1) = w_u$,从下往上递归计算,递归结束的时候,根节点就是答案。可见树形 $\texttt{dp}$ 的状态转移方程不止 $1$ 个,通常需要分类讨论。
时间复杂度:$\mathcal{O}(n)$。
C++ 代码:
void dfs(int u)
{
f[u][1] = w[u]; // 初始化每个节点选择自己的权值
for (int i = h[u]; ~i; i = ne[i]) // 遍历 u 的每条边
{
int j = e[i];
dfs(j);
f[u][1] += f[j][0]; // 选择 u
f[u][0] += max(f[j][1], f[j][0]); // 不选 u
}
return; // 回溯
}
简化题意:树中包含 $n$ 个结点和 $n-1$ 条无向边,每条边都有一个权值。换句话说,要找到一条路径,使得使得路径两端的点的距离最远,这条路径就被称为是树的直径。路径中可以只包含一个点。
对于没有边权的树的来说,它的最长路径就是最长边数的路径,做法是任取一点作为起点,然后找到以这个点最远的一个点 $u$,在从 $u$ 这个点找到一个距离它最远的一个点 $v$,则 $u$ 到 $v$ 这条路径就是最长路径,而对于有权树,需要用树形 $\tt dp$ 解决。
- 状态表示:$f_u$ 表示经过 $u$ 的一条最长路径。
- 状态计算:
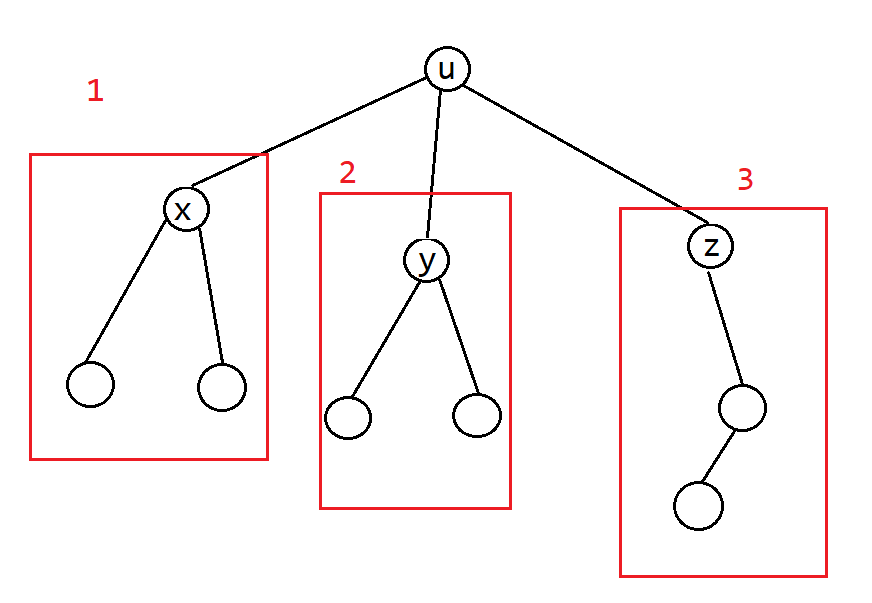
(1):以 $u$ 为根的路径有好几条,$d_1 = f(x) + w(u \to x)$。
(2):$d_2 = f_y + w(u \to y)$。
表示经过 $u$ 的一条最长路径必然经过以下三个区域的其中一个区域,因此有:
因为要求最大值,所以求一条最长路径和一条次长路径就行了,不一定非得选 $2$ 条路径,因为有些路径的权值之和可能为负数,但是最优解的路径一定是 $2$ 条。
最大值和次大值需要初始化为 $0$,因为如果边权为负数,可以选一个点,答案为 $0$。
状态计算过程中的 $f_x$ 表示以 $x$ 为根的子树中最长的一条路径,不是经过 $u$ 的一条最长路径。所以状态计算中的两条路径(一条最长边和一条次长边)加起来就是经过 $u$ 的一条最长路径。
本题的答案不一定为以 $u$ 为顶点的路径,因为 $u$ 到其他点的距离可能均为负数,所以答案可以是以其他点顶点的路径,本题采用 $\tt dfs$ 递归的方法 来求解,所以是求解方式自下而上的。
时间复杂度:$\mathcal{O}(n)$。
C++ 代码:
const int N = 10010, M = N * 2;
int n, h[N], e[M], w[M], ne[M], idx, ans;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dfs(int u, int father)
{
int dist = 0; // 表示从当前点往下走的最大长度
int d1 = 0, d2 = 0; // d1 最长路径,d2 次长路径
int d = 0;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
d = dfs(j, u) + w[i];
dist = max(dist, d); // f[x]
if (d >= d1) d2 = d1, d1 = d;
else if (d > d2) d2 = d;
}
ans = max(ans, d1 + d2);
return dist;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << ans << endl;
return 0;
}
前面的题目都是比较容易可以看出来是树形 $\texttt{dp}$,让我们看看怎么将一个具体的题目抽象成树形 $\texttt{dp}$。
数字转换 题意:如果一个数 $x$ 的约数之和 $y$(不包括他本身)比他本身小,那么 $x$ 可以变成 $y$,$y$ 也可以变成 $x$。例如,$4$ 可以变为 $3$,$1$ 可以变为 $7$。
限定所有数字变换在不超过 $n$ 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
做法:如果一个数 $x$ 的约数之和 $y$(不包括他本身)比他本身小,那么就从 $y$ 向 $x$ 连一条有向边。注意顺序不能颠倒,因为一个数仅有一个约数之和,但一个约数之和可以对应着很多数。例如 $2$ 和 $3$ 的约数之和都是 $1$,若从数向约数之和连边的话,这样某些结点就不止有一个父节点了,这样连就不一定是树了。
这样将树建好之后,问题转化为树的直径问题,求一个最长直径即可。
由于题目中可能会存在多棵树,因此需要将每个点都 dfs 一遍。
遍历的时候可以不用打标记用于判断每个点是否被走过,因为每个数 $x$ 的约数之和 $y$ 是唯一的,建图的时候只从 $y$ 向 $x$ 连边,所以每个结点的父节点是唯一的,所以每个点只会被遍历一次,不会被重复遍历的。
求每个数的约数之和可以用筛法,加边的时候注意循环从 $2$ 开始,因为小于 $2$ 的数在本题中是没有约数之和的。
时间复杂度:$\mathcal{O}(n)$
树的遍历的时间复杂度为 $\mathcal{O}(n)$,筛法求约数之和的时间复杂度为 $\mathcal{O}(n \times \ln n)$,所以总的时间复杂度为 $\mathcal{O}(n)$。
$\texttt{C++}$ 代码:
const int N = 5e4 + 10;
int n, res, s[N], h[N], e[N], ne[N], idx;
// 算树的最长直径
int dfs(int u)
{
int d1 = 0, d2 = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
int d = dfs(j) + 1;
if (d >= d1) d2 = d1, d1 = d;
else if (d >= d2) d2 = d;
}
res = max(res, d1 + d2);
return d1;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
// 计算约数之和
for (int i = 1; i <= n; i ++ )
for (int j = 2; j <= n / i; j ++ )
s[i * j] += i;
for (int i = 2; i <= n; i ++ )
if (i > s[i]) add(s[i], i);
for (int i = 1; i <= n; i ++ ) dfs(i);
cout << res << endl;
return 0;
}