树与图的深度优先搜索
贡献者: 有机物
本文将介绍树与图的深度优先搜索。
树与图的存储:
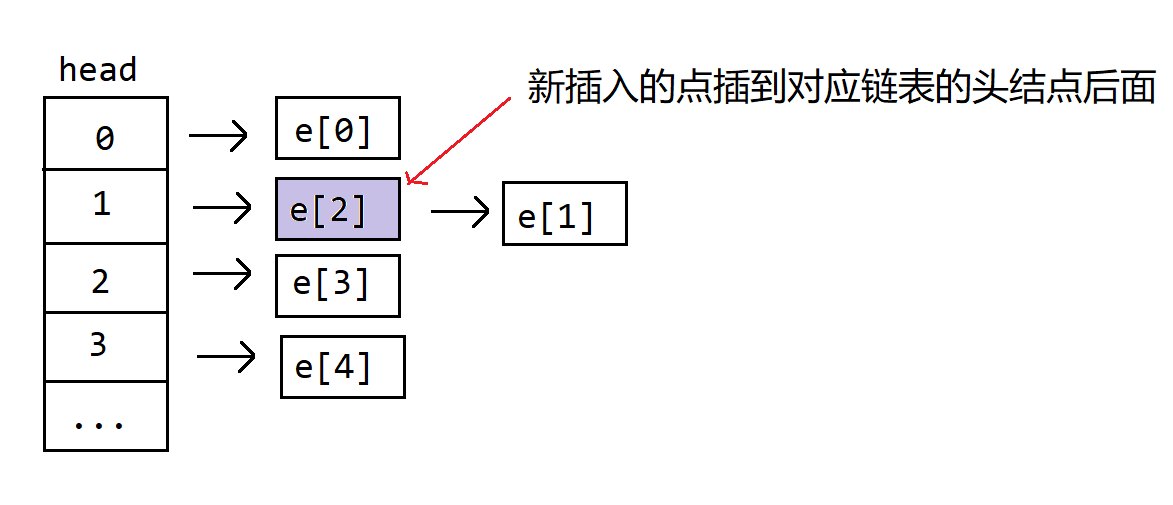
存储可以使用邻接表,邻接表的实现可以使用前面学的单链表,邻接表就是 $n$ 个单链表,邻接表的所使用的数组需要多开一个 head 数组,表示每个单链表的表头。邻接表的插入一般都是头插法,即从单链表的表头插入新结点。
图 1:邻接表插入一个数
可见,对于一张 $n$ 个点 $m$ 条边的图,可以用 $n$ 个单链表构成,$\forall x\in \text{Graph}$ 要想找到 $x$ 的所有出边,可以依据 $x$ 的表头依次访问。
int h[N], e[N], ne[N], idx = 0;
// 在表头是 a 的链表的头结点后面插入一个数 b
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
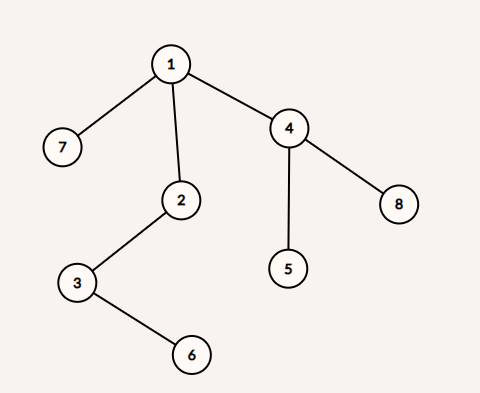
图 2:示例图
const int N = 1e5 + 10, M = N;
int h[N], e[M], ne[M], idx;
void add(int a, int b) // 添加一条边 a->b
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int main()
{
int n; // 结点数
cin >> n;
memset(h, -1, sizeof h); // 初始化每个单链表的表头
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
cin >> a >> b;
// 添加一条无向边 a -- b,等于添加两条有向边 a --> b, b --> a
add(a, b), add(b, a); // 建立双向边(无向边)
}
// 打印邻接表
for (int i = 1; i <= n - 1; i ++ ) // n - 1 条边
{
cout << i << ':';
for (int j = h[i]; j != -1; j = ne[j])
cout << "->" << e[j]; // j 为下标,e[j] 就是值
cout << endl;
}
return 0;
}
/*
输入:
8
1 4
1 2
1 7
4 8
4 5
2 3
3 6
输出:
1:->7->2->4
2:->3->1
3:->6->2
4:->5->8->1
5:->4
6:->3
7:->1
*/
输出的结果就是每个链表的结点的值。
图的深度优先遍历就是从根结点开始选择一条边遍历,遍历到当前边的叶结点就回溯,再继续走到别的分支。
void dfs(int x)
{
st[x] = true;
for (int i = h[x]; ~i; i = ne[i])
{
int j = e[i]; // j 为图中点的编号
if (!st[j]) dfs(j); // 没被访问过就继续遍历
}
}
树的 DFS 序就是每一个结点在深度优先遍历中进出栈的时间序列,最后序列的长度为 $2n$。树的 DFS 序的特点是,对于一个结点 $x$,在序列中会出现两次,那么以这个结点出现的首次和末次的序列就是以这个结点为根的 DFS 序。
void dfs(int x)
{
a[cnt ++ ] = x;
st[x] = true; // 标记 x 结点已经被访问
for (int i = h[x]; ~i; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs(j); // 没被访问过就继续遍历
}
a[cnt ++ ] = x;
}
dfs(1); // 调用入口
// 输出 DFS 序
for (int i = 0; i < cnt; i ++ ) cout << a[i] << ' ';