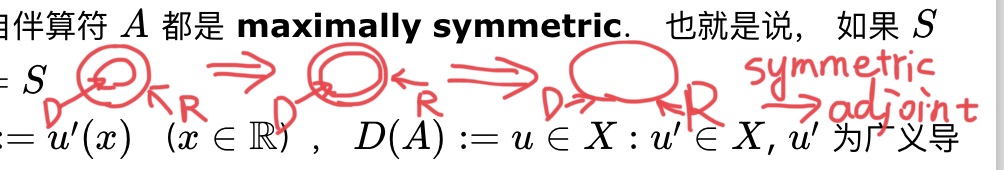伴随算符
贡献者: addis
- 本文处于草稿阶段。
若一个线性算符对应的矩阵是厄米矩阵,那么它就是一个
有限维的线性算符可以表示为
无限维的情况下,和对称算符有什么区别?注意是定义域必须是希尔伯特空间的稠密子空间。
\begin{equation}
\left\langle Au \middle| v \right\rangle = \left\langle u \middle| A ^\dagger v \right\rangle ~
\end{equation}
symmetric 和 adjoint:一个定义域变大,另一个变小,等两个相等时就 adjoint 了
图 1:草图