张量积（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学中，两个向量空间 \( V \) 和 \( W \)（在相同的域上）的张量积 \( V \otimes W \) 是一个向量空间，它与一个双线性映射 \(V \times W \to V \otimes W\) 相关联，该映射将一对 \( (v, w) \)，其中 \( v \in V\), \( w \in W \)，映射到 \( V \otimes W \) 中的一个元素，表示为 \( v \otimes w \)。

　　 形式为 \( v \otimes w \) 的元素称为 \( v \) 和 \( w \) 的张量积。\( V \otimes W \) 中的元素称为张量，两个向量的张量积有时被称为**初等张量**或**可分解张量**。初等张量生成了 \( V \otimes W \)，即 \( V \otimes W \) 中的每个元素都是初等张量的和。如果给定 \( V \) 和 \( W \) 的基，则 \( V \otimes W \) 的基是所有 \( V \) 的基元素与 \( W \) 的基元素的张量积。

　　 两个向量空间的张量积捕捉了所有双线性映射的性质，具体而言，来自 \( V \times W \) 到另一个向量空间 \( Z \) 的双线性映射可以通过线性映射 \(V \otimes W \to Z\) 唯一地分解（见下文标题为 “普遍性质” 的部分），即该双线性映射与从张量积 \( V \otimes W \) 到 \( Z \) 的唯一线性映射相关联。

　　 张量积在许多应用领域中都有使用，包括物理学和工程学。例如，在广义相对论中，重力场通过度量张量来描述，度量张量是一个张量场，每个空间时间流形的点上都有一个张量，并且每个张量属于该点的余切空间与自身的张量积。

1. 定义与构造

　　 两个向量空间的张量积是一个向量空间，它的定义是直到同构的。定义它有几种等价的方式。大多数方式都是显式地定义一个向量空间，称为张量积，通常，这些定义的等价性证明几乎是直接由所定义的向量空间的基本性质得出的。

　　 张量积也可以通过普遍性质来定义；见下文的 “普遍性质” 部分。与所有的普遍性质一样，所有满足该性质的对象通过一个唯一的同构进行同构，并且这个同构与普遍性质兼容。当使用这种定义时，其他定义可以看作是满足普遍性质的对象的构造，并且证明存在满足普遍性质的对象，即证明张量积的存在。

从基底出发

　　 设 \( V \) 和 \( W \) 是定义在域 \( F \) 上的两个向量空间，分别具有基底 \( B_V \) 和 \( B_W \)。

　　 向量空间 \( V \) 和 \( W \) 的张量积 \( V \otimes W \) 是一个向量空间，其基底是所有形式为 \( v \otimes w \) 的集合，其中 \( v \in B_V \) 且 \( w \in B_W \)。这个定义可以通过以下方式进行形式化（这个形式化通常在实践中不常用，因为前述的非正式定义通常已经足够）： \( V \otimes W \) 是从笛卡尔积 \( B_V \times B_W \) 到 \( F \) 的所有函数的集合，这些函数有有限个非零值。通过逐点操作，使得 \( V \otimes W \) 成为一个向量空间。将 \( (v, w) \) 映射为 1，其他 \( B_V \times B_W \) 中的元素映射为 0 的函数表示为 \( v \otimes w \)。

　　 集合 \(\{v \otimes w \mid v \in B_V, w \in B_W\}\) 然后直接构成了 \( V \otimes W \) 的基底，这个基底被称为基底 \( B_V \) 和 \( B_W \) 张量积。

　　 我们可以等价地定义 \( V \otimes W \) 为 \( V \times W \) 上的双线性形式的集合，这些双线性形式在 \( B_V \times B_W \) 的有限个元素上是非零的。为了证明这一点，给定 \( (x, y) \in V \times W \) 和一个双线性形式 \( B: V \times W \to F \)，我们可以将 \( x \) 和 \( y \) 在基底 \( B_V \) 和 \( B_W \) 上分解为： \[ x = \sum_{v \in B_V} x_v v \quad \text{和} \quad y = \sum_{w \in B_W} y_w w~ \] 其中，只有有限个 \( x_v \) 和 \( y_w \) 是非零的，利用 \( B \) 的双线性特性，我们得到： \[ B(x, y) = \sum_{v \in B_V} \sum_{w \in B_W} x_v y_w B(v, w)~ \] 因此，我们看到，对于任何 \( (x, y) \in V \times W \)，\( B \) 的值是唯一且完全由它在 \( B_V \times B_W \) 上的取值决定的。这使我们能够将之前在 \( B_V \times B_W \) 上定义的映射 \( v \otimes w \) 扩展为双线性映射 \( v \otimes w: V \times W \to F \)，通过定义： \[ (v \otimes w)(x, y) := \sum_{v' \in B_V} \sum_{w' \in B_W} x_{v'} y_{w'} (v \otimes w)(v', w') = x_v y_w~ \] 然后，我们可以将任何双线性形式 \( B \) 表示为（可能是无限的）形式线性组合，基于 \( v \otimes w \) 映射，如下所示： \[ B = \sum_{v \in B_V} \sum_{w \in B_W} B(v, w) (v \otimes w)~ \] 使得这些映射类似于向量空间 \( \text{Hom}(V, W; F) \) 的 Schauder 基底，其中 \( \text{Hom}(V, W; F) \) 是所有双线性形式的集合，定义在 \( V \times W \) 上。如果要使其成为一个合适的 Hamel 基底，则只需要添加要求 \( B \) 在 \( B_V \times B_W \) 的有限个元素上非零，并考虑这些映射的子空间。

　　 在任何一种构造中，两个向量的张量积是从它们在基底上的分解定义的。更精确地说，取 \( x \in V \) 和 \( y \in W \) 的基底分解，如前所述： \[ \begin{aligned} x \otimes y &= \left( \sum_{v \in B_V} x_v v \right) \otimes \left( \sum_{w \in B_W} y_w w \right) \\ &= \sum_{v \in B_V} \sum_{w \in B_W} x_v y_w v \otimes w \end{aligned}~ \] 这个定义显然是从 \( B(v, w) \) 在 \( B(x, y) \) 双线性展开中的系数中推导出来的，使用了基底 \( B_V \) 和 \( B_W \)，正如上面所做的那样。然后，可以很容易地验证，通过这个定义，映射 \(\otimes : (x, y) \mapsto x \otimes y\) 是从 \( V \times W \) 到 \( V \otimes W \) 的双线性映射，满足张量积的普遍性质，即任何张量积的构造都满足该性质（见下文）。

　　 如果将其排列成一个矩形阵列，\( x \otimes y \) 的坐标向量就是 \( x \) 和 \( y \) 的坐标向量的外积。因此，张量积是外积的一种推广，即它是超越坐标向量的抽象。

　　 这个张量积定义的一个局限性是，如果改变基底，定义的张量积会不同。然而，在一个基底上分解另一个基底的元素定义了两个向量空间的张量积之间的典范同构，这使得它们可以被识别。此外，与以下两种替代定义相反，这个定义不能扩展为环上模的张量积的定义。

作为商空间

　　 可以通过以下方式构造一个与基底无关的张量积。

　　 设 \( V \) 和 \( W \) 是定义在域 \( F \) 上的两个向量空间。

　　 首先考虑一个向量空间 \( L \)，它的基底是笛卡尔积 \( V \times W \)。也就是说，\( L \) 的基底元素是形如 \( (v, w) \) 的对，其中 \( v \in V \) 和 \( w \in W \)。为了得到这样的向量空间，可以将其定义为从 \( V \times W \to F \) 的函数的向量空间，这些函数有有限个非零值，并将 \( (v, w) \) 与在 \( (v, w) \) 上取值为 1、其他地方取值为 0 的函数等同。

　　 设 \( R \) 是 \( L \) 的一个线性子空间，它由张量积必须满足的关系所生成。更精确地说，\( R \) 由以下形式的元素所生成： \[ \begin{aligned} (v_1 + v_2, w) &- (v_1, w) - (v_2, w), \\ (v, w_1 + w_2) &- (v, w_1) - (v, w_2), \\ (sv, w) &- s(v, w), \\ (v, sw) &- s(v, w), \end{aligned}~ \] 其中 \( v, v_1, v_2 \in V \)，\( w, w_1, w_2 \in W \)，且 \( s \in F \)。

　　 然后，张量积定义为商空间： \[ V \otimes W = L / R~ \] 在这个商空间中，\( (v, w) \) 的像表示为 \( v \otimes w \)。

　　 可以直接证明，这种构造的结果满足下文讨论的普遍性质。（一个非常类似的构造也可以用来定义模的张量积。）

普遍性质

图
图 1：张量积的普遍性质：如果 \( h \) 是双线性的，则存在一个唯一的线性映射 \( \tilde{h} \)，使得图形是可交换的（即，\( h = \tilde{h} \circ \phi \)）。

　　 在本节中，将描述张量积满足的普遍性质。与所有普遍性质一样，满足该性质的两个对象通过一个唯一的同构相互关联。因此，这是一种（非构造性的）定义两个向量空间张量积的方法。在这种背景下，前面定义的张量积构造可以看作是已定义张量积存在性的证明。

　　 这种方法的一个结果是，张量积的每个性质都可以从普遍性质中推导出来，实际上，人们可以忽略用于证明其存在性的具体方法。

　　 张量积的 “普遍性质定义” 如下（回想一下，双线性映射是一个在其每个参数上分别线性的函数）：

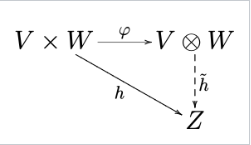
　　 两个向量空间 \( V \) 和 \( W \) 的张量积是一个向量空间，记作 \( V \otimes W \)，以及一个双线性映射 \(\otimes : (v, w) \mapsto v \otimes w\) 从 \( V \times W \) 到 \( V \otimes W \)，使得，对于每一个双线性映射 \( h: V \times W \to Z \)，存在一个唯一的线性映射 \( \tilde{h}: V \otimes W \to Z \)，使得 \(h = \tilde{h} \circ \otimes\)（即，对于每个 \( v \in V \) 和 \( w \in W \)，有 \( h(v, w) = \tilde{h}(v \otimes w) \)）。

线性不相交

　　 像上面的普遍性质一样，以下的表述也可以用来判断给定的向量空间和给定的双线性映射是否构成张量积。\(^\text{[1]}\)

　　 定理 — 设 \( X \)、\( Y \) 和 \( Z \) 为复向量空间，且 \( T: X \times Y \to Z \) 是一个双线性映射。则 \( (Z, T) \) 是 \( X \) 和 \( Y \) 的张量积，当且仅当 \(^\text{[1]}\)\( T \) 的像生成整个 \( Z \)（即，\( \text{span} \ T(X \times Y) = Z \)），并且 \( X \) 和 \( Y \) 是 \( T \)-线性不相交的，定义上是指对于所有正整数 \( n \) 和所有元素 \( x_1, \dots, x_n \in X \) 和 \( y_1, \dots, y_n \in Y \)，如果 \(\sum_{i=1}^{n} T(x_i, y_i) = 0\), 则

  1. 如果所有 \( x_1, \dots, x_n \) 线性无关，则所有 \( y_i \) 都为 0；
  2. 如果所有 \( y_1, \dots, y_n \) 线性无关，则所有 \( x_i \) 都为 0。

　　 等价地，\( X \) 和 \( Y \) 是 \( T \)-线性不相交的，当且仅当对于所有在 \( X \) 中线性无关的序列 \( x_1, \dots, x_m \) 和在 \( Y \) 中线性无关的序列 \( y_1, \dots, y_n \)，向量 \(\{ T(x_i, y_j) : 1 \leq i \leq m, 1 \leq j \leq n \}\) 是线性无关的。

　　 例如，立即可以得出，如果 \( X = \mathbb{C}^m \) 和 \( Y = \mathbb{C}^n \)，其中 \( m \) 和 \( n \) 是正整数，则可以设置 \( Z = \mathbb{C}^{mn} \)，并定义双线性映射为： \[ \begin{aligned} T: \mathbb{C}^m \times \mathbb{C}^n &\to \mathbb{C}^{mn}\\ (x, y) = \left( (x_1, \ldots, x_m), (y_1, \ldots, y_n) \right) &\mapsto (x_i y_j)_{i=1, \ldots, m, j=1, \ldots, n} \end{aligned}~ \] 从而形成 \( X \) 和 \( Y \) 的张量积。\(^\text{[2]}\) 通常，这个映射 \( T \) 被表示为 \( \otimes \)，因此有：\(x \otimes y = T(x, y)\)

　　 作为另一个例子，假设 \( \mathbb{C}^S \) 是定义在集合 \( S \) 上的所有复值函数的向量空间，集合 \( S \) 上的加法和标量乘法按点定义（意味着 \( f + g \) 是映射 \( s \mapsto f(s) + g(s) \) 和 \( c f \) 是映射 \( s \mapsto c f(s) \)）。设 \( S \) 和 \( T \) 是任意集合，对于任何 \( f \in \mathbb{C}^S \) 和 \( g \in \mathbb{C}^T \)，让 \( f \otimes g \in \mathbb{C}^{S \times T} \) 表示由 \( (s, t) \mapsto f(s) g(t) \) 定义的函数。如果 \( X \subseteq \mathbb{C}^S \) 和 \( Y \subseteq \mathbb{C}^T \) 是向量子空间，则向量子空间 \( Z := \text{span} \{ f \otimes g : f \in X, g \in Y \} \) 与双线性映射一起： \[ \begin{aligned} X \times Y &\to Z \\ (f, g) &\mapsto f \otimes g \end{aligned}~ \] 构成 \( X \) 和 \( Y \) 的张量积。\(^\text{[2]}\)

2. 性质

维度

　　 如果 \( V \) 和 \( W \) 是有限维向量空间，那么 \( V \otimes W \) 也是有限维的，且其维度是 \( V \) 和 \( W \) 维度的乘积。

　　 这是因为 \( V \otimes W \) 的基底是通过取 \( V \) 的基底元素与 \( W \) 的基底元素的所有张量积来构成的。

结合性

　　 张量积是结合的，意味着给定三个向量空间 \( U \)、\( V \)、\( W \)，存在一个典范同构： \[ (U \otimes V) \otimes W \cong U \otimes (V \otimes W)~ \] 该同构将 \( (u \otimes v) \otimes w \) 映射到 \( u \otimes (v \otimes w) \)。

　　 这使得在多个向量空间或向量的张量积中可以省略括号。

作为向量空间运算的交换性

　　 两个向量空间 \( V \) 和 \( W \) 的张量积是交换的，意味着存在一个典范同构： \[ V \otimes W \cong W \otimes V~ \] 该同构将 \( v \otimes w \) 映射到 \( w \otimes v \)。

　　 另一方面，即使 \( V = W \)，向量的张量积也不是交换的；即，一般情况下 \( v \otimes w \neq w \otimes v \)。

　　 从 \( V \otimes V \) 到自身的映射 \( x \otimes y \mapsto y \otimes x \) 引入了一个线性自同构，称为编织映射braiding map。更一般地，照常（见张量代数），设 \( V^{\otimes n} \) 表示 \( V \) 的 \( n \) 个副本的张量积。对于前 \( n \) 个正整数的每一个置换 \( s \)，映射： \[ x_1 \otimes \cdots \otimes x_n \mapsto x_{s(1)} \otimes \cdots \otimes x_{s(n)}~ \] 引入了一个从 \( V^{\otimes n} \) 到 \( V^{\otimes n} \) 的线性自同构，这个映射被称为编织映射。

3. 线性映射的张量积

　　 “线性映射的张量积” 重定向至此。有关模的推广，请参见模块的张量积 § 线性映射的张量积和基环的变化。

　　 给定一个线性映射 \( f: U \to V \) 和一个向量空间 \( W \)，其张量积定义为： \[ f \otimes W: U \otimes W \to V \otimes W~ \] 这是唯一的线性映射，满足： \[ (f \otimes W)(u \otimes w) = f(u) \otimes w~ \] 张量积 \( W \otimes f \) 也类似定义。

　　 给定两个线性映射 \( f: U \to V \) 和 \( g: W \to Z \)，它们的张量积定义为： \[ f \otimes g: U \otimes W \to V \otimes Z~ \] 这是唯一的线性映射，满足： \[ (f \otimes g)(u \otimes w) = f(u) \otimes g(w)~ \] 有： \[ f \otimes g = (f \otimes Z) \circ (U \otimes g) = (V \otimes g) \circ (f \otimes W)~ \] 从范畴理论的角度来看，这意味着张量积是一个从向量空间范畴到自身的双变量函子。\(^\text{[3]}\)

　　 如果 \( f \) 和 \( g \) 都是单射或满射，那么上述定义的所有线性映射也都具有相同的性质。特别地，和向量空间的张量积是一个精确函子；这意味着每个精确序列都被映射为一个精确序列（模的张量积不会将单射转换为单射，但它们是右精确函子）。

　　 通过选择所有参与的向量空间的基，线性映射 \( f \) 和 \( g \) 可以通过矩阵表示。然后，取决于张量 \( v \otimes w \) 如何向量化，描述张量积 \( f \otimes g \) 的矩阵是这两个矩阵的克罗内克积。例如，如果上面提到的 \( V \)、\( X \)、\( W \) 和 \( U \) 都是二维的，并且已为它们所有的基定好，那么 \( f \) 和 \( g \) 可以通过以下矩阵表示： \[ A = \begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{bmatrix}, \quad B = \begin{bmatrix} b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2} \end{bmatrix}~ \] 则这两个矩阵的张量积为： \[ \begin{bmatrix} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \end{bmatrix} \otimes \begin{bmatrix} b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2} \end{bmatrix} = \begin{bmatrix} a_{1,1}\begin{bmatrix}b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2}\end{bmatrix} & a_{1,2}\begin{bmatrix}b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2}\end{bmatrix} \\ a_{2,1}\begin{bmatrix}b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2}\end{bmatrix} & a_{2,2}\begin{bmatrix}b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2}\end{bmatrix} \end{bmatrix} = \begin{bmatrix} a_{1,1}b_{1,1} & a_{1,1}b_{1,2} & a_{1,2}b_{1,1} & a_{1,2}b_{1,2} \\ a_{1,1}b_{2,1} & a_{1,1}b_{2,2} & a_{1,2}b_{2,1} & a_{1,2}b_{2,2} \\ a_{2,1}b_{1,1} & a_{2,1}b_{1,2} & a_{2,2}b_{1,1} & a_{2,2}b_{1,2} \\ a_{2,1}b_{2,1} & a_{2,1}b_{2,2} & a_{2,2}b_{2,1} & a_{2,2}b_{2,2} \end{bmatrix}.~ \] 结果的秩至多为 4，因此结果的维度为 4。此处的秩表示张量秩，即所需索引的数量（而矩阵秩计算结果数组中的自由度数目）。 \[ \operatorname{Tr} (A \otimes B) = \operatorname{Tr} A \times \operatorname{Tr} B~ \] 双积是两个相同维度向量之间张量积的特例。

4. 广义张量

　　 对于非负整数 \( r \) 和 \( s \)，在向量空间 \( V \) 上的类型 \( (r, s) \) 张量是以下元素的集合： \[ T_s^r(V) = V \otimes \cdots \otimes V \underset{r}{\otimes} V^* \otimes \cdots \otimes V^* \underset{s}{= } V^{\otimes r} \otimes (V^*)^{\otimes s}.~ \] 其中，\( V^* \) 是对偶向量空间（它包含所有从 \( V \) 到基础域 \( K \) 的线性映射）。

　　 有一个乘法映射，称为张量的（张量）积：\(^\text{[4]}\) \[ T_s^r(V) \otimes_K T_{s'}^{r'}(V) \to T_{s+s'}^{r+r'}(V).~ \] 它通过将所有出现的 “因子” \( V \) 组合在一起定义：将 \( v_i \) 表示为 \( V \) 中的元素，将 \( f_i \) 表示为对偶空间中的元素： \[ (v_1 \otimes f_1) \otimes (v_1') = v_1 \otimes v_1' \otimes f_1.~ \] 如果 \( V \) 是有限维的，那么选择 \( V \) 的基和相应的 \( V^* \) 的对偶基，自然地诱导出 \( T_s^r(V) \) 的基（这个基在 Kronecker 积的文章中有描述）。根据这些基，可以计算两个（或多个）张量的（张量）积的分量。例如，如果 \( F \) 和 \( G \) 分别是阶数为 \( m \) 和 \( n \) 的协变张量（即 \( F \in T_m^0 \) 和 \( G \in T_n^0 \)），那么它们的张量积的分量由下式给出：\(^\text{[5]}\) \[ (F \otimes G)_{i_1 i_2 \cdots i_{m+n}} = F_{i_1 i_2 \cdots i_m} G_{i_{m+1} i_{m+2} \cdots i_{m+n}}.~ \] 因此，两个张量的张量积的分量是每个张量的分量的普通乘积。另一个例子：设 \( U \) 是一个类型为 \( (1, 1) \) 的张量，具有分量 \( U_{\beta}^{\alpha} \)，并且设 \( V \) 是一个类型为 \( (1, 0) \) 的张量，具有分量 \( V^{\gamma} \)。则： \[ (U\otimes V)^{\alpha}{\beta}^{\gamma} = = U^{\alpha} {\beta} V^{\gamma}.~ \] 以及： \[ (V \otimes U)^{\mu \nu}_{\sigma} = V^{\mu} U^{\nu}_{\sigma}.~ \] 配备其乘法操作的张量构成一个代数，称为张量代数。

评价映射和张量收缩

　　 对于类型为 \( (1, 1) \) 的张量，有一个典型的评价映射： \[ V \otimes V^* \to K~ \] 通过其对纯张量的作用定义： \[ v \otimes f \mapsto f(v).~ \] 更一般地，对于类型为 \( (r, s) \) 的张量，且 \( r, s > 0 \)，存在一个映射，称为张量收缩： \[ T_s^r(V) \to T_{s-1}^{r-1}(V).~ \] （此映射应用于的 \( V \) 和 \( V^* \) 的副本必须指定。）

　　 另一方面，如果 \( V \) 是有限维的，则存在一个反向的典型映射（称为共同评价映射）： \[ \begin{cases} K \to V \otimes V^* \\ \lambda \mapsto \sum_i \lambda v_i \otimes v_i^* \end{cases}~ \] 其中，\( v_1, \dots, v_n \) 是 \( V \) 的任意基，\( v_i^* \) 是其对偶基。此映射与基的选择无关。\(^\text{[6]}\)

　　 评价和共同评价的相互作用可以用来表征有限维向量空间，而无需引用基。\(^\text{[7]}\)

伴随表示

　　 张量积空间 \( T^r_s(V) \) 可以自然地被视为李代数 \( \mathrm{End}(V) \) 的一个模，借助于对角作用来定义。为了简明，假设 \( r = s = 1 \)，即我们考虑类型为 \((1,1)\) 的张量。则对于每个 \( u \in \mathrm{End}(V) \)，其作用在 \( a \otimes b \) 上为： \[ u(a \otimes b) = u(a) \otimes b - a \otimes u^*(b)~ \] 其中 \( u^* \in \mathrm{End}(V^*) \) 是 \( u \) 的转置（即对偶映射），满足如下自然对偶配对关系： \[ \langle u(a), b \rangle = \langle a, u^*(b) \rangle~ \] 存在一个典范的同构：\(T^1_1(V) \to \mathrm{End}(V)\) 由以下公式给出： \[ (a \otimes b)(x) = \langle x, b \rangle a~ \] 也就是说，\( a \otimes b \) 被看作作用在向量 \( x \) 上的线性映射，其输出是 \( a \) 乘上 \( x \) 与 \( b \) 的对偶配对值。

　　 通过这个同构，\( \mathrm{End}(V) \) 中的每一个 \( u \) 都可以先被看作 \( T^1_1(V) \) 上的自同构，然后进一步被看作 \( \mathrm{End}(V) \) 上的自同构。事实上，这正是 \( \mathrm{End}(V) \) 上的伴随表示，即 \( \mathrm{ad}(u) \)。

5. 将线性映射视为张量

　　 设 \( U \) 和 \( V \) 是定义在同一域 \( K \) 上的有限维向量空间，记 \( U^* \) 为 \( U \) 的对偶空间，\( \mathrm{Hom}(U, V) \) 为从 \( U \) 到 \( V \) 的所有线性映射所构成的 \( K \)-向量空间。则有一个同构关系： \[ U^* \otimes V \cong \mathrm{Hom}(U, V)~ \] 该同构由纯张量 \( f \otimes v \in U^* \otimes V \) 作用于 \( U \) 中元素 \( u \) 所定义： \[ (f \otimes v)(u) = f(u)v~ \] 其 “逆映射” 可以通过一组基 \( \{u_i\} \) 及其对偶基 \( \{u_i^*\} \) 来定义（参考前文的 “评估映射与张量收缩” 部分）： \[ \begin{cases} \mathrm{Hom}(U, V) \to U^* \otimes V \\ F \mapsto \sum_i u_i^* \otimes F(u_i) \end{cases}~ \] 这个结果意味着： \[ \dim(U \otimes V) = \dim(U) \cdot \dim(V)~ \] 这进一步给出了一个重要事实：若 \( \{u_i\} \)、\( \{v_j\} \) 是 \( U \) 和 \( V \) 的基，则 \( \{u_i \otimes v_j\} \) 形成 \( U \otimes V \) 的一组基。

　　 此外，给定三个向量空间 \( U, V, W \)，张量积与线性映射空间之间还存在如下关系： \[ \mathrm{Hom}(U \otimes V, W) \cong \mathrm{Hom}(U, \mathrm{Hom}(V, W))~ \] 这是一个伴随函子的例子：张量积在此处是 Hom 函子的 “左伴随”。

6. 环上模的张量积

　　 两个模 \( A \) 和 \( B \) 在一个交换环 \( R \) 上的张量积定义方式与域上的向量空间张量积完全相同： \[ A \otimes_R B := F(A \times B)/G~ \] 其中 \( F(A \times B) \) 是由 \( A \times B \) 上生成的自由 \( R \)-模，而 \( G \) 是由以下关系生成的 \( R \)-子模。

　　 更一般地，即使环 \( R \) 不是交换的，张量积也依然可以定义。在这种情况下，要求 \( A \) 是一个右 \( R \)-模，而 \( B \) 是一个左 \( R \)-模，此时不再使用向量空间情形下的最后两个关系，而是引入以下关系： \[ (ar, b) \sim (a, rb)~ \] 如果 \( R \) 是非交换的，那么这个张量积不再是一个 \( R \)-模，而仅仅是一个阿贝尔群。

　　 张量积的泛性质在模的情形下同样成立，只是稍作修改：映射 \(\varphi : A \times B \to A \otimes_R B\) 由 \((a, b) \mapsto a \otimes b\) 定义，被称为 “典范的中线性映射（canonical middle linear map）”\(^\text{[8]}\)，它满足以下性质 \(^\text{[9]}\)： \[ \begin{aligned} \varphi(a + a', b) &= \varphi(a, b) + \varphi(a', b) \\ \varphi(a, b + b') &= \varphi(a, b) + \varphi(a, b') \\ \varphi(ar, b) &= \varphi(a, rb) \end{aligned}~ \] 前两个性质说明 \( \varphi \) 是阿贝尔群 \( A \times B \) 上的双线性映射。第三条性质体现了中线性）：右乘 \( r \) 可在 \( A \) 上前乘，也可在 \( B \) 上后乘。对于任意中线性映射 \( \psi : A \times B \to G \)（其中 \( G \) 是某个阿贝尔群），存在唯一的群同态 \( f : A \otimes_R B \to G \) 使得：\(\psi = f \circ \varphi\).这个性质在群同构意义下唯一确定了 \( \varphi \)。详见主条目中的完整论述。

非交换环上的模的张量积

　　 设 \( A \) 是一个右 \( R \)-模，\( B \) 是一个左 \( R \)-模。则它们的张量积 \( A \otimes_R B \) 是一个阿贝尔群，定义如下： \[ A \otimes_R B := F(A \times B) / G~ \] 其中 \( F(A \times B) \) 是在集合 \( A \times B \) 上生成的自由阿贝尔群，而 \( G \) 是由下列关系生成的子群：

　　 对于所有 \( a, a_1, a_2 \in A \)，\( b, b_1, b_2 \in B \)，以及所有 \( r \in R \)，有： \[ \begin{aligned} &(a_1, b) + (a_2, b) - (a_1 + a_2, b), \\ &(a, b_1) + (a, b_2) - (a, b_1 + b_2), \\ &(ar, b) - (a, rb) \end{aligned}~ \] 张量积的泛性质令 \( G \) 是一个阿贝尔群，且存在一个映射 \(q : A \times B \to G\) 满足双线性性，即对任意 \( a_1, a_2 \in A \)，\( b_1, b_2 \in B \)，\( r \in R \)，都有： \[ \begin{aligned} q(a_1 + a_2, b) &= q(a_1, b) + q(a_2, b), \\ q(a, b_1 + b_2) &= q(a, b_1) + q(a, b_2), \\ q(ar, b) &= q(a, rb) \end{aligned}~ \] 则存在唯一的映射 \(\overline{q} : A \otimes_R B \to G\) 使得：\(\overline{q}(a \otimes b) = q(a, b)\) 对所有 \( a \in A \)、\( b \in B \) 成立。

　　 在某些额外条件下，我们可以为 \( A \otimes_R B \) 赋予模结构：

  1. 若 \( A \) 是一个 \( (S, R) \)-双模（即左 \( S \)-模、右 \( R \)-模，且模结构相容），则 \(A \otimes_R B\) 是一个左 \( S \)-模，其左作用定义为：\(s(a \otimes b) := (sa) \otimes b\)。
  2. 若 \( B \) 是一个 \( (R, S) \)-双模，则 \(A \otimes_R B\) 是一个右 \( S \)-模，其右作用定义为：\((a \otimes b)s := a \otimes (bs)\)。
  3. 若 \( A \) 是一个 \( (S, R) \)-双模，\( B \) 是一个 \( (R, T) \)-双模，则 \(A \otimes_R B \) 是一个 \( (S, T) \)-双模，其中左右作用的定义分别如上所述。
  4. 若 \( R \) 是一个交换环，则 \( A \) 与 \( B \) 都自然成为 \( (R, R) \)-双模，且满足 \(ra := ar, \quad br := rb\)。根据第 3 点，可推出：\(A \otimes_R B\) 是一个 \( (R, R) \)-双模。

张量积的计算

　　 对于向量空间，张量积 \( V \otimes W \) 的计算非常直接，因为如前所述，\( V \) 和 \( W \) 的基可以立即确定 \( V \otimes W \) 的一组基。

　　 但对于一般的（交换）环上的模而言，并非每个模都是自由的。例如，模 \( \mathbf{Z}/n\mathbf{Z} \) 就不是自由的阿贝尔群（也即不是自由的 \( \mathbf{Z} \)-模）。与 \( \mathbf{Z}/n\mathbf{Z} \) 的张量积为： \[ M \otimes_{\mathbf{Z}} \mathbf{Z}/n\mathbf{Z} = M / nM~ \] 更一般地，设 \( M \) 是某个 \( R \)-模，且给定其一个表示，即一组生成元 \( m_i \in M,\, i \in I \) 和一组关系： \[ \sum_{j \in J} a_{ji} m_i = 0,\quad a_{ij} \in R~ \] 则张量积可以通过以下余核来计算： \[ M \otimes_R N = \operatorname{coker}(N^J \to N^I)~ \] 其中 \( N^J = \bigoplus_{j \in J} N \)，\( N^I = \bigoplus_{i \in I} N \)，映射 \( N^J \to N^I \) 的定义为：将第 \( j \) 个拷贝中的某个 \( n \in N \) 发送到 \( a_{ij} n \)（作为 \( N^I \) 中第 \( i \) 个分量）。通俗来说，可以理解为 \( M \) 的一个表示给出了 \( M \otimes_R N \) 的一个表示。这一计算方式反映出张量积是一个右正合函子。但张量积一般不是左正合的，也就是说，对于一个 \( R \)-模的单射：\(M_1 \to M_2\) 张量积下的映射： \[ M_1 \otimes_R N \to M_2 \otimes_R N~ \] 通常不再是单射。

　　 例如，对映射 \( \mathbf{Z} \xrightarrow{n} \mathbf{Z} \)（乘以 \( n \)）施加张量 \( \otimes_{\mathbb{Z}} \mathbf{Z}/n\mathbf{Z} \)，得到的是零映射：\(0 : \mathbf{Z}/n\mathbf{Z} \to \mathbf{Z}/n\mathbf{Z}\) 这显然不是单射。这种张量积不具左正合性的 “缺失” 由所谓的 Tor 上推子函子来度量。所有高阶的 Tor 函子可以组合成所谓的导出张量积。

7. 代数的张量积

　　 设 \( R \) 是一个交换环。如果 \( A \) 和 \( B \) 是 \( R \)-代数，则可以应用张量积的概念。在这种情况下，张量积 \( A \otimes_R B \) 本身是一个 \( R \)-代数，其乘法规则定义为： \[ (a_1 \otimes b_1) \cdot (a_2 \otimes b_2) = (a_1 \cdot a_2) \otimes (b_1 \cdot b_2)~ \] 例如： \[ R[x] \otimes_R R[y] \cong R[x, y]~ \] 一个具体的例子是，当 \(A\) 和 \(B\) 是包含公共子域 \(R\) 的域时，域的张量积与伽罗瓦理论密切相关：假设 \(A = R[x]/f(x)\)，其中 \(f\) 是一个具有 \(R\) 中系数的不可约多项式，那么张量积可以计算为： \[ A \otimes_R B \cong B[x] / f(x)~ \] 在这里，\(f\) 现在被解释为相同的多项式，但其系数被看作 \(B\) 中的元素。在更大的域 \(B\) 中，该多项式可能变得可约，这引入了伽罗瓦理论。例如，如果 \(A = B\) 是 \(R\) 的一个伽罗瓦扩展，则： \[ A \otimes_R A \cong A[x] / f(x)~ \] 作为 A-代数同构于 \(A^{\operatorname{deg}(f)}\)。

8. 张量的特征配置

　　 方阵 \( A \) 的元素位于域 \( K \) 中，表示从向量空间 \( K^n \) 到 \( K^n \) 的线性映射，因此也表示从 \( K \) 上的射影空间 \( \mathbb{P}^{n-1} \) 到 \( \mathbb{P}^{n-1} \) 的线性映射 \( \psi : \mathbb{P}^{n-1} \to \mathbb{P}^{n-1} \)。如果 \( A \) 是非奇异的，则 \( \psi \) 在整个空间中是良定义的，并且 \( A \) 的特征向量对应于 \( \psi \) 的不动点。\( A \) 的特征配置由 \( \mathbb{P}^{n-1} \) 中的 \( n \) 个点组成，前提是 \( A \) 是一般的且 \( K \) 是代数闭域。非线性映射的不动点是张量的特征向量。

　　 令 \( A = (a_{i_1i_2\cdots i_d}) \) 为一个 \( d \)-维张量，格式为 \( n \times n \times \cdots \times n \)，其中元素(\( a_{i_1i_2\cdots i_d} \))位于特征为零的代数闭域 \( K \) 中。这样的张量 \( A \in (K^n)^{\otimes d}\) 定义了从 \( K^n \) 到 \( K^n \) 和从 \( \mathbb{P}^{n-1} \) 到 \( \mathbb{P}^{n-1} \) 的多项式映射，其坐标为： \[ \psi_i(x_1, \ldots, x_n) = \sum_{j_2=1}^{n} \sum_{j_3=1}^{n} \cdots \sum_{j_d=1}^{n} a_{ij_2j_3\cdots j_d} x_{j_2} x_{j_3} \cdots x_{j_d} \quad \text{对于} \ i = 1, \ldots, n~ \] 因此，\( \psi \) 的每个 \( n \) 个坐标 \( \psi_i \) 是一个关于 \( x = (x_1, \ldots, x_n) \) 的次数为 \( d-1 \) 的齐次多项式。\( A \) 的特征向量是约束条件的解： \[ \text{rank} \begin{pmatrix} x_1 & x_2 & \cdots & x_n \\ \psi_1(\mathbf{x}) & \psi_2(\mathbf{x}) & \cdots & \psi_n(\mathbf{x}) \end{pmatrix} \leq 1~ \] 特征配置由这个矩阵的 \( 2 \times 2 \) 子式的代数簇给出。\(^\text{[10]}\)

9. 张量积的其他例子

拓扑张量积

　　 希尔伯特空间将有限维向量空间推广到任意维度。存在一个类似的运算，也叫做 “张量积”，使得希尔伯特空间成为一个对称单子类别。它本质上是作为上述讨论的代数张量积的度量空间完备构造的。然而，它并不满足定义张量积的普遍性质的显著类比；\(^\text{[11]}\) 该性质的态射必须限制为希尔伯特-施密特算子。\(^\text{[12]}\)

　　 在内积强加不适当的情况下，仍然可以尝试将代数张量积完成，作为拓扑张量积。然而，这样的构造不再是唯一确定的：在许多情况下，代数张量积上存在多种自然拓扑。

有序向量空间的张量积

　　 一些向量空间可以分解为子空间的直和。在这种情况下，两个空间的张量积可以分解为子空间乘积的和（类似于乘法对加法的分配）。

表示的张量积

　　 赋予额外乘法结构的向量空间称为代数。这种代数的张量积由小伍德–理查森规则描述。

二次型的张量积

　　 主条目：二次型的张量积

多线性型的张量积

　　 给定两个多线性型 \( f(x_1, \dots, x_k) \) 和 \( g(x_1, \dots, x_m) \)，它们作用在一个向量空间 \( V \) 上，且该向量空间定义在域 \( K \) 上，它们的张量积是多线性型： \[ (f \otimes g)(x_1, \dots, x_{k+m}) = f(x_1, \dots, x_k) g(x_{k+1}, \dots, x_{k+m}).~ \] 这是张量积的特例，如果它们被看作多线性映射（另见张量作为多线性映射）。因此，多线性型张量积的分量可以通过克罗内克积来计算。

张量积的域

　　 主条目：张量积的域

图的张量积

　　 需要提到的是，尽管称为 “张量积”，但这并不是上述意义上的图的张量积；实际上，它是图和图同态范畴中的范畴论产品。然而，它实际上是图的邻接矩阵的克罗内克尔张量积。另请参阅上文中关于线性映射的张量积部分。

单模范畴

　　 张量积的最一般设置是单模范畴。它捕捉了张量的代数本质，而不特定提及被张量化的对象。因此，所有的张量积都可以表达为将单模范畴应用于某个特定设置，作用于某些特定对象。

10. 商代数

　　 可以作为商构造张量代数的多个重要子空间：包括外代数、对称代数、克利福德代数、维尔代数以及一般的普适包络代数。

　　 外代数是通过外积构造的。给定一个向量空间 \( V \)，外积 \( V \wedge V \) 定义为： \[ V \wedge V := V \otimes V / \{ v \otimes v \mid v \in V \}.~ \] 当 \( V \) 的基础域不具有特征 2 时，这一定义等价于： \[ V \wedge V := V \otimes V / \{ v_1 \otimes v_2 + v_2 \otimes v_1 \mid (v_1, v_2) \in V^2 \}.~ \] 外积中，\( v_1 \otimes v_2 \) 的像通常表示为 \( v_1 \wedge v_2 \)，并且由构造可知，满足： \[ v_1 \wedge v_2 = -v_2 \wedge v_1.~ \] 类似的构造可以应用于 \( V \otimes \dots \otimes V \)（\(n\) 个因子），得到 \( \Lambda^n V \)，即 \( V \) 的第 \(n\) 外幂。后者的概念是微分 \(n\)-形式的基础。

　　 对称代数是通过对称积以类似的方式构造的： \[ V \odot V := V \otimes V / \{ v_1 \otimes v_2 - v_2 \otimes v_1 \mid (v_1, v_2) \in V^2 \}.~ \] 更一般地： \[ \operatorname{Sym}^n V := \underbrace{V \otimes \dots \otimes V}_n / (\dots \otimes v_i \otimes v_{i+1} \otimes \dots - \dots \otimes v_{i+1} \otimes v_i \otimes \dots)~ \] 也就是说，在对称代数中，两个相邻的向量（因此所有向量）可以交换。得到的对象被称为对称张量。

11. 编程中的张量积

数组编程语言

　　 数组编程语言可能已经内置了这种模式。例如，在 APL 中，张量积表示为 ○.×（例如 A ○.× B 或 A ○.× B ○.× C）。在 J 中，张量积是 */ 的双目形式（例如 a */ b 或 a */ b */ c）。

　　 J 的处理方式还允许表示某些张量场，因为 a 和 b 可以是函数而非常量。两个函数的这种积是一个派生函数，如果 a 和 b 是可微的，那么 a */ b 也是可微的。

　　 然而，这些类型的符号在数组语言中并不普遍存在。其他数组语言可能需要显式处理索引（例如 MATLAB），并且/或者可能不支持高阶函数，如雅可比导数（例如 Fortran/APL）。

12. 另见

13. 注释

  1. Trèves 2006, 第 403–404 页。
  2. Trèves 2006, 第 407 页。
  3. Hazewinkel, Michiel; Gubareni, Nadezhda Mikhaĭlovna; Gubareni, Nadiya; Kirichenko, Vladimir V. (2004). *Algebras, Rings and Modules*。Springer，第 100 页。ISBN 978-1-4020-2690-4。
  4. Bourbaki (1989)，第 244 页定义了 “张量积 x 和 y” 的用法，它们是各自模块的元素。
  5. 类似的公式也适用于逆变张量以及混合变数的张量。尽管在许多情况下，如定义了内积时，这种区别是无关紧要的。
  6. “向量空间上的共评价”。《无所辩解的数学家》，2008 年 11 月 13 日。原文已归档于 2017 年 2 月 2 日。2017 年 1 月 26 日访问。
  7. 参见紧闭范畴。
  8. Hungerford, Thomas W. (1974). *Algebra*。Springer。ISBN 0-387-90518-9。
  9. Chen, Jungkai Alfred (2004 年春)，"Tensor product"（PDF），《高级代数 II》 (讲义)，国立台湾大学，已归档（PDF）自原文于 2016 年 3 月 4 日。
  10. Abo, H.; Seigal, A.; Sturmfels, B. (2015). "张量的特征配置"。arXiv:1505.05729 [math.AG]。
  11. Garrett, Paul (2010 年 7 月 22 日). "Hilbert 空间的张量积不存在"（PDF）。
  12. Kadison, Richard V.; Ringrose, John R. (1997). *操作代数理论基础*。研究生数学系列。第 I 卷。Providence, R.I.: 美国数学学会。定理 2.6.4。ISBN 978-0-8218-0819-1。MR 1468229。
  13. Tu, L. W. (2010). *流形引论*。Universitext。Springer，第 25 页。ISBN 978-1-4419-7399-3。

14. 参考文献

                     

© 保留一切权利