卷绕数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：这条曲线相对于点 $p$ 的绕数是 2。

　　 在数学中，闭合曲线相对于平面中某一点的绕数或绕线指数是一个整数，表示该曲线绕该点逆时针方向环绕的总次数，也就是曲线的 “转数”。对于某些非闭合的平面曲线，其绕数可能是非整数。绕数依赖于曲线的方向：如果曲线沿顺时针方向绕点运动，则绕数为负数。

　　 绕数是代数拓扑中的基础研究对象，并且在向量分析、复分析、几何拓扑、微分几何以及物理学（例如弦理论）中都扮演着重要角色。

1. 直观描述

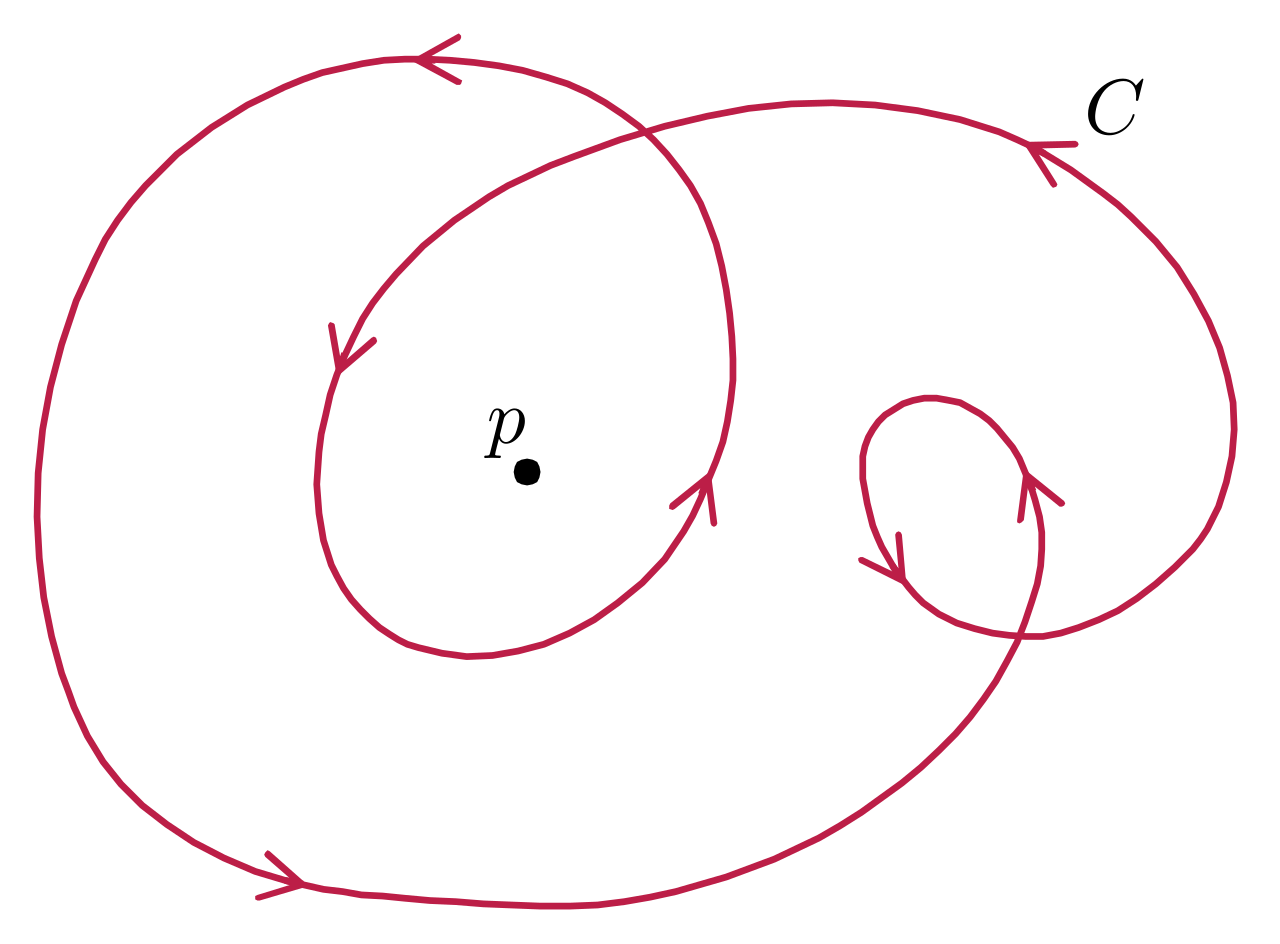
　　 沿着红色曲线运动的一个物体，会绕位于原点的人逆时针转两圈。 假设我们有一条位于 $xy$ 平面上的闭合、有方向的曲线。我们可以把这条曲线想象成某个物体的运动轨迹，而曲线的方向表示物体运动的方向。这样，这条曲线的绕数就等于该物体绕原点逆时针转的总圈数。

　　 在计算总圈数时，逆时针的运动计为正数，而顺时针的运动计为负数。例如，如果一个物体先绕原点逆时针转了四圈，然后又绕原点顺时针转了一圈，那么这条曲线的总绕数就是 3。

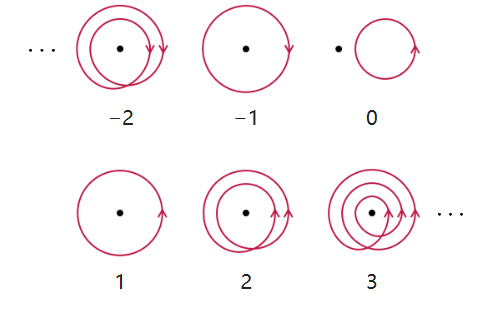
　　 按照这个规则，一条完全没有绕过原点的曲线，其绕数为 0；而一条绕原点顺时针运动的曲线，其绕数为负数。因此，曲线的绕数可以是任意整数。下面的图示展示了绕数从 −2 到 3 的不同曲线。

图
图 2

2. 形式化定义

　　 设 $\gamma: [0,1] \to \mathbb{C} \setminus \{a\}$ 是一条平面上去掉点 $a$ 后的连续闭合路径。曲线 $\gamma$ 绕点 $a$ 的绕数定义为整数： $$ \mathrm{wind}(\gamma, a) = s(1) - s(0),~ $$ 其中 $(\rho, s)$ 是该路径用极坐标表示的形式，即通过如下覆盖映射 $p$ 提升得到的路径： $$ p: \mathbb{R}_{>0} \times \mathbb{R} \to \mathbb{C} \setminus \{a\} : (\rho_0, s_0) \mapsto a + \rho_0 e^{i 2\pi s_0}.~ $$ 绕数的良好定义性源于提升路径的存在性和唯一性（给定覆盖空间的起点），并且因为映射 $p$ 的所有纤维都具有以下形式：$\rho_0 \times (s_0 + \mathbb{Z})$，所以上述表达式不依赖于起点的具体选择。由于路径是闭合的，最终得到的绕数是一个整数。

3. 替代表述

　　 在数学的不同分支中，绕数常常有不同的定义方式。下面列出的所有定义都与前面给出的定义是等价的：

亚历山大编号法

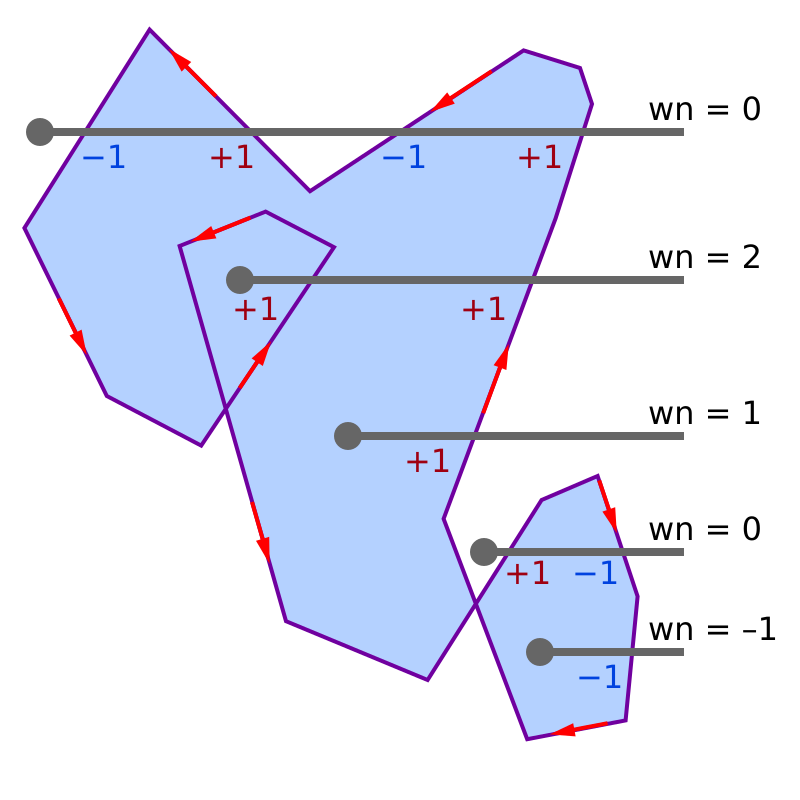
　　 1865 年，奥古斯特·费迪南德·莫比乌斯，首次提出了一种用简单组合规则来定义绕数的方法 \(^\text{[1]}\)；1928 年，小詹姆斯·沃德尔·亚历山大又独立地提出了同样的规则。\(^\text{[2]}\) 根据该方法，任意一条曲线都会将平面分割成若干个连通区域，其中有一个区域是无界的。这一定义具有以下性质：在同一个区域内的任意两点，其对应的绕数是相同的。无界区域内（即平面外延处任意点）的绕数为 0。相邻两个区域的绕数之差正好是 1；其中绕数较大的区域出现在曲线运动方向的左侧。

微分几何

　　 在微分几何中，参数方程通常假定是可微的（或至少是分段可微的）。在这种情况下，极坐标角 $\theta$ 与直角坐标 $x$ 和 $y$ 的关系由以下公式给出： $$ d\theta = \frac{1}{r^{2}}\left(x\,dy - y\,dx\right) \quad\text{其中 } r^{2} = x^{2} + y^{2}.~ $$ 这个公式可以通过对 $\theta$ 的定义进行求导得到： $$ \theta(t) = \arctan\!\left(\frac{y(t)}{x(t)}\right).~ $$ 根据微积分基本定理，$\theta$ 的总变化量等于 $d\theta$ 的积分。因此，一条可微曲线的绕数可以表示为一条曲线积分： $$ \text{wind}(\gamma, 0) = \frac{1}{2\pi} \oint_{\gamma} \left(\frac{x}{r^{2}}\,dy - \frac{y}{r^{2}}\,dx\right).~ $$ 在去掉原点的平面上，微分形式 $d\theta$ 是一个闭合但非全微分的 1-形式，它生成了穿孔平面的第一 de Rham 上同调群。特别地，如果 $\omega$ 是定义在去掉原点的平面上的任意一个闭合的、可微的 1-形式，那么沿任意闭合路径积分 $\omega$ 的结果都会是绕数的某个倍数。

复分析

　　 在复分析中，绕数在许多理论中都起着极其重要的作用（例如留数定理的表述）。在复分析的语境下，复平面上一条闭合曲线 $\gamma$ 的绕数可以用复坐标 $z = x + iy$ 来表示。若写作 $z = r e^{i\theta}$，则有： $$ dz = e^{i\theta}dr + i r e^{i\theta} d\theta~ $$ 因此： $$ \frac{dz}{z} = \frac{dr}{r} + i\,d\theta = d[\ln r] + i\,d\theta.~ $$ 由于 $\gamma$ 是闭合曲线，$ \ln\left(r\right) $ 的总变化量为零，因此积分 $\frac{dz}{z}$ 等于 $i$ 乘以 $\theta$ 的总变化量。由此，曲线 $\gamma$ 绕原点的绕数为 \(^\text{[3]}\)： $$ \frac{1}{2\pi i} \oint_{\gamma} \frac{dz}{z}.~ $$ 更一般地，如果曲线 $\gamma$ 由参数 $t \in [\alpha, \beta]$ 表示，且对于复平面上的某点 $z_0$，有 $z_0 \notin \gamma([\alpha, \beta])$，那么曲线 $\gamma$ 绕点 $z_0$ 的绕数（也称为曲线 $\gamma$ 关于 $z_0$ 的指标）定义为 \(^\text{[4]}\)： $$ \mathrm{Ind}_{\gamma}(z_0) = \frac{1}{2\pi i} \oint_{\gamma} \frac{d\zeta}{\zeta - z_0} = \frac{1}{2\pi i} \int_{\alpha}^{\beta} \frac{\gamma'(t)}{\gamma(t) - z_0}\, dt.~ $$ 这个公式正是著名的柯西积分公式的一个特例。

　　 在复平面中，绕数的一些基本性质可以通过以下定理给出：\(^\text{[5]}\)

　　 定理:设 $\gamma:[\alpha,\beta]\to\mathbb{C}$ 是一条闭合路径，并令 $\Omega := \mathbb{C} \setminus \gamma([\alpha,\beta])$ 表示曲线 $\gamma$ 的像的补集。那么，曲线 $\gamma$ 关于点 $z$ 的指标（即绕数）定义为： $$ \mathrm{Ind}_{\gamma}:\Omega\to\mathbb{C}, \quad z \mapsto \frac{1}{2\pi i} \oint_{\gamma} \frac{d\zeta}{\zeta - z},~ $$ 并且它满足以下性质：1.$\mathrm{Ind}_{\gamma}(z) \in \mathbb{Z}, \quad \forall z\in\Omega$;2. 分区常数性：在 $\Omega$ 的每一个连通分支（即最大连通子集）上，$\mathrm{Ind}_{\gamma}(z)$ 是常数；3. 无界区域的零绕数：若点 $z$ 位于 $\Omega$ 的无界连通区域，则 $\mathrm{Ind}_{\gamma}(z) = 0$.

　　 推论:该定理直接给出了圆形路径绕某点的绕数。如预期一样，绕数等于曲线 $\gamma$ 绕该点逆时针环绕的次数。若路径 $\gamma$ 定义为：$\gamma(t) = a + r e^{int}, \quad 0 \leq t \leq 2\pi, \quad n \in \mathbb{Z},$ 则有： $$ \mathrm{Ind}_{\gamma}(z) = \begin{cases} n, & |z-a|< r;\\[6pt] 0, & |z-a|>r. \end{cases}~ $$

拓扑学

　　 在拓扑学中，绕数是连续映射的度的另一种称呼；在物理学中，绕数则常被称为拓扑量子数。两种情况下，本质上描述的都是同一个概念。

　　 上述曲线绕某点的例子有一个简单的拓扑解释：平面去掉一点后的空间与一个圆 $S^1$ 是同伦等价的，因此从圆到自身的映射是需要重点考虑的对象。可以证明，每一个这样的映射都可以连续变形（同伦）为某个标准映射：$S^1 \;\to\; S^1: \; s \;\mapsto\; s^n$,其中，圆上的乘法是通过将其识别为复平面上的单位圆来定义的。从一个圆映射到某个拓扑空间的所有同伦类组成一个群，这个群被称为该空间的**第一同伦群（fundamental group 或 $\pi_1$）。圆的第一同伦群是整数群 $\mathbb{Z}$，而复平面上一条曲线的绕数，实际上就是它对应的同伦类。

　　 类似地，从三维球面 $S^3$ 到自身的映射也可以用一个整数进行分类，这个整数同样被称为绕数，有时也称为庞特里亚金指数。

4. 转数

图
图 3：这条曲线的总曲率为 $6\pi$，转数为 3，尽管它绕点 $p$ 的绕数只有 2。

　　 人们也可以考虑一条路径相对于自身切向方向的绕数。把路径看作随时间变化的运动轨迹时，这相当于求速度向量相对于原点的绕数。在这种情况下，本篇文章开头的示例中，由于包含了小环路，所以绕数为 3。

　　 这种定义仅适用于浸入路径（即处处可微且导数不为零的路径），其值等于切向高斯映射的度。

　　 这种数值被称为转数、旋转数 \(^\text{[6]}\)、旋转指数 \(^\text{[7]}\) 或曲线指数，并且可以通过总曲率除以 $2\pi$ 来计算。

多边形

　　 在多边形中，转数也被称为多边形密度。对于凸多边形，以及更一般的简单多边形（即不自交的多边形），根据约旦曲线定理，其密度为 1。相比之下，对于一个正星形多边形 $\{p/q\}$，其密度为 $q$。

空间曲线

　　 对于空间曲线，无法直接定义转数，因为 “度” 的概念要求维度匹配。然而，对于局部凸的闭合空间曲线，可以定义一个切向转向符号：$(-1)^d$,其中 $d$ 是其切向指示曲线的立体投影的转数。该符号的两种取值对应于局部凸曲线的两类非退化同伦类。\(^\text{[8][9]}\)

5. 绕数与海森堡铁磁方程

　　 绕数与(2+1)维连续海森堡铁磁方程及其可积扩展方程（如 Ishimori 方程等）密切相关。这些方程的解可以通过绕数或拓扑荷（即拓扑不变量和/或拓扑量子数）进行分类。

6. 应用

多边形内点问题

图
图 4：丹·Sunday 绕数算法的可视化示意图：绕数为 0 表示该点在多边形外部；绕数为其他值则表示该点在多边形内部。

　　 一个点相对于某个多边形的绕数可以用来解决点在多边形内 (Point in Polygon, PIP)问题，也就是判断该点是否位于多边形内部。

　　 通常情况下，射线投射算法更适合解决 PIP 问题，因为与绕数算法不同，它不需要三角函数计算。不过，绕数算法也可以通过优化加速，从而同样避免涉及三角函数的运算 \(^\text{[10]}\)。这种优化版本也被称为 Sunday 算法，特别适用于需要处理非简单多边形的场景。

7. 参见

8. 参考文献

  1. Möbius, August (1865). "Über die Bestimmung des Inhaltes eines Polyëders". *Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften, Mathematisch-Physische Klasse*. 17: 31–68.
  2. Alexander, J. W. (1928 年 4 月). "Topological Invariants of Knots and Links". *Transactions of the American Mathematical Society*. 30 (2): 275–306. doi:10.2307/1989123. JSTOR 1989123.
  3. Weisstein, Eric W. "Contour Winding Number". *MathWorld*. 2022 年 7 月 7 日检索。
  4. Rudin, Walter (1976). *Principles of Mathematical Analysis*. McGraw-Hill. 第 201 页. ISBN 0-07-054235-X.
  5. Rudin, Walter (1987). *Real and Complex Analysis* (第 3 版). McGraw-Hill. 第 203 页. ISBN 0-07-054234-1.
  6. Abelson, Harold (1981). *Turtle Geometry: The Computer as a Medium for Exploring Mathematics*. MIT Press. 第 24 页.
  7. Do Carmo, Manfredo P. (1976). "5. Global Differential Geometry". *Differential Geometry of Curves and Surfaces*. Prentice-Hall. 第 393 页. ISBN 0-13-212589-7.
  8. Feldman, E. A. (1968). "Deformations of closed space curves". *Journal of Differential Geometry*. 2 (1): 67–75. doi:10.4310/jdg/1214501138. S2CID 116999463.
  9. Minarčík, Jiří; Beneš, Michal (2022). "Nondegenerate homotopy and geometric flows". *Homology, Homotopy and Applications*. 24 (2): 255–264. arXiv:1807.01540. doi:10.4310/HHA.2022.v24.n2.a12. S2CID 252274622.
  10. Sunday, Dan (2001). "Inclusion of a Point in a Polygon". 2013 年 1 月 26 日存档。

9. 外部链接

                     

© 保留一切权利