最大期望算法

贡献者： addis

　　（本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

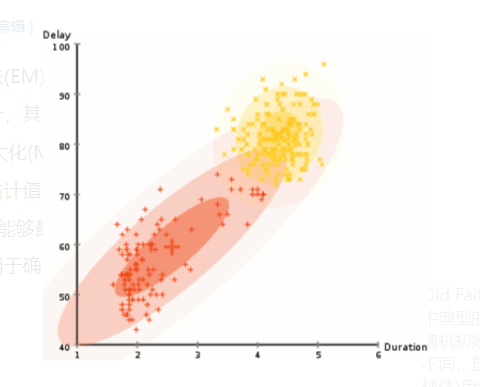
　　在统计学中，期望最大化算法(EM)是一种迭代方法，用于寻找统计模型中参数的最大似然或最大后验估计，其中模型依赖于未观察到的潜变量。EM 迭代在执行求期望(E)步骤和最大化(M)步骤之间交替进行，求期望(E)步骤创建了一个函数，是用参数当前估计值所估计得到的对数似然的期望的函数，最大化(M)步骤计算参数，使其能够最大化在 E 步骤中计算得到的对数似然的期望。然后这些参数估计值被用于确定下一个 E 步骤中的潜变量分布。

图 1：Old Faithful eruption 数据集(R 语言中典型的数据集)上的 EM 聚类过程。随机初始化的模型(由于轴之间的规模不同，显示的是两个非常扁平又宽的球体)用于拟合观测数据。在第一次迭代中，模型的变化非常可观，但之后就在两步之间间歇收敛。由 ELKI 可视化。

1. 历史

　　亚瑟·登普斯特、楠·莱尔德和唐纳德·鲁宾在 1977 年的一篇经典论文中解释了 EM 算法并给出了它的名字。[1]他们指出，这种方法由早期作者 “在特殊情况下提出了很多次”。最早的方法之一是由塞德里克·史密斯提出的用于估计等位基因频率的基因计数法。[2]罗尔夫·桑德伯格在与佩尔·马丁-洛夫和安德斯·马丁·洛夫合作之后，[3][4][5][6][7][8][9]在他的学位论文和其他几篇论文中发表了关于指数族的 EM 方法的非常详细的论述。[10][11][12]登普斯特-莱尔德-鲁宾在 1977 年的论文中推广了这种方法，并对更广泛的一类问题进行了收敛性分析。除开早期的创新发现之外，登普斯特-莱尔德-鲁宾在《皇家统计学会杂志》上发表的具有创新性的论文在皇家统计学会会议上受到热烈讨论，桑德伯格称这篇论文 “非常出色”。登普斯特-莱尔德-鲁宾论文将 EM 方法确立为统计分析的重要工具。

　　登普斯特-莱尔德-鲁宾算法的收敛性分析是有缺陷的，正确的收敛性分析由吴建福于 1983 年发表。[13]吴的证明在指数簇之外建立了 EM 方法的收敛性，正如登普斯特-莱尔德-鲁宾所声称的那样。[13]

2. 介绍

　　 EM 算法用于在方程不能直接求解的情况下找到统计模型的(局部)最大似然参数。典型情况下，这些模型除了未知参数和已知可观测到的数据之外，还涉及潜变量。也就是说，要么数据中存在缺失值，要么可以通过假设存在更多未观察到的数据点来更简单地建立模型。例如，可以通过假设每个观察到的数据点具有相应的未观察到的数据点或潜在变量，指定每个数据点所属的混合成分，来更简单地描述混合模型。

　　寻找最大似然解通常需要对所有未知值、参数和潜变量函数取似然函数的导数，同时求解所得方程。在包含潜变量的统计模型中，这通常是不可能的。相反，结果通常是一组互锁方程，其中参数的解需要知道潜变量的值，反之亦然，如果将一组方程代入另一组方程则会产生不可解方程。

　　 EM 算法是从观察到有一种方法可以用数值方法解决这两组方程开始的。可以简单地为两组未知数中的一组选取任意值，用它们来估计另一组，再用这些新的值来找到第一组更好的估计，然后在两者之间不断交替迭代，直到结果值都收敛到不动点。这是否有效还不清楚，但可以证明，在这种情况下它是有效，并且可能性的导数在该点(任意接近)为零，这意味着该点要么是极大值，要么是鞍点。[13] 一般来说，可能会出现多个极大值，但不能保证会找到全局最大值。某些似然也存在奇点，即无意义的最大值。例如，这样的一个解：在混合模型中，EM 可以找到的方法包括将其中一个分量的方差设置为零，并且将同一分量的平均参数设置为等于其中一个数据点。

3. 描述

　　在生成观测数据集合 $X$ 的统计模型，一组未观察到的潜在数据或缺失值 $Z$，以及似然函数

　　 $L(\theta; X, Z) = p(X, Z | \theta)$ 中的未知参数向量 $\theta$，最大似然估计是通过最大化观测数据的边缘似然来确定的：

　　 $$L(\theta; X) = p(X | \theta) = \int p(X, Z | \theta) dZ~.$$

　　然而，这个量通常是难以处理的（例如，如果 $Z$ 是一个事件序列，那么数值的数量随着序列长度呈指数增长，因求积的精确值将是非常困难的）。

　　 EM 算法通过迭代应用这两个步骤来寻找边缘似然的最大似然估计：

　　求期望步骤：定义 $Q(\theta | \theta^{(t)})$ 对数似然函数的期望值为 $\theta$，就目前的条件分布而言 $Z$ 考虑到 $X$ 和参数的前估计 $\theta^{(t)}$(d ) :

　　 $$Q(\theta | \theta^{(t)}) = E_{Z|X,\theta^{(t)}} [\log L(\theta; X, Z)]~.$$

　　最大化步骤(M 步): 查找最大化此数量的参数：

　　 $$\displaystyle \theta^{(t+1)} = \mathop{\arg \max}_{\theta}\ \ Q(\theta | \theta^{(t)})~.$$

　　应用 EM 的典型模型是将 $Z$ 作为一个潜在变量，表示在一组组中的成员：

观测到的数据点 $X$ 可以是离散的（取有限或无限集合的值）或连续的（取或不可数无限集合的值）。与每个数据点相关联的可以是观察是否。
缺失的值(又名潜变量) $Z$ 是离散的，从固定数量的值中提取，每个观察单位有一个潜在变量。
参数是连续的，并且有两种：与所有数据点相关联的参数，以及与潜在变量的特定值相关联的参数(即，与对应潜在变量具有该值的所有数据点相关联的参数

　　然而，也可以将 EM 应用于其他类型的模型。

　　动机如下。如果参数的值 $\theta$ 已知，通常情况下潜变量 $Z$ 的值可以通过最大化所有可能值的对数似然来找到，要么简单地迭代 $Z$ 或者通过隐马尔可夫模型的鲍姆-韦尔奇算法来计算。相反，如果我们知道潜变量 $Z$ 的值，我们要找到参数 $\theta$ 的估计值相当容易，通常通过简单地根据相关联的潜在变量的值对观察到的数据点进行分组，并对每个组中的点的值进行平均或其他的操作。这提出了一种迭代算法，在这两种情况下 $\theta$ 和 $Z$ 未知：

首先，初始化参数 $\theta$ 一些随机值。
在给定 $\theta$ 的情况下，计算每个 $Z$ 可能值的概率。
然后，使用刚刚计算得到的 $Z$ 的值来计算更好的参数估计 $\theta$。
重复步骤 2 和 3，直到收敛。

　　刚刚描述的算法单调地接近成本函数的局部最小值。

4. 性能

　　说到期望 (E) 步骤有点用词不当。第一步的计算是固定的、依赖于数据的参数 $Q$。一旦 $Q$ 的参数已知，在 EM 算法的第二步(M)中，它能被完全确定并被最大化。

　　虽然 EM 迭代确实增加了观测数据(即边缘)的似然函数，但不保证序列收敛到最大似然估计量。对于多模态分布，这意味着 EM 算法可以收敛到观察到的数据似然函数的局部最大值，这取决于起始值。存在各种启发式或元启发式方法来逃离局部最大值，例如随机重启爬山(从几个不同的随机初始估计开始 $\theta^{(t)}$ 或应用模拟退火方法。

　　当似然是指数族时，EM 特别有用：E 步骤成为充分统计量的期望的和，M 步骤则是最大化一个线性函数。在这种情况下，通常可以使用桑德伯格公式(罗尔夫·桑德伯格使用佩尔·马丁-洛夫和安德斯·马丁-洛夫未发表的结果发表)推导出每一步的封闭形式表达式来更新每一步。[11][12][5][6][7][8][9]

　　在登普斯特、莱尔德和鲁宾的原始论文中，EM 方法被修改为计算贝叶斯推断的最大后验估计。

　　还有其他方法可以找到最大似然估计，如梯度下降法、共轭梯度法或高斯-牛顿算法的变体。与 EM 不同，这种方法通常需要评估似然函数的一阶和/或二阶导数。

5. 正确性的证明

　　期望最大化有助于提高 $Q(\theta \mid \theta^{(t)})$ 而不是直接改进

　　 $\log p(\mathbf{X} \mid \theta)$。这里可以证明，对前者的改进意味着对后者的改进。

　　对任意概率 $p(\mathbf{Z} \mid \mathbf{X}, \theta)$ 非零的 $\mathbf{Z}$，我们可以得到 $$\log p(\mathbf{X} \mid \theta) = \log p(\mathbf{X}, \mathbf{Z} \mid \theta) - \log p(\mathbf{Z} \mid \mathbf{X}, \theta)~.$$

　　我们对未知数据 $\mathbf{Z}$ 的可能值在当前参数估计 $\theta^{(t)}$ 下取期望，通过将两边乘以 $p(\mathbf{Z} \mid \mathbf{X}, \theta^{(t)}) $ 并对 $\mathbf{Z}$ 求和（或积分）。左边是一个常数的期望值，所以我们得到：

\begin{align} \log p(\mathbf{X} \mid \boldsymbol{\theta}) &= \sum_{\mathbf{Z}} p(\mathbf{Z} \mid \mathbf{X}, \boldsymbol{\theta}^{(t)}) \log p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol{\theta}) - \sum_{\mathbf{Z}} p(\mathbf{Z} \mid \mathbf{X}, \boldsymbol{\theta}^{(t)}) \log p(\mathbf{Z} \mid \mathbf{X}, \boldsymbol{\theta}) \\ &= Q(\theta \mid \boldsymbol{\theta}^{(t)}) + H(\theta \mid \boldsymbol{\theta}^{(t)}),~ \end{align}

其中 $H(\theta \mid \theta^{(t)})$ 由它所替换那部分求和的负数所定义。最后一个等式对任何值成立，包括 $\theta = \theta^{(t)}$， $$\log p(\mathbf{X} \mid \theta^{(t)}) = Q(\theta^{(t)} \mid \theta^{(t)}) + H(\theta^{(t)} \mid \theta^{(t)})~,$$ 从前面的等式中减去最后一个等式 $$\log p(\mathbf{X} \mid \theta) - \log p(\mathbf{X} \mid \theta^{(t)}) = Q(\theta \mid \theta^{(t)}) - Q(\theta^{(t)} \mid \theta^{(t)}) + H(\theta \mid \theta^{(t)}) - H(\theta^{(t)} \mid \theta^{(t)})~,$$ 然而，吉布斯不等式告诉我们 $H(\theta \mid \theta^{(t)})\geq H(\theta^{(t)} \mid \theta^{(t)})$, 所以我们可以得出结论 $$\log p(\mathbf{X} \mid \theta) \geq Q(\theta \mid \theta^{(t)}) - Q(\theta^{(t)} \mid \theta^{(t)})~.$$ 换句话说，选择 $\theta$ 使得 $\log p(\mathbf{X} \mid \theta)$ 变大的程度至少有 $Q(\theta \mid \theta^{(t)})$ 变大程度这么多。

6. 作为最大化-最大化过程

　　 EM 算法可以看作两个交替的最大化步骤，一个例子是坐标上升。[15][16]考虑以下函数: $$F(q, \theta) := \mathbb{E}_q[\log L(\theta; x, Z)] + H(q)~,$$ 其中 $q$ 是未观测数据 $z$ 的任意概率分布，$H(q)$ 是分布 $q$ 的熵。这个函数可以写为 $$F(q, \theta) = -D_{KL}(q \parallel p_{Z|X}(\cdot \mid x; \theta)) + \log L(\theta; x)~,$$ 其中 $p_{Z|X}(\cdot \mid x; \theta)$ 是给定观测数据情况下，未观测数据 $x$ 的条件分布，$D_{KL}$ 就是信息增益。

　　那么 EM 算法中的步骤可以看作：

　　期望步骤：选择 $q$ 最大化 $F(d)$: $$q^{(t)} = \arg \max_q F(q, \theta^{(t)})~,$$ 最大化步骤：选择 $\theta$ 最大化 $F(d)$: $$\theta^{(t+1)} = \arg \max_\theta F(q^{(t)}, \theta)~.$$

7. 应用

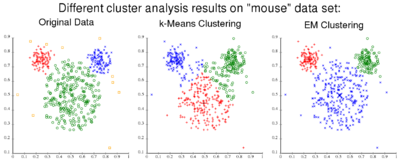
　　 EM 经常用于机器学习和计算机视觉中的数据聚类。在自然语言处理中，该算法的两个突出例子是隐马尔可夫模型的鲍姆-韦尔奇算法和概率上下文无关文法的无监督归纳的内外算法。

　　 EM 经常用于混合模型的参数估计，[17][18]尤其是在数量遗传学方面。[19]

　　在心理测量学中，EM 对于估计项目参数和项目反应理论模型的潜在能力几乎是不可或缺的。

　　凭借处理缺失数据和观察未知变量的能力，新兴市场正成为投资组合定价和风险管理的有用工具。

　　 EM 算法(及其更快的变体有序子集期望最大化)也广泛用于医学图像重建，尤其是正电子发射断层成像和单光子发射计算机断层成像。

　　在结构工程中，使用期望最大化的结构识别[20]算法是一种使用传感器数据识别结构系统固有振动特性的纯输出方法。

8. 滤波和平滑电磁算法

　　卡尔曼滤波器通常用于在线状态估计，最小方差平滑器可以用于离线或批量状态估计。然而，这些最小方差解需要状态空间模型参数的估计。EM 算法可用于解决联合状态和参数估计问题。

　　滤波和平滑 EM 算法通过重复以下两步过程产生:

　　 E 步骤

　　运行卡尔曼滤波器或用当前参数估计值设计的最小方差平滑器，以获得更新的状态估计值。

　　 M 步骤

　　使用最大似然计算中的滤波或平滑状态估计来获得更新的参数估计。假设卡尔曼滤波器或最小方差平滑器对具有附加白噪声的单输入单输出系统的测量值进行操作。可以从最大似然计算中获得更新的测量噪声方差估计

\begin{equation} \hat\sigma_v^2 = \frac{1}{N} \sum_{k=1}^{N} \left( z_k - \hat{x}_k \right)^2~, \end{equation}

其中 $\hat{x}_k$) 标量的输出估计是由滤波器或 $N$ 个标量测量值 $z_k$ 的平滑器计算得到的。上述更新也可以应用于更新自松测量噪声强度。类似地，对于一步自回归过程，更新过的噪声方差估计可以通过下式计算

\begin{equation} \hat\sigma_w^2 = \frac{1}{N} \sum_{k=1}^{N} \left( \hat{x}_{k+1} - \hat{F} \hat{x}_k \right)^2~, \end{equation}

其中 $\hat{x}_k$ 和 $\hat{x}_{k+1}$ 是由滤波器或平滑器计算的标准状态估计。更新的模型参数估计 $\hat{F}$ 通过以下方式获得

\begin{equation} \hat{\mathbf{F}} = \frac{\sum_{k=1}^{N} (\hat{x}_{k+1} - \hat{\mathbf{F}} \hat{x}_{k})}{\sum_{k=1}^{N} \hat{x}_{k}^{2}}.~ \end{equation}

　　关于参数估计收敛性已经有了很成熟的研究。[21][22][23][24]

9. 变体

　　目前已经提出了许多方法来加速 EM 算法，解决有时收敛速度缓慢的问题，例如使用共轭梯度和改进的牛顿方法(牛顿-拉夫森)。[25]此外，EM 算法还可以与约束估计方法一起使用。

　　参数扩展期望最大化算法通常通过 “利用‘协方差调整’来校正对 M 步的分析，强调估算的完整数据中捕获的额外信息” 来加速。[26]

　　期望条件最大化用一系列条件最大化(CM)步骤替换每个 M 步，其中每个参数 $\theta_i$ 在其他参数保持不变的情况下，有条件地单独最大化。[27]它可以扩展到期望条件最大化(ECME) 算法。[28]

　　这个想法是在广义期望最大化(GEM) 算法的基础上进一步扩展，正如 “作为最大化-最大化过程” 部分所述，其中 GEM 在 E 步和 M 步中都只寻求目标函数 F 的增加。[15]GEM 在分布式环境中进一步开发，并得到了不错的结果。[29]

　　也可以将 EM 算法视为 MM 算法的子类（最大化/最小化或最小化/最大化，取决于上下文）。[30]因此使用在更一般情况下开发的任何地方。

9.1 $\alpha$-EM 算法

　　 EM 算法中使用的 $Q$ 函数是基于对数似然的。因此，它被视为对数 EM 算法。对数似然的使用可以推广到α对数似然比。然后，使用 $\alpha$ 对数似然比和α散度的 $Q$ 函数可以与观测数据的 $\alpha$ 对数似然比的表示精确地等价。获得这个 $Q$ 函数是一个广义的 E 步骤。它的最大化是一个广义的 M 步。这一对被称为 $\alpha$-EM 算法[31]其中包含 log-EM 算法作为其子类。因此，松山靖夫的α-EM 算法是对数-EM 算法的精确推广。不需要计算梯度或海森矩阵。通过选择合适的 $\alpha$，$\alpha$-EM 算法算法比对数-EM 算法收敛速度更快。$\alpha$-EM 算法推导出了隐马尔可夫模型估计算法 $\alpha$-HMM 的更快版本。[32]

10. 与变分贝叶斯方法的关系

　　 EM 是一种部分非贝叶斯最大似然方法。它的最终结果给出了一个概率分布在整个潜变量(贝叶斯风格)连同一个点估计 $\theta$ (最大似然估计或后验模式)。这可能需要一个完全贝叶斯版本，给出概率分布 $\theta$ 和潜变量。贝叶斯推断方法就是简单地对待 $\theta$ 作为另一个潜在变量。在这个范例中，E 和 M 步之间的区别消失了。如果使用如上所述的分解 Q 近似(变分贝叶斯)，求解可以迭代每个潜在变量(现在包括 $\theta$ )并一次优化一个。现在，k 需要每次迭代的步骤，其中 k 是潜变量的号码。对于图形模型，这很容易做到，因为每个变量都是新的 Q 只依赖于它的马尔可夫毯，所以局部消息传递可以用于有效的推理。

11. 几何解释

　　在信息几何中，E 阶和 M 阶被解释为双仿射联络下的投影，称为 E 联络和 M 联络；也可以用这些术语来理解信息增益。

12. 例子

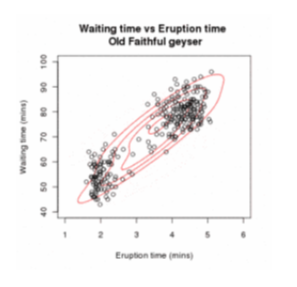
12.1 混合高斯分布

图 2：在人工生成的数据下，K-means 算法和#EM 算法的比较，由 ELKI 可视化。利用方差，EM 算法可以精确描述正态分布，而 K-means 算法将数据进行了一个 Voronoi 单元分割。聚类中心由其中最亮、最大的点所示。

图 3：EM 算法用两个混合高斯分布拟合旧的置信数据集的过程，用动图展示。算法从随机初始化到后来逐渐收敛。

　　 $\mathbf{x} = (\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n)$ 是两个 $d$ 维正态分布混合中的 $n$ 个独立观测的样本，$\mathbf{z} = (z_1, z_2, \ldots, z_n)$ 是决定观测起源的成分的潜变量。

\begin{align} X_i \mid (Z_i = 1) &\sim \mathcal{N}_d(\mu_1, \Sigma_1) \quad \text{和} \quad X_i \mid (Z_i = 2) \sim \mathcal{N}_d(\mu_2, \Sigma_2)~ \end{align}

　　其中

\begin{align} P(Z_i = 1) = \tau_1 \quad \text{和} \quad P(Z_i = 2) = \tau_2 = 1 - \tau_1~ \end{align}

　　目标是估计表示多个高斯分布中的混合值的未知参数与每个高斯分布的均值和协方差：

\begin{equation} \theta = (\tau, \mu_1, \mu_2, \Sigma_1, \Sigma_2)~, \end{equation}

其中不完全数据似然函数为 $$L(\theta; \mathbf{x}) = \prod_{i=1}^{n} \sum_{j=1}^{2} \tau_j f \left( x_i; \mu_j, \Sigma_j \right)~,$$ 完整数据似然函数为

\begin{equation} L(\theta; \mathbf{x}, \mathbf{z}) = p(\mathbf{x}, \mathbf{z} \mid \theta) = \prod_{i=1}^{n} \prod_{j=1}^{2} \left[ f(\mathbf{x}_i; \mu_j, \Sigma_j) \tau_j \right]^{\mathbb{I}(z_i = j)}~, \end{equation}

或者

\begin{equation} \mathcal{L}(\theta; \mathbf{x}, \mathbf{z}) = \exp \left\{\sum_{i=1}^{n} \sum_{j=1}^{2} \mathbb{I}(z_i = j)\left[\log \tau_j - \frac{1}{2} \log \lvert \Sigma_j \rvert - \frac{1}{2} (x_i - \mu_j)^\top \Sigma_j^{-1} (x_i - \mu_j) - \frac{d}{2} \log\left(2\pi\right) \right]\right\}~, \end{equation}

其中 $\mathbb{I}$ 是一个指示函数，$f$ 是多元正态分布的概率密度函数。

　　在最后的等式中，对于每一个 $i$，一个下标 $\mathbb{I}(z_i = j)$ 等于零，一个下标等于一。因此，内和减少到一项。

　　 E 步

　　根据我们目前对参数的估计 $\theta^{(t)}$，$z_i$ 的条件分布由贝叶斯法则确定，是权重为 $\tau$ 的正态密度的部分高度： $$T_{j,i}^{(t)} := \mathbb{P}(Z_i = j \mid X_i = x_i; \theta^{(t)}) = \frac{ \tau_j^{(t)} f(x_i; \mu_j^{(t)}, \Sigma_j^{(t)})}{ \tau_1^{(t)} f(x_i; \mu_1^{(t)}, \Sigma_1^{(t)}) + \tau_2^{(t)} f(x_i; \mu_2^{(t)}, \Sigma_2^{(t)}) }~.$$ 这些被称为 “成员概率”，通常被认为是 E 步的输出（尽管这不是下面的 Q 函数）。

　　该步骤对应于为 Q 的函数：

\begin{equation} \begin{aligned} Q(\theta \mid \theta^{(t)}) &= \mathbb{E}_{Z \mid X, \theta^{(t)}}[\log L(\theta; x, Z)] \\\\ &= \mathbb{E}_{Z \mid X, \theta^{(t)}}\left[\log \prod_{i=1}^{n} L(\theta; x_i, z_i)\right] \\\\ &= \mathbb{E}_{Z \mid X, \theta^{(t)}}\left[\sum_{i=1}^{n} \log L(\theta; x_i, z_i)\right] \\\\ &= \sum_{i=1}^{n} \mathbb{E}_{Z_i \mid X, \theta^{(t)}}[\log L(\theta; x_i, z_i)] \\\\ &= \sum_{i=1}^{n} \sum_{j=1}^{2} \mathbb{P}(Z_i = j \mid X_i = x_i; \theta^{(t)}) \log L(\theta_j; x_i, z_i) \\\\ &= \sum_{i=1}^{n} \sum_{j=1}^{2} T_{j,i}^{(t)} \left[\log \tau_j - \frac{1}{2} \log \lvert \Sigma_j \rvert - \frac{1}{2} (x_i - \mu_j)^\top \Sigma_j^{-1} (x_i - \mu_j) - \frac{d}{2} \log\left(2\pi\right) \right]~. \end{aligned} \end{equation}

　　在上述求和中，$\log L(\theta; x_i, z_i)$ 的期望是关于概率密度函数 $\mathbb{P}(Z_i \mid X_i = x_i; \theta^{(t)})$ 的，每个不同训练集 $x_i$ 的期望可能都不同。在采取步骤之前，E 步骤中的所有内容都是已知的，除了 $T_{j,i}$，它是根据 E 步骤开始时的公式计算的。

　　这个完全条件的期望不需要一步计算，因为 $\tau$ 和 $\sigma$ 以独立的线性项出现，因此可以独立地最大化。

　　 M 步

　　 $Q(\theta | \theta^{(t)})$ 在形式上是二次的，意味着确定 $\theta$ 相对简单。另外，$\tau, (\mu_1, \sigma_1)$ 和 $(\mu_2, \sigma_2)$ 都可以独立地最大化，因为它们都以单独的线性项出现。

　　首先，考虑 $\tau$，它有约束 $\tau_1 + \tau_2 = 1$:

\begin{equation} \begin{aligned} \tau^{(t+1)} &= \arg \max_{\tau} Q(\theta | \theta^{(t)}) \\\\ &= \arg \max_{\tau} \left\{ \left[ \sum_{i=1}^n T_{1,i}^{(t)} \right] \log \tau_1 + \left[ \sum_{i=1}^n T_{2,i}^{(t)} \right] \log \tau_2 \right\}~. \end{aligned} \end{equation}

这与二项分布的最大似然估计形式相同，所以 $$\tau_j^{(t+1)} = \frac{\sum_{i=1}^n \mathbf{T}_{j,i}^{(t)}}{\sum_{i=1}^n (\mathbf{T}_{1,i}^{(t)} + \mathbf{T}_{2,i}^{(t)})} = \frac{1}{n} \sum_{i=1}^n \mathbf{T}_{j,i}^{(t)}~.$$ 对于下一个估计 $(\mu_1, \Sigma_1)$:

\begin{equation} \begin{aligned} (\mu_1^{(t+1)}, \Sigma_1^{(t+1)}) &= \arg \max_{\mu_1, \Sigma_1} Q(\theta \mid \theta^{(t)})\\ &= \arg \max_{\mu_1, \Sigma_1} \sum_{i=1}^n \mathbf{T}_{1,i}^{(t)} \left\{ -\frac{1}{2} \log |\Sigma_1| - \frac{1}{2} (x_i - \mu_1)^\top \Sigma_1^{-1} (x_i - \mu_1) \right\}~. \end{aligned} \end{equation}

　　这与正态分布的加权最大似然估计形式相同，所以 $$\mu_1^{(t+1)} = \frac{\sum_{i=1}^n \mathbf{T}_{1,i}^{(t)} x_i}{\sum_{i=1}^n \mathbf{T}_{1,i}^{(t)}}\quad \text{和} \quad\Sigma_1^{(t+1)} = \frac{\sum_{i=1}^n \mathbf{T}_{1,i}^{(t)} (x_i - \mu_1^{(t+1)}) (x_i - \mu_1^{(t+1)})^\top}{\sum_{i=1}^n \mathbf{T}_{1,i}^{(t)}}~.$$ 对称地说 $$\mu_2^{(t+1)} = \frac{\sum_{i=1}^n \mathbf{T}_{2,i}^{(t)} x_i}{\sum_{i=1}^n \mathbf{T}_{2,i}^{(t)}}\quad \text{和} \quad\Sigma_2^{(t+1)} = \frac{\sum_{i=1}^n \mathbf{T}_{2,i}^{(t)} (x_i - \mu_2^{(t+1)}) (x_i - \mu_2^{(t+1)})^\top}{\sum_{i=1}^n \mathbf{T}_{2,i}^{(t)}}~.$$

　　结束

　　如果出现以下情况，则结束迭代过程 $E_{\mathbf{Z} \mid \theta^{(t)}, \mathbf{x}}[\log L(\theta^{(t)} ; \mathbf{x}, \mathbf{Z})] \leq E_{\mathbf{Z} \mid \theta^{(t-1)}, \mathbf{x}}[\log L(\theta^{(t-1)} ; \mathbf{x}, \mathbf{Z})] + \varepsilon$ 对于 $\varepsilon$ 低于某个预设阈值。

　　泛化

　　上述算法可以推广到两个以上多元正态分布的混合。

12.2 断尾回归和归并回归

　　 EM 算法已经应用在下面的线性回归模型存在时的情况，该模型解释了一些量的变化，但是实际观察到的值是模型中表示的值的删改或截断版本。[33]这种模型的特殊情况包括来自一个正态分布的删改或截断观测。[33]

13. 替代算法

　　 EM 通常收敛到局部最优，不一定是全局最优，一般情况下不限制收敛速度。它有可能在高维空间中是任意差的，并且可能有指数数量级的局部最优解。因此，需要替代方法来保证学习，特别是在高维环境中。新兴的替代方案在一致性方面有更好的保证，称为基于动量的方法或者所谓的光谱技术。基于动量的概率模型参数学习方法最近越来越受关注，因为它们在某些条件下享有全局收敛性等保证，而不像 EM 那样经常被陷入局部最优的问题而困扰。具有学习保证的算法可以被导出用于许多重要的模型，例如混合模型、隐马尔科夫模型等。对于这些谱方法，不会出现虚假的局部最优，并且在某些规则条件下可以一致地估计真实参数。

14. 参考文献

　　 [1] ^Dempster, A.P.; Laird, N.M.; Rubin, D.B. (1977). "Maximum Likelihood from Incomplete Data via the EM Algorithm". Journal of the Royal Statistical Society, Series B. 39 (1): 1–38. JSTOR 2984875. MR 0501537..

　　 [2] ^Ceppelini, R.M. (1955). "The estimation of gene frequencies in a random-mating population". Ann. Hum. Genet. 20 (2): 97–115. doi:10.1111/j.1469-1809.1955.tb01360.x..

　　 [3] ^See the acknowledgement by Dempster, Laird and Rubin on pages 3, 5 and 11..

　　 [4] ^G. Kulldorff. 1961. Contributions to the theory of estimation from grouped and partially grouped samples. Almqvist & Wiksell..

　　 [5] ^Anders Martin-Löf. 1963. "Utvärdering av livslängder i subnanosekundsområdet" ("Evaluation of sub-nanosecond lifetimes"). ("Sundberg formula").

　　 [6] ^Per Martin-Löf. 1966. Statistics from the point of view of statistical mechanics. Lecture notes, Mathematical Institute, Aarhus University. ("Sundberg formula" credited to Anders Martin-Löf)..

　　 [7] ^Per Martin-Löf. 1970. Statistika Modeller (Statistical Models): Anteckningar från seminarier läsåret 1969–1970 (Notes from seminars in the academic year 1969-1970), with the assistance of Rolf Sundberg. Stockholm University. ("Sundberg formula").

　　 [8] ^Martin-Löf, P. The notion of redundancy and its use as a quantitative measure of the deviation between a statistical hypothesis and a set of observational data. With a discussion by F. Abildgård, A. P. Dempster, D. Basu, D. R. Cox, A. W. F. Edwards, D. A. Sprott, G. A. Barnard, O. Barndorff-Nielsen, J. D. Kalbfleisch and G. Rasch and a reply by the author. Proceedings of Conference on Foundational Questions in Statistical Inference (Aarhus, 1973), pp. 1–42. Memoirs, No. 1, Dept. Theoret. Statist., Inst. Math., Univ. Aarhus, Aarhus, 1974..

　　 [9] ^Martin-Löf, Per (1974). "The notion of redundancy and its use as a quantitative measure of the discrepancy between a statistical hypothesis and a set of observational data". Scand. J. Statist. 1 (1): 3–18..

　　 [10] ^Sundberg, Rolf (1974). "Maximum likelihood theory for incomplete data from an exponential family". Scandinavian Journal of Statistics. 1 (2): 49–58. JSTOR 4615553. MR 0381110..

　　 [11] ^Rolf Sundberg. 1971. Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable. Dissertation, Institute for Mathematical Statistics, Stockholm University..

　　 [12] ^Sundberg, Rolf (1976). "An iterative method for solution of the likelihood equations for incomplete data from exponential families". Communications in Statistics – Simulation and Computation. 5 (1): 55–64. doi:10.1080/03610917608812007. MR 0443190..

　　 [13] ^Wu, C. F. Jeff (Mar 1983). "On the Convergence Properties of the EM Algorithm". Annals of Statistics. 11 (1): 95–103. doi:10.1214/aos/1176346060. JSTOR 2240463. MR 0684867..

　　 [14] ^Little, Roderick J.A.; Rubin, Donald B. (1987). Statistical Analysis with Missing Data. Wiley Series in Probability and Mathematical Statistics. New York: John Wiley & Sons. pp. 134–136. ISBN 978-0-471-80254-9..

　　 [15] ^Neal, Radford; Hinton, Geoffrey (1999). Michael I. Jordan, ed. A view of the EM algorithm that justifies incremental, sparse, and other variants (PDF). Learning in Graphical Models. Cambridge, MA: MIT Press. pp. 355–368. ISBN 978-0-262-60032-3. Retrieved 2009-03-22..

　　 [16] ^Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2001). "8.5 The EM algorithm". The Elements of Statistical Learning. New York: Springer. pp. 236–243. ISBN 978-0-387-95284-0..

　　 [17] ^Lindstrom, Mary J; Bates, Douglas M (1988). "Newton—Raphson and EM Algorithms for Linear Mixed-Effects Models for Repeated-Measures Data". Journal of the American Statistical Association. 83 (404): 1014. doi:10.1080/01621459.1988.10478693..

　　 [18] ^Van Dyk, David A (2000). "Fitting Mixed-Effects Models Using Efficient EM-Type Algorithms". Journal of Computational and Graphical Statistics. 9 (1): 78–98. doi:10.2307/1390614. JSTOR 1390614..

　　 [19] ^Diffey, S. M; Smith, A. B; Welsh, A. H; Cullis, B. R (2017). "A new REML (parameter expanded) EM algorithm for linear mixed models". Australian & New Zealand Journal of Statistics. 59 (4): 433. doi:10.1111/anzs.12208..

　　 [20] ^Matarazzo, T. J., and Pakzad, S. N. (2016). “STRIDE for Structural Identification using Expectation Maximization: Iterative Output-Only Method for Modal Identification.” Journal of Engineering Mechanics.http://ascelibrary.org/doi/abs/10.1061/(ASCE)EM.1943-7889.0000951.

　　 [21] ^Einicke, G.A.; Malos, J.T.; Reid, D.C.; Hainsworth, D.W. (January 2009). "Riccati Equation and EM Algorithm Convergence for Inertial Navigation Alignment". IEEE Trans. Signal Process. 57 (1): 370–375. Bibcode:2009ITSP...57..370E. doi:10.1109/TSP.2008.2007090..

　　 [22] ^Einicke, G.A.; Falco, G.; Malos, J.T. (May 2010). "EM Algorithm State Matrix Estimation for Navigation". IEEE Signal Processing Letters. 17 (5): 437–440. Bibcode:2010ISPL...17..437E. doi:10.1109/LSP.2010.2043151..

　　 [23] ^Einicke, G.A.; Falco, G.; Dunn, M.T.; Reid, D.C. (May 2012). "Iterative Smoother-Based Variance Estimation". IEEE Signal Processing Letters. 19 (5): 275–278. Bibcode:2012ISPL...19..275E. doi:10.1109/LSP.2012.2190278..

　　 [24] ^Einicke, G.A. (Sep 2015). "Iterative Filtering and Smoothing of Measurements Possessing Poisson Noise". IEEE Transactions on Aerospace and Electronic Systems. 51 (3): 2205–2011. Bibcode:2015ITAES..51.2205E. doi:10.1109/TAES.2015.140843..

　　 [25] ^Jamshidian, Mortaza; Jennrich, Robert I. (1997). "Acceleration of the EM Algorithm by using Quasi-Newton Methods". Journal of the Royal Statistical Society, Series B. 59 (2): 569–587. doi:10.1111/1467-9868.00083. MR 1452026..

　　 [26] ^Liu, C (1998). "Parameter expansion to accelerate EM: The PX-EM algorithm". Biometrika. 85 (4): 755–770. CiteSeerX 10.1.1.134.9617. doi:10.1093/biomet/85.4.755..

　　 [27] ^Meng, Xiao-Li; Rubin, Donald B. (1993). "Maximum likelihood estimation via the ECM algorithm: A general framework". Biometrika. 80 (2): 267–278. doi:10.1093/biomet/80.2.267. MR 1243503..

　　 [28] ^Liu, Chuanhai; Rubin, Donald B (1994). "The ECME Algorithm: A Simple Extension of EM and ECM with Faster Monotone Convergence". Biometrika. 81 (4): 633. doi:10.2307/2337067. JSTOR 2337067..

　　 [29] ^Jiangtao Yin; Yanfeng Zhang; Lixin Gao (2012). "Accelerating Expectation-Maximization Algorithms with Frequent Updates" (PDF). Proceedings of the IEEE International Conference on Cluster Computing..

　　 [30] ^Hunter DR and Lange K (2004), A Tutorial on MM Algorithms, The American Statistician, 58: 30-37.

　　 [31] ^Matsuyama, Yasuo (2003). "The α-EM algorithm: Surrogate likelihood maximization using α-logarithmic information measures". IEEE Transactions on Information Theory. 49 (3): 692–706. doi:10.1109/TIT.2002.808105..

　　 [32] ^Matsuyama, Yasuo (2011). "Hidden Markov model estimation based on alpha-EM algorithm: Discrete and continuous alpha-HMMs". International Joint Conference on Neural Networks: 808–816..

　　 [33] ^Wolynetz, M.S. (1979). "Maximum likelihood estimation in a linear model from confined and censored normal data". Journal of the Royal Statistical Society, Series C. 28 (2): 195–206. doi:10.2307/2346749. JSTOR 2346749..