域上的代数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学中，一个域上的代数（通常简称为代数，algebra）是一个带有双线性乘法的向量空间。因此，代数是一种代数结构，由一个集合以及加法、乘法和域元素的数量乘法构成，并且满足 “向量空间” 和 “双线性” 所蕴含的公理。\(^\text{[1]}\)

　　 代数中的乘法运算可以是结合的，也可以不是，这对应于结合代数（假设乘法具有结合性）和非结合代数（不假设乘法具有结合性，但也不排除结合性）。例如，给定一个整数 $n$，实数域上的 $n$ 阶实方阵环，在矩阵加法和矩阵乘法下，是一个结合代数，因为矩阵乘法是结合的。另一方面，三维欧几里得空间在向量叉积运算下是一个非结合代数，因为向量叉积不满足结合律，但满足雅可比恒等式。

　　 如果代数在乘法下具有单位元，则称其为有单位代数。例如，$n$ 阶实方阵环是一个有单位代数，因为 $n$ 阶单位矩阵是矩阵乘法的单位元。它是一个有单位结合代数的例子，即既是（有单位的）环，又是一个向量空间。

　　 许多作者使用 “代数” 一词时，实际上是指结合代数，或有单位结合代数，或者在某些学科（如代数几何）中，指有单位结合交换代数。

　　 将标量的域替换为交换环，就得到了更一般的环上的代数的概念。需要注意的是，代数不同于带双线性型的向量空间（如内积空间），因为对于这样的空间，乘积的结果不在空间本身，而是在系数域中。

1. 定义与动机

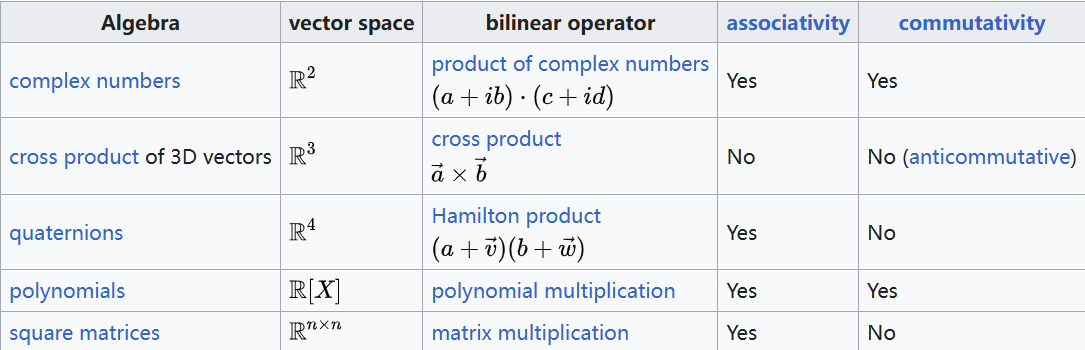
动机性示例

图
图 1

定义

　　 设 $K$ 是一个域，$A$ 是一个定义在 $K$ 上的向量空间，并且带有一个从 $A \times A$ 到 $A$ 的附加二元运算，记作 $\cdot$（也就是说，若 $x$ 和 $y$ 是 $A$ 的任意两个元素，则 $x \cdot y$ 是 $A$ 的一个元素，称为 $x$ 和 $y$ 的积）。若对所有 $A$ 中的元素 $x, y, z$ 以及所有 $K$ 中的元素（通常称为标量）$a, b$，以下恒等式成立，则称 $A$ 是一个定义在 $K$ 上的代数：

　　 这三个公理等价于说二元运算是双线性的。一个定义在 $K$ 上的代数有时也称为 $K$-代数，而 $K$ 被称为 $A$ 的基域。这个二元运算通常被称为 $A$ 的乘法。本文所采用的约定是：代数中元素的乘法不一定满足结合律，尽管有些作者使用 “代数” 一词时默认指结合代数。

　　 当向量空间上的二元运算是交换的情况下，左分配律与右分配律是等价的，此时只需证明一个分配律即可。一般而言，对于非交换运算，左分配律与右分配律并不等价，必须分别证明。

2. 基本概念

代数同态

　　 给定两个 $K$-代数 $A$ 和 $B$，一个 $K$-代数同态是一个 $K$-线性映射 $f: A \to B$ 使得对所有 $x, y \in A$ 都有 $f(xy) = f(x) f(y)$。如果 $A$ 和 $B$ 是有单位元的代数，并且一个同态满足 $f(1_A) = 1_B$，则称它为一个有单位同态。所有从 $A$ 到 $B$ 的 $K$-代数同态所构成的集合通常记作 $$ \mathbf{Hom}_{K\text{-alg}}(A, B)~ $$ 一个 $K$-代数同构是一个双射的 $K$-代数同态。

子代数与理想

　　 一个定义在域 $K$ 上的代数的子代数是一个线性子空间，具有这样的性质：其任意两个元素的积仍然属于该子空间。换句话说，代数的子代数是一个在加法、乘法和数量乘法下封闭的非空元素子集。用符号表示，如果 $A$ 是一个 $K$-代数，当 $L \subseteq A$ 且对所有 $x, y \in L$ 和 $c \in K$ 有 $x \cdot y \in L \quad x + y \in L \quad cx \in L$ 则称 $L$ 是 $A$ 的一个子代数。

　　 在前面将复数视为实数域上的二维代数的例子中，一维的实数直线就是一个子代数。

　　 一个 $K$-代数的左理想是一个线性子空间，具有这样的性质：其任意一个元素被代数中任意一个元素从左边相乘，结果仍然属于该子空间。用符号表示，如果 $A$ 是一个 $K$-代数，当 $L \subseteq A$ 且对所有 $x, y \in L$、$z \in A$、$c \in K$，以下三个条件成立时，称 $L$ 是一个左理想：

  1. $x + y \in L$（$L$ 在加法下封闭）；
  2. $cx \in L$（$L$ 在数量乘法下封闭）；
  3. $z \cdot x \in L$（$L$ 在任意元素的左乘下封闭）。

　　 如果将 (3) 替换为 $x \cdot z \in L$，则定义的是一个右理想。一个双边理想是既是左理想又是右理想的子集。通常单独使用 “理想” 一词时，指的是双边理想。当然，当代数是交换的时，这些理想的概念是等价的。条件 (1) 和 (2) 一起等价于 $L$ 是 $A$ 的一个线性子空间，由条件 (3) 可知每个左理想或右理想都是一个子代数。

　　 这个定义与环的理想定义不同，因为这里我们需要条件 (2)。当然，如果代数是有单位的，则条件 (3) 推出条件 (2)。

标量的扩张

　　 如果我们有一个域扩张 $F/K$，也就是说一个包含 $K$ 的更大的域 $F$，那么可以通过一种自然的方法，从任意一个定义在 $K$ 上的代数构造出一个定义在 $F$ 上的代数。这和将向量空间扩张到更大域上的方法是一样的，即使用张量积：$V_F := V \otimes_K F $。因此，如果 $A$ 是一个定义在 $K$ 上的代数，那么 $A_F$ 就是一个定义在 $F$ 上的代数。

3. 代数的种类与示例

　　 定义在域上的代数有很多不同的类型。这些类型由一些进一步的公理决定，例如乘法的交换性或结合性，而这些在代数的广义定义中并不是必须的。不同类型的代数对应的理论往往非常不同。

有单位代数

　　 如果一个代数具有单位元或恒等元 $I$，并且对代数中所有的 $x$ 都满足 $I x = x = x I$，则称该代数是有单位代数。

零代数

　　 如果一个代数中对所有 $u, v$ 都有 $uv = 0$，则称它为零代数，\(^\text{[2]}\) 不要与 “只有一个元素的代数” 混淆。零代数本质上是非幺的（除非只有一个元素的情形），并且是结合的、交换的。

　　 一个幺零代数是一个域 $K$ 与一个 $K$-向量空间 $V$ 的直和 $K \oplus V$，其乘法在向量空间（或模）上恒为零，并使其成为一个有单位元的代数。

　　 更确切地说，代数的每个元素都可以唯一地写为 $k + v, \quad k \in K, v \in V,$ 并且乘法是唯一的双线性运算，满足对所有 $v, w \in V$：$vw = 0$.因此，若 $k_1, k_2 \in K$ 且 $v_1, v_2 \in V$，则有： $$ (k_1 + v_1)(k_2 + v_2) = k_1k_2 + (k_1v_2 + k_2v_1)~ $$ 一个经典的幺零代数的例子是对偶数代数，它是由一个一维实向量空间构造出的幺零 $\mathbb{R}$-代数。

　　 这个定义可以直接推广到交换环上的幺零代数，将 “域” 和 “向量空间” 分别替换为 “交换环” 和 “模”。

　　 幺零代数允许统一给定模的子模理论和幺代数的理想理论。事实上，一个模 $V$ 的子模正好对应于包含在 $K \oplus V$ 中的理想。

　　 例如，Gröbner 基理论是 Bruno Buchberger 为域上的多项式环 $R = K[x_1,\dots, x_n]$ 中的理想引入的。通过在自由 $R$-模上构造幺零代数，可以将这一理论推广为自由模的子模的 Gröbner 基理论。这一推广使得在计算子模的 Gröbner 基时，可以不加修改地使用任何计算理想 Gröbner 基的算法和软件。

　　 类似地，幺零代数可以直接推出模（交换环上的模）的 Lasker–Noether 定理，而无需额外的证明，只需从原本针对理想的 Lasker–Noether 定理出发即可。

结合代数

　　 结合代数的例子包括：

非结合代数

　　 一个非结合代数 \(^\text{[3]}\)（或称分配代数，distributive algebra）是一个定义在域 $K$ 上的 $K$-向量空间 $A$，配备了一个 $K$-双线性映射 $A \times A \to A$。这里 “非结合” 的含义是不假设结合律成立，但并不意味着结合律被禁止，即 “非必然结合”。

　　 主条目中详细介绍的例子包括：

4. 代数与环

　　 结合的、有单位元的 $K$-代数的定义也经常以另一种方式给出。在这种情况下，域 $K$ 上的一个代数 $A$ 被定义为一个环，并带有一个环同态： $$ \eta : K \to Z(A)~ $$ 其中 $Z(A)$ 是 $A$ 的中心。由于 $\eta$ 是一个环同态，所以必须满足：要么 $A$ 是零环，要么 $\eta$ 是单射。

　　 该定义与前面的定义是等价的，其中标量乘法 $$ K \times A \to A~ $$ 由下式给出： $$ (k, a) \mapsto \eta(k)a~ $$ 给定两个这样的结合的、有单位的 $K$-代数 $A$ 和 $B$，一个有单位的 $K$-代数同态 $f : A \to B$ 是一个与 $\eta$ 所定义的标量乘法可交换的环同态，可以写作： $$ f(ka) = k f(a)~ $$ 对所有 $k \in K$ 和 $a \in A$ 都成立。换句话说，下列图表是可交换的： $$ \begin{matrix} & & K & & \\ & \eta_A \swarrow & & \eta_B \searrow & \\ A & & \xrightarrow{f} & & B \end{matrix}~ $$

5. 结构系数

　　 对于域上的代数，从 $A \times A \to A$ 的双线性乘法完全由 $A$ 的基元素的乘法决定。反过来，一旦选定了 $A$ 的一个基，就可以任意规定基元素的乘积，然后以唯一的方式将其扩展为 $A$ 上的双线性算子，即保证所得的乘法满足代数公理。

　　 因此，给定域 $K$，任意有限维代数可以通过给出它的维数（设为 $n$）并指定 $n^3$ 个结构系数 $c_{i,j,k}$（这些是标量）来确定到同构为止。这些结构系数通过如下规则确定 $A$ 中的乘法： $$ \mathbf{e}_i \mathbf{e}_j = \sum_{k=1}^{n} c_{i,j,k} \mathbf{e}_k,~ $$ 其中 $\mathbf{e}_1, \ldots, \mathbf{e}_n$ 构成 $A$ 的一个基。

　　 需要注意的是，几个不同的结构系数组合可能会导出同构的代数。

　　 在数学物理中，结构系数通常带上下标书写，以区分它们在坐标变换下的变换性质。具体来说，下标是协变指标，通过拉回变换，而上标是逆变指标，通过推前变换。因此，结构系数通常写作 $c_{i,j}{}^{k}$，其定义规则用爱因斯坦求和约定可写作： $$ e_i e_j = c_{i,j}{}^{k} e_k.~ $$ 将此应用于用指标表示的向量时，可得： $$ (xy)^k = c_{i,j}{}^{k} x^i y^j.~ $$ 如果 $K$ 只是一个交换环而不是一个域，当 $A$ 是 $K$ 上的自由模时，同样的过程仍然成立。如果不是自由模，则乘法仍然完全由它在一个生成 $A$ 的集合上的作用决定；但是在这种情况下，结构常数不能随意指定，仅知道结构常数并不能唯一确定代数的同构类。

6. 复数域上低维有单位结合代数的分类

　　 二维、三维和四维的复数域上有单位结合代数在同构意义下由 Eduard Study 完全分类。\(^\text{[5]}\)

　　 二维代数

　　 存在两个这样的二维代数。每个代数由两个基元素 $1$（单位元）和 $a$ 的复数系数线性组合组成。根据单位元的定义： $$ 1 \cdot 1 = 1, \quad 1 \cdot a = a, \quad a \cdot 1 = a.~ $$ 剩下需要指定：
对于第一个代数：$a a = 1$
对于第二个代数：$a a = 0$

　　 三维代数

　　 存在五个这样的三维代数。每个代数由三个基元素 $1$（单位元）、$a$ 和 $b$ 的复数系数线性组合组成。考虑单位元的定义，只需指定：
第一个代数：$a a = a, \quad b b = b, \quad a b = b a = 0$
第二个代数：$a a = a, \quad b b = 0, \quad a b = b a = 0$
第三个代数：$a a = b, \quad b b = 0, \quad a b = b a = 0$
第四个代数：$a a = 1, \quad b b = 0, \quad a b = - b a = b$
第五个代数：$a a = 0, \quad b b = 0, \quad a b = b a = 0$
其中，第四个代数是非交换的，其余都是交换的。

7. 推广：环上的代数

　　 在数学的一些领域（例如交换代数）中，通常会考虑更一般的概念——环上的代数，其中用一个交换环 $R$ 替换域 $K$。定义中唯一改变的是：假设 $A$ 是一个 $R$-模（而不是 $K$-向量空间）。

环上的结合代数

　　 一个环 $A$ 总是它的中心上的结合代数，同时也是整数环 $\mathbb{Z}$ 上的结合代数。一个经典的 “在其中心上的代数” 例子是分裂双四元数代数，它同构于 $\mathbb{H} \times \mathbb{H}$ 即两个四元数代数的直积。该环的中心是 $\mathbb{R} \times \mathbb{R}$ 因此它具有在其中心上的代数结构，而其中心并不是一个域。注意，分裂双四元数代数也天然是一个 8 维的 $\mathbb{R}$-代数。

　　 在交换代数中，如果 $A$ 是一个交换环，则任何一个有单位的环同态 $R \to A$ 都会在 $A$ 上定义一个 $R$-模结构，这就是所谓的 $R$-代数结构。[5] 因此，一个环天然带有一个 $\mathbb{Z}$-模结构，因为可以取唯一的同态 $\mathbb{Z} \to A$。\(^\text{[6]}\) 另一方面，并不是所有环都能被赋予一个域上的代数结构（例如整数环 \(\mathbb{Z}\) 就不行）。关于尝试给每个环一个像域上代数一样行为的结构，请参见 “特征为 1 的域” 的描述。

8. 另见

9. 注释

  1. 另见 Hazewinkel, Gubareni & Kirichenko 2004，第 3 页，命题 1.1.1
  2. Prolla, João B. (2011) [1977]. "引理 4.10". Approximation of Vector Valued Functions. Elsevier. 第 65 页, ISBN 978-0-08-087136-3.
  3. Schafer, Richard D. (1996). An Introduction to Nonassociative Algebras*. Courier Corporation. ISBN 0-486-68813-5.
  4. Study, E. (1890). "Über Systeme complexer Zahlen und ihre Anwendungen in der Theorie der Transformationsgruppen", *Monatshefte für Mathematik, 1 (1): 283–354, doi:10.1007/BF01692479, S2CID 121426669.
  5. Matsumura, H. (1989). Commutative Ring Theory. Cambridge Studies in Advanced Mathematics. 第 8 卷. M. Reid 翻译（第 2 版）. Cambridge University Press. ISBN 978-0-521-36764-6.
  6. Kunz, Ernst (1985). Introduction to Commutative Algebra and Algebraic Geometry. Birkhauser. ISBN 0-8176-3065-1.

10. 参考文献

                     

© 保留一切权利