引力波(综述)
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
引力波是时空曲率中的扰动,由加速的质量所产生,并以光速从源头向外传播。它们是由 Henri Poincaré在 1905 年提出的[1],后来在 1916 年被爱因斯坦根据他的广义相对论所预测。[2][3][4] 引力波以引力辐射的形式传输能量,这是一种类似于电磁辐射的辐射能。[5] 作为经典力学的一部分,牛顿的万有引力定律并没有规定它们(引力波)的存在,因为该定律是基于物理相互作用瞬时(以无限大速度)传播的假设,这展示了经典物理学方法无法解释相对论现象的一个例子。
引力波天文学是观测天文学的一个分支,它使用引力波来收集关于可探测引力波来源的观测数据,例如由白矮星、中子星和黑洞组成的双星系统,和超新星等事件,以及大爆炸后不久的早期宇宙的形成。
1993 年,Russell A. Hulse 和 Joseph H. Taylor, Jr.因为发现和观测赫尔斯-泰勒双星而获得诺贝尔物理学奖,这是引力波存在的第一个间接证据。[6]
2016 年 2 月 11 日,激光干涉引力波天文台和处女座干涉仪科学合作组织宣布他们首次直接观测到引力波。这一观察发生在五个月前,即 2015 年 9 月 14 日,在这次观测中使用了增进 LIGO 探测器。这次事件的引力波起源于一对合并的黑洞。在第一次探测到引力波的消息宣布之后,激光干涉引力波天文台的仪器又探测到了两次确认的引力波事件以及一次潜在的引力波事件。[7][8] 2017 年 8 月,两个激光干涉引力波天文台的仪器和处女座干涉仪观测到第四次来自合并黑洞的引力波,[9] 和来自双星合并的第五次引力波。另外几个引力波探测器正在计划或建造中。[10]
2017 年,Rainer Weiss、Kip Thorne 和 Barry Barish 因他们在引力波直接探测中所作的贡献而获得了诺贝尔物理学奖。
1. 介绍
在爱因斯坦的广义相对论中,引力被视为时空曲率导致的一种现象。这种曲率是由质量的存在所引起的。一般来说,在一个给定体积的空间中包含的质量越大,其边界处的时空曲率就越大。[11] 当有质量的物体在时空中移动时,曲率会发生改变,反映出这些物体位置的变化。在某些情况下,加速的物体会引发曲率的变化,并以波的形式向外以光速传播。这些传播现象被称为引力波。
当引力波经过观察者时,观察者会发现时空被应变的影响扭曲了。物体之间的距离随着波的传播有节奏地增加和减少,频率等于波的频率。尽管这些自由物体从未受到不平衡的力的作用,这种情况还是会发生。这种效应的大小与其跟引力波源的距离成反比。[12] 由于它们的质量在它们彼此靠近的轨道上有非常大的加速度,互相螺旋靠近合并的双中子星被预测为引力波的强大来源。然而,由于我们与这些辐射源之间巨大的天文距离,在地球上测量到的影响预计非常小,应变不到 $1/10^{20}$。科学家已经用越来越灵敏的探测器证明了这些波的存在。最灵敏的探测器完成了由 LIGO 和 VIRGO 天文台提供的 $1/{5 \times 10^{22}}$ 截至 2012 年)的灵敏度测量任务。[13] 欧洲空间局目前正在开发一个名为激光干涉空间天线的空基天文台。
引力波可以穿透电磁波无法穿透的空间区域。它们能被用于观察黑洞合并以及遥远宇宙中可能存在的其他奇异物体的合并。这样的系统不能用更传统的方法来观察,比如光学望远镜或射电望远镜,因此引力波天文学为宇宙的运作提供了新的洞察。特别地,引力波可能是宇宙学家感兴趣的,因为它们提供了观察非常早期宇宙的可能的方法。这在传统天文学中是不可能的,因为在复合之前,宇宙对电磁辐射是不透明的。[14] 引力波的精确测量也将使科学家能够更彻底地测试广义相对论。
原则上,引力波可以以任何频率存在。然而,非常低频的引力波是不可能被检测到的,而且也没有非常高频的可探测引力波的可靠来源。Stephen Hawking 和 Werner Israel 列出了引力波的不同频段,这些频段可能被探测到,范围从 $ 10^{-7}$ 赫兹一直到 $ 10^{11}$ 赫兹。
2. 历史
1893 年,Oliver Heaviside 用重力和电的平方反比定律之间的类比讨论了引力波的可能性。[15] 1905 年,Henri Poincaré根据洛伦兹变换的要求,提出了从物体发出并以光速传播的引力波,[16] 并建议,类似于加速电荷产生电磁波,相对论性引力场论中的加速质量应产生引力波。[17][18] 当爱因斯坦在 1915 年发表他的广义相对论时,他对 Poincaré的想法持怀疑态度,因为该理论暗示不存在 “引力偶极子”。尽管如此,他仍然考虑了这个想法,并根据各种近似得出结论:事实上,引力波必须有三种类型(赫尔曼·外尔称之为纵向-纵向、横向-纵向和横向-横向)。[18]
然而,爱因斯坦所做的近似导致许多人(包括爱因斯坦本人)怀疑这个结果。1922 年,Arthur Eddington 证明了爱因斯坦的两种波是他所使用的坐标系的赝像,可以通过选择合适的坐标使得其任何速度传播,这导致爱丁顿开玩笑说它们 “以思想的速度传播”。[19] 这也使得人们对第三种引力波类型(横向-横向)的物理实在性提出了质疑,Eddington 证明了这种类型的引力波总是以光速传播,跟坐标系的选择无关。1936 年,爱因斯坦和 Nathan Rosen 向《物理评论》提交了一篇论文,在这篇论文中他们声称引力波不可能存在于完整的广义相对论中,因为场方程的任何这样的解都有奇点。该杂志将他们的手稿送交 Howard P. Robertson 审阅,他匿名报告说,爱因斯坦和 Rosen 所讨论的奇点仅仅是源于他们所使用的圆柱坐标的无害的坐标奇点。不熟悉同行评审的概念的爱因斯坦愤怒地撤回了手稿,再也没有在《物理评论》上发表文章。尽管如此,他的助手 Leopold Infeld(曾与 Robertson 联系过)还是让爱因斯坦相信了这一批评是正确的。这篇论文后来被用相反的结论重写了,并在其他地方发表。[18][19]
1956 年,Felix Pirani 通过用明显可见的黎曼曲率张量来重新表述引力波,纠正了使用各种坐标系造成的混乱。当时这项工作被大多数人忽视,因为科学共同体关注的是一个不同的问题:引力波是否能传输能量。这个问题是由 Richard Feynman 在 1957 年教堂山的第一次 “GR” 会议上提出的一个思想实验所解决的。简而言之,Feynman 那个被称为 “粘珠论证” 的论证指出,如果一个人拿着一根带有珠子的棒,那么经过的引力波的作用将是沿着棒移动珠子;摩擦会产生热量,这就意味着经过的波做功了。不久之后,曾经的引力波怀疑者 Hermann Bondi 发表了 “粘珠论证” 的详细版本。[18]
教堂山会议后,Joseph Weber 开始设计和建造第一个引力波探测器,现在它被称为韦伯棒。1969 年,Weber 声称已经探测到第一个引力波,到 1970 年,他已经 “探测” 到有规律地来自银心的信号;然而,探测的频率很快引起了人们对他的观测的有效性的怀疑,因为根据 Weber 的观测结果所推断的银河系能量损失率会在比推断的银河系年龄短得多的时间尺度上耗尽我们银河系的能量。到 20 世纪 70 年代中期,当其他研究组在世界各地建立自己的韦伯棒并进行反复实验却未能找到任何信号时,人们对 Weber 的观测结果的怀疑更强烈了。到了 70 年代后期,普遍的共识是 Weber 的结果是站不住脚的。[18]
在同一时期,引力波存在的第一个间接证据被发现了。1974 年,Russell Alan Hulse 和 Joseph Hooton Taylor, Jr.发现了第一颗双星,这一发现为他们赢得了 1993 年的诺贝尔物理学奖。在接下来的十年里,脉冲星计时观测显示赫尔斯-泰勒脉冲星的轨道周期逐渐衰减,这与广义相对论所预测的引力辐射所带来的能量和角动量损失相吻合。[20][18]
尽管 Weber 的结果不可信,但这种引力波的间接探测激发了进一步的研究。一些团体继续改进 Weber 最初的概念,而另一些团体则使用激光干涉仪来探测引力波。使用激光干涉仪探测引力波的想法似乎是由不同的人独立提出的,包括 1962 年的 M. E. Gertsenshtein 和 V. I. Pustovoit,[21] 以及 1966 年的 Vladimir B. Braginskiĭ。Robert L. Forward 和 Rainer Weiss 在 20 世纪 70 年代开发了第一批原型。[22][23] 在接下来的几十年里,越来越敏感的仪器被建造了出来,最终我们有了 GEO600、激光干涉引力波天文台和处女座干涉仪。[18]
经过多年的零结果,改进后的探测器于 2015 年投入使用——激光干涉引力波天文台于 2015 年 9 月 14 日首次直接探测到引力波。据推断,这个被称为 GW150914 的信号起源于两个质量分别为 36+4−4M⊙ 和 29+4−4 M⊙的黑洞的合并,最终得到一个质量为 62+4−4 M⊙的黑洞。这表明引力波信号携带了大约 3 个太阳质量的能量,这大约是 $ 5\times10^{47}$ 焦耳。[24][24][24]
一年前,当 BICEP2 声称他们在宇宙微波背景中探测到引力波的印记时,激光干涉引力波天文台似乎被击败了。然而,BICEP2 后来被迫撤回了他们的结果。[24][25]
2017 年,Rainer Weiss、Kip Thorne 和 Barry Barish 因在引力波探测中的所作出的贡献而获得了诺贝尔物理学奖。[26][26][26]
3. 引力波经过时的影响
引力波不断通过地球;然而,即使是最强的引力波也只有很小的影响,它们的波源通常距我们很远。例如,由 GW150914 事件中灾难性的最终合并所发出的引力波在经过十亿光年后到达地球,作为时空中的涟漪,它使得一个 4 公里长的激光干涉引力波天文台臂的长度改变了一个质子宽度的千分之一,这按比例相当于使我们到太阳系外最近的恒星的距离改变了一根头发的宽度。[26] 即使是极端引力波,它们的这种微小效应也只能被最精密的探测器在地球上探察到。
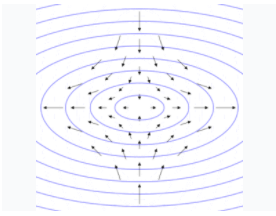
通过想象一个完全平坦的时空区域,在其中一组静止的测试粒子位于一个平面上(例如计算机屏幕的表面),我们可以看到一个极其夸张的引力波通过的效果。当引力波沿着垂直于粒子所在平面的直线穿过粒子时(即沿着观察者进入屏幕的视线),粒子将跟随时空扭曲以 “十字形” 的方式发生振荡,如动画所示。被测试粒子包围的区域面积不变,并且没有沿着引力波传播方向的运动。[来源请求]
出于讨论的目的,动画中描绘的振荡被夸大了。在现实中,引力波的振幅非常小(正如线性引力所描述的)。然而,它们有助于说明与在圆形轨道上运动的一对质量所产生的引力波相关的振荡。在这种情况下,引力波的振幅是恒定的,但是它的偏振面以两倍于轨道速度的速度变化或旋转,所以时变引力波的大小(或称 “周期性时空应变”)如动画所示表现出变化。[27] 如果质量的轨道是椭圆形的,那么根据爱因斯坦的四极子公式,引力波的振幅也会随着时间而变化。[28]
与其他波一样,引力波由如下这些特征所描述:
- 振幅: 通常表示为 $h$,这是波的大小,即动图中拉伸或挤压的部分。这里显示的振幅大致是 $h = 0.5$(或 50
%)。穿过地球的引力波比这个弱很多倍($h \approx 10^{-20}$)。 - 频率: 通常表示为 $f$,这是波振荡的频率(1 除以两次连续最大拉伸或挤压之间的时间)。
- 波长: 通常表示为 $\lambda$,这是沿着波方向的最大拉伸或挤压点之间的距离。
- 速度: 这是波上的一点(例如,最大拉伸或挤压点)行进的速度。对于小振幅的引力波,这个波速等于光速($c$)。
引力波的速度、波长和频率由下式联系起来:$c = \lambda f$,这跟电磁波的方程是一样的。例如,这里显示的动画大约每两秒振荡一次。这对应着 0.5 赫兹的频率以及约 600 000 公里的波长(地球直径的约 47 倍)。
在上面的例子中,我们假设波被线性极化为 “正” 极化,记作 $h_+$。引力波的极化就像光波的极化一样,区别在于引力波的极化是相隔 45 度而不是 90 度。[来源请求] 特别是在 “交叉” 极化的引力波(记作 $h_\times$)的例子中,引力波对测试粒子的影响与 “正” 极化的情况基本相同,但是旋转了 45 度(如第二个动画所示)。正如光偏振一样,引力波的偏振也可以用圆偏振波表示。引力波极化的根源是其波源的性质。
4. 来源
一般而言,引力波由运动涉及加速度及其变化的物体所辐射,前提是该运动不是完美的球对称(像膨胀或收缩的球体)或旋转对称(像旋转的圆盘或球体)。这个原理的一个简单例子是旋转的哑铃。如果哑铃绕着其轴旋转,它就不会辐射引力波;如果它翻滚着旋转,就像两颗行星互相绕行的例子中那样,那么它就会辐射出引力波。哑铃越重,翻滚越快,它发出的引力辐射就越强。在极端情况下,例如当哑铃的两个重物是像中子星或黑洞那样的大质量天体,两者快速地相互绕行时,则会发出大量的引力辐射。
以下是一些更详细的例子:
- 两个互相环绕的物体会发出辐射,就像一颗行星环绕太阳那样。
- 旋转的非轴对称小行星会发出辐射,比方说在赤道上有一个大的凸起或凹痕的小行星。
- 超新星会发出辐射,除非爆炸是完全对称的。
- 以恒定速度移动的孤立的非旋转固体物体不会发出辐射。这可以看作是线性动量守恒原理的结果。
- 旋转的圆盘不会发出辐射。这可以看作是角动量守恒原理的结果。然而,它会显示出重力磁效应。
- 球形脉动球状恒星(拥有非零单极矩或质量,但四极矩为零)不会发出辐射,这符合伯克霍夫定理。
更准确地说,孤立系统的能动张量的四极矩的二阶时间导数(或第 I 个多极矩的 I 阶时间导数)必须非零才能发出引力辐射。这类似于电荷或电流的变化的偶极矩是发射电磁辐射所必需的。
4.1 双星系统
引力波将能量从它们的波源带走。在物体沿轨道转动的情况下,引力波所带来的能量损失伴随着轨道的螺旋式向内。[29][30] 例如,想象一个简单的两个质量的系统(例如地球-太阳系统),与圆形轨道上以小于光速的速率运动。假设这两个质量在 $x-y$ 平面的圆轨道上相互绕轨道运行。在很高的近似程度上,质量遵循简单的开普勒轨道。然而,这样的轨道有变化着的四极矩。也就是说,这个系统会辐射出引力波。
理论上,引力辐射造成的能量损失最终会使地球落入太阳。然而,地球绕太阳运行的总能量(动能+引力势能)约为 $ 1.14\times10^{36}$ 焦耳,其中引力辐射引起的能量损失功率只有 200 瓦(即焦耳每秒),这导致轨道每天衰减约 $ 1\times10^{-15}$ 米(大约相当于质子的直径)。按照这种速度,地球大约需要比现在的宇宙年龄多 $ 1\times10^{13}$ 倍的时间才能坠入太阳。这个估计忽略了 r 随时间的减少,但是在大多数时候天体相距很远而且只是缓慢地辐射引力波,所以在这个例子中忽略 r 随时间的减少所导致的差别并不重要。[来源请求]
更一般地,轨道衰减的速率可以被近似为[31]
其中 $r$ 是天体之间的距离,$t$ 是时间,$G$) 为引力常数,$c$ 是真空光速,$m_1$ 和 $m_2$ 分别是两个天体的质量。这可以导出预计的合并所需时间
致密双星系统
白矮星和中子星等致密的恒星可以成为双星系统的组成部分。例如,一对拥有太阳质量的中子星在圆形轨道上运行,两者相距 $ 1.89\times(10^8)$ 米(即 189,000 千米),轨道周期为 1000 秒,预期寿命为 $ 1.30\times10^{13}$ 秒(大约 414,000 年)。激光干涉仪空间天线可以观察到距我们不太远的这样的双星系统。轨道周期在这个范围内的白矮星双星系统的数量要多得多。白矮星双星的质量与太阳接近,直径与地球接近。在它们合并和爆炸成为超新星之前它们不可能靠得比 10,000 公里更近,超新星爆发也将结束引力波的发射。在此之前,它们的引力辐射可与中子星双星系统相当。
当中子星双星的轨道衰减到 $1.89\times(10^6)$ 米(即 1890 公里)时,其剩余寿命约为 130,000 秒(即 36 小时)。轨道频率将从开始时的每秒 1 个周期变化到轨道收缩到 20 公里时的每秒 918 个周期。发射的大部分引力辐射将是轨道频率的两倍。在合并之前,如果这样的双星系统离我们足够近,激光干涉引力波天文台就可以观察到这种螺旋运动。在可能长达数十亿年的整个轨道寿命中,激光干涉引力波天文台只有几分钟的时间来观察这次合并。在 2017 年 8 月,激光干涉引力波天文台和处女座干涉仪在 GW170817 事件中观测到第一例中子星双星螺旋,70 个天文台合作探测到电磁对应物,NGC 4993 星系中的一颗距我们 40 兆秒差距的千新星在合并几秒钟后发生短暂的伽玛射线爆发(GRB 170817A),随后是由 R-过程核提供能量的更长的光学瞬变(AT 2017gfo)。增进激光干涉引力波天文台探测器应该能够探测到在 200 兆秒差距之外发生的这类事件。在这个数量级的范围内我们预计每年有 40 次此类事件发生。[32]
4.2 黑洞双星
黑洞双星在螺旋、合并和衰荡阶段发射引力波。最大振幅的发射发生在合并阶段,这可以用数值相对论技术来模拟。[33][34][35] 第一次被直接探测到的引力波(GW150914)就来自于两个黑洞的合并。
4.3 超新星
超新星是一种短暂的天文事件,发生在大质量恒星生命的最后恒星演化阶段,其戏剧性和灾难性的毁灭以最终的激烈爆炸为标志。这种爆炸可能以多种方式发生,但在所有这些方式中,恒星中的大部分物质都以极高的速度(高达光速的 10%)被吹入周围的空间。除非这些爆炸拥有完美的球形对称性(即除非物质在所有方向均匀喷出),否则将会有来自爆炸的引力辐射。这是因为引力波是由变化的四极矩产生的,后者只有当质量进行不对称运动时才会发生。由于超新星爆发的确切机制还没有被完全了解,因此要模拟它们发出的引力辐射并不容易。
4.4 自转的中子星
如上所述,只有当质量之间存在不带有球对称性的运动时,质量分布才会发出引力辐射。自转的中子星一般不会发出引力辐射,因为中子星是高度致密的物体,拥有强大的引力场,这种强引力场使它们几乎保持完美的球形。然而,在某些情况下,中子星表面上可能会存在被称为 “山” 的轻微的变形,这些隆起在表面上延伸不超过 10 厘米(约 4 英寸),[36] 隆起的存在摧毁了球对称性。这使得中子星拥有一个随时间变化的四极矩并发射引力波,直到畸形被抹平。
4.5 暴胀
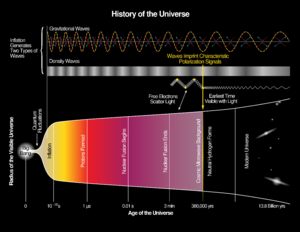
许多宇宙模型表明在宇宙早期历史中有一个暴胀时期,当时空间在很短的时间内膨胀了很多倍。如果这种膨胀不是关于所有方向都对称的,它可能已经发出了今天可以检测到的引力辐射,这被称为引力波背景。这个背景信号太弱,任何目前正在运行的引力波探测器都无法观测到它,人们认为要进行这样的观测可能还需要几十年的时间。
5. 性质和行为
5.1 能量、动量和角动量
水波、声波和电磁波能够携带能量、动量和角动量,并将能量、动量和角动量从波源带走。引力波也有同样的功能。因此,举例来说,一个双星系统会随着彼此互相螺旋靠近而失去角动量——角动量会被引力波辐射掉。
这些波还可以携带线性动量,这种可能性对天体物理学有一些有趣的影响。[37] 两个超大质量黑洞合并后,线性动量的发射会产生一个幅度高达 4000 千米每秒的 “反冲”,这足以将合并后的黑洞从宿主星系中完全弹出。即使反冲太小而不能将黑洞完全弹出,它也可以暂时将黑洞从星系核中移除,之后它将围绕中心振荡直至最终停止。[38] 被反弹的黑洞也可以携带着星团,形成一个超致密的恒星系统。[39] 或者它也可能携带气体,允许反冲的黑洞暂时表现为一个 “裸类星体”。类星体 SDSS J092712.65+294344.0 被认为包含一个反冲超大质量黑洞。[40]
5.2 红移
就像电磁波一样,引力波会由于波源和观测者的相对速度以及由于时空的变形(例如宇宙膨胀)而改变波长。即使引力本身是时空变形的原因,情况也是如此。注意,引力波的红移不同于引力引起的红移。
5.3 量子引力、波粒方面和引力子
在量子场论的框架下,引力子是一个假设的基本粒子的名字,它被推测为传递引力的载体。然而,引力子还没有被证明存在,暂时也还没有科学模型能够成功地调和描述引力的广义相对论和描述所有其他基本力的标准模型。物理学家们已经进行了一些尝试,如量子引力,但尚未被普遍接受。
如果这样的粒子存在,它被认为是无质量的(因为引力似乎有无限大的作用范围),并且必须是自旋为 2 的玻色子。可以证明,任何无质量的自旋为 2 的场都会产生一种与引力无法区分的力,因为无质量的自旋为 2 的场必须像引力场那样与能动张量相耦合(发生相互作用);因此,如果一个无质量的自旋为 2 的粒子被发现,在与其他无质量的自旋为 2 的粒子没有区别的情况下它很可能就是引力子。[41] 这样的发现将把量子理论和引力结合起来。[42]
5.4 对研究早期宇宙的意义
由于重力与物质的耦合很弱,引力波即使传播了天文距离也几乎不会被吸收或散射。特别是,引力波预计不会受到非常早期宇宙的不透明性的影响。在这些早期阶段,空间还没有变得 “透明”,所以基于来自很久远的时间之前的光、无线电波和其他电磁辐射的观测是受限的,或根本不可用。因此,引力波原则上有望为我们提供关于非常早期宇宙的大量观测数据。
5.5 确定运动方向
直接探测引力波的困难意味着单个探测器也很难自行识别波源的方向。因此,多个检测器被用于通过确认信号不是来自地球来区分信号和其他 “噪声”,同时也通过三角测量来确定波源方向。这种技术利用了这样一个事实,即引力波以光速传播,它到达不同的探测器的具体时间取决于波源的方向。虽然到达时间的差异可能只有几毫秒,但这已经足以相当精确地确定波的起源方向。
只有在 GW170814 的案例中,三个探测器才在事件发生时运行,因此这个引力波事件的波源方向被精确确定。所有三个仪器的检测都导致了对源位置的非常精确的估计,90% 的可信区域仅为 60°$^{2}$,这比以前精确了 20 倍。[43]
6. 引力波天文学
在过去的一个世纪里,天文学因使用了新的方法观察宇宙而发生了革命性的变化。天文观测最初利用的是可见光。伽利略·伽利雷率先使用望远镜来改善这些观测。然而,可见光只是电磁波谱中的一小部分,并不是遥远宇宙中的所有物体都在这一特定波段强烈发光。更多有用的信息可以在例如无线电波中找到。天文学家使用射电望远镜发现了脉冲星、类星体,并对科学家以前不知道的物体做出了其他前所未有的发现。在微波波段的观测使我们探测到了大爆炸留下的微弱印记,斯蒂芬·霍金称这一发现为 “本世纪最伟大的发现,如果不是有史以来最伟大的话”。使用伽马射线、X 射线、紫外线和红外线进行观测所得到的类似进展也给天文学带来了新的见解。随着这些光谱区域每一个都被开启,科学家们得到了一些以前难以实现的新的发现。天文学家希望引力波也是如此。[44]
引力波有两个重要而独特的性质。首先,由不带电荷的黑洞组成的双星系统产生引力波并不需要在其附近存在任何类型的物质,这样的双星系统不会发出电磁辐射。其次,引力波可以穿过任何位于其行进路线上的物质而不会被显著散射。举例来说,来自遥远恒星的光可能被星际尘埃阻挡,而引力波将基本不受阻碍地通过。这两个特征使得引力波能够携带一些迄今为止人类从未观察到的关于天文现象的信息。[45]
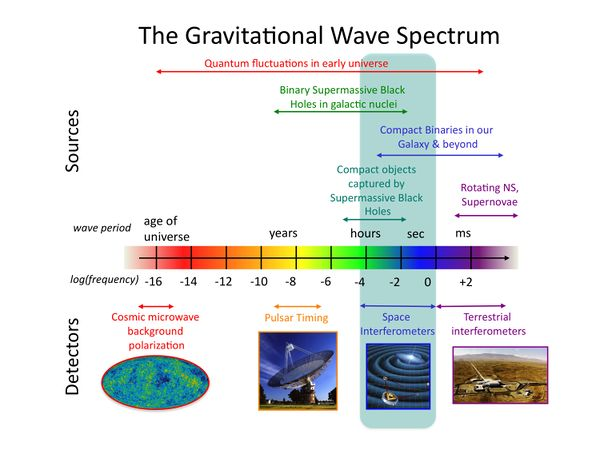
上述引力波的来源位于引力波频谱的低频端($10^{-7}$ 到 $10^{5}$ 赫兹)。引力波频谱高频端的天体物理源(高于 $10^{5}$ 赫兹,可能达到 $10^{10}$ 赫兹)生成[需要解释] 理论上被认为是大爆炸微弱印记的残余引力波,这就像宇宙微波背景。[46] 在这些高频下,波源可能可以是 “人造的”[47],也就是说,引力波可以在实验室中被生成和探测。[47][48]
一个由被哈勃空间望远镜探测到的两个合并星系中心的黑洞合并而成的超大质量黑洞理论上被认为已经被引力波从合并中心弹出。[49][50]
7. 探测
7.1 间接探测
虽然来自地球-太阳系统的波是微乎其微的,天文学家可以指出其他能够发出大量辐射的波源。一个重要的例子是赫尔斯-泰勒双星,这是一对星体,其中一个是脉冲星。[51] 它们的轨道特征可以从脉冲星发出的无线电信号的多普勒频移推断出来。这个双星系统中的每个星体的质量都约为 1.4 M☉,它们的轨道尺寸大约是地球-太阳轨道尺寸的 1/75,这个尺寸比我们太阳的直径大几倍。更大的质量和更小的距离意味着赫尔斯-泰勒双星释放的能量将远远大于地球-太阳系统释放的能量,前者约为后者的 $10^{22}$ 倍。
关于轨道的信息可以用来预测有多少能量(和角动量)将以引力波的形式被辐射出来。随着双星系统失去能量,两个星体逐渐靠近彼此,轨道周期减小。每颗恒星最终的轨道都是螺旋的,且半径逐渐减小。广义相对论精确地描述了这些轨迹;特别地,引力波辐射的能量决定了周期的下降率,这里周期被定义为连续的近星点(两颗星最接近的点)之间的时间间隔。对于赫尔斯-泰勒脉冲星,当下半径变化的预测值约为每圈轨道 3 毫米,在 7.75 小时的周期中每年的变化大约是 2 秒。在初步观察表明轨道能量损失与引力波一致后,[52] Taylor 和 Joel Weisberg 仔细的定时观察戏剧性地证实了预测的周期减少到 10% 以内。[52] 自从脉冲星被发现以来,通过对 30 多年的定时数据的改进统计,目前观测到的轨道周期变化与来自广义相对论所假设的引力辐射的预测在 0.2% 的误差内相符。[53] 1993 年,部分由于对引力波的间接探测,诺贝尔委员会将诺贝尔物理学奖授予 Hulse 和 Taylor,以表彰他们 “发现了一种新型的脉冲星,这一发现为研究引力开辟了新的可能性。”[54] 从现在到合并,这个双星系统的寿命估计为几亿年。[55]
在螺旋轨道上运动的双星系统是非常重要的引力波来源。每当两个致密天体(白矮星、中子星或黑洞)在互相非常靠近的轨道上时,它们会发出强烈的引力波。随着它们螺旋地相互靠近,这些引力波变得更加强烈。在某个时刻,它们应该变得如此强烈以至于通过它们对地球或太空中的物体的影响来对它们进行直接探测是可能的。这种直接检测是几个大尺度实验的目标。[56]
唯一的困难是大多数像赫尔斯-泰勒双星这样的系统都离我们很远。赫尔斯-泰勒双星发出的引力波在地球上的振幅大约是 $h\approx 10^{-26}$。然而,存在另外一些引力波源,天体物理学家期望它们可以产生更大振幅的引力波 $(h \approx 10^{20})$。至少有另外八个脉冲星双星系统已经被发现了。[57]
7.2 困难
引力波不容易被探测到。当它们到达地球时,它们的振幅很小,应变接近 $10^{-21}$ 这意味着需要一个极其灵敏的检测器,并且其他噪声源可能会淹没信号。[58] 引力波的频率预计为 $10^{16}$ 赫兹 < $f$ < $10^{4}$ 赫兹。[59]
7.3 地面探测器
尽管赫尔斯-泰勒的观察非常重要,但他们只给出引力波存在的间接证据。更确切的观察是直接测量引力波通过的效果,这也可以提供更多关于产生引力波的系统的信息。任何这样的直接探测都是复杂的,因为波对探测器所产生的影响可能会非常小。球面波的振幅将随着与波源的距离的倒数(上面关于 h 的式子中的 1/R 项)而减弱。因此,即使是来自极端系统的波,如合并的双黑洞,在到达地球时也会减弱到非常小的振幅。天体物理学家预计一些穿过地球的引力波可能有 $(h \approx 10^{-20})$,但一般不会更大。[60]
共振天线
一种理论上用来探测预期的引力波运动的简单设备叫做韦伯棒,它是一个与外界振动隔绝的巨大实心金属棒。这类仪器是第一类引力波探测器。被入射引力波引起的空间应变激发了棒的共振频率,因此可以被放大到可检测的水平。可以想象,附近的超新星可能足够强大以致可以在没有共振放大的情况下被看见。Joseph Weber 声称用这台仪器检测到了引力波的日常信号。然而,他的结果在 1974 年受到物理学家 Richard Garwin 和 David Douglass 的质疑。现代形式的韦伯棒仍然在运行,它们被低温冷却,用超导量子干涉设备来检测振动。韦伯棒不够灵敏,除了极其强大的引力波之外,什么也探测不到。[61]
MiniGRAIL 是一种使用这一原理的球形引力波天线。它位于莱顿大学,是一个精密加工的 1150 千克球体,这个球体被低温冷却至 20 毫开尔文。[62] 球形结构允许在所有方向上具有相等的灵敏度,并且在实验上比需要高度真空的较大线性装置简单一些。物理学家通过测量探测器球体的变形来探测引力波事件。MiniGRAIL 在 2-4 千赫兹的范围内非常敏感,适用于探测来自旋转中子星不稳定性或小型黑洞合并的引力波。[63]
目前有两个探测器聚焦在引力波频谱的高频端($10^{-7}$ 到 $10^5$ 赫兹):一个在英国伯明翰大学,另一个在意大利热那亚的 INFN。第三个正被建造于中国重庆大学。伯明翰探测器测量在一米宽的闭环中循环的微波束的偏振状态的变化。预计这两种探测器对 $h \sim 2\times 10^{-13} /\sqrt{\text{Hz}}$ 的周期性时空应变都很敏感,给定为振幅谱密度。INFN 热那亚探测器是一个共振天线,由两个直径几厘米的耦合球形超导谐振子组成。振荡器被设计成(未耦合时)具有几乎相等的共振频率。该系统目前预计对 $h \sim 2 \times 10^{-17} /\sqrt{\text{Hz}}$ 的周期性时空应变具有敏感性,并期望达到 $h \sim 2 \times 10^{-20} /\sqrt{\text{Hz}}$ 的灵敏度。重庆大学探测器计划探测的共振参数约为 $10^{11}$ 赫兹(100 GHz)和 $h \sim 10^{-30}$ 到 $10^{-32}$ 的残余高频引力波。
干涉仪
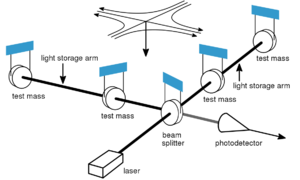
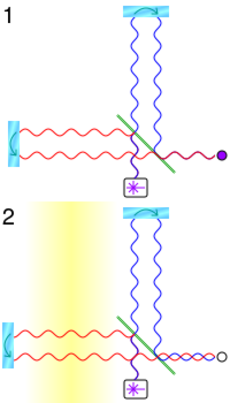
一类更敏感的探测器使用激光干涉测量法来测量分离的 “自由” 质量之间由引力波引起的运动。[66] 这允许质量被大距离分开(增加信号大小);另一个优点是它对很宽的频率范围敏感(不仅仅是那些接近共振的频率,就像韦伯棒)。经过多年的发展,第一台地基干涉仪于 2015 年投入使用。目前,最敏感的是 LIGO,即激光干涉引力波天文台。激光干涉引力波天文台有三个探测器:一个在路易斯安那州的 Livingston,一个在华盛顿州 Richland 的 Hanford 区,第三个(以前作为第二个探测器安装在 Hanford)计划转移到印度。每个天文台都有两个 4 公里长的光存储臂。它们互相之间成 90 度夹角,光在贯穿整个 4 公里的直径为 1 米的真空管中穿过。经过的引力波会稍微拉伸其中一个光储存臂,同时缩短另一个。这正是干涉仪最敏感的运动。
即使有这么长的臂,最强的引力波也只能使光储存臂末端之间的距离改变最多大约 $10^{-18}$ 米。激光干涉引力波天文台应该能够探测到小到 $h \sim 5 \times 10^{22}$ 的引力波。激光干涉引力波天文台和处女座干涉仪的升级将会进一步提高灵敏度。另一个高灵敏度的干涉仪,KAGRA,正在日本的神冈矿建设中。一个关键点是灵敏度(“到达” 半径)增加 10 倍会使仪器的可用空间的体积增加 1000 倍。这将可检测信号的出现率从每数十年一次提高到每年几十次。[67]
干涉探测器在高频受到散粒噪声的限制,散粒噪声的出现是因为激光随机产生光子;一个类比是降雨:降雨的速率(像激光的强度)是可以测量的,但是雨滴(像光子)会随机的落下,造成在平均值附近的波动。这导致探测器输出端产生噪声,很像无线电静电。此外,对于足够高的激光功率,由激光光子传递到测试质量的随机动量会使得反射镜发生震动,掩盖低频信号。热噪声(例如布朗运动)是对灵敏度的另一个限制。除了这些 “稳定”(恒定)噪声源之外,所有地基探测器在低频也受到地震噪声和其他形式的环境振动以及其他 “非稳定” 噪声源的限制;机械结构的嘎吱声、闪电或其他大的电气干扰等也可能产生掩盖事件的噪声,甚至可能模拟事件。在探测结果被认定为真正的引力波事件之前,所有这些因素必须在分析中被考虑和排除。
Einstein@Home
最简单的引力波是频率恒定的引力波。旋转的非轴对称中子星发出的引力波近似是单色的:声学中的纯音。与来自超新星或黑洞双星的信号不同,这些信号在被地面探测器观测到的时间内,其振幅或频率几乎没有变化。然而,由于地球运动引起的多普勒频移,测量到的信号会有一些变化。尽管信号很简单,但由于需要分析的数据量很大,探测的计算成本非常高。
Einstein@Home 项目是一个类似 SETI@home 的分布式计算项目,旨在探测这种引力波。通过从 LIGO 和 GEO 获取数据,并以小块的形式发送给成千上万的志愿者,让他们在家用电脑上进行并行分析,Einstein@Home 可以比其他方式更快地进行数据筛选。[68]
7.4 天基干涉仪
天基干涉仪也正在开发中,例如激光干涉空间天线(LISA)和分赫兹干涉引力波天文台(DECIGO)。LISA 的设计要求三个测试质量形成等边三角形,每个航天器的激光器互相形成两个独立的干涉仪。LISA 计划占据一个跟踪地球的太阳轨道,三角形的每条边长 500 万公里。这将探测器置于远离地球噪声源的良好真空中,尽管它仍然容易受到热量、散粒噪声以及宇宙射线和太阳风所造成的人为因素的影响。
7.5 使用脉冲星计时阵列
脉冲星是快速旋转的恒星。脉冲星发射无线电波束,就像灯塔的光束一样,随着脉冲星的旋转扫过天空。来自脉冲星的信号可以被射电望远镜检测为一系列有规则间隔的脉冲,非常像时钟的滴答声。引力波影响了脉冲从脉冲星传播到地球上的望远镜所需的时间。脉冲星计时阵列使用毫秒脉冲星在测量脉冲到达望远镜的时间时寻找来自引力波的扰动,换句话说,寻找时钟周期的偏差。为了探测引力波,脉冲星计时阵列寻找来自几个脉冲星的脉冲到达时间之间不同的相关和负相关模式。[69] 虽然脉冲星的脉冲在太空中传播数百年或数千年才到达我们这里,但脉冲星计时阵列对其传播时间远小于百万分之一秒的扰动非常敏感。
脉冲星计时阵列所敏感的引力波的主要来源是由星系碰撞所形成的超大质量黑洞双星。[70] 除了单独的双星系统,脉冲星计时阵列也对来自许多合并星系的引力波总和的引力波随机背景敏感。其他潜在的信号源包括宇宙弦以及来自宇宙暴胀的引力波原初背景。
全球有三个活跃的脉冲星计时阵列项目。北美纳赫兹引力波天文台使用阿雷西博天文台和格林班克望远镜所收集的数据。澳大利亚帕克斯脉冲星计时阵列使用来自帕克斯射电望远镜的数据。欧洲脉冲星计时阵列使用欧洲四个最大望远镜的数据,它们分别是:洛弗尔望远镜、韦斯特博克合成射电望远镜、埃弗斯伯格望远镜和南凯射电望远镜。这三个小组还以国际脉冲星计时阵列项目的名义开展合作。[71]
7.6 原初引力波
原初引力波是在宇宙微波背景中观测到的引力波。据称,它们曾被 BICEP2 仪器探测到,相关公告发布于 2014 年 3 月 17 日,并于 2015 年 1 月 30 日被撤回。(“该信号可完全归因于银河系中的灰尘”)[72]
7.7 激光干涉引力波天文台和处女座干涉仪的观测
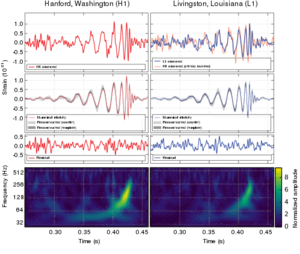
2016 年 2 月 11 日,激光干涉引力波天文台合作组织宣布从格林尼治时间 2015 年 9 月 14 日 09:50:45 检测到的信号中首次观测到引力波,[73] 这次的引力波来自于约 13 亿光年外的两个质量分别为 29 倍和 36 倍太阳质量的黑洞的合并。在合并的最后一刻,它释放的能量的功率是可观测宇宙中所有恒星总和的 50 倍以上。[74] 信号在 10 个周期(5 个轨道)内频率从 35 赫兹增加到 250 赫兹,同时它的强度在 0.2 秒内增加了。[75] 合并产生的黑洞的质量是 62 倍太阳质量。相当于 3 倍太阳质量的能量以引力波的形式发出。[75] Livingston 和 Hanford 的两个激光干涉引力波天文台探测器都看到了这个信号,由于两个探测器和光源之间的角度,两个探测器接收到引力波信号的时间差为 7 毫秒。信号来自南天球,方向大致是麦哲伦云方向(但要比麦哲伦云远得多)。[76] 这次对引力波的观测的置信度为 99.99994%。[75]
从那以后,激光干涉引力波天文台和处女座干涉仪报告了更多来自合并黑洞双星的引力波观测。
2017 年 10 月 16 日,激光干涉引力波天文台和处女座干涉仪合作组织宣布首次探测到源自中子星双星系统合并的引力波。对发生在 2017 年 8 月 17 日的编号为 GW170817 的短暂事件的观测使得我们能够将涉及的中子星的质量限制在 0.86 倍至 2.26 倍太阳质量之间。更进一步的分析将质量值更精确地限制在 1.17-1.60 倍太阳质量的区间,测量的双星系统总质量为 2.73-2.78 倍太阳质量。处女座探测器的加入使得对波源的定位提高了 10 倍。这反过来又促进了对引力波事件的电磁跟踪。与双黑洞合并的情况不同,双中子星合并预期会产生电磁对应物,即与事件相关的光信号。费米伽玛射线空间望远镜探测到一次伽玛射线爆发(GRB 170817A),发生在引力波瞬变 1.7 秒后。这个信号来自 NGC 4993 星系附近,与中子星合并有关。该事件的电磁跟踪(AT 2017gfo)证实了这一点,这涉及 70 个望远镜和天文台,并得到了对大范围电磁频谱的观测结果,后者进一步证实了合并天体和相关千新星的中子星本质。[76][76]
8. 8 在小说中
由 Arkady 和 Boris Strugatsky 两兄弟所写的俄罗斯科幻小说《Space Apprentice》中的一集就展示了以摧毁小行星 15 Eunomia 上一块珠穆朗玛峰大小的碎片为代价来监测引力波传播的实验。[77]
在 Stanislaw Lem 的小说《Fiasco》中,一把 “重力枪” 或 “渐变器”(通过共振的准直发射进行重力放大)来重塑坍缩星,以便主角可以利用极端相对论效应并进行星际旅程。
在 Greg Egan 的小说《Diaspora》中,对来自附近的中子星双星系统的螺旋轨道的引力波信号的分析表明,它的碰撞和合并即将来临,这意味着一次大型伽马射线爆发将冲击地球。
在刘慈欣的《三体》系列中,引力波被用作星际广播信号,是星系内文明冲突的中心情节点。
9. 参考文献
- https://web.archive.org/web/20221028205210/http://www.academie-sciences.fr/pdf/dossiers/Poincare/Poincare_pdf/Poincare_CR1905.pdf.
- Einstein, A (June 1916). "Näherungsweise Integration der Feldgleichungen der Gravitation". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. part 1: 688–696. Bibcode:1916SPAW.......688E..
- Finley, Dave. "Einstein's gravity theory passes toughest test yet: Bizarre binary star system pushes study of relativity to new limits". Phys.Org..
- The Detection of Gravitational Waves using LIGO, B. Barish Archived 2016-03-03 at the Wayback Machine.
- Einstein, Albert; Rosen, Nathan (January 1937). "On gravitational waves". Journal of the Franklin Institute. 223 (1): 43–54. Bibcode:1937FrInJ.223...43E. doi:10.1016/S0016-0032(37)90583-0..
- Nobel Prize Award (1993) Press Release The Royal Swedish Academy of Sciences..
- LIGO Scientific Collaboration and Virgo Collaboration (2016). "GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence". Physical Review Letters. 116 (24): 241103. arXiv:1606.04855. Bibcode:2016PhRvL.116x1103A. doi:10.1103/PhysRevLett.116.241103. PMID 27367379..
- Abbott, B. P; Abbott, R; Abbott, T. D; Acernese, F; Ackley, K; Adams, C; Adams, T; Addesso, P; Adhikari, R. X; Adya, V. B; Affeldt, C; Afrough, M; Agarwal, B; Agathos, M; Agatsuma, K; Aggarwal, N; Aguiar, O. D; Aiello, L; Ain, A; Ajith, P; Allen, B; Allen, G; Allocca, A; Altin, P. A; Amato, A; Ananyeva, A; Anderson, S. B; Anderson, W. G; Antier, S; et al. (2017). "GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2". Physical Review Letters (in 英语). 118 (22): 221101. arXiv:1706.01812. Bibcode:2017PhRvL.118v1101A. doi:10.1103/physrevlett.118.221101. PMID 28621973..
- "European detector spots its first gravitational wave". 27 September 2017. Retrieved 27 September 2017..
- "The Newest Search for Gravitational Waves has Begun". LIGO Caltech. LIGO. 18 September 2015. Retrieved 29 November 2015..
- "First Second of the Big Bang". How The Universe Works 3. 2014. Discovery Science..
- Bernard Schutz (14 May 2009). A First Course in General Relativity. Cambridge University Press. ISBN 978-0-521-88705-2..
- LIGO Scientific Collaboration; Virgo Collaboration (2012). "Search for Gravitational Waves from Low Mass Compact Binary Coalescence in LIGO's Sixth Science Run and Virgo's Science Runs 2 and 3". Physical Review D. 85 (8): 082002. arXiv:1111.7314. Bibcode:2012PhRvD..85h2002A. doi:10.1103/PhysRevD.85.082002..
- Krauss, LM; Dodelson, S; Meyer, S (2010). "Primordial Gravitational Waves and Cosmology". Science. 328 (5981): 989–992. arXiv:1004.2504. Bibcode:2010Sci...328..989K. doi:10.1126/science.1179541. PMID 20489015..
- Heaviside O. A gravitational and electromagnetic analogy,Electromagnetic Theory, 1893, vol.1 455–466 Appendix B.
- (PDF) Membres de l'Académie des sciences depuis sa création : Henri Poincare. Sur la dynamique de l' electron. Note de H. Poincaré. C.R. T.140 (1905) 1504–1508..
- "page 1507" (PDF)..
- Cervantes-Cota, J.L.; Galindo-Uribarri, S.; Smoot, G.F. (2016). "A Brief History of Gravitational Waves". Universe. 2 (3): 22. arXiv:1609.09400. Bibcode:2016Univ....2...22C. doi:10.3390/universe2030022..
- Daniel Kennefick (29 March 2016). Traveling at the Speed of Thought: Einstein and the Quest for Gravitational Waves. Princeton University Press. ISBN 978-1-4008-8274-8..
- Taylor, J.; Weisberg, J.M. (1979). "A New Test of General Relativity: Gravitational Radiation and the Binary Pulsar PSR 1913+16". Astrophysical Journal. 253 (5696): 908–920. Bibcode:1979Natur.277..437T. doi:10.1038/277437a0..
- Gertsenshtein, M. E.; Pustovoit, V. I. (1962). "On the detection of low frequency gravitational waves". JETP. 43: 605–607..
- Cho, Adrian (Oct. 3, 2017). "Ripples in space: U.S. trio wins physics Nobel for discovery of gravitational waves," Science. Retrieved 20 May 2019..
- Cervantes-Cota, Jorge L., Galindo-Uribarri, Salvador, and Smoot, George F. (2016). "A Brief History of Gravitational Waves," Universe, 2, no. 3, 22. Retrieved 20 May 2019..
- "Gravitational waves detected 100 years after Einstein's prediction | NSF - National Science Foundation". www.nsf.gov. Retrieved 2016-02-11..
- Ian Sample. "Gravitational waves turn to dust after claims of flawed analysis". the Guardian..
- Rincon, Paul; Amos, Jonathan (3 October 2017). "Einstein's waves win Nobel Prize". BBC News. Retrieved 3 October 2017..
- Landau, L. D.; Lifshitz, E. M. (1975). The Classical Theory of Fields (Fourth Revised English ed.). Pergamon Press. pp. 356–357. ISBN 978-0-08-025072-4..
- Einstein, A (1918). "Über Gravitationswellen". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. part 1: 154–167. Bibcode:1918SPAW.......154E..
- Peters, P.; Mathews, J. (1963). "Gravitational Radiation from Point Masses in a Keplerian Orbit". Physical Review. 131 (1): 435–440. Bibcode:1963PhRv..131..435P. doi:10.1103/PhysRev.131.435..
- Peters, P. (1964). "Gravitational Radiation and the Motion of Two Point Masses" (PDF). Physical Review. 136 (4B): B1224–B1232. Bibcode:1964PhRv..136.1224P. doi:10.1103/PhysRev.136.B1224..
- "Wayback Machine" (PDF). 29 January 2016..
- LIGO Scientific Collaboration – FAQ; section: "Do we expect LIGO's advanced detectors to make a discovery, then?" and "What's so different about LIGO's advanced detectors?", retrieved 14 February 2016.
- Pretorius, Frans (2005). "Evolution of Binary Black-Hole Spacetimes". Physical Review Letters. 95 (12): 121101. arXiv:gr-qc/0507014. Bibcode:2005PhRvL..95l1101P. doi:10.1103/PhysRevLett.95.121101. ISSN 0031-9007. PMID 16197061..
- Campanelli, M.; Lousto, C. O.; Marronetti, P.; Zlochower, Y. (2006). "Accurate Evolutions of Orbiting Black-Hole Binaries without Excision". Physical Review Letters. 96 (11): 111101. arXiv:gr-qc/0511048. Bibcode:2006PhRvL..96k1101C. doi:10.1103/PhysRevLett.96.111101. ISSN 0031-9007. PMID 16605808..
- Baker, John G.; Centrella, Joan; Choi, Dae-Il; Koppitz, Michael; van Meter, James (2006). "Gravitational-Wave Extraction from an Inspiraling Configuration of Merging Black Holes". Physical Review Letters. 96 (11): 111102. arXiv:gr-qc/0511103. Bibcode:2006PhRvL..96k1102B. doi:10.1103/PhysRevLett.96.111102. ISSN 0031-9007. PMID 16605809..
- "Neutron Star Crust Is Stronger than Steel". Retrieved 2016-07-01..
- Merritt, D.; et al. (May 2004). "Consequences of Gravitational Wave Recoil". The Astrophysical Journal Letters. 607 (1): L9–L12. arXiv:astro-ph/0402057. Bibcode:2004ApJ...607L...9M. doi:10.1086/421551..
- Gualandris A, Merritt D, et al. (May 2008). "Ejection of Supermassive Black Holes from Galaxy Cores". The Astrophysical Journal. 678 (2): 780–797. arXiv:0708.0771. Bibcode:2008ApJ...678..780G. doi:10.1086/586877..
- Merritt, D.; Schnittman, J. D.; Komossa, S. (2009). "Hypercompact Stellar Systems Around Recoiling Supermassive Black Holes". The Astrophysical Journal. 699 (2): 1690–1710. arXiv:0809.5046. Bibcode:2009ApJ...699.1690M. doi:10.1088/0004-637X/699/2/1690..
- Komossa, S.; Zhou, H.; Lu, H. (May 2008). "A Recoiling Supermassive Black Hole in the Quasar SDSS J092712.65+294344.0?". The Astrophysical Journal. 678 (2): L81–L84. arXiv:0804.4585. Bibcode:2008ApJ...678L..81K. doi:10.1086/588656..
- For a comparison of the geometric derivation and the (non-geometric) spin-2 field derivation of general relativity, refer to box 18.1 (and also 17.2.5) of Misner, C. W.; Thorne, K. S.; Wheeler, J. A. (1973). Gravitation. W. H. Freeman. ISBN 978-0-7167-0344-0..
- Lightman, A. P.; Press, W. H.; Price, R. H.; Teukolsky, S. A. (1975). "Problem 12.16". Problem book in Relativity and Gravitation. Princeton University Press. ISBN 978-0-691-08162-5..
- Update on Gravitational Wave Science from the LIGO-Virgo Scientific Collaborations (Video of the press conference), retrieved 27 September 2017.
- Berry, Christopher (14 May 2015). "Listening to the gravitational universe: what can't we see?". University of Birmingham. University of Birmingham. Retrieved 29 November 2015..
- Mack, Katie (2017-06-12). "Black Holes, Cosmic Collisions and the Rippling of Spacetime". The Atlantic..
- Grishchuk, L. P. (1976). "Primordial Gravitons and the Possibility of Their Observation". Sov. Phys. JETP Lett. 23 (6): 293–296. Bibcode:1976ZhPmR..23..326G. PACS numbers: 04.30. + x, 04.90. + e.
- Hawking, S. W.; Israel, W. (1979). General Relativity: An Einstein Centenary Survey. Cambridge: Cambridge University Press. p. 98. ISBN 978-0-521-22285-3..
- Li, Fangyu, Baker, R. M L, Jr., and Woods, R. C., "Piezoelectric-Crystal-Resonator High-Frequency Gravitational Wave Generation and Synchro-Resonance Detection", in the proceedings of Space Technology and Applications International Forum (STAIF-2006), edited by M.S. El-Genk, AIP Conference Proceedings, Melville NY 813: 2006..
- Wall, SPACE.com, Mike. "Gravitational Waves Send Supermassive Black Hole Flying". Scientific American (in 英语). Retrieved 2017-03-27..
- Chiaberge, M.; Ely, J. C.; Meyer, E. T.; Georganopoulos, M.; Marinucci, A.; Bianchi, S.; Tremblay, G. R.; Hilbert, B.; Kotyla, J. P. (2016-11-16). "The puzzling case of the radio-loud QSO 3C 186: a gravitational wave recoiling black hole in a young radio source?". Astronomy & Astrophysics. 600: A57. arXiv:1611.05501. Bibcode:2017A&A...600A..57C. doi:10.1051/0004-6361/201629522..
- The LIGO Scientific Collaboration; the Virgo Collaboration (2004). "Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis". Binary Radio Pulsars. 328: 25. arXiv:astro-ph/0407149. Bibcode:2005ASPC..328...25W..
- Taylor, J. H.; Fowler, L. A.; McCulloch, P. M. (1979). "Overall measurements of relativistic effects in the binary pulsar PSR 1913 + 16". Nature. 277: 437–440. Bibcode:1982ApJ...253..908T. doi:10.1086/159690.. [53]
- Huang, Y.; Weisberg, J. M. (2016). "Relativistic Measurements from Timing the Binary Pulsar PSR B1913+16". Astrophysical Journal. 829 (1): 55. arXiv:1606.02744. Bibcode:2016ApJ...829...55W. doi:10.3847/0004-637X/829/1/55..
- "Nobel Prizes and Laureates - NobelPrize.org". NobelPrize.org..
- Damour, Thibault (2015). "1974: the discovery of the first binary pulsar". Classical and Quantum Gravity. 32 (12): 124009. arXiv:1411.3930. Bibcode:2015CQGra..32l4009D. doi:10.1088/0264-9381/32/12/124009..
- Crashing Black Holes.
- Binary and Millisecond Pulsars Archived 2012-03-01 at the Wayback Machine.
- "Noise and Sensitivity". gwoptics: Gravitational wave E-book. University of Birmingham. Retrieved 10 December 2015..
- Thorne, Kip S. (1995). "Gravitational Waves". Particle and Nuclear Astrophysics and Cosmology in the Next Millenium: 160. arXiv:gr-qc/9506086. Bibcode:1995pnac.conf..160T..
- Blair DG, ed. (1991). The detection of gravitational waves. Cambridge University Press..
- For a review of early experiments using Weber bars, see Levine, J. (April 2004). "Early Gravity-Wave Detection Experiments, 1960–1975". Physics in Perspective. 6 (1): 42–75. Bibcode:2004PhP.....6...42L. doi:10.1007/s00016-003-0179-6..
- De Waard, A.; Gottardi, L.; Frossati, G. (2006). "MiniGRAIL, the first spherical gravitational wave detector". Recent Developments in Gravitational Physics: 415. Bibcode:2006rdgp.conf..415D..
- de Waard, Arlette; Luciano Gottardi; Giorgio Frossati (July 2000). Spherical Gravitational Wave Detectors: cooling and quality factor of a small CuAl6
%sphere. Marcel Grossmann meeting on General Relativity. Rome, Italy: World Scientific Publishing Co. Pte. Ltd. (published December 2002). pp. 1899–1901. Bibcode:2002nmgm.meet.1899D. doi:10.1142/9789812777386_0420. ISBN 9789812777386.. - Cruise, Mike. "Research Interests". Astrophysics & Space Research Group. University of Birmingham. Retrieved 29 November 2015..
- High Frequency Relic Gravitational Waves Archived 2016-02-16 at the Wayback Machine. page 12.
- The idea of using laser interferometry for gravitational wave detection was first mentioned by Gerstenstein and Pustovoit 1963 Sov. Phys.–JETP 16 433. Weber mentioned it in an unpublished laboratory notebook. Rainer Weiss first described in detail a practical solution with an analysis of realistic limitations to the technique in R. Weiss (1972). "Electromagetically Coupled Broadband Gravitational Antenna". Quarterly Progress Report, Research Laboratory of Electronics, MIT 105: 54..
- LIGO Scientific Collaboration; Virgo Collaboration (2010). "Predictions for the rates of compact binary coalescences observable by ground-based gravitational-wave detectors". Classical and Quantum Gravity. 27 (17): 17300. arXiv:1003.2480. Bibcode:2010CQGra..27q3001A. doi:10.1088/0264-9381/27/17/173001..
- "Einstein@Home"..
- Hellings, R.W.; Downs, G.S. (1983). "Upper limits on the isotropic gravitational radiation background from pulsar timing analysis". Astrophysical Journal Letters. 265: L39–L42. Bibcode:1983ApJ...265L..39H. doi:10.1086/183954..
- Arzoumanian Z, et al. (NANOGrav Collaboration) (2018). "The NANOGrav 11-year Data Set: Pulsar-timing Constraints On The Stochastic Gravitational-wave Background". The Astrophysical Journal. 859 (1): 47. arXiv:1801.02617. Bibcode:2018ApJ...859...47A. doi:10.3847/1538-4357/aabd3b..
- Hobbs, G.; et al. (2010). "The International Pulsar Timing Array project: using pulsars as a gravitational wave detector". Classical and Quantum Gravity. 27 (8): 084013. arXiv:0911.5206. Bibcode:2010CQGra..27h4013H. doi:10.1088/0264-9381/27/8/084013..
- Staff (17 March 2014). "BICEP2 2014 Results Release". National Science Foundation. Retrieved 18 March 2014..
- "Gravitational waves from black holes detected". BBC News. 11 February 2016..
- "This collision was 50 times more powerful than all the stars in the universe combined"..
- Abbott BP, et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). "Observation of Gravitational Waves from a Binary Black Hole Merger". Physical Review Letters. 116 (6): 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. doi:10.1103/PhysRevLett.116.061102. PMID 26918975..
- Castelvecchi, Davide; Witze, Witze (11 February 2016). "Einstein's gravitational waves found at last". Nature News. doi:10.1038/nature.2016.19361. Retrieved 2016-02-11..
- ME Gerstenstein; VI Pustovoit (1962). "On the Detection of Low-Frequency Gravitational Waves". ZhETF (in 俄语). 16 (8): 605–607. Bibcode:1963JETP...16..433G..