厦门大学 2000 年 考研 量子力学
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. (30 分)回答和计算下列问题
- 由费密子组成的全同粒子体系,对于交换两个费密子,体系的波函数是对称的还是反对称的?
- 什么是简并度?一维自由粒子激发态所对应的能级是几重简并?
- 定义 \[ [\hat{A}, \hat{B}] = \hat{A} \hat{B} - \hat{B} \hat{A} ~ \] 试计算 \[ [z, [\hat{L}_x, \hat{P}_y]] = ?~ \] 其中 $z, \hat{L}_x, \hat{P}_y$ 分别是坐标 $\vec r$ 的 $Z$ 分量、角动量 $\vec{L}$ 的 $X$ 分量、动量 $\vec{P}$ 的 $Y$ 分量。
- 粒子在中心力场中运动,问:$\hat P_z$ 是否守恒量?为什么?
- 什么是宇称守恒?宇称算符是厄米算符吗?为什么?
2. (20 分)
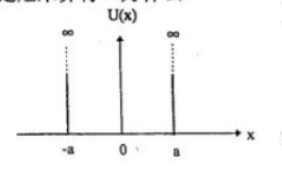
粒子在一维势场 \[U(x) = \begin{cases} 0, & |x| < a \\\\ \infty, & |x| \geq a \end{cases}~\] 中运动,如图所示:
图 1
- 求该粒子的能级和对应的归一化波函数。
- 设粒子处于第一激发态,试求动量算符 $P$ 在此态上的平均值。