波的强度

贡献者： addis; FFjet

预备知识　波的能量，流密度

　　为了描述能量随着波动的进行而在介质中传播的情况，引入能流的概念。

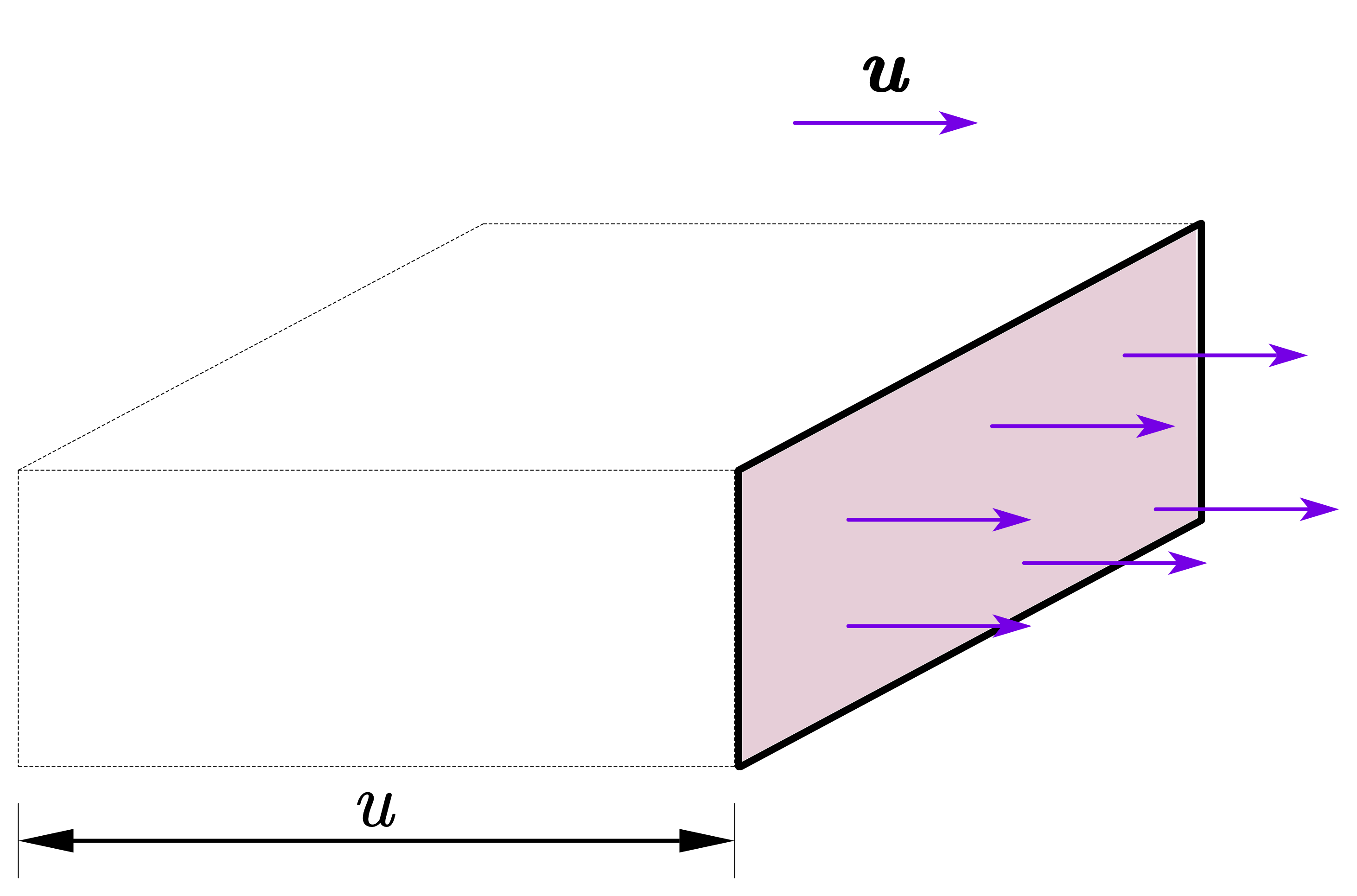
　　单位时间内通过介质中某面积的能量称为通过该面积的能流（energy flow）。设在某一介质中，垂直于波速 $u$ 的方向，取面积 $S$，则在单位时间内通过 $S$ 面的能量等于体积 $uS$ 中的能量，如图 1 所示

图 1：体积 $uS$ 内的能量在单位时间内通过 $S$ 面

　　此能量是周期性变化的，通常取其一个周期的时间平均值，得到平均能流为

\begin{equation} \overline{P}=\overline{w} u S~, \end{equation}

式中，$\overline w$ 为平均能量密度。通过与波动传播方向垂直的单位面积的平均能流，称为平均能流密度，又称波的强度（intensity of wave），用 $I$ 来表示，即

\begin{equation} I=\overline{w} u=\frac{1}{2} \rho u \omega^{2} A^{2}=\frac{1}{2} Z \omega^{2} A^{2}~, \end{equation}

其中

\begin{equation} Z=\rho u~ \end{equation}

是表征介质特性的一个常量，称为介质的特性阻抗。式 2 表明，弹性介质中简谐波的强度正比于振幅的平方，正比角频率（或频率）的平方，还正比于介质的特性阻抗。在国际单位制中，波的强度单位为 $\mathrm{W}/\mathrm{m^2}$。