万有引力（综述）

贡献者：待更新

　　（本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　牛顿的万有引力定律指出，每个粒子都会以一种与质量的乘积成正比且与它们的中心之间的距离的平方成反比的力吸引宇宙中的所有其他粒子。这是一个由艾萨克·牛顿从所谓的归纳推理经验观察中导出的一般物理定律。[1]它是经典力学的一部分，并详细地阐述在牛顿的自然哲学的数学原理 (“the Principia”) 著作之中，首次发表于 1687 年 7 月 5 日。当牛顿在 1686 年 4 月向皇家学会提交未出版文本的第一卷时，罗伯特·胡克声称牛顿从他那里获得了平方反比定律。

　　在今天的语言中，牛顿定律规定每个点的质量都受到沿与两个点相交的线的作用力吸引的其他点的质量。力与两个质量的乘积成正比，与它们之间距离的平方成反比。[2]

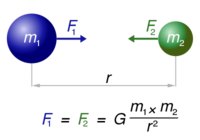
　　因此，万有引力方程的表达式为:

　　 $F = G \frac{m_1 m_2}{r^2}$

　　其中 F 是作用在两个物体之间的重力，$m_1$ 和 $m_2$ 是物体的质量，$r$ 是它们的质心之间的距离，$G$ 是重力常数。

　　 1798 年，英国科学家亨利·卡文迪许在卡文迪什实验中进行了对牛顿质量间引力理论的第一次测试。[3] 它发生在牛顿的《原理》出版 111 年后，距他去世大约 71 年。

　　牛顿的引力定律类似于电力的库仑定律，用于计算两个带电体之间产生的电力的大小。两者都是平方反比定律，其中力与物体之间距离的平方成反比。库仑定律用两个电荷的乘积代替质量的乘积，用静电常数代替重力常数。

　　虽然牛顿定律后来被阿尔伯特·爱因斯坦的广义相对论所取代，但在大多数应用中，它仍然被用作为重力效应的一个极好的近似研究。只有当需要极端的准确性时，或者当处理非常强的引力场时才需要考虑相对性的影响因素，例如在极其巨大和致密的物体附近，或者在非常近的距离(例如水星绕太阳的轨道)。

1. 历史

1.1 早期历史

　　最近，马尔迪和里奇奥利在 1640 年至 1650 年间证实了自由落体中物体的距离与所用时间之间的平方关系。他们还通过记录钟摆的振荡来计算重力常数。[4]

　　关于平方反比定律早期历史的现代评估是，“到 17 世纪 70 年代末”，关于 “重力和距离平方成反比” 的假设相当普遍，许多不同的人出于不同的原因提出了这一假设。[5]同一位作者认为罗伯特·胡克做出了重大而开创性的贡献，但是将胡克在反平方点上的优先权要求视为无关紧要，因为除了牛顿和胡克之外，还有其他几个人提出了这一点。相反，他指出 “复合天体运动” 的想法以及牛顿思想从 “离心力” 到 “向心力” 的转变是胡克的重要贡献。

　　牛顿在其《原理》中赞扬了两个人：布里亚杜斯（Bullialdus，他提出来地球有向太阳的力这一猜想）和博雷利（Borelli，他提出了所有行星都被吸引向太阳）。[6][7]对牛顿主要的影响可能来自于博雷利，他的书牛顿有一副本。[8]

1.2 剽窃争议

　　 1686 年，当第一本《牛顿原理》被提交给皇家学会时，罗伯特·胡克（Robert Hooke）指责牛顿剽窃，声称他从自己身上拿走了 “重力下降规律，即与中心距离的平方相互作用” 的 “概念”。同时(根据埃德蒙多·哈雷的当代报告)，胡克同意 “由此产生的曲线的演示” 完全是牛顿的。[9]

　　这样，就产生了牛顿欠胡克的问题，如果有的话。从那时起，这是一个广泛讨论的主题，下面概述的一些观点继续引起争议。

1.3 胡克的作品和主张

　　罗伯特·胡克在 16 世纪 60 年代发表了他关于 “世界体系” 的观点，当时他在 1666 年 3 月 21 日向英国皇家学会宣读了一篇论文 “关于通过附带的吸引原理将直接运动转变为曲线”，并在 1674 年以更为详尽拓展的形式再次发表了这些思想，作为对 “从观测中证明地球运动的尝试” 的补充。[10]胡克在 1674 年宣布，他计划 “解释一个在许多细节上不同于任何已知的世界系统”，其观点基于三个 “假设”:即 “任何天体，都有朝向自己中心的吸引力或引力”，以及 “它们也吸引在其活动范围内的所有其他天体”；[11]“所有被置于直接和简单运动的物体，将继续沿着直线前进，直到它们被其他一些有效的力偏转和弯曲……”；而且 “这些吸引人的力量远比身体靠近自己的中心要强大得多”。因此胡克清楚地假设了太阳与行星之间的相互吸引，其方式是随着与吸引体的距离增加以及线性惯性原理而增加。

　　然而，胡克直到 1674 年的声明没仍然有提到平方反比定律适用于或可能适用于这些吸引力。因此，胡克的引力理论也不是普遍的，尽管它比以前的假设更接近普遍性。[12]他也没有提供相关的证据或数学证明。关于后两个方面，胡克本人在 1674 年说过：“现在我还没有通过实验验证这几个（吸引）程度”。关于他的整个提议：“我现在仅暗示这一点”，“我手头上有许多我要首先完成的其他事情，因此不能很好地参加”（即 “起诉本调查”）。[10]后来，在 1679 年 1 月 6 日|80 写给牛顿的信中，[13] 胡克向牛顿传达了他的 “假设”...引力与距离中心的倒数成正比，因此速度与引力成反比，因此，开普勒假设对距离的相互作用。”[14] (关于速度的推断是不正确的。) [15]

　　胡克在 1679-1680 年间与牛顿的通信不仅提到了引力随距离增加而下降的平方反比假设，而且在胡克 1679 年 11 月 24 日给牛顿的公开信中，提出了一种 “通过切线将行星的直线运动和朝向中心体的吸引运动合成” 的方法。[16]

1.4 牛顿的工作和主张

　　牛顿在 1686 年 5 月面对胡克对平方反比定律的主张，否认胡克被认为是这个想法的作者。其中一个原因是，牛顿回忆起在胡克 1679 年的信之前，他曾与克里斯托弗·雷恩爵士讨论过这个想法。[17]牛顿还指出并承认其他人以前的研究，[18]包括布礼奥多斯，[6](提出但未证明，来自太阳的吸引力与距离成反比)，和波雷利[7](建议但也没有证明，在对太阳的重力吸引下，平衡会出现离心趋势，从而使行星运动成椭圆形)。D T .怀特塞德描述了博雷利的书对牛顿思想的贡献，他去世时，这本书的副本就在牛顿去世时的图书馆里。[8]

　　牛顿进一步为他的工作辩护说，如果他第一次从胡克那里听说平方反比定律，鉴于他对其准确性的证明，他仍然有一些权利。胡克没有支持这一假设的证据，只能猜测平方反比定律在离中心很远的地方近似有效。牛顿认为，《原理》还处于出版前阶段，有太多先验的理由怀疑平方反比定律的准确性(特别是在吸引区域附近)，以至于 “没有我（牛顿的）的证明，胡克先生还只是一个陌生人，一个明智的哲学家不能相信它是准确的。”[19]

　　这句话主要指的是牛顿发现这个理论有数学证明支持，如果平方反比定律适用于微小的粒子，那么即使是一个大的球对称质量也会吸引其表面以外的质量，即使是靠近它，就好像它自己的质量都集中在它的中心一样。因此，牛顿给出了一个论据，否则就没有理由将平方反比定律应用于大的球形行星质量，就好像它们是微小的粒子一样。[20]此外，牛顿在第 1 本书的命题 43-45[21]和第 3 本书的相关章节中制定了对平方反比定律准确性的敏感测试。他在书中指出，只有当力的定律被计算为距离的平方反比时，行星轨道椭圆的方向才会保持不变，因为行星间摄动造成的影响十分微小。

　　关于早期历史仍然存在的证据，牛顿在 16 世纪 60 年代写的手稿表明，到 1669 年，牛顿本人已经得出了证明，在行星运动的圆形情况下，“努力后退”(后来被称为离心力)与距中心的距离呈平方反比关系。[22]牛顿在 1679-1680 年与胡克通信后，采用了内向力或向心力的用词。根据牛顿学者布鲁斯·布莱肯里奇(J. Bruce Brackenridge)的说法，尽管在离心力和向心力之间的语言变化和观点差异方面做了很多工作，但实际计算和证明无论如何都保持不变。它们还涉及切线位移和径向位移的组合，这是牛顿在 16 世纪 60 年代提出的。胡克在这里给牛顿的观点虽然重要，但只是一个视角，并没有改变分析本质。[23]这一背景表明牛顿有理由否认从胡克定律推导出平方反比定律。

1.5 牛顿的致谢

　　另一方面，牛顿确实在《原理》的所有版本中都承认并致谢，胡克（但不仅限于胡克）已经分别研究了太阳系中的平方反比定律。牛顿在注释中承认雷恩、胡克和哈雷在这方面的研究与第 1 卷中的命题 4 有关。[24]牛顿还向哈雷致谢，他在 1679-1680 年与胡克的通信激发了他对天文问题潜在的兴趣，但根据牛顿的说法，这并不意味着胡克告诉了牛顿任何新的或原创的东西:“然而，我不是因为他对那项事业有所贡献而感激他，只是因为他把我从其他研究中转移到思考这些事情上，而且因为他在写作中的教条主义，就好像他发现了椭圆运动的奥妙，这使我倾向于尝试……”[18]

1.6 现代优先权争议

　　自从牛顿和胡克时代以来，学术讨论也触及了胡克在 1679 年提到的 “复合运动” 是否为牛顿提供了新的和有价值的东西的问题，尽管当时胡克并没有真正提出这一主张。如上所述，牛顿在 16 世纪 60 年代的手稿确实显示了他实际上将切向运动与径向力或力的作用结合起来，例如在他推导圆形情况的平方反比关系时。它们还表明牛顿清楚地表达了线性惯性的概念——为此，他感谢笛卡尔在 1644 年发表的工作(胡克可能就是这样)。[25]牛顿似乎没有从胡克那里学到这些东西。

　　然而，许多作者对牛顿从胡克的思想中学到了什么有更多的看法，一些方面仍然有争议。[5]鉴于胡克的大多数私人文件已经被销毁或消失的事实，真相无法被确定。

　　牛顿在平方反比定律中的作用并不像它有时被描述的那样。他没有声称把它想成一个简单的想法。牛顿所做的是展示平方反比引力定律与太阳系中物体运动的可观测特征有许多必要的数学联系；并且它们之间的联系使得观测证据和数学证明结合起来，有理由相信平方反比定律不仅近似为真，而且完全为真 (达到牛顿时代和大约两个世纪后所能达到的精度，虽然还存在一些尚不能确定的松散点，一些理论的含义尚未充分确定或计算)。[26][27]

　　大约在牛顿于 1727 年去世三十年后，重力研究领域的数学天文学家亚历克西斯·克劳德·克莱罗在回顾胡克发表的文章后写道:“人们不能认为这个想法...胡克的存在削弱了牛顿的荣耀”；而 “胡克的例子” 用来 “表明被瞥见的真理和被展示的真理之间的距离”。[28][29]

2. 现代形式

　　在现代表述中，牛顿万有引力定律规定如下:

表1：

每个点质量都受到沿与两个点相交的线的作用力吸引的每个其他点质量。力与两个质量的乘积成正比，与它们之间的距离的平方成反比:[2]

$ F = G \frac{m_1 m_2}{r^2} $ 其中：

$F$ 是质量之间的力；
$G$ 是重力常数（$6.674 \times 10^{11} \\ \text{N} (\text{米}^2/\text{千克}^2)$）；
$m_1$ 是第一个物体的质量；
$m_2$ 是第二个物体的质量；
$r$ 是质心之间的距离。

图 1

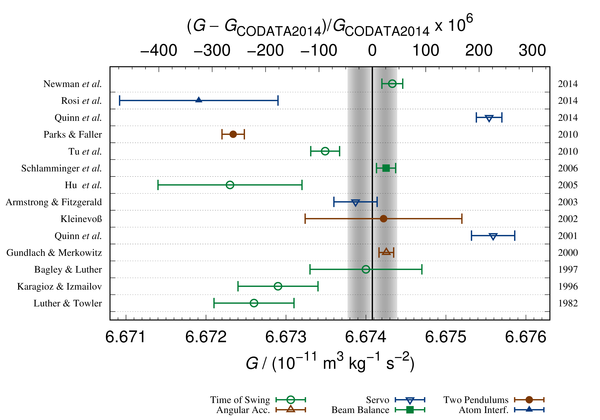
　　国际单位制中,$F$ 用牛顿 $(N)$ 来测量，$m_1$ 和 $m_2$ 以千克 $(kg)$ 为单位，$r$ 单位为米 $(m)$，常数为 G 大约等于 $ 6.674 \times 10^{-11} \text{N} \text{m}^2 \text{kg}^{-2}$。[30] 常数的值 G 是在 1798 年由英国科学家亨利·卡文迪许进行的卡文迪什实验中第一次准确地测出，尽管卡文迪什本人没有计算出 G。[3]该实验也是实验室中对牛顿质量间引力理论的第一次测试。它发生在牛顿原理出版后 111 年，牛顿去世后 71 年，所以牛顿的计算都不能使用 G 的值。相反，他只能计算相对于另一种力的一种力。

图 2：误差图显示了大 g 的实验值。

3. 具有空间范围的物体

图 3：地球上的重力场强度

　　如果所讨论的物体具有空间范围（而不是点质量），则它们之间的重力是通过对构成物体的概念性点质量的贡献求和来计算的。在极限情况下，随着组成点质量 “无限小” 时，这需要在两个物体的范围内对力（矢量形式，见下文）进行积分。

　　通过这种方式，可以证明质量分布呈球对称的物体对外部物体施加了相同的引力，就好像所有物体的质量都集中在它的中心点一样。[2](对于非球对称的物体，这通常是不正确的。)

图 4：地球表面附近的重力场——一个物体向表面加速

　　对于物质的球体内部对称分布的点，牛顿的壳层定理定律可以用来寻找引力。该定理告诉我们质量分布的不同部分如何影响在距质量分布中心 r0 的点处测得的重力：[31]

质量位于半径 $r < r_0$ 的部分在 $r_0$ 处产生的力相同，就好像包围在半径 $r_0$ 的球体内的所有质量都集中在质量分布的中心一样（如上所述）。
质量位于半径 $r> r_0$ 的部分在距中心的距离 $r_0$ 处不施加任何净重力。也就是说，在 $r_0$ 点上，由球体的各个元素施加的各个重力相互抵消

　　因此，在厚度和密度均一的壳体内，空心球内的任何地方都没有净重力加速度。

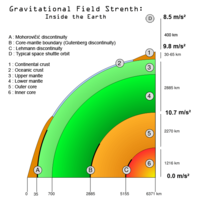
　　此外，在均匀球体内部，重力随着离中心的距离线性增加；由于附加质量而导致的增加是因距中心距离较大而导致减少的 1.5 倍。因此，如果球对称体具有均匀的核和密度小于核密度 2/3 的均匀地幔，那么重力最初在边界之外向外减小，如果球足够大，进一步向外重力再次增加，最终在核/地幔边界处超过重力。地球的重力可能在地核/地幔边界最高。

4. 向量形式

图 5：从宏观角度看地球周围的重力场。

　　牛顿万有引力定律可以写成矢量方程，以说明力的方向及其大小。在该公式中，粗体表示矢量。

　　 $\mathbf{F}{21} = -G \frac{m_1 m_2}{|\mathbf{r}{12}|^2} \hat{\mathbf{r}}_{12}$

　　其中

　　 $\mathbf{F}_{21}$ 是物体 1 施加在物体 2 上的力，

　　 $G$ 是重力常数，

　　 $m_1$ 和 $m_2$ 分别是物体 1 和 2 的质量，

　　 $|\mathbf{r}_{12}| = |\mathbf{r}_2 - \mathbf{r}_1|$ 是物体 1 和物体 2 之间的距离，

　　 $\hat{\mathbf{r}}_{12} \stackrel{\text{def}}{=} \frac{\mathbf{r}_2 - \mathbf{r}_1}{|\mathbf{r}_2 - \mathbf{r}_1|}$ 是从对象 1 到对象 2 的单位矢量。

　　可以看出，方程的矢量形式与前面给出的标量形式相同，除了 $\mathbf{F}$ 现在是一个向量，并且有边乘以适当的单位向量。此外，可以看出 $\mathbf{F}_{12} = -\mathbf{F}_{21}$。

5. 重力场

　　 重力场是一个矢量场，重力场是矢量场，描述了每单位质量在空间中任何给定点上将施加在物体上的重力。它实际上等于该点的重力加速度。

　　它是矢量形式的推广，如果涉及到两个以上的物体(如地球和月球之间的火箭)，它就变得特别有用。对于两个物体(例如，物体 2 是火箭，物体 1 是地球)，我们简单地写 $r$ 代替 $r_{12}$ 和 $m$ 代替 $m_2$ 定义引力场 $g(r)$ 定义为:

\begin{equation} \mathbf{g}(\mathbf{r}) = -G \frac{m_1}{|\mathbf{r}|^2} \hat{\mathbf{r}}~ \end{equation}

　　这样我们就可以得到:

\begin{equation} \mathbf{F}(\mathbf{r}) = m \mathbf{g}(\mathbf{r})~ \end{equation}

　　这个公式取决于引起场的对象。该场有加速度单位；在 SI 中，表示为 $m/s^2$。

　　重力场也是保守的；也就是说，重力从一个位置到另一个位置所做的功与路径无关。这就导致了引力势场的存在 $V(\mathbf{r})$ 使得

\begin{equation} \mathbf{g}(\mathbf{r}) = -\nabla V(\mathbf{r})~ \end{equation}

　　如果 $m_1$ 是点质量或质量分布均匀的球体的质量，力场 $\mathbf{g}(\mathbf{r})$ 球体外部是各向同性的，即仅取决于距离球体的中心距离。在这种情况下

\begin{equation} V(\mathbf{r}) = -G \frac{m_1}{r}~ \end{equation}

　　引力场在对称质量的内部和外部。

　　根据高斯定律，对称体中的场可以通过数学方程找到:

　　 $\partial V \\ \mathbf{g}(\mathbf{r}) \cdot d\mathbf{A} = -4\pi GM_{\text{enc}}$,

　　其中 $\partial V$ 是一个封闭的表面，$M_{\text{enc}}$ 是被表面包围的质量。

　　因此，对于半径为 $R$ 和总质量 $M$，

　　 $\left| \mathbf{g}(\mathbf{r}) \right| = \begin{cases} 0, & \text{if} r < R \\\\ \frac{GM}{r^2}, & \text{if} \ r \geq R \end{cases}$

　　对于半径一致的实心球 R 和总质量 M，

　　 $\left| \mathbf{g}(\mathbf{r}) \right| = \begin{cases} \frac{GMr}{R^3}, & \text{if} r < R \\\\ \frac{GM}{r^2}, & \text{if} r \geq R \end{cases}$

6. 有问题的方面

　　牛顿对重力的描述对于许多实际用途来说足够精确，因此被广泛使用。当无量纲量 $\varphi/c^2$ 和 $(v/c)^2$ 都远远小于一个，其中 $\varphi$ 是重力势，$v$ 被研究物体的速度，$c$ 是光速。例如，牛顿重力提供了地球/太阳系统的精确描述，因为 $\frac{\Phi}{c^2} = \frac{GM_{\text{sun}}}{r_{\text{orbit}} c^2} \sim 10^{-8}, \quad \left(\frac{V_{\text{Earth}}}{c}\right)^2 = \left(\frac{2 \pi r_{\text{orbit}}}{(1 \, \text{yr}) c}\right)^2 \sim 10^{-8}$

　　其中 $r$ 轨道是地球公转轨道的半径。

　　在无量纲参数较大的情况下，则必须用广义相对论来描述这个系统。广义相对论在小势能和低速极限下简化为牛顿引力，因此牛顿引力定律被称为广义相对论的低引力极限。

6.1 对牛顿表达式的理论关注

目前还没有确定重力介体的直接前景。尽管在过去的 50 年中取得了长足的进步，但物理学家尝试确定重力与其他已知基本力之间的关系的尝试尚未解决(参见:万有理论和标准模型)中。牛顿自己也觉得远距离行动是一个一个无法解释的概念，并不令人感到满意 (见下文 “”），但当时他无能为力。
牛顿的万有引力理论要求万有引力是瞬时传递的。考虑到广义相对论发展之前的时空性质的经典假设，重力的显着传播延迟会导致行星和恒星轨道不稳定。

6.2 与牛顿公式相矛盾的观察结果

牛顿的理论并未完全解释行星，尤其是水星行星的近日点的进动，这是在牛顿的生命时期很久之后才发现的。[33]牛顿的计算结果与世纪之间存在 43 弧秒的差异，这仅是由其他行星的引力引力引起的，与观测到的进动之间的差异是由 19 世纪使用先进的望远镜产生的。
通过使用牛顿理论计算得出的重力引力的预测角偏斜仅是天文学家实际观察到的偏角的一半。使用广义相对论进行的计算与天文观测结果更加接近。
在螺旋星系中，恒星绕其中心运行似乎强烈违背牛顿的万有引力定律。但是，天体物理学家在牛顿定律的框架下解释了这种壮观现象，其中存在大量暗物质。

6.3 牛顿的保留意见

　　尽管牛顿能够在他的巨著中阐明他的万有引力定律，但他对他的等式所暗示的 “远距离行动” 这一概念感到非常不自在。1692 年，他在给本特利（Bentley）的第三封信中写道：“一个物体可以通过真空远距离作用于另一个，而无需其他任何介质的干预，通过它们可以相互传递其作用力和力量。对我来说，这是如此荒谬，以至于我认为，任何在哲学问题上有能力思考的人都不可能陷入其中。”

　　用他的话说，他从不 “指派这种力量的原因”。在所有其他情况下，他都使用运动现象来解释作用在人体上的各种力的起源，但是在重力的情况下，他无法通过实验来识别产生重力的运动（尽管他在 1675 年和 1717 年发明了两个机械假设）。而且，他甚至拒绝提供关于这种力量成因的假设，理由是这样做与健全的科学相反。他感叹 “迄今为止，哲学家们一直企图徒劳地寻找自然” 作为引力的源头，因为他 “因许多原因” 确信存在着 “迄今未知的原因”，这是所有 “自然现象” 的基础”。这些基本现象仍在研究中，尽管假说比比皆是，但尚未找到确定的答案。在牛顿的 1713 年第二版《原理》的附录中:“我还不能从现象中发现引力这些特性的原因，我也没有假装没有假说....只要引力确实存在，并按照我解释的规律运行就足够了，它充分解释了天体的所有运动。”[34]

6.4 爱因斯坦的解决方案

　　这些反对意见是由爱因斯坦的广义相对论解释的，在该理论中，引力是弯曲时空的属性，而不是由于物体之间传播的力引起的。在爱因斯坦的理论中，能量和动量使它们附近的时空扭曲，而其他粒子沿由时空几何形状确定的轨迹运动。这样就可以描述与所有可用观测结果一致的光和质量运动。在广义相对论中，重力是由于时空弯曲而产生的虚拟力，这是因为物体自由下落时的重力加速度是由于其世界线是时空的测地线而引起的。

7. 延伸

　　牛顿是第一个在其原理中考虑引力定律扩展表达式的人，包括形式的反立方项 $F = G \frac{m_1 m_2}{r^2} + B \frac{m_1 m_2}{r^3} , B \text{ 是常数}$

　　试图解释月球轨道的运动。拉普拉斯 (大约在 1790 年) 和德科姆比斯 (1913 年) 提出了其他扩展：

　　 $F(r) = k \frac{m_1 m_2}{r^2} \exp\left(-\alpha r\right) \quad (\text{拉普拉斯})$

　　 $F(r) = k \frac{m_1 m_2}{r^2} \left(1 + \frac{\alpha}{r^3}\right) \quad (\text{德科姆比斯})$

　　近年来，利用中子干涉测量法对重力定律中的非平方反比项进行了探索。

8. 万有引力方程的解决方案

　　 $n$ 体问题是一个古老的经典问题[37]，它预测引力相互作用的一组天体的个体运动。从希腊时代开始解决这个问题的动机就是希望了解太阳，行星和可见恒星的运动。在 20 世纪，了解球状星团系统的动力学也成为一个重要的 $n$ 体问题。[38]广义相对论中的 $n$ 体问题很难解决。

　　经典物理问题可以非正式地表述为:给定准稳态轨道特性（瞬时位置、速度和时间)[39] 预测一组天体的相互作用力；从而预测它们未来所有时间的真实轨道运动。[40]

　　两体问题已经完全解决，受限的三体问题也是如此。[41]

9. 参考文献

艾萨克·牛顿:“在[实验中]哲学从现象中推导出特定的命题，然后通过归纳将其一般化。”:《原理》，第 3 卷，斯科尔斯将军，1729 年出版的安德鲁·莫特英译本第 2 卷，第 392 页。.
——命题 75，定理 35:p . 956——I .伯纳德·科恩和安妮·惠特曼，译者:艾萨克·牛顿，《原理》* 科学素养文库·科学元典丛书。在...之前牛顿原理指南作者:伯纳德·科恩。加州大学出版社 1999ISBN 0-520-08816-6 ISBN 0-520-08817-4.
林可唯-卡文迪什实验·洛朗·霍奇斯.
J.L .海尔布隆，17 和 18 世纪的电:早期现代物理学研究(伯克利:加州大学出版社，1979)，180。.
讨论点可以在以下论文中看到:N . Guicciardini，“重新考虑胡克-牛顿关于引力的辩论:最近的结果”，载于《早期科学和医学》，10 (2005)，511-517；Ofer Gal，《天体力学的发明》，载于《早期科学和医学》，10 卷(2005 年)，第 529-534 页；诺恩伯格，“胡克和牛顿对航天动力学和万有引力早期发展的贡献”，载于《早期科学和医学》，10 卷(2005 年)，第 518-528 页。.
^布利尔达斯(伊斯梅尔·布伊拉乌)(1645)，" Astronomia philolaica "，巴黎，1645 年。.
Borelli，G. A .，" theory CAE medieorum Planetarum ex cause physicis deratea "，Florence，1666 ..
D T .怀特塞德，“在原理出现之前:牛顿动力天文学思想的成熟，1664-1684”，《天文学史杂志》，i (1970)，第 5-19 页；尤其是在第 13 页。.
特恩布尔(编辑。)，艾萨克·牛顿的通信，第 2 卷(1676-1687)，(剑桥大学出版社，1960)，在第 431-448 页给出了 1686 年 5 月至 7 月关于胡克主张的哈雷-牛顿通信，特别参见第 431 页。.
胡克 1674 年在《从观测中证明地球运动的尝试》中的陈述可以在在线传真。.
Purrington, Robert D. (2009). The First Professional Scientist: Robert Hooke and the Royal Society of London. Springer. p. 168. ISBN 978-3-0346-0036-1. 第 168 页摘录.
参见柯蒂斯·威尔逊(1989)的第 239 页，“牛顿天文学的成就”，第 13 章(第 233-274 页)，载于 “行星天文学从文艺复兴到天体物理学的兴起:2A:第谷·布拉尼到牛顿”，CUP 1989。.
《1750 年日历(新样式)法案》.
第 309 页，特恩布尔编辑。)，艾萨克·牛顿的通信，第 2 卷(1676-1687)，(剑桥大学出版社，1960)，文件#239。.
参见柯蒂斯·威尔逊(1989)第 244 页。.
第 297 页，特恩布尔编辑。)，艾萨克·牛顿的通信，第 2 卷(1676-1687)，(剑桥大学出版社，1960)，文件#235，1679 年 11 月 24 日。.
第 433 页，特恩布尔编辑。)，艾萨克·牛顿的通信，第 2 卷(1676-1687)，(剑桥大学出版社，1960)，文件#286，1686 年 5 月 27 日。.
特恩布尔出版社(编辑)第 435-440 页。)，艾萨克·牛顿的通信，第 2 卷(1676-1687)，(剑桥大学出版社，1960)，文件#288，1686 年 6 月 20 日。.
第 436 页，通信，第 2 卷，已经被引用。.
命题 70 到 75 在第 1 卷，例如在 1729 年的英文翻译原理,从第 263 页开始。.
命题 43 至 45 在第 1 卷，在 1729 年的英文翻译原理,从第 177 页开始。.
D T .怀特塞德，“从 1664 年到 1686 年‘元首制’的史前史”，《伦敦皇家学会笔记和记录》，45 (1991)，第 11-61 页；尤其是 13-20 岁的时候。.
见布鲁斯·布雷肯里奇，“牛顿动力学的关键:开普勒问题和原理”，(加州大学出版社，1995 年)，特别是在第 20-21 页。.
例如参见 1729 年的英文翻译原理,在第 66 页。.
参见 D T .怀特塞德的第 10 页，“在《原理之前:牛顿动力天文学思想的成熟，1664-1684”，《天文学史杂志》，i (1970)，第 5-19 页。.
例如，参见上面引用的第 1 卷中命题 43-45 和 70-75 的结果。.
另见 G . E .史密斯，在史丹佛哲学百科全书，《牛顿的自然哲学数学原理》。。.
第二段摘录引用并翻译于 W.W .劳斯·鲍尔的《牛顿‘原理’随笔》(伦敦和纽约:麦克米伦，1893 年)，第 69 页。.
克莱罗的原始陈述(法文)可在 “世界体系的渡厄解释和牛顿的壮年兵天体物理学原理的解释”(1759 年)第 6 页导言(第九节)中找到...拿戈卢·德·牛顿的《胡克定律》和[的《胡克定律》:“让距离和距离成为一种趋势，一种趋势”。.
Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006" (PDF). Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP...80..633M. doi:10.1103/RevModPhys.80.633. Archived from the original (PDF) on 2017-10-01. Direct link to value.。.
平衡状态.
Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. New York: W. H.Freeman and Company. ISBN 978-0-7167-0344-0 第 1049 页。.
- 梅克斯·玻恩 (1924)，爱因斯坦的相对论(多佛 1962 年版，第 348 页列出了记录水星、金星和地球近日点进动观测和计算值的表格。).
-现代科学的建构:机制与力学作者:理查德·韦斯特法尔。剑桥大学出版社。1978.
Has, Ioan; Miclaus, Simona; Has, Aurelian (December 2008). "Analysis of a possible correlation between electrical and gravitational forces". Physics Essays. 21 (4): 303–312. doi:10.4006/1.3038751..
Greene, Geoffrey L.; Gudkov, Vladimir (2007). "Neutron interferometric method to provide improved constraints on non-Newtonian gravity at the nanometer scale". Physical Review C. 75 (1): 015501. arXiv:hep-ph/0608346. Bibcode:2007PhRvC..75a5501G. doi:10.1103/PhysRevC.75.015501..
莱马尼斯和米诺斯基:我们对莱马尼斯感兴趣，他首先讨论了一些关于 n——身体问题，特别是柯瓦列夫斯卡娅女士的~1868-1888 年，二十年复变方法，失败；第一节:刚体动力学和数学外弹道(第 1 章，刚体绕不动点的运动（欧拉和泊松方程式)；第二章，数学外弹道)，良好的前体背景 n-身体问题；第 2 节:天体力学(第 1 章，三体问题的均匀化(限制性三体问题)；第二章，在三体问题被俘；第三章，广义 n 体问题)中。.
参见海格和休的参考资料。维基百科的这个页面已经让他们的方法过时了。.
准稳定的载荷是指瞬时角速度和加速度以及平移加速度(9 个变量)产生的瞬时惯性载荷。就像拍了一张照片，它也记录了运动的瞬时位置和特性。相比之下，一个不变的条件是指系统的状态对时间不变；否则，一阶导数和所有高阶导数都为零。.
R.罗森伯格先生指出 n-身体问题类似(参见参考文献):有限粒子系统中的每个粒子都受到来自所有其他粒子的牛顿引力的吸引，而不受其他力的影响。如果给定系统的初始状态，粒子将如何运动？罗森伯格没有像其他人一样意识到有必要确定这些力量第一在运动被确定之前。.
众所周知，用第一积分来表示一般的经典解是不可能的。任意粒子的精确理论解 n 可以通过泰勒级数近似，但是在实践中，这样的无限级数必须被截断，充其量只能给出近似解；一种现在已经过时的方法。此外 n-体问题可以用数值积分来解决，但这些也是近似解；又一次过时了。参见斯维尔·阿塞思的书重力 N 体模拟列于参考文献中。.