贡献者: _Eden_; DTSIo; addis
1. 子列极限与上下极限
我们知道,有许多序列是没有极限的,例如简单的振荡序列 $\{(-1)^n\}$: 它在正负 1 之间无穷多次地跳动,因此它不收敛。但是,它的子序列却可以有极限。
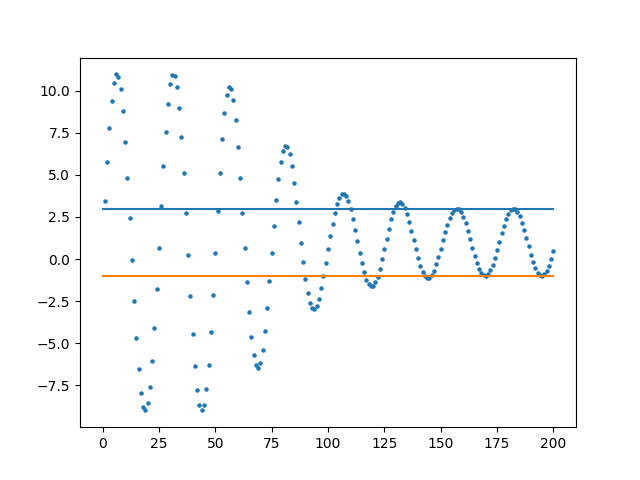
下面我们要介绍的是上下极限的概念,它可以很好地描述序列的 “振荡” 特征。如下图所示,横坐标为 $n$,纵坐标为序列的第 $n$ 个元素 $x_n$。可以发现序列越来越趋向于在橙色线和蓝色线之间振荡。“在无穷远处”,蓝色线 “几乎” 是序列的上界;橙色线 “几乎” 是序列的下界。
图 1:上下极限示意图
为了给出严格的描述,我们需要借助上确界和下确界的语言进行定义。
定义 1 上下极限
设序列 $\{x_n\}$,定义 $l_n=\inf\{x_n,x_{n+1},\cdots\}$,定义 $h_n=\sup\{x_n,x_{n+1},\cdots\}$。也就是说,$l_n$ 是序列从 $n$ 开始的后缀的下确界;$h_n$ 是序列从 $n$ 开始的后缀的上确界。
如果序列有上界,那么 $h_n$ 是良定义的,定义序列的上极限为 $h=\inf\{h_n\}$。
如果序列有下界,那么 $l_n$ 是良定义的,定义序列的下极限为 $l=\sup\{l_n\}$。
记做
\begin{equation}
l= \operatorname {\underline{\lim}}\limits_{n\rightarrow\infty}x_n~,\quad
h= \operatorname {\overline{\lim}}\limits_{n\rightarrow\infty}x_n~.
\end{equation}
图 1 中蓝线代表的是序列的上极限,橙色线代表的是序列的下极限。
习题 1
设序列 $\{x_n\}$ 有界,证明序列的下极限 $l$ 可以用 $\{l_n\}$ 的极限表示;序列的上极限 $h$ 可以用 $\{h_n\}$ 的极限表示:
\begin{equation}
\begin{aligned}
l= \operatorname {\underline{\lim}}\limits_{n\rightarrow\infty}x_n=\lim\limits_{n\rightarrow \infty} l_n~,\\
h= \operatorname {\overline{\lim}}\limits_{n\rightarrow\infty}x_n=\lim\limits_{n\rightarrow \infty} h_n~.
\end{aligned}
\end{equation}
从这个习题我们可以看出,序列的上下极限的含义正是序列在 “无穷远处” 的上界和下界。
2. 上下极限的性质
定理 1
以下三个命题等价:
- $h= \operatorname {\overline{\lim}}\limits_{n\rightarrow\infty}x_n$
- 对任意 $\epsilon>0$,总是存在 $N$,当 $n>N$ 时,总有 $x_n< h+\epsilon$;
对任意 $\epsilon>0$,对任意的 $K$,总是存在 $n>K$,使 $x_{n}>h-\epsilon$。
- 存在子列 $\{x_{n_k}\}$,使得 $\lim\limits_{k\rightarrow\infty}x_{n_k}=h$,并对任何其它收敛子列 $\{x_{n_k}\}$,都有 $\lim\limits_{k\rightarrow\infty}x_{n_k}\leq h$
未完成:最好再补充证明
对于一个实数的子集,将其中的数洒在数轴上,可能会存在这样的点 $x_0$,它周围有无穷多个点 $x$ 在集合中,而且无论把数轴放大多少倍,也是如此。直观上看,集合中的 “点” 聚集在 $x_0$ 周围,所以我们称这样的点为聚点。如果对任意去心邻域 $U_0(x_0,\delta)$,总是存在集合中的某个元素 $x$ 在这个去心邻域中,那么 $x_0$ 就是聚点。下面我们给出形式化的定义:
定义 2 聚点
设 $E$ 是 $\mathbb{R}$ 中的一个子集。若 $x_0 \in \mathbb{R}$($x_0$ 不一定属于 $E$)满足:对任意 $\delta>0$,有 $U_0(x_0,\delta)\cap E\not=\emptyset$,则称 $x_0$ 是 $E$ 的一个聚点。
我们尝试观察序列的上下极限有哪些性质,是否与聚点有关系。从直观上看,如果把序列 $\{x_n\}$ 当作是集合,那么在上极限附近似乎聚集了大量的点,再以上的就都不是聚点了;在下极限附近也似乎聚集了大量的点,再以下的就都不是聚点了。具体地,我们有以下定理:
定理 2 序列极限与聚点
- 若有界序列 $\{x_n\}$ 由互不相同的数组成,则上极限为其最大聚点,下极限为其最小聚点。
- 若 $\{x_{n_k}\}$ 为 $\{x_n\}$ 子列,则有 $ \operatorname {\underline{\lim}}\limits_{n\rightarrow\infty}x_n\leq \operatorname {\underline{\lim}}\limits_{k\rightarrow\infty}x_{n_k}\leq \operatorname {\overline{\lim}}\limits_{k\rightarrow\infty}x_{n_k}\leq \operatorname {\overline{\lim}}\limits_{n\rightarrow\infty}x_{n}$。
- $\lim\limits_{n\rightarrow\infty}x_n=a\Leftrightarrow \operatorname {\underline{\lim}}\limits_{n\rightarrow\infty}x_n= \operatorname {\overline{\lim}}\limits_{n\rightarrow\infty}x_n=a$
习题 2
- 设 $E$ 是 $\mathbb{R}$ 中的一个子集。若 $x$ 是 $E$ 的一个聚点,证明: $\forall \delta>0$,$U(x_0,\delta)\cap E$ 中有无穷多个元素。
- 证明性质 1 和性质 2。
- 利用上下极限证明 $\{\sin n\}$ 发散。
- 序列 $\{x_n\}$ 的上极限为 $h_1$,序列 $\{y_n\}$ 的上极限为 $h_2$,那么序列 $\{x_n+y_n\}$ 的上极限是 $h1+h2$ 吗,$\{x_ny_n\}$ 的上极限是 $h_1\cdot h_2$ 吗?
- 若序列 $\{x_n\}$ 是非负收敛序列,上一问的命题成立吗?
3. 柯西收敛准则
定义 3 柯西序列
设{$x_n$}是一个序列,若对任意 $\epsilon>0$,总是存在 $N$,当 $n,m>N$ 时,有 $\vert x_n-x_m\vert<\epsilon$,则称{$x_n$}是一个柯西序列。
定理 3 柯西收敛准则
序列 {$x_n$} 收敛 $\Leftrightarrow$ {$x_n$} 是一个柯西序列。
定理 4 压缩映像定理
设 $f(x)$ 在 $[a,b]$ 上有定义,$f([a,b])\subset[a,b]$,且存在一个 $(0,1)$ 内的实数 $q$,满足对任意 $x,y\in[a,b]$,都有 $|f(x)-f(y)|\leq q|x-y|$。
那么:存在唯一 $c\in[a,b]$,使 $f(c)=c$。
证明:构造序列 $\{x_n=f(x_{n-1})\}$,用柯西准则证明其收敛。
习题 3
- 写出柯西收敛准则的否命题形式(用肯定的语气写出:怎样的序列不是柯西序列,怎样的序列不是发散的)。
- 试用闭区间套定理证明压缩映像原理。
- 设序列 $\{p_n\}, \{q_n\}$ 满足 $p_{n+1}=p_n+2q_n,\ q_{n+1}=p_n+q_n,\ p_1=q_1=1$,求证 $\left\{\large\frac{p_n}{q_n}\right\}$ 的极限存在,并求其极限。